分布式间歇干扰下基于SMI的GNSS空时自适应处理器性能分析
2023-12-08刘文祥陈飞强
王 解,刘文祥,陈飞强,欧 钢
(1. 国防科技大学 电子科学学院, 湖南 长沙 410073; 2. 国防科技大学 电子对抗学院, 安徽 合肥 230037)
面对日益严重的干扰威胁,抗干扰全球导航卫星系统(global navigation satellite system,GNSS)接收机技术不断得到发展并被应用于不同领域,其中,利用天线阵抗干扰技术被认为最为有效,能够有效抑制多个窄带和宽带干扰信号。在干扰信号连续平稳的条件下,天线阵抗干扰处理表现出较好的干扰抑制性能。然而文献[1-4]的研究工作表明当前GNSS面临的干扰威胁多种多样并在不断地上演着,非平稳和非连续干扰是所面临威胁的一部分。目前很少有文献分析非连续信号对天线阵接收机的影响。文献[5]首先提醒关注非平稳干扰对天线阵卫星接收机的干扰。文献[6]的研究表明天线阵技术不能很好应对非连续的脉冲干扰,必须进一步使用脉冲消隐技术才能应对该干扰场景。这些文献虽然关注了导航频段的非平稳或非连续信号干扰,但是并没有针对非平稳干扰对接收机性能影响展开全面分析。本文针对分布式间歇干扰对阵列GNSS接收机抗干扰处理环节的影响进行精确分析。
分布式间歇干扰是指多个干扰信号在空间上由不同方向入射,在时间上断续存在,其中的单个干扰呈现脉冲干扰特性。分布式间歇干扰之所以对基于递推算法的阵列处理影响较大,是因为信号突变使得滤波器收敛速度下降甚至无法收敛[7],但是对于使用矩阵直接求逆(sample matrix inversion,SMI)算法的抗干扰处理,其收敛速度和采样频率以及长度有关,此时分布式间歇干扰将导致采样协方差矩阵和真实协方差矩阵不匹配。在通信领域也存在由通道间干扰形成的间歇式分布干扰,研究表明干扰将导致基于SMI的阵列处理性能下降[8-10],并给出了优化采样的方法。文献[11-12]分析了在杂波环境下,雷达中空时自适应处理(space-time adaptive processing,STAP)方法的性能,文献[13-15]也分析了在特殊的样本不匹配情况下,阵列雷达处理中信噪比损失概率分布和检测概率。但是GNSS 阵列处理与通信和雷达阵列处理有明显的差别,例如,雷达处理中采样协方差矩阵只能通过相邻距离单元采样数据计算;GNSS应用中采样协方差矩阵的计算则有多种选择方式,这些差别让分布式间歇干扰对GNSS阵列处理的影响明显不同。
在分析分布式间歇干扰的影响时,本文假设干扰的总个数小于阵列的自由度。分布式间歇干扰可由无意干扰或有意干扰形成,而大量无意干扰形成分布式间歇干扰场景比较少见,且有意干扰追求用尽可能少的干扰个数实现最优干扰,因此该假设是符合实际的。并且文章将阵列处理模块作为分析的目标,主要关注卫星信号相关前的干扰抑制性能,将输出功率和信噪比作为性能评估指标。
文章首先介绍分布式间歇干扰的模型并简要介绍GNSS阵列处理的一般流程,然后在分析分布式间歇干扰影响机理和关键因素的基础上,对干扰的影响进行分类评估,在建立分类的不匹配模型之后进行了归纳并给出理论分析结果,并通过数值仿真进行验证,最后提出抗干扰处理设计和优化意见。
1 信号模型和阵列接收机处理流程
1.1 分布式间歇干扰模型
电磁环境中存在大量间歇干扰,在导航频段内,来自塔康导航系统的脉冲信号就属于间歇干扰[6],若间歇干扰由不同方向入射就会构成分布式间歇干扰场景。假设各干扰信号为矩形脉冲调制信号,其载波及带宽和目标卫星信号一致,并假设干扰信号为上升时间和下降时间均为0的理想开关信号。其时域波形描述为:
j(t)=c(t)cos(2πf0t)W(t)
(1)
式中:c(t)为宽带噪声调制信号;f0为载波频率;W(t)为方波,其表达式为
(2)
其中,A为信号的幅值,τ为有效脉冲宽度,T为脉冲周期。
在进行影响分析时,假定干扰相对接收机的空间分布是固定的,在时间上,各干扰信号的到达时间是随机的。给出其时间和空间(到达角:俯仰角θ,方位角φ)的示意图如图 1所示。
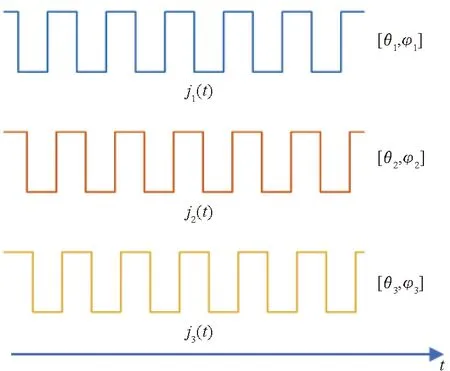
图1 空间分布式间歇干扰信号示意图Fig.1 Schematic diagram of spatially distributed intermittent interferences
1.2 阵列导航接收机抗干扰处理流程
在信号处理流程上,基于数字信号处理的阵列接收机与单天线接收机相比增加了抗干扰处理环节,如图2所示。其信号处理主要包括了射频前端、AD转换、抗干扰处理、通道处理等环节,间歇干扰对上述各环节都会产生一定的影响,文章主要关注间歇干扰对抗干扰处理环节的影响。

图2 阵列接收机信号的处理流程Fig.2 Signal processing flow of array receiver
基于SMI方法的导航接收机STAP抗干扰处理中,利用不同的优化准则求解抗干扰滤波器系数,以最小方差无失真响应(minimum variance distortionless response, MVDR)准则为例,其通过使输出功率为0,并约束卫星信号增益为1,求解滤波器系数:
(3)

假设采样长度为T0时,采样协方差矩阵可以表示为:

(s(t)+sj(t)+n(t))H]dt
(4)

(5)
式中,σ2为噪声功率,Rj表示干扰信号的采样协方差矩阵,Rn为噪声信号协方差矩阵。
2 分布式间歇干扰影响评估
2.1 分布式间歇干扰的影响机理和关键因素
在分布式间歇干扰场景下,干扰信号平稳假设不再成立,使用训练样本计算的协方差矩阵和实际处理信号的协方差矩阵产生了不匹配,造成信噪比损失[13],可表示为:

2.2 干扰影响的分类评估
在分析影响干扰效果的关键因素之后,首先推导了不同场景下训练样本计算协方差矩阵和实际处理信号的真实协方差矩阵不匹配情况,然后总结了间歇干扰下采样协方差矩阵不匹配的几种表现形式,理论分析了不匹配可能造成的信噪比损失,并对出现的概率和影响作了定性分析。
根据上文关键影响因素的分析,下面根据采样长度和处理方式进行具体分析。
2.2.1 采样长度大于闪烁周期
在采样长度大于闪烁周期的情况下,无论是预采样处理还是即时采样处理都有:
(7)
式中:pjn为干扰n的功率;dn为第n个干扰的占空比,为简化分析,假设所有干扰占空比相同;Rjn=pjna(θjn)aH(θjn)。
使用上述采样矩阵进行抗干扰处理后,由于不同时刻天线阵计算协方差矩阵与真实协方差矩阵的不同,因此会在不同时刻产生不同的信噪比损失,而信噪比损失由不同时刻信号的开关决定。
处理信号的真实协方差矩阵为:
(8)
式中,{X} 表示信号为开状态的干扰集合。特殊地,干扰信号全部为开或者全部为关(如图 3中的数据段①和④)。
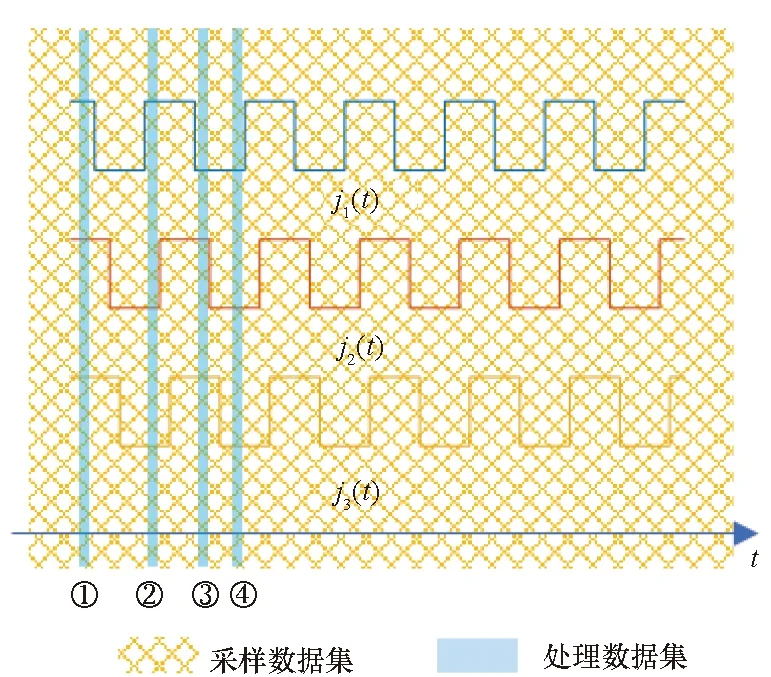
图3 采样长度远大于闪烁周期时采样数据集和处理数据集示意图Fig.3 Sampling data set and processing data set when the sampling length is much larger than the scintillation period
2.2.2 采样长度小于闪烁周期
当采样长度远小于闪烁周期时,需要区分不同采样处理方式,如图4所示。当处理方式是预采样处理时,会出现采样信号和处理信号的不匹配,可分为两种情况。
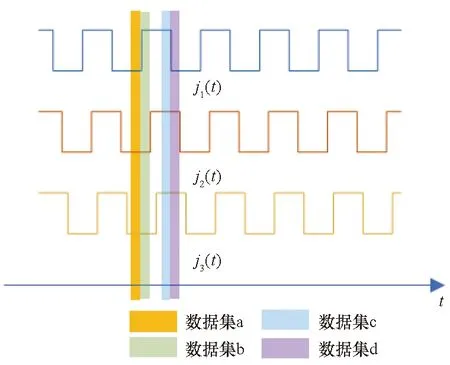
图4 采样长度远小于闪烁周期时采样数据集和处理数据集示意图Fig.4 Sampling data set and processing data set when the sampling length is much less than the scintillation period
一种不匹配是采样信号不包含处理数据中的一个或者几个干扰信号,导致无法抑制未被采样的干扰信号(如图 4所示,若使用数据集a计算的结果处理数据集b,则干扰1无法被抑制),此时采样信号计算协方差矩阵为:
(9)
处理信号的真实协方差矩阵为:
(10)
式中,{Y}表示处理信号中未被采样的干扰信号。
另一种不匹配是采样信号中存在某个或某些干扰信号,处理信号中没有相应的干扰信号(如图4所示,若使用数据集c计算的协方差矩阵的结果处理数据集d,则处理数据中不包含干扰2),此时采样信号计算协方差矩阵为:
式中,{Z}表示被采样但处理信号中不包含的干扰信号。 处理信号的真实协方差矩阵为:
两种不匹配的情况都会产生信噪比损失,发生的频率为各干扰源闪烁频率之和。
使用即时采样时,只有在处理数据段中包含干扰信号跳变过程才会造成协方差矩阵不匹配,在处理该数据段时采样信号为:
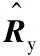
dppjya(θjy)aH(θjy)
(13)
式中,下标jy表示采样集中包含跳变的干扰,dp为被采样长度占整个闪烁周期的比例。若闪烁周期很小,则在采样长度远小于闪烁周期情况下对信号接收和处理的影响几乎可以忽略不计。
通过以上梳理,全面分析了分布式间歇干扰导致的采样数据计算协方差矩阵和处理信号真实协方差矩阵的不匹配情况。根据分析的结果,在进行干扰影响的评估时,区分采样长度和间歇干扰的闪烁周期对比的两种情况。若采样长度远大于干扰闪烁周期,则计算闪烁周期内信号处理的平均信噪比损失;若采样长度远小于干扰闪烁周期,则分别计算不同情况的信噪比损失以及发生的频率。表1总结了几种不匹配情况和影响评估方法。
进一步,可将分布式间歇干扰造成的计算协方差矩阵和处理信号的真实协方差矩阵的不匹配情况归纳为对干扰信号采样不充分、漏采样和过采样,漏采样是采样不充分的特殊情况。
采样不充分时,采样信号和被处理信号的协方差矩阵的关系为:
(14)
式中:{Y} 表示未被充分采样的干扰信号;rjn表示信号采样计算功率和实际功率的比值,rjn=0是表示该信号完全未被采样,属于漏采样。表1中第4,5种情况均属于采样不充分,其中第5种情况下rjn=0,属于漏采样。

表1 协方差矩阵不匹配情况分类及影响评估方法
过采样时,采样信号和实际信号的协方差矩阵的关系为:
(15)
式中:{Z} 表示过采样的干扰信号;特殊地,rjn=1表示采样数据段内干扰信号始终存在,但处理数据段没有该干扰信号,称之为完全过采样。表1第3,6种情况属于过采样。
表1中的第1,2种情况下,由于采样长度远大于闪烁周期,一个采样长度内所有干扰信号都被采样,但是闪烁干扰占空比不为1,导致采样协方差矩阵不能反映真实瞬时功率,因此在干扰信号开关的不同时刻,其协方差矩阵不匹配既有采样不充分也有过采样。
尽管上文对分布式间歇干扰产生的协方差矩阵不匹配进行了分类和精确推导,但仍然不能得出干扰对信噪比产生的损失情况,接下来通过理论推导了各类情况下自适应处理器的性能,并通过设置典型场景,利用数值和仿真精确评估间歇干扰的影响。
3 自适应处理器性能理论分析
第一类情况:采样不充分。协方差矩阵的不匹配表示为:
(16)
式中,q是被部分采样的干扰信号Q的单位导向矢量,k1表示信号漏采样导致的功率损失大小。
由于干扰信号Q已经被部分采样,因此有:
(17)
(18)
其中,k0表示采样计算所得的干扰信号Q的功率,Rx表示除干扰信号Q之外其他干扰信号和噪声信号的协方差矩阵。
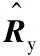
(19)

(20)
显然干扰信号Q的导向矢量q属于干扰子空间,因此,
qHen=0n>P
(21)
根据矩阵求逆引理和式(20)、式(21)得
(22)
式(22)代入式(6)可知在第一类情况下ρa1=1,信噪比基本无损失。
第二类情况: 漏采样。协方差矩阵的不匹配表示为:
(23)
式中,v是完全未被采样的干扰信号V的单位导向矢量,k2表示干扰信号V的功率。
由于干扰信号V完全未被采样,因此,式(22)在该情况下不成立。此时被漏采样的干扰方向未被置零,会导致处理后的输出中包含该干扰信号,信噪比损失ρa2取决于干扰信号导向矢量、功率等因素。
第三类情况: 过采样。协方差矩阵的不匹配表示为:
(24)

对照表1,当采样长度远大于闪烁周期时,不同时刻干扰信号既有采样不充分又有过采样,通过上述推导可知该情况下信噪比基本无损失;当采样长度远小于闪烁周期且即时采样处理时,存在过采样和采样不充分,此时信噪比也基本无损失;当采样长度远小于闪烁周期且预采样处理时,若采样长度结束后处理信号段存在干扰信号关,则出现干扰信号过采样,此时信噪比基本无损失,但是若采样长度结束后处理信号段存在干扰信号开,则出现干扰信号完全未被采样,此时会有明显的信噪比损失。
综上,通过分类、归纳和理论分析表明闪烁干扰导致的采样计算协方差矩阵和真实协方差不匹配只有在一种情况下才会造成明显的信噪比损失,即抗干扰处理器采样长度远小于闪烁周期并使用预采样处理,在采样结束后处理信号段存在干扰信号开时发生,处理该数据段时干扰信号不能完全被抑制。该情况出现的频率为干扰信号闪烁频率之和,此时信噪比损失与干扰信号导向矢量、功率、干扰分布等因素相关,下文将通过数值仿真进行定性和定量分析。
4 数值分析和仿真验证
文章分析时使用四阵元中心圆阵抗干扰接收机,抗干扰处理过程中时域抽头为10个,采样率为40 MHz。设置3个均为宽带脉冲调制的干扰信号,周期为500 μs,占空比为50%,干扰到达角分别为[1°,30°]、[5°,60°]和[10°,120°],干扰功率为-68 dBm,卫星信号功率为-128 dBm,噪声功率为-100 dBm,各脉冲上升沿到达时间不同,如图 1所示。
在以上设置的基础上,首先通过数值分析第3节中不同情况下的信噪比损失。
第一类情况:以图3中的数据段①为例,此时3个干扰信号状态全为开,采样长度远大于脉冲信号周期,干扰信号功率被平均,协方差矩阵不匹配体现为3个干扰信号采样不充分。此时不同方向的信噪比损失如图 5所示。结果表明此时信噪比损失小于0.5 dB,证明ρa1≈1 ,与理论分析结果一致。

图5 采样不充分时的不同方向信噪比损失Fig.5 Loss of signal-to-noise ratio in different directions with insufficient sampling
第二类情况:以图4中数据集a和数据集b为例,使用预采样处理,数据集b中的干扰1漏采样。此时不同方向的信噪比损失如图 6所示,干扰1未被抑制导致在部分方向上信噪比损失达到25 dB以上,验证了理论分析的结果。

图6 漏采样时不同方向的信噪比损失Fig.6 Loss of signal-to-noise ratio in different directions with missed sampling
第三类情况:场景1,以图 3中的数据集④为例,干扰信号为关状态,采样矩阵中则包含3个干扰信号,不同方向的信噪比损失如图7所示,此时,在3个干扰的方向信噪比有明显损失,但是在其他方向损失5 dB左右;场景2,若以图4中数据集c和数据集d为例,数据集c作为采样数据包含干扰1,数据集d作为处理数据不包含干扰1,不同方向的信噪比损失如图 8所示,此时,同样只有在干扰1的方向信噪比有明显损失,其他方向损失较小。以上均为完全过采样(处理信号中完全不包括干扰信号),非完全过采样的情况和采样不充分的情况类似,信噪比基本无损失。

图7 过采样时不同方向信噪比损失(场景1)Fig.7 Loss of signal-to-noise ratio in different directions with redundant sampling(scenario 1)
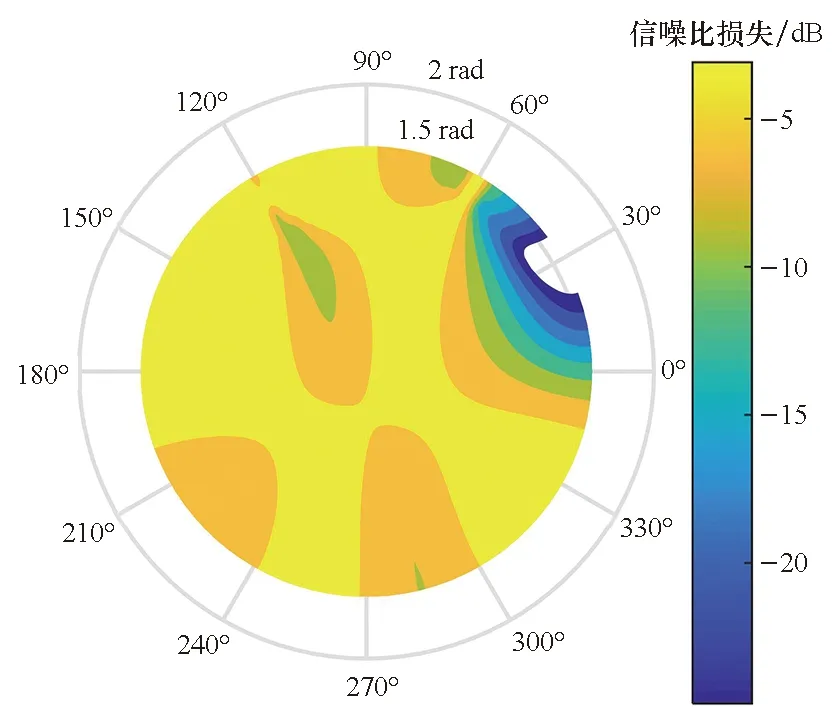
图8 过采样时不同方向信噪比损失(场景2)Fig.8 Loss of signal-to-noise ratio in different directions with redundant sampling(scenario 2)
以上数值分析的结果和理论分析的结果一致,只有在漏采样时,信噪比有较大的损失,同时在完全过采样时,干扰信号来向的信噪比损失较大,这是由于该方向的卫星信号也被抑制。用抗干扰处理仿真系统也可验证上述结论,在上述参数设置的基础上,设置卫星信号的来向为[80°,220°],仿真时长20 ms。进行不同采样长度和采样方式下的仿真处理,包括采样长度为1 ms的即时处理和预处理,采样长度为100 μs的即时处理和预处理。不同设置下的抗干扰处理后输出功率和卫星信号捕获处理相关积分结果如图9~12所示。
根据图9和图10的仿真结果可知,当采样长度为1 ms时,不论是预采样处理还是即时采样处理都能较好抑制干扰,能够完成卫星信号捕获。

(a) 抗干扰处理后输出功率(a) Output power after anti-jamming processing
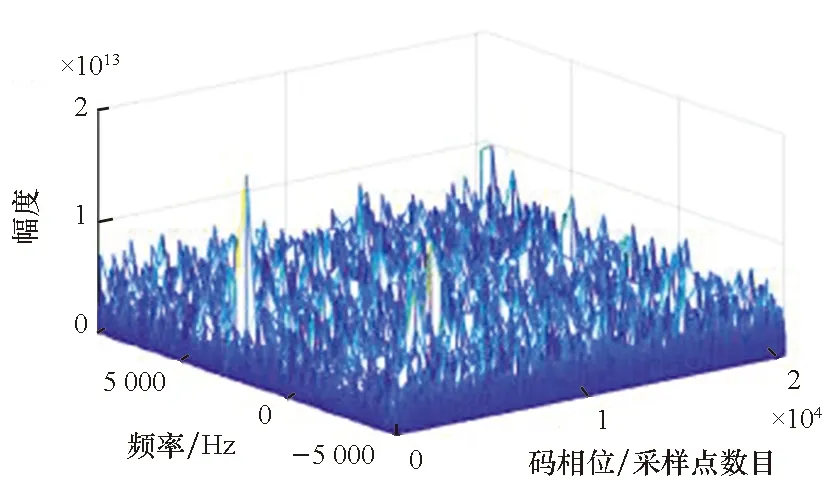
(b) 相关积分输出(b) Output of correlation integral图9 采样长度为1 ms的即时采样处理结果Fig.9 Results of immediate sampling processing with 1 ms sampling length
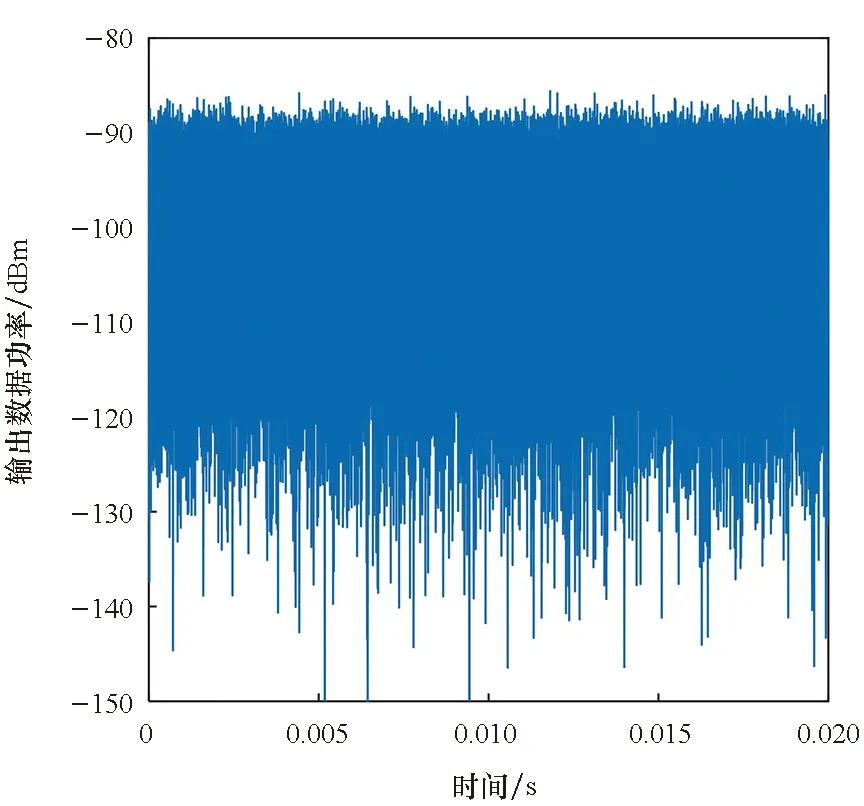
(a) 抗干扰处理后输出功率(a) Output power after anti-jamming processing
(b) 相关积分输出(b) Output of correlation integral图10 采样长度为1 ms的预采样处理结果Fig.10 Results of pre-sampling processing with 1 ms sampling length
在采样长度为100 μs时,即时采样处理也能够很好地抑制干扰并取得很好的捕获结果(如图11所示)。但是在预采样处理时,由于有漏采样出现导致漏采样干扰不能被抑制,抗干扰性能急剧下降,导致信号捕获处理不成功(如图12所示)。上述仿真结果与理论分析的结果一致。
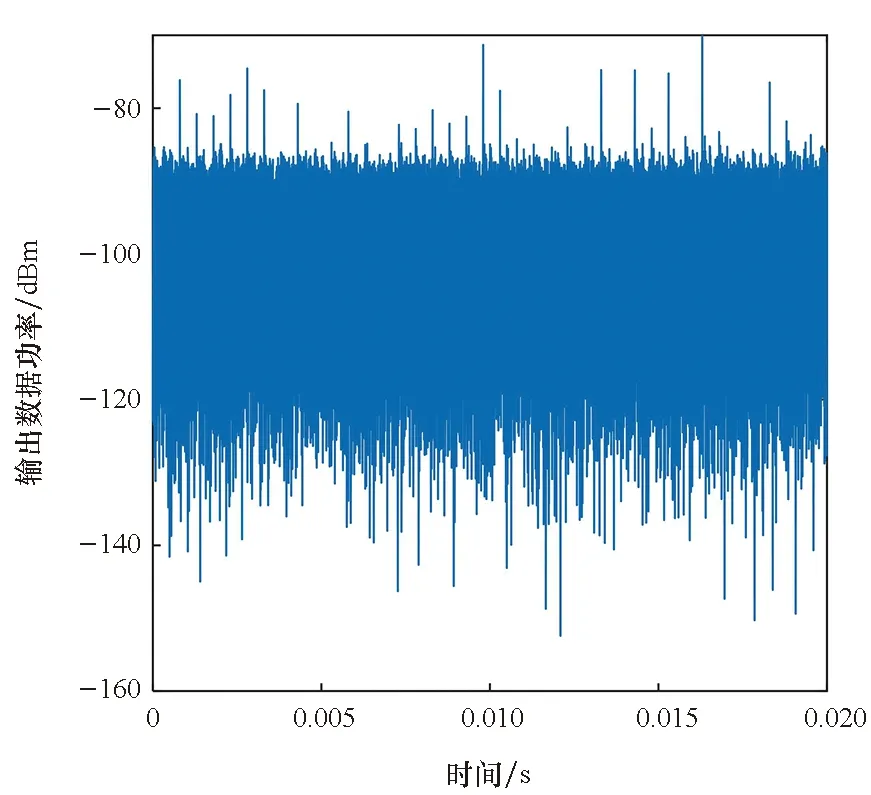
(a) 抗干扰处理后输出功率(a) Output power after anti-jamming processing
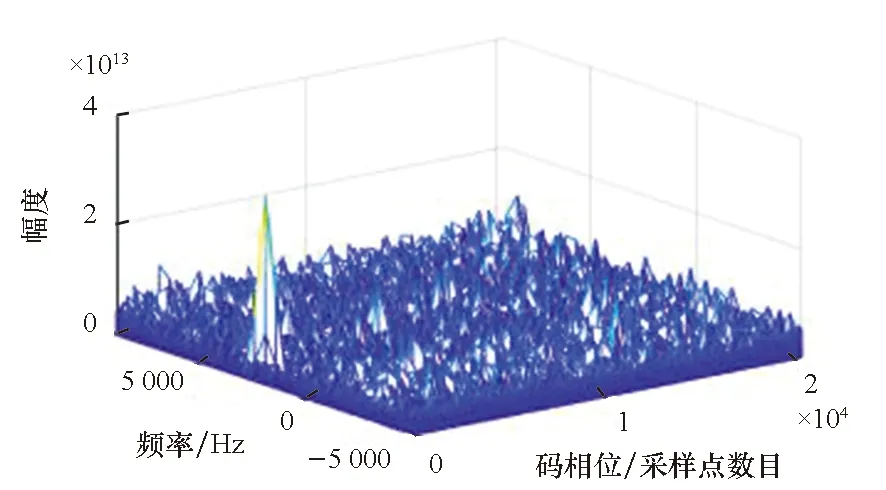
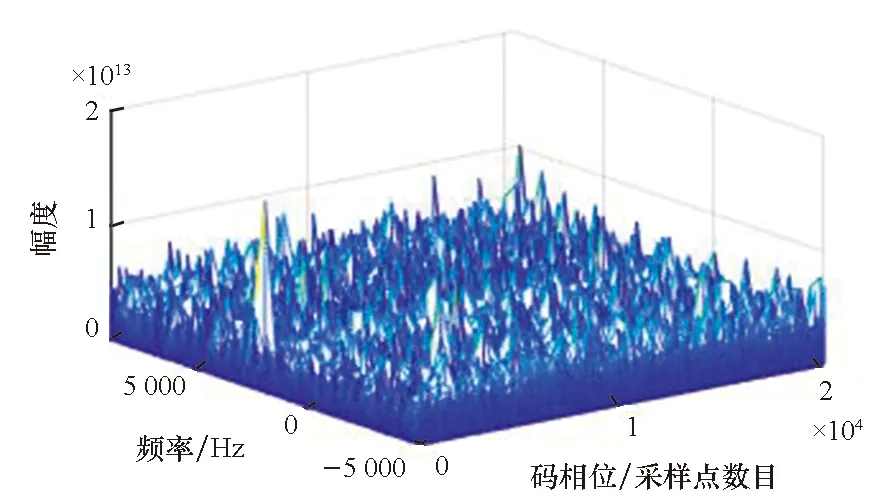
(b) 相关积分输出(b) Output of correlation integral图11 采样长度为100 μs的即时采样处理结果Fig.11 Results of immediate sampling processing with 100 μs sampling length

(a) 抗干扰处理后输出功率(a) Output power after anti-jamming processing

(b) 相关积分输出(b) Output of correlation integral图12 采样长度为100 μs的预采样处理结果Fig.12 Results of pre-sampling processing with 100 μs sampling length
5 讨论
通过数值和仿真分析较好地验证了分类分析、归纳、理论推导的准确性,分布式间歇干扰对基于SMI的抗干扰处理的干扰抑制性能需要区分不同的处理方式和采样长度。只有当采样长度小于闪烁周期且使用预采样处理时,面对分布式间歇干扰,抗干扰处理器性能才会明显下降。从抗干扰角度看,在干扰闪烁周期不确定的情况下如何选择最优的抗干扰处理方法尤为重要[16-17]。
若选择较长的采样长度,则需要使用预采样处理的方式,因为此时若选择即时采样处理则会导致较大的处理延迟,更重要的是所需要的存储空间会大大增加。采用预采样处理的风险在于不能保证采用长度大于闪烁周期,避免漏采样,特别是不同干扰闪烁周期不一致的情况下。且在高动态情况下长采样长度还会导致干扰在空间扩展,消耗空间自由度,降低抗干扰性能。一种改善方法是先估计干扰闪烁周期再自适应调整采样长度。
在不能确定闪烁周期的情况下,选择小的采样长度并且使用即时采样处理方法可以获得较好的抗干扰效果。从理论上来说,在假设信号平稳的前提下,采样协方差矩阵的计算样本点数大于2M-3 就可以使协方差矩阵不匹配造成的信噪比损失小于3 dB,其中M表示协方差矩阵维数。但是即时采样处理会带来信号处理的延迟,并且需要额外的内存来预存采样信号,在接收机对处理延迟不敏感应用中可以采用即时采样处理。若脉冲干扰导致信号平稳的假设不成立,采样协方差矩阵计算样本数与信噪比损失之间的关系将发生变化[18],最小计算样本数需要增加。
综上,面对分布式间歇干扰,采样长度和处理方式有两种选择:一是使用预采样处理提高采样长度;二是使用即时采样处理且尽量小的采样长度。但是这种选择在仅评估干扰抑制能力时是较好的选择,如果考虑相关后的性能,则需要进行进一步的评估,因为面对干扰信号的闪烁,最优权值不断变化,会导致不同的信号失真,造成负面的影响,这些影响如何需要进一步的分析评估[19]。因此,在改善参数设置的基础上,如何结合其他的抗干扰方法消除闪烁干扰仍有待研究。
6 结论
文章全面精确分析了在不同情况下,基于SMI的STAP抗干扰面对分布式间歇干扰的抑制性能,将分布式间歇干扰造成的协方差矩阵不匹配归纳分类,理论分析表明在采样长度小于闪烁周期且使用预采样处理方法时,会出现漏采样,干扰抑制性能会急剧下降。漏采样出现的频率为各干扰闪烁频率之和,数值和仿真分析验证了理论分析的结果,在此基础上讨论了面对分布闪烁干扰如何设置抗干扰参数,以及可能面临的挑战,为应对分布式间歇干扰提供了重要参考。
