裂项相消法求和的类型及求解策略

谢新华

(福建省莆田第二中学,福建 莆田 351131)

1 通项公式为型

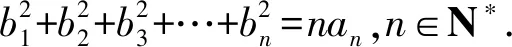
(1)求数列{an}和{bn}的通项公式;

(2)若数列{cn}满足,cn·(bn+bn+1)=6,n∈N*.求数列{cn}的前n项和Tn.

解析(1){an}是等差数列,且满足a1=1,a2,a3+1,a4+6三个数成等比数列.

所以(a3+1)2=a2·(a4+6).

整理,得(1+2d+1)2=(1+d)(1+3d+6).

所以4(d+1)2=(1+d)·(3d+7).

易知d>0,所以4d+4=3d+7,即d=3.

所以an=3n-2.

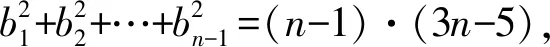
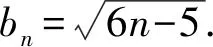
2 通项公式为型

例2在递增等差数列{an}中,a2+a4=8,a1,a3,a7成等比数列.

(1)求数列{an}的通项公式﹔

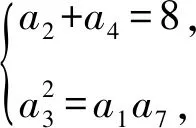
所以an=2+(n-1)×1=n+1.

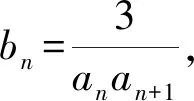
3 通项公式为型

例3记Sn为数列{an}的前n项和,且a1=2,2Sn=(n+1)an.

(1)求Sn;

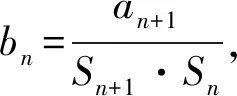
解析(1)由2Sn=(n+1)an,得

2Sn=(n+1)(Sn-Sn-1)(n≥2,n∈N*).

整理,得(n-1)Sn=(n+1)Sn-1.

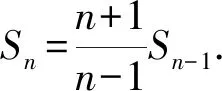
因为S1=a1=2,所以S1也满足Sn=n(n+1).

所以Sn=n(n+1)(n∈N*).

4 通项公式为型

(1)求数列{an},{bn}的通项公式;

解析(1)由于an+1-an=n+1,则

当n=1时,b1=a1=1;

解得Sn=n2,n=1时,b1=1=S1也满足.

所以Sn=n2,

当n≥2时,bn=Sn-Sn-1=2n-1,b1=1符合此式,即bn=2n-1.

c1+c2+…+cn

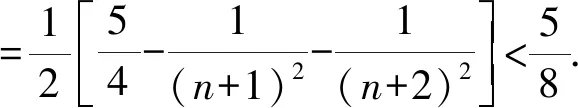
5 通项公式为型

例5已知等比数列{an},其前n项和为Sn,若a1=λ,an+1=λSn+2,λ∈R,n∈N*.

(1)求λ的值;

解析(1)由an+1=λSn+2,an=λSn-1+2(n≥2),两式相减,得

an+1-an=λan.

所以an+1=(λ+1)an(n≥2).

所以{an}是等比数列且a1=λ,a2=λ2+2.

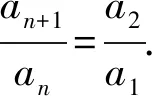
(2){an}是以a1=2为首项,3为公比的等比数列,所以an=2·3n-1.

则b1+b2+…+bn

所以3n>1 011,解得n≥7.

所以满足题意的最小自然数n为7.

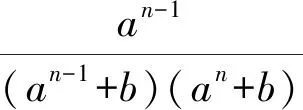
6 通项公式为型

例6已知数列{an}满足:

(1)求数列{an}的通项公式;

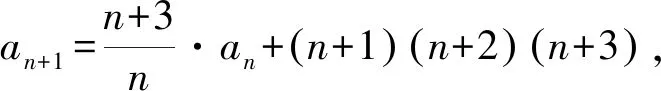
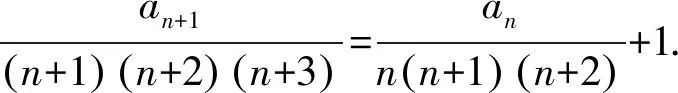
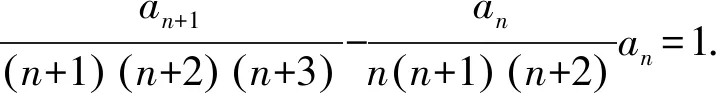
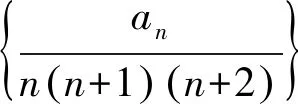
所以an=n(n+1)(n+2)(n+3).

(2)由(1)知

an=n(n+1)(n+2)(n+3).