自适应蒙特卡洛法评定全站仪测距不确定度

2023-12-07仇跃鑫朱进王瑛辉

计测技术 2023年5期

仇跃鑫，朱进，王瑛辉*

（1.浙江省计量科学研究院，浙江杭州 310018；2.浙江省数字精密测量技术研究重点实验室，浙江杭州 310018）

0 引言

全站仪被广泛应用于精密测量、机械制造和大地测量领域，本质是由一个经纬仪和一个电子测距仪共同组成，这二者的精度直接决定了全站仪的精度。全站仪的角度测量系统通常在实验室内校准［1］，测距则需要在野外基线场进行校准，由于野外环境不可控和气象条件波动剧烈［2］，因此通过评定测量不确定度来判断测量结果的可靠程度具有重要意义。

Lauryna Šiaudinyte 使用平面角校准方法对全站仪的竖直角度测量系统进行不确定度评定［3］，并使用测量不确定度表示指南（Guide to the Expression of Uncertainty in Measurement，GUM）对全站仪竖直角度校准的三角法进行了不确定度评定［4］。José L.García-Balboa 使用GUM 对全站仪对中的不确定度进行了评定［5］。范春艳针对GUM 评定测量不确定度时存在的问题，使用蒙特卡洛法（Monte Carlo Method，MCM）对全站仪空间测量不确定度进行评定，着重分析样本数量对仿真效率和准确性的影响［6］。刘胜林使用GUM 对全站仪（测距仪）测尺频率和周期误差振幅的测量不确定度进行评定［7-8］。江洪波使用GUM 对全站仪测距综合标准差的测量不确定度评定和使用全站仪进行短基线测量的精度评定［9-10］。时振伟对全站仪加、乘常数检定精度的影响因素及对策进行了分析［11］。

上述研究内容主要针对全站仪的竖直角测量系统进行测量不确定度评定或者针对测距不确定度来源中的部分误差源进行不确定度评定，没有针对全站仪测距不确定度进行综合分析。

相比于使用GUM 评定测量不确定度，MCM 更适用于解决模型非线性和输入量强相关的问题［12-15］，随着样本数量的增加，MCM 的输出量也会更加精确，但相应地也需要更多的计算时间，自适应蒙特卡洛法（Adaptive Monte Carlo Method，AMCM）是在MCM 的基础上通过输出量达到统计意义上的稳定来平衡输出量的准确度和样本计算时间的矛盾［16-18］。

综上所述，本文根据全站仪测距原理，分析全站仪测距过程中的不确定度来源，建立不确定度评定模型，基于AMCM 进行测距不确定度评定，并与GUM 评定的测量不确定度进行比较，相互验证了二者的可靠程度。

1 不确定度评定模型

全站仪在测量基线边的标准长度Di0时，测量结果D的计算公式为［19］

式中：Di0为基线溯源值，Di为经过频率、气象、倾斜等修正后的观测值，Kc为仪器和棱镜的组合常数，R为仪器乘常数。

对全站仪测距进行测量不确定度分析，其主要误差源包括：标准基线的测量误差、基线漂移、全站仪安装误差、棱镜安装误差、环境参数变化误差、全站仪量化误差、频率漂移、测距倾斜修正误差和随机测量误差。从而得到基于自适应蒙特卡洛法的全站仪测距不确定度评定模型为

式中：ΔD0为基线参考值引入的标准长度ΔDi0变化量；ets为全站仪安装误差引入的测距变化量；ep为棱镜安装误差引入的测距变化量；ΔDenv为环境参数变化引入的测距变化量；σK为仪器和棱镜的组合常数测量随机误差引入的Kc变化量，ΔDe为量化误差引入的测距变化量，ΔDf为频率漂移引入的测距变化量，ΔDtc为倾斜修正引入的测距变化量，σ为随机测量误差引入的Di变化量。

1）基线参考值引入的测量不确定度分量

基线参考值引入的测量不确定度主要来源于基线边标准长度的测量不确定度和基线间的距离漂移。基线边标准长度的扩展测量不确定度为1 mm/km（k= 2），故基线边标准长度的测量不确定度引入的测距变化量ΔDref服从正态分布N（0，0.5 mm/km）。基线间距离漂移引入的测距变化量ΔDdrf通过基线稳定性指标表征，基线稳定性指标优于1.4 mm/km（k= 2），故ΔDdrf服从正态分布N（0，0.7 mm/km）。故由基线参考值引入的标准长度变化量ΔD0计算公式为

2）安装误差引入的测量不确定度分量

全站仪安装误差包括：定位杆偏心、基座偏心和仪器整平误差［20］。全站仪定位杆安装时配合间隙导致的偏心优于0.01 mm，认为全站仪定位杆偏心引入的测距变化量ets1在0.005 mm 的区间半宽内服从正态分布N（0，0.005 mm）。全站仪基座对中时配合间隙导致的偏心优于0.14 mm，认为全站仪基座偏心引入的测距变化量ets2在0.07 mm 的区间半宽内服从正态分布N（0，0.07 mm）。全站仪竖轴未完全垂直于水平面时产生的仪器整平误差优于0.01 mm，认为仪器整平误差引入的测距变化量ets3在0.005 mm的区间半宽内服从正态分布N（0，0.005 mm）。故全站仪安装误差引入的测距变化量ets计算公式为

棱镜安装误差包括：定位杆偏心和仪器整平误差。棱镜定位杆的偏心优于0.01 mm，认为定位杆偏心引入的测距变化量ep1在0.005 mm 的区间半宽内服从正态分布N（0，0.005 mm）。棱镜的整平误差优于0.03 mm，认为仪器整平误差引入的测距变化量ep2在0.015 mm 的区间半宽内服从正态分布N（0，0.015 mm）。故棱镜安装误差引入的测距变化量ep为

3）环境参数引入的测量不确定度分量

环境参数变化引入的测量不确定度表现为温度、湿度和气压的变化导致空气折射率发生变化，使光波在大气中的传播速度发生变化，从而影响全站仪测距结果。由气象修正公式可知温度每变化±1 ℃，大气改正数变化±1 mm/km；气压每变化±3.3 hPa，大气改正数变化±1 mm/km；湿度每变化±60% RH，大气改正数变化±0.5 mm/km。仪器和棱镜的组合常数在实验室内进行测量，两次测量期间的环境温度的变化值小于0.2 ℃，且最长测量距离为18 m，因此环境参数变化引入的测量不确定度极小，忽略不计。

在乘常数标定和实际测量过程中环境温度变化不超过±1 ℃，气压变化不超过±1 hPa，湿度变化不超过±10% RH，故由温度变化引入的测距变化量ΔDt优于±1 mm/km，并在1 mm/km 的区间半宽内服从均匀分布；由湿度变化引入的测距变化量ΔDh优于±0.08 mm/km，并在0.08 mm/km 的区间半宽内服从均匀分布；由气压变化引入的测距变化量ΔDp优于±0.3 mm/km，并在0.3 mm/km的区间半宽服从均匀分布。故由环境参数变化引入的测距变化量ΔDenv为

4）仪器参数引入的测量不确定度

全站仪参数变化引入的测量误差包括量化误差和频率漂移的影响。TC2003 型全站仪的分辨力为0.1 mm，认为量化误差引入的测距变化量ΔDe在0.05 mm的区间半宽内服从均匀分布。仪器标称频率为50 MHz，在开机30 min 后的测距精测频率变化量不超过±5 Hz，由频率漂移引入的测距变化量ΔDf不大于±0.1 mm/km，认为ΔDf在0.1 mm/km的区间半宽内服从均匀分布。

距离测量值倾斜修正引入的测量误差包括标准长度基线场各观测墩之间的高度误差和仪器安装的高度误差影响。各观测墩之间的高度误差不超过2 cm，测量使用的合作目标是徕卡专用精密棱镜组，棱镜中心高与仪器高之差可以忽略不计。按测量的最短距离为48 m 来计算，由其引入的倾斜修正误差ΔDtc不超过±0.09 mm/km，并服从均匀分布。

5）仪器随机测量误差引入的测量不确定度

测量过程中的仪器随机测量误差引入的测量误差中的乘常数随机测量误差通过全站仪观测值的重复性指标给出，通过实验评定得到全站仪的测量重复性σ优于0.16 mm。认为σ服从正态分布N（0，0.16 mm）。

仪器和棱镜的组合常数在室内短基线上单独进行校准，并用于补偿全站仪测量基线边标准长度时的观测值，因此仪器和棱镜的组合常数的随机测量误差σK通过该常数测量过程中的测量重复性指标给出，测量重复性优于0.25 mm，故认为σK服从正态分布N（0，0.25 mm）。

综上所述，将各项误差源汇总如表1所示。

表1 误差源汇总表Tab.1 Summary of error sources

2 测量不确定度评定

2.1 自适应蒙特卡洛法

AMCM 对输入量按相应的概率密度函数进行离散抽样，通过测量不确定度评定模型传递输入量分布和计算得到输出量，进一步获得输出量的最佳估计值、标准不确定度度和包含区间。使用AMCM 评定全站仪测距测量不确定度的试验过程如图1所示。

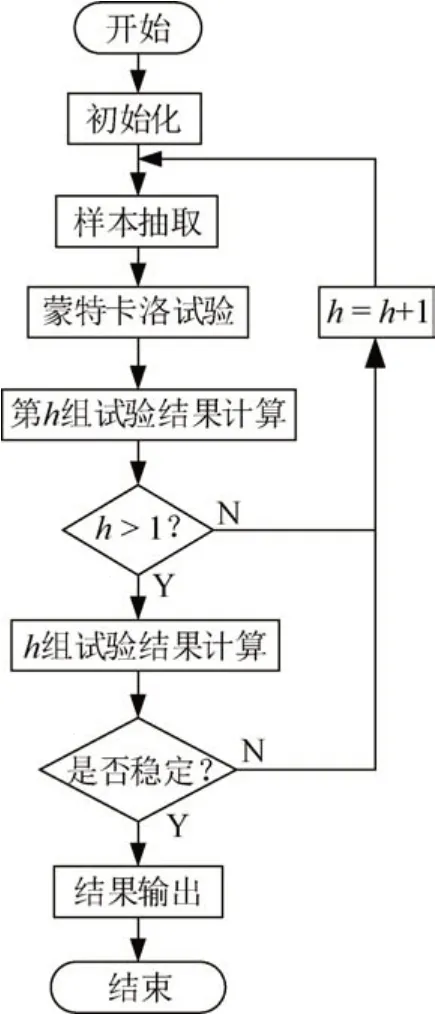
图1 AMCM评定测量不确定度程序流程图Fig.1 Flowchart of measurement uncertainty evaluation by AMCM

1）初始化：包括设置单组试验样本数量M、数值容差δ和试验次数h= 1。M通过式（7）进行设置

式中：J为大于或等于100 /（1-p）的最小整数，当p取99.9%时，J= 105，即单组试验样本数量M= 105。

数值容差δ与全站仪标准测量不确定度的有效位数相关，将全站仪的标准测量不确定度表示为c× 10l，即可通过式（8）得到δ。

2）样本抽取：根据各输入量的概率分布情况抽取M个样本数据。

3）蒙特卡洛试验：抽取的样本根据不确定度评定模型进行计算，并输出当前试验组数据。

4）第h组试验结果计算：包括输出量估计值、标准测量不确定度和概率p的包含区间的左右端点。

5）h组试验结果计算：包括输出量估计值、标准测量不确定度和概率p的包含区间的左右端点的平均值的标准偏差。

6）稳定性判断：判断输出量估计值、标准测量不确定度和概率p的包含区间的左右端点的平均值的标准偏差是否小于数值容差δ，若不成立则继续进行h+ 1组试验。

7）结果输出：使用h×M个模型输出值计算得到输出量估计值、标准测量不确定度和概率p的包含区间。

由于MCM 所需样本数量M的大小与输出量的概率密度函数和包含概率相关，M= 106通常会为输出量提供95%的包含区间，但由于MCM 缺少对结果的验证，无法保证样本数量是否足够，所以一般需要大量样本数据进行模拟保证输出量准确，样本数据计算时间随着样本数量的增加而增加。而AMCM 在输出结果前增加了稳定性判断这一步骤，可以实时调整样本数量，采用更少的样本数据即可得到准确可靠的输出量，因此使用AMCM可以解决输出量的准确度和样本计算时间的矛盾。

2.2 测量不确定度评定结果

基于不确定度评定模型，得到基线边长度分别为72、216、432、624、1 176 m 时，全站仪观测值的不确定度评定结果如表2所示。

表2 不确定度评定结果Tab.2 Uncertainty evaluation results

表2中，ΔD0为基线边长度；E为不同测距长度下全站仪观测值的最佳估计值；U为不同测距长度下全站仪观测值的扩展不确定度，包含因子k= 2；［c1，c2］为95%置信概率的包含区间的左右端点。

该过程中试验次数h= 3，即样本数量M= 3 ×105时，结果已经趋于统计稳定，相比蒙特卡洛法的样本数量M至少需要106个减少了70%的样本数量，且二者的不确定度评定结果相同，基线边长度分别为72、216、432、624、1 176 m 时测量结果分布分别如图2 ～ 6所示。

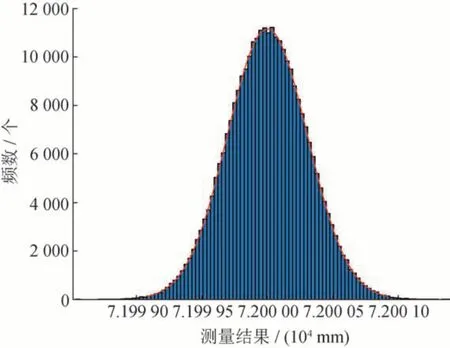
图2 72 m测量结果分布Fig.2 Distribution of 72 m measurement results

图3 216 m测量结果分布Fig.3 Distribution of 216 m measurement results

图5 624 m测量结果分布Fig.5 Distribution of 624 m measurement results

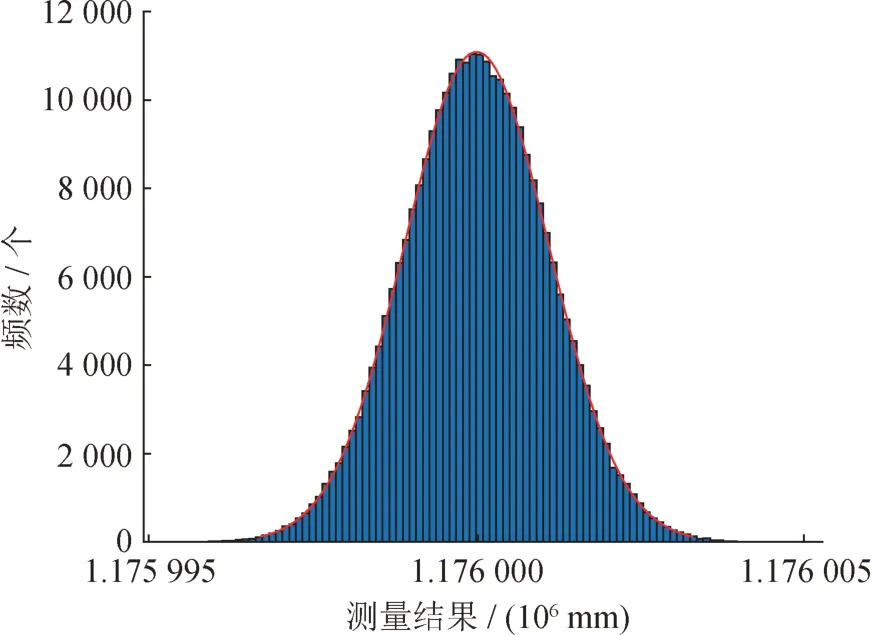
图6 1 176 m测量结果分布Fig.6 Distribution of 1 176 m measurement results

3 评定结果验证

3.1 GUM评定结果

全国测距仪校准能力计量比对试验在中国计量科学研究院昌平基地标准基线上进行，采用“固定地点”比对方式，比对的基线边长度分别为72、216、432、624、1 176 m。测量结果如表3 所示，使用GUM 评定全站仪测距的扩展测量不确定度为0.5 mm + 1.87 mm/km ×D（k= 2）。

表3 测量结果Tab.3 Measurement results

表3 中，D为全站仪经过频率、气象、倾斜和乘常数修正后的观测结果；dev为全站仪观测结果与参考值比较的等效结果，每段基线共测量10次，每次测量同步记录主导实验室提供的实时环境参数数据，经环境参数补偿后，取平均值作为每段基线边长度的观测结果；UGUM为通过GUM 评定的各基线边标准长度的扩展测量不确定度。

3.2 结果对比

由2.2 节AMCM 测量不确定度评定结果和3.1节GUM 评定结果可以看出：在测距距离较短时，二者的测量不确定度接近，如测距距离为72 m 时，二者的测量不确定度相同；在测距距离较长时，AMCM 的测量不确定度评定结果小于GUM，如测距距离为216 m时，AMCM的测量不确定度比GUM小0.2 mm，距离为1 176 m 时，AMCM 的测量不确定度比GUM 小0.4 mm，AMCM 和GUM 两种不确定度评定方法评定的扩展不确定度对比如图7 所示。其中偏差为0 的黑线为基线边长度的参考值，从图7中可以看出，两种不确定度评定方法的测量结果均在合理预期之内。

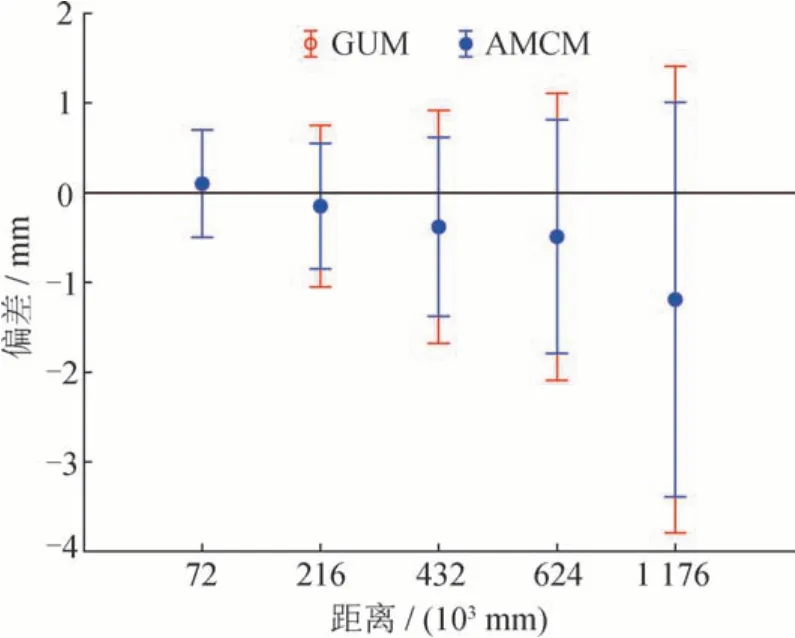
图7 GUM和AMCM评定不确定度结果对比Fig.7 Comparison of uncertainty evaluation results between GUM and AMCM

造成AMCM在测距距离较长时的扩展不确定度小于GUM 的原因是：GUM 假设各误差源之间互不相关，而仪器随机测量误差引入的测量不确定度分量中包含了基线参考值、环境参数和仪器参数引入的部分测量不确定度分量，且随着测距距离的增加，该部分引入的不确定度分量也随之增加，导致GUM评定的扩展不确定度可能被保守估计。