数据采集系统输入电阻的不确定度分析与评定

梁志国，冯秀娟

（1.航空工业北京长城计量测试技术研究所 计量与校准技术重点实验室，北京100095；2.中国计量科学研究院 力学与声学计量科学研究所，北京100029）

0 引言

电压类测量仪器的测量原理简言之是将其并联入被测对象的电路之中，测量并获取被测对象的电压。因而，输入阻抗是非常重要的性能指标。在输入阻抗中，电阻分量居主导地位，电抗分量往往非常微小，可以忽略，故多数情况下的输入阻抗测量是指输入电阻的量值测量，尤其是高阻状态。

通常，电压类测量仪器的设计应用遵循两种不同理念，一种为高阻设计理念，主要用于100 MHz 及以下的中低频率范围，以集总参数元器件为核心的电路理论为基础的仪器仪表；相比于被测量对象的内阻，测量仪表的输入电阻特别巨大，在测量过程中，给被测对象带来的影响很微小，可以忽略不计，例如数字电压表［1］、100 MHz 及以下带宽的示波器。另外一种为匹配设计理念，输入电阻（输入阻抗）通常为50 Ω；主要用于中高频率及以上的频率范围，以分布参数效应元器件为核心的电磁场理论为基础的仪器仪表，如瞬态波形记录仪，宽带示波器等等［2］。相比于所测对象，其阻抗具有相同的量值，因而在较低频率情况下，能从被测对象处获取最大的信号功率，而在较高频率情况下，对被测对象造成的电能量反射最少。

直流以及中低频率测量仪器多采用高阻设计，而射频及微波频率范围测量仪器全部采用匹配设计方案。数据采集系统多数属于中低频率测量范畴，通常使用高阻输入的设计方案。但仍然有少数称为高速数据采集系统的仪器，其模拟带宽可达100 MHz以上，使用了匹配设计模式，并且具有直流耦合和交流耦合两种不同的耦合方式。

输入阻抗测量可使用RLC 测量仪、交流电桥等仪器直接测量，并以某种简单的等效电路形式给出其参数，如电阻与电容并联形式分别给出电阻和电容值，电阻与电感串联形式分别给出电阻和电感值；也可使用阻抗分析仪、矢量网络分析仪、时域反射计等仪器分析获得［3-4］。

通常，匹配传输设计的输入电路使用阻抗参数表征［5-7］。高阻传输设计的输入电路主要使用输入电阻参数表征［8-13］。由于阻抗会随频率不同而变化，但输入电阻则具有相对的稳定性与一致性，故在高阻抗电路中常被作为测量对象［14-19］。同时，针对输入电阻测量的改进研究也曾经不断涌现［20-22］，其中包括输入电阻带来的误差影响［23-27］。

本文主要讨论数据采集系统输入电阻计量校准中的问题及其不确定度评定。

1 测量原理与方法

数据采集系统输入电阻测量原理为欧姆定律［28］。如图1 所示接线，选择标准电阻R为与数据采集系统输入电阻标称量值Ri相当的值（一般为（0.1 ～ 10）Ri），将被校采集通道通过标准电阻R接到直流电压信号源上。

图1 校准输入电阻的接线图Fig 1 Input resistance calibration diagram

设置直流电压源信号幅度E=E1，加载信号，启动采集，记录采集数据x1j，（j= 0，…，n-1），折合到输入端的测量幅度值U1为

式中：n为每个通道采集数据个数；G0为测量通道的增益值。

将信号幅度调置为E=E2，加载信号，启动采集，记录采集数据x2j，（j= 0，…，n-1），折合到输入端的测量幅度值U2为

按式（3）计算数据采集系统通道输入电阻Rin。

其中，E1、E2的选取原则是使得对应的测量值U1、U2两者之差越大越好，从而降低输入电阻的测量不确定度。

2 测量不确定度模型

由式（3）可见，输入电阻Rin与信号幅度E1、E2、U1、U2以及标准电阻R均有关，因此，可以列出输入电阻Rin测量不确定度的主要来源为：①信号幅度E1、E2之差ΔE0的不确定度u（ΔE0），主要由标准信号源的误差造成；②信号幅度U1、U2之差ΔU0的不确定度u（ΔU0），主要由标准信号源的误差和测量系统自身造成；③标准电阻R的测量不确定度u（R），主要由标准电阻R的误差等因素造成。

由式（3）可得

灵敏系数为

测量过程中，假设输入电阻Rin测量不确定度的不同分量之间不相关，根据输出测量值对于输入量的测量值的不确定度传递公式［29］，由式（8）获得其合成标准不确定度uc（Rin）为

由式（9）获得其相对合成标准不确定度urel（Rin）为

由式（15）可见，输入电阻测量不确定度为标准直流电压ΔE0不确定度、测量电压ΔU0不确定度和标准电阻R不确定度的合成，其传递系数c0则由输入电阻与标准电阻的比值Rin/R确定，为降低其测量不确定度，除了标准直流电压源的不确定度和标准电阻的不确定度要求外，需要选取输入电阻与标准电阻的比值（Rin/R）足够小，通常要求R≥Rin。

3 测量数据及处理

选取NI USB-4431型数据采集系统作为被测对象［30］，共有4个差分输入通道，量程范围为±10 V，24 位A/D，最大允许误差为±0.15%，采集速率1 ～102.4 kSa/s，标称输入电阻200 kΩ。选取通道1作为测量通道，其通道增益标定为G0= 1.002 857。

以9500B 型示波器校准仪作为直流电压标准源［31］，幅度范围为±（10 mV ～ 10 V），最大允许误差为±0.03% ～ ±0.001%。选标准电阻R= 200 kΩ，最大允许误差±0.01%，误差在［-0.01%，+0.01%］范围内服从均匀分布，相对不确定度为

给数据采集系统通道1 分别加载E1= 7.000 V，E2= 9.000 V，设置采集数据个数n= 100。获得采集测量结果，用式（1）、（2）计算得U1、U2，用式（3）计算得输入电阻Rin，如表1所示。

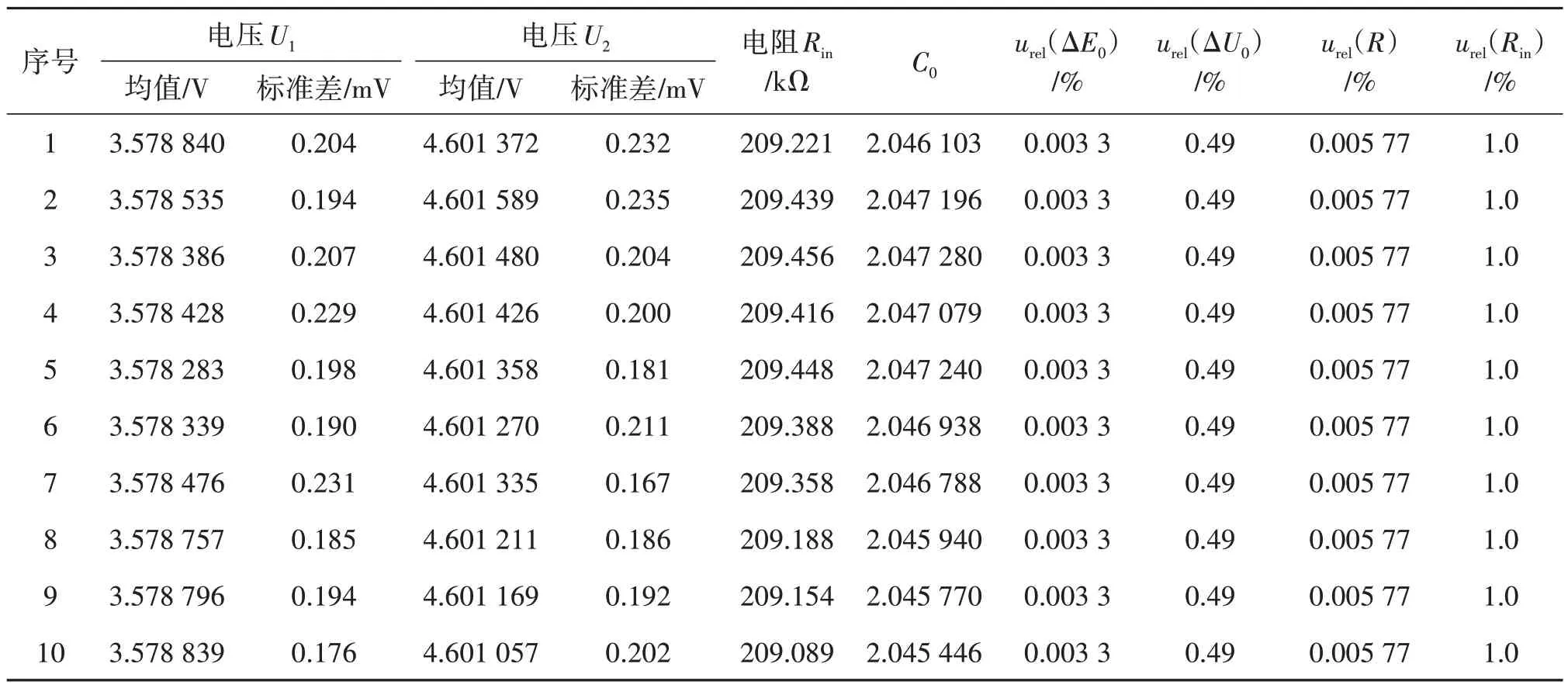
表1 输入电阻测量结果Tab.1 Input resistance measurement results

按照直流标准源9 500B 的指标，设E1和E2的最大相对误差均为±0.001%，并假设均服从均匀分布。则，

E1的最大允许误差为

E1的不确定度为

E2的最大允许误差为

E2的不确定度为

ΔE0=E2-E1的不确定度为

按照数据采集系统NI USB-4431的指标，设U1和U2的最大相对误差均为±0.15%，并假设均服从均匀分布。则

U1的最大允许误差为

U1的不确定度为

U2的最大允许误差为

U2的不确定度为

ΔU0=U2-U1的不确定度为

计算结果如表1所示。

4 合成不确定度

通过式（13）计算灵敏系数，按照式（15）计算合成标准不确定度相对值urel（Rin），如表1所示。

从输入电阻Rin的10 次测量结果可见，实验标准偏差为0.14 kΩ，与输入电阻之比为0.067%，与urel（ΔU0）相比，可以被忽略。因此，Rin测量重复性造成的不确定度可以忽略，从单次测量获得的结果及不确定度可以完整表征Rin的测量。

5 扩展不确定度及测量结果

将表1 中各个不确定度分量集中列出，如表2所示。

表2 不确定度分量概算表Tab.2 Estimation table of uncertainty components

从表2 中各个不确定度分量的量值水平来看，存在主导分量urel（ΔU0），其量值水平占据主导地位且量值服从梯形分布，由此可认定，合成标准不确定度相对值urel（Rin）近似服从梯形分布。

由于U1的误差在区间［-ΔU1，ΔU1］ = ［-5.37 mV，+5.37 mV］内服从均匀分布，U2的误差在区间［-ΔU2，ΔU2］= ［-6.90 mV，+6.90 mV］内服从均匀分布，则其差值ΔU0=U2-U1应服从梯形分布，其上下底之比为

取置信概率p= 95%，则有包含因子［32］

k95= 1.89，则扩展不确定度为

数据采集系统的输入电阻为

其中，“±”后面是输入电阻的扩展不确定度，包含因子k95= 1.89，是由梯形分布假设以及置信概率p= 95%的要求计算获得。

6 结论

输入电阻的测量不确定度主要来自标准电压源、输入端测量电压和标准电阻的合成结果。实际工作中输入电阻的不确定度往往非常大，不知缘故。

输入电阻的相对不确定度为ΔE0的不确定度u（ΔE0）和ΔU0的不确定度u（ΔU0）以及标准电阻R的测量不确定度u（R）的加权合成，权值c0则由输入电阻与标准电阻的比值Rin/R确定。此比值不宜过大或过小，过小时，电位差的不确定度变大，过大时，权值变大，产生不确定度的放大效果。因此，Rin/R量值在1附近为较佳选择。

在本组实验的条件下，数据采集系统的测量误差占主导地位。若想降低输入电阻的测量不确定度，除了平衡标准电阻、输入幅度E1和E2和测量幅度U1和U2等各个物理量不确定度的贡献，从而寻求最佳状态以外，还可以使用高精度数字电压表来替代数据采集系统测量获得U1和U2，以降低输入电阻的测量不确定度，即通过选取电压源、标准电阻以及测量电压的方式控制测量结果的不确定度。

在实际工作中，使用数字电压表进行测量还应考虑其输入电阻对被测电路带来的额外负载效应的影响。