单杆液压缸电液位置伺服系统物理建模与分析*

张贻哲,李跃松,李阁强,李贵飞,王 棒

(河南科技大学机电工程学院,河南 洛阳 471003)

由于单杆液压缸具有占用空间小,结构简单,承载能力大以及制造成本比较低廉等一系列优点[1],所以,对称阀控制非对称缸电液伺服位置系统在工程中应用非常广泛,如用于船舶、飞机、大型的机械设备以及多自由度的模拟器等[2]。阀控单杆液压缸系统模型仿真经过多年的研究累积,产生了很多的数学模型[3]。但其数学模型复杂,很难精确分析系统的一些因素,所以对阀控制单杆液压缸伺服系统建立物理模型,可以进一步对系统进行有效的仿真分析。在建立的数学模型基础上,结合实际情况,添加准确的泵、位移传感器等模块,并进行参数设置,使系统模型的仿真更为全面,更符合实际情况,可以有效地观测出在实际工作环境的条件下,系统物理模型仿真出来的结果是否符合工程上要求的控制性能[4-5]。对称阀控制单杆液压缸位置伺服系统建立的物理模型需要的条件精度更高,与数学模型比较后发现:数学模型偏向于理论,缺少对其他的一些干扰以及摩擦之类情况的准确判断,而物理模型采用与系统工程设计过程较为相似的建模方式[6],更符合真实物理系统的结构组成以及控制特性,模型更为准确,更有利于分析实际的电液位置伺服系统的控制性能。

对单杆液压缸电液伺服系统进行物理建模仿真的方法之一就是利用Simulink仿真软件进行仿真。Simulink仿真可以轻松地建立模型,操作简单,效率高,同时仿真结果很明显[7-8]。对阀控单杆液压缸电液位置伺服系统利用Simulink仿真软件建立物理模型,分别在正弦信号和方波信号的输入曲线下,设置好各个模块的参数,输出阶跃响应曲线图和Bode图,分析其动态特性,通过系统的仿真结果来分析观察出系统物理模型的响应性能。

1 单杆液压缸电液位置伺服系统

阀控单杆液压缸电液位置伺服系统如图1所示,由非对称液压缸、电液伺服阀、控制器、位移传感器、伺服放大器以及负载组成[9]。

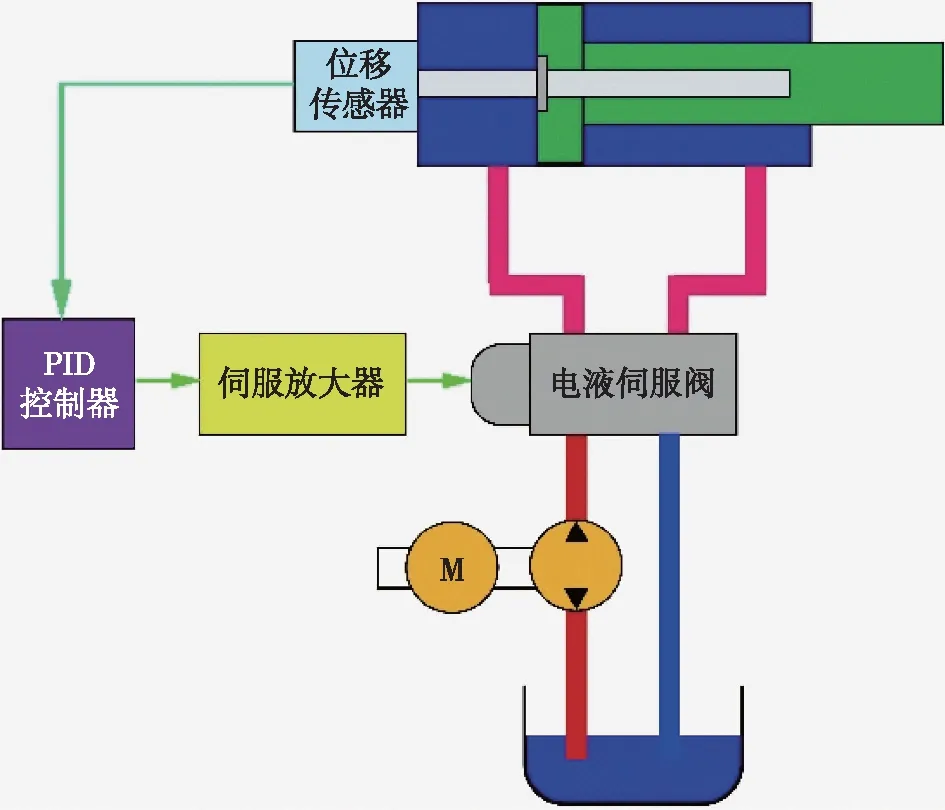
图1 电液位置伺服系统控制原理图Fig.1 Electro-hydraulic position servo system control schematic

电液位置伺服系统中,控制器将接收到的指令信号与传感器测量的反馈信号比较,将误差信号传递给电液伺服阀,电液伺服阀接收到信号后,阀芯开始移动,控制阀口的开度,液压油通过电液伺服阀阀口,从而控制进入单杆液压缸油的流量和压力,液压油推动油缸的活塞移动,形成闭环控制运动[10-11]。本文所要仿真的电液位置伺服系统控制原理如图1所示,系统的控制原理框图如图2所示。

图2 系统的控制原理框图Fig.2 Block diagram of the control principle of the system

2 单杆液压缸电液位置伺服系统物理模型

依据图1可以建立单杆液压缸电液位置伺服系统的物理模型,该物理模型是由油源、动力元件、传感器以及负载组成。油源则是由定量泵、油箱、溢流阀、管道等组成;动力元件则包括电液伺服阀和单杆液压缸,阀和缸用管道连接起来;传感器则包括位移传感器、力传感器、机械线性弹簧、粘性阻尼器等。物理模型如图3所示。

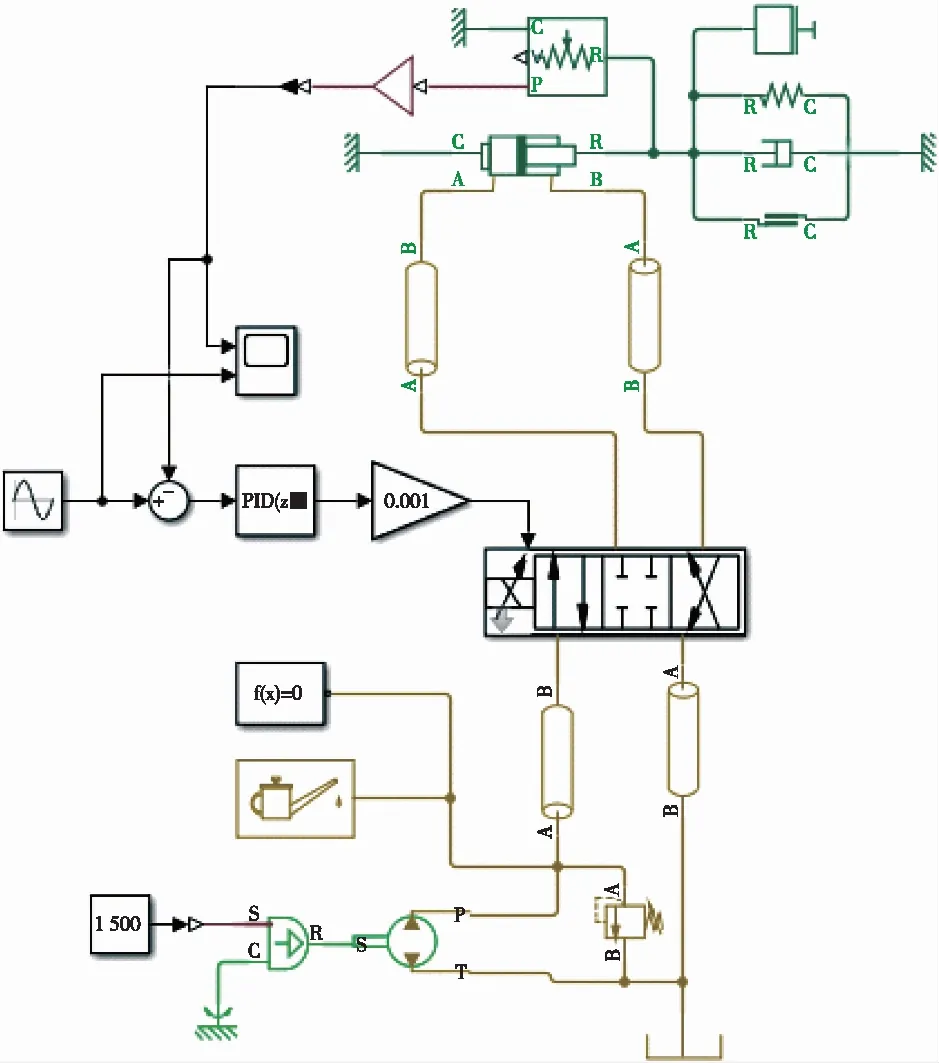
图3 系统的物理模型Fig.3 Physical model of the system

在此系统建立的物理模型中,电液伺服阀是由电机械转换装置和节流孔封装成的一个模块,可以直接使用,物理模型如图4所示。

图4 电液伺服阀物理模型Fig.4 Physical model of electro-hydraulic servo valve

根据需要设置电液伺服阀的固有频率、阻尼比以及阀的额定流量、额定电流、额定压力,如图5所示。

图5 电液伺服阀物理模型参数设置Fig.5 Electro-hydraulic servo valve physical model parameter settings

Simulink电液伺服系统元件的物理模型如表1所示。

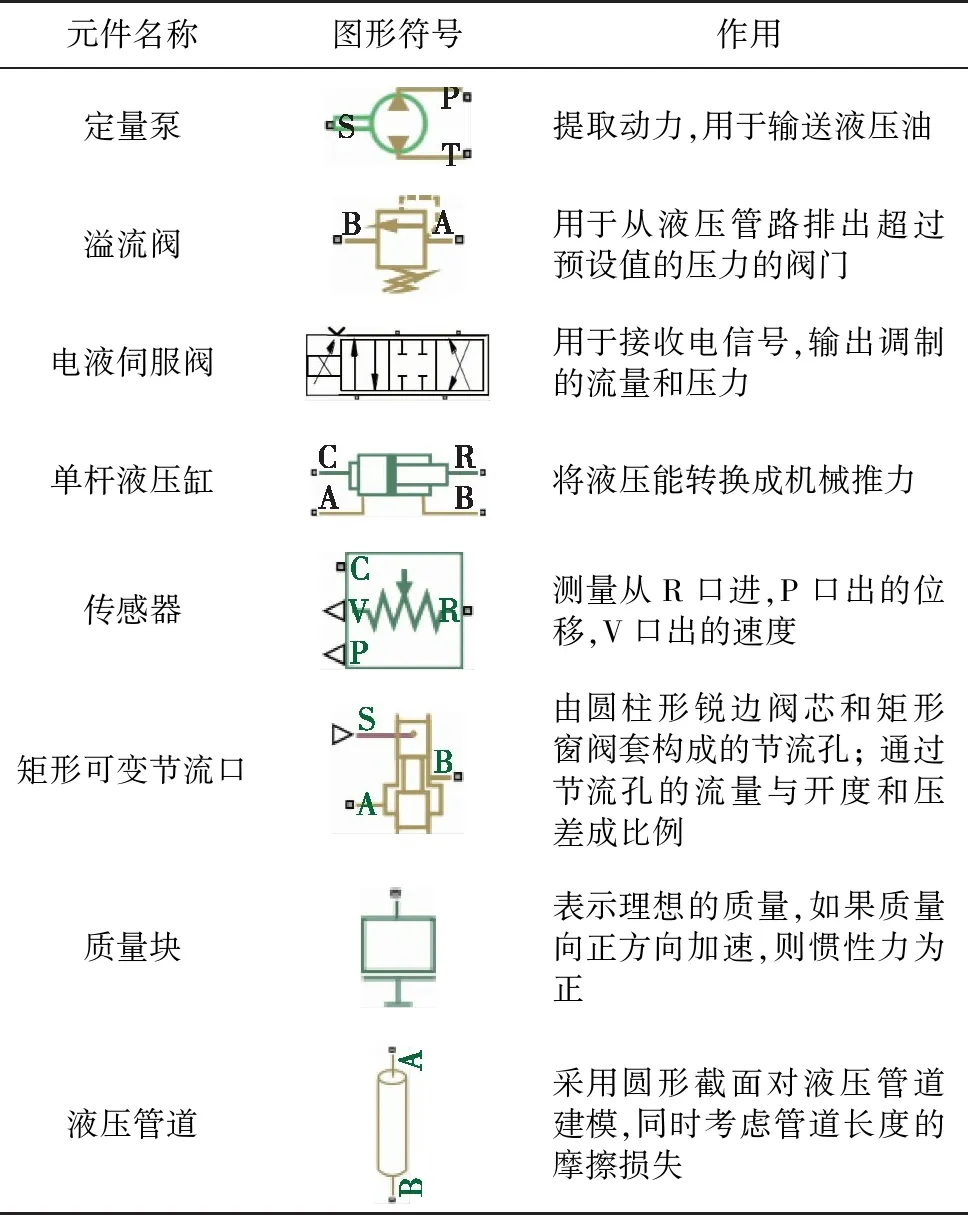
表1 Simulink电液位置伺服系统物理模型元件Tab.1 Simulink electro-hydraulic position servo system physical model components

3 物理模型仿真分析

3.1 系统参数设置

Simulink建立阀控单杆液压缸电液伺服系统物理模型后,分别在开环控制和闭环控制下,输入正弦信号和方波信号,得到响应曲线图,系统的各参数如表2所示。

3.2 仿真结果分析

首先,在系统开环控制下,对电液伺服阀输入频率为0.8 Hz,振幅为±10 V的正弦信号和峰值为±10 V的方波信号,得到系统的响应曲线图,包括单杆液压缸活塞位移特性曲线和速度特性曲线。

正弦信号输入后的系统响应特性曲线如图6所示。方波信号输入后的系统响应曲线如图7所示。

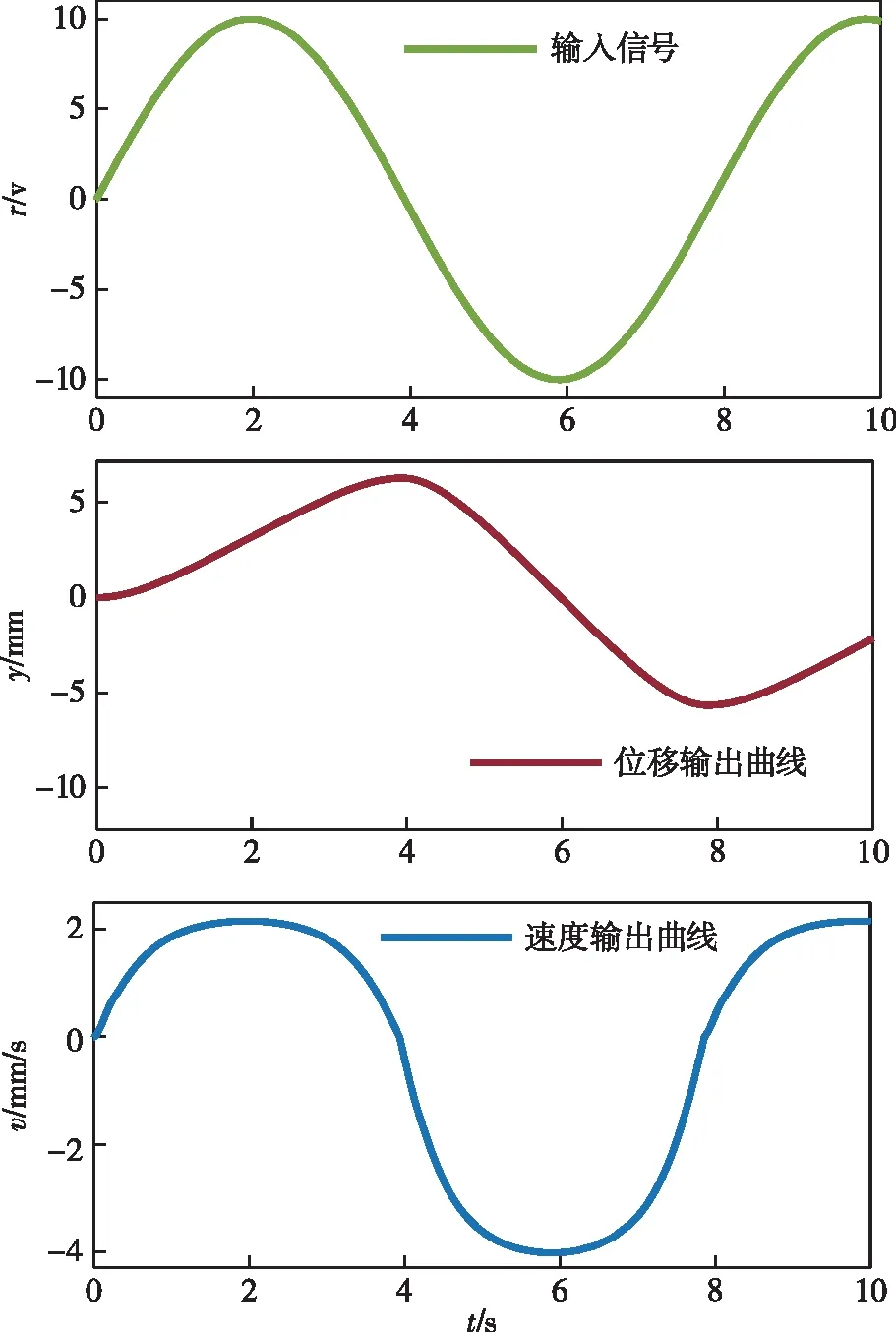
图6 开环控制下正弦响应特性曲线图Fig.6 Sine response characteristic curve under open loop control

图7 开环控制下方波响应特性曲线图Fig.7 Plot of square wave response characteristics under open loop control

从图6和图7中的位移特性曲线图可知,系统在开环控制下,输入指令信号为正弦信号和方波信号后,若指令为正信号,液压缸活塞位移逐渐增大,若指令为负信号,液压缸活塞位移逐渐减小,响应慢,且都不能达到指令信号的位置,精度低,控制效果差。从图6和图7中的速度特性曲线图可知,在开环控制下,单杆液压缸活塞伸出和缩回的移动速度不一致,向无杆腔方向移动速度快,向有杆腔方向移动速度慢,导致活塞杆位移未能准确到达指定位置,系统控制精度低。

开环控制下,电液位置伺服系统的性能较差,需要进行闭环控制。闭环控制一般采用PID控制进行校正,通过调整比例、积分、微分系数,使系统可以达到较好性能。

闭环控制校正后,同样对物理模型输入振幅为±10 V的正弦信号和峰值为±10 V的方波信号,得到位移输出特性曲线图。闭环控制的情况下,正弦信号响应曲线图如图8所示,方波信号响应曲线图如图9所示。

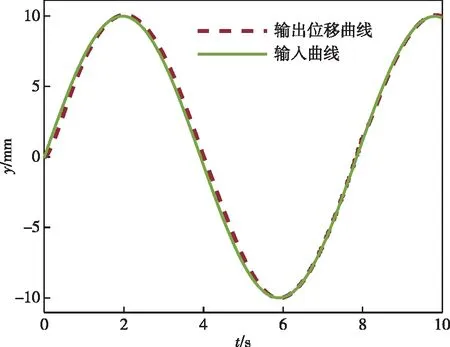
图8 闭环控制下正弦响应曲线图Fig.8 Sine response graph under closed loop control

图9 闭环控制下方波响应曲线图Fig.9 Plot of square wave response under closed loop control

由图8和图9可知,校正后闭环控制下,系统的性能明显提高了很多,响应曲线跟踪性能好,准确性得到了提高,误差减少,可以达到很好的控制效果。从图9方波响应曲线图可得,在额定输入阶跃信号下,系统存在较小的超调量,峰值时间为0.798 s,进入稳态的时间为1.125 s。建立系统的物理模型可以解决数学模型复杂,不利于分析一些因素等问题,仿真出来的结果更符合实际,有利于对系统的控制性能进一步深入研究,从而提高工作效率。

在物理模型仿真中,同样可以对系统进行Bode图分析。Bode图是一种可以帮助确定系统是否稳定的图,并可以分析系统特性。Bode图分为高、中、低三个频段,低频段的斜率越小,位置越高,系统的稳态精度越高;中频段若有较大的带宽,系统的动态性能较好;高频段衰减得越快,系统抗干扰能力越强[12]。

系统校正闭环控制后,闭环Bode图如图10所示。

图10 系统闭环控制的Bode图Fig.10 Bode diagram for closed loop control of the system

由图10可知,对系统进行PID矫正控制,形成闭环控制后,幅值裕量Kg=11.6 dB,相位裕量θ=180°-135°=45°。相位裕量大于零,系统稳定,且大于40°,满足一般工程上的要求,稳定程度较高。在对液压伺服控制系统矫正时,可以采用PID矫正、速度和加速度反馈矫正等以达到提高系统性能的目的。从建立的单杆液压缸电液位置伺服系统物理模型仿真结果中可以分析出系统的位移特性和速度特性,显而易见,闭环校正后系统的响应时间得到提高,系统比较稳定。物理模型所需要考虑的因素与实际情况相同,仿真结果也更符合实际工作环境中的控制效果,对于实际系统操作分析更具有参考价值。

4 结束语

为了解决由于单杆液压缸电液位置伺服系统的结构不对称,建立的数学模型较为复杂,无法利用数学方法来精确分析很多因素的问题,本文利用Simulink仿真软件建立了系统的物理模型。仿真过程可以得出结论:

1)建立系统的物理模型可以直接加入影响系统性能的元件包括电液伺服阀、液压缸、管道、传感器和泵等一些模块,同时对模块进行参数设置,仿真条件的准确度更高,仿真结果更符合实际系统控制效果,更为精准。同时,可以根据不同信号的输入,得到响应曲线图以及Bode图,能够有效地分析系统的性能,提高效率,不需要复杂的传递函数和计算,对系统研究分析是一种更有效且准确性更高的方法。

2)从物理模型仿真结果可以看出,单杆液压缸电液位置伺服系统在开环控制下,活塞杆伸出和缩回的速度不一致,位移量不能达到指定信号,控制精度低,进行PID控制矫正,形成闭环控制后,可以有效提高系统的控制性能。