一种适用于海上通信的OFDM系统信道估计算法

刘 阳, 杨 蕾*, 吴志强

(1.武汉轻工大学 电气与电子工程学院, 湖北 武汉 430023; 2.北京大学 武汉人工智能研究院, 湖北 武汉 430073)

0 引言

相比于陆地无线通信,海上无线通信中存在着信号衰减和信号失真等问题,且海上通信中噪声极大的问题较为突出,海洋中存在各种自然噪声源,如风浪、船舶和海洋生物的声音,这些噪声会使得信号质量受到影响,例如信号强度变得不稳定、信号畸变等.这将导致信号传输的可靠性下降,从而降低通信质量.目前海上贸易日趋频繁,伴随着船舶上各类智能化设备不断增多,通信数据也迅速增长,海上通信的需求显得更为迫切[1-3].正交频分复用作为一种平行多载波调制技术,由于其具有频谱利用率高,抗干扰能力强的优点,在海上通信领域得到了广泛的应用.

对于OFDM系统而言,当信号被发送时,由于海上无线信道具有不可控性、随机性等特点,这将大大地影响海上通信质量,一般需要对发送时的信道状态进行估计,以提高接收信号质量[4,5],现已有几种较为经典的信道估计算法被提出.

LS算法[6]在实际系统中使用较多,该算法具有计算方便,复杂度低,无需了解任何先验信道信息等特点,但LS算法受噪声影响大,在低信噪比时性能较差.最小均方误差(Minimum Mean Square Error,MMSE)算法表现最佳[4],该算法可获得准确的信道估计,但MMSE算法需已知信道统计信息,这些信息在突发通信系统中较难获取.线性最小均方误差(Liner Minimum Mean Square Error,LMMSE)算法[7]是MMSE的改进算法,其仍存在运算复杂度大的问题.基于离散傅里叶变换(Discrete Fourier Transform,DFT)的信道估计算法[8]是LS算法的改进算法,该算法大大改善了LS算法性能.DFT算法先将LS算法所得频域信道响应进行傅里叶反变换,再依据在循环前缀(Cyclic Prefix,CP)内能找到大部分的信道信息,从而对循环前缀外的值进行置零来消除时域噪声,再进行DFT变换来重新获得频域信道估计结果.DFT信道估计算法具有计算方便、无需已知信道先验信息等特点,其性能比LS算法更优.但传统DFT算法在信道估计中对噪声的处理仅去除了循环前缀外的噪声,且是以LS算法为基础,其性能受噪声的影响较大,需进一步改进.文献[9]是近些年提出的一种利用训练序列对DFT算法进行改进的信道信噪比估计算法,其对于突发通信系统中大脉冲噪声的影响能够进行有效应对,该算法在处理时需要进行大量的计算,因此其计算量较大[9],虽性能较传统算法有所提升,但对于噪声方面的考虑依旧有所欠缺.

针对DFT信道估计算法对抑制噪声方面的缺陷,本文提出一种基于多域降噪的信道估计算法.此算法在频域上对LS算法所得结果进行小波包降噪,然后在DFT信道估计循环前缀内建立阈值门限,循环前缀外数据置零,循环前缀内数据经过门限处理来压制噪声干扰,最后在变换域再进一步消噪,联合多种降噪方法,来提高DFT信道估计算法性能.

1 海上OFDM系统原理

1.1 海上多径信道

由于海水介质的损耗、反射、散射和折射等多种因素,海上信道通常呈现多径传播的特征,即信号会经过多条路径传输到达接收端.不同路径间的信号相互干扰,导致信号的接收质量下降.

海上信道模型通常可看作是具有多种路径的信道,海上多径衰落信道接收关系式可表示为:

(1)

式(1)中:y(t)表示接收信号,x(t)表示发送信号,τi表示第i条路径的传播时延,hi(t)表示第i条路径的时变复数增益,w(t)表示加性高斯白噪声.

海洋环境的复杂性和多变性也会导致海上信道通信的传输特性在时间和空间上存在很大的变化,这对通信系统设计和信号处理来说都是一大挑战.

1.2 OFDM系统原理

就海上无线通信传输系统而言,选用抗多径衰落干扰的通信系统十分有必要,与其它海上通信方式相比,采用OFDM传输系统可以使海上通信更快捷,更高效[10].

OFDM系统的基本思路是把信道划分为多个正交的子信道[11-13],将需要传输的高速数据信号进行并行转换为较低速的数据流,并将这些数据流分别调制到不同的正交子载波上,彼此正交的子载波能较好地规避子载波间干扰,频谱之间也可以相互重合,从而使带宽被充分利用,并通过插入循环前缀来避免符号间干扰问题.在接收端,通过一定方式对各个子载波进行解调和分离,得到原始数据流.并且由于各子信道中带宽只占原有信道带宽很小一部分,所以后面的信道均衡也就比较容易实现.

图1所示为OFDM系统原理图.信号在频域中收发过程关系式为:

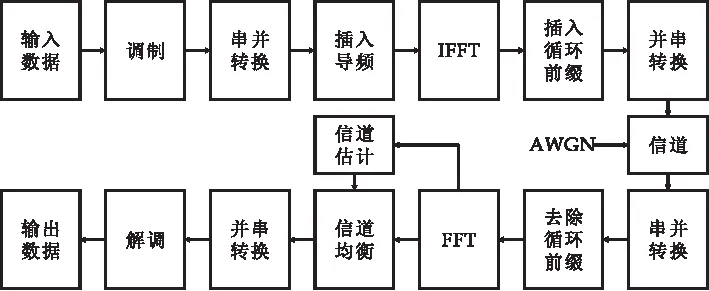
图1 OFDM系统原理图

Y=XH+W

(2)

式(2)中:Y代表接收端收到的信号,X代表发射端的已知信号,H代表信道的频率响应,W代表通信过程中的噪声.

OFDM系统发送端输入数据经QPSK调制,以复数形式进行串并转换获得N路并行数据,插入导频获得复数信号X(k),再让信号经快速傅里叶变换(Fast Fourier Transform,IFFT)对多路正交子载波实现OFDM系统调制[14],表达式为:

(3)

接收端在去掉循环前缀后,用FFT进行解调,第n个子载波上的数据可表示为:

(4)

2 OFDM系统的信道估计

2.1 选取导频插入图样

三种插入导频的方案如图2所示,分别为块状导频、梳状导频以及格状导频,其中黑色表示导频符号,白色表示数据.

图2 各类导频图样

块状导频因其频域分布的连续性,适合在频率选择性衰落信道中使用,此种衰落在海上通信中最易出现,而文章正是采用了这种导频方式[15].

2.2 基于LS的信道估计算法与噪声缺陷

LS算法作为一种复杂度较低的算法,是通过最小二乘法获得的[6],可由接收发送的信号直接得到信道响应.LS算法是要找到使收发关系式的代价函数最小的信道响应.代价函数可表示为:

(5)

(6)

(7)

至此,LS信道估计的均方误差MSE可表示为:

(8)

式(8)可表明,LS算法的MSE跟信噪比成反比,说明其性能并不稳定,在大噪声条件下精度会受到影响.但因其结构简单,复杂度低,多种算法都是以此算法为基础衍生而出.

2.3 传统DFT信道估计算法

传统DFT算法对所得频域信道响应进行离散傅里叶反变换,获得时域信道响应后,将循环前缀外的响应置为0以消除噪声[16].算法框图如图3所示.

图3 传统DFT信道估计算法框图

对LS频域信道响应做IDFT:

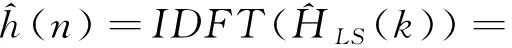
(9)

有用数据一般集中在信道冲击响应内,其长度小于循环前缀L,由于无法获得实际信道冲击响应长度,所以把循环前缀外数据置为0来尽可能地抑制噪声,其它数据则保留下来,表达式如下:

(10)

再进行DFT变换得到处理后的频域信道估计响应:

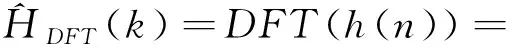
(11)

此信道估计算法较LS算法性能有所提升,但不能很好地抑制噪声,其估计性能需进一步改善.

2.4 多域降噪的信道估计算法

针对海上噪声问题,提出改进型算法--基于多域降噪的DFT信道估计算法,图4为总体改进算法框图.

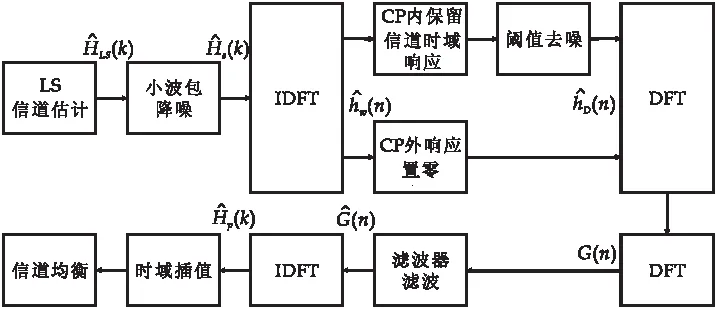
图4 改进DFT信道估计算法框图

2.4.1 频域降噪--小波包降噪

S=AAA3+DAA3+ADA3+DDA3+
AAD3+DAD3+ADD3+DDD3

(12)

图5为三层小波包分解示意图,A代表低频部分,D代表高频部分.

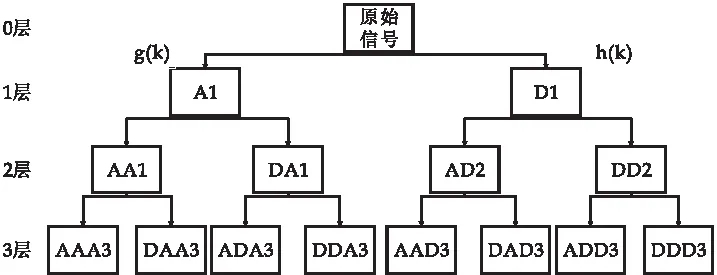
图5 三层小波包分解

小波包降噪作用于信号的程序如下:

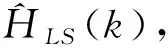
(13)

式(13)中:si,2j-1(k)为细节系数,si,2j(k)为近似系数,下标i,j代表第i层的第j个节点对应于要分解的信号,g(k)表示低通滤波系数,h(k)表示高通滤波系数,二者需满足式:

g(k)=(-1)kh(1-k)

(14)

(2)定义最优小波包基,通过熵标准来计算最优树,可获得最适合问题的小波包基.

以有用信号定义代价函数为:

(15)

使用对数能量熵作为代价函数可以更好地衡量小波包系数和原始信号之间的逼近误差和重构误差,进而选择最优小波包基,从而更好地实现信号去噪处理.

(3)选择适合的阈值对小波包分解因子进行阈值量化操作.

软阈值处理函数:

(16)

式(16)中:λ为阈值,sgn(·)函数是一个数学函数,表示为函数内的值大于0时返回1,等于0时返回0,小于0时返回-1.

(4)对小波包进行重构操作.

(17)

2.4.2 时域降噪--阈值降噪

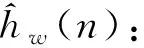
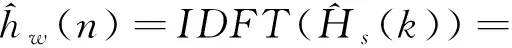
(18)

随后对时域范围信号做去噪处理.要分辨有效值和噪声值就必须设定一个合理门限.为了能最大限度地消除循环前缀噪声,同时保留尽可能大的有效信号,提出一种改进阈值处理方法:先取循环前缀以内的全部信道响应振幅模中位值为阈值部分,再考虑取循环前缀以外的全部信道响应振幅模平均值为阈值部分,最终得到两者之和再乘以合适的系数α作为最终阈值[19].需要注意的是α并没有一个固定的取值,它的具体取值需要根据实验和经验进行调整.为了得到较为稳定的信道估计结果,在实际应用中不断调整α的值,并根据实验结果进行相应的优化和调整.本文取α为0.5得到的实验结果较为出色.定义D1、D2、D为:

(19)

(20)

D=α·(D1+D2)

(21)

(22)

2.4.3 变换域降噪--滤波器降噪

(23)

图6是G(n)的索引图.由能量分布图可以看出,信号能量多分布于n=0、n=N-1左右,而噪声则存在于整个变换域内.设置一个低通滤波器使得变换域中的高频对应部分的G(n)置为0,可得到:

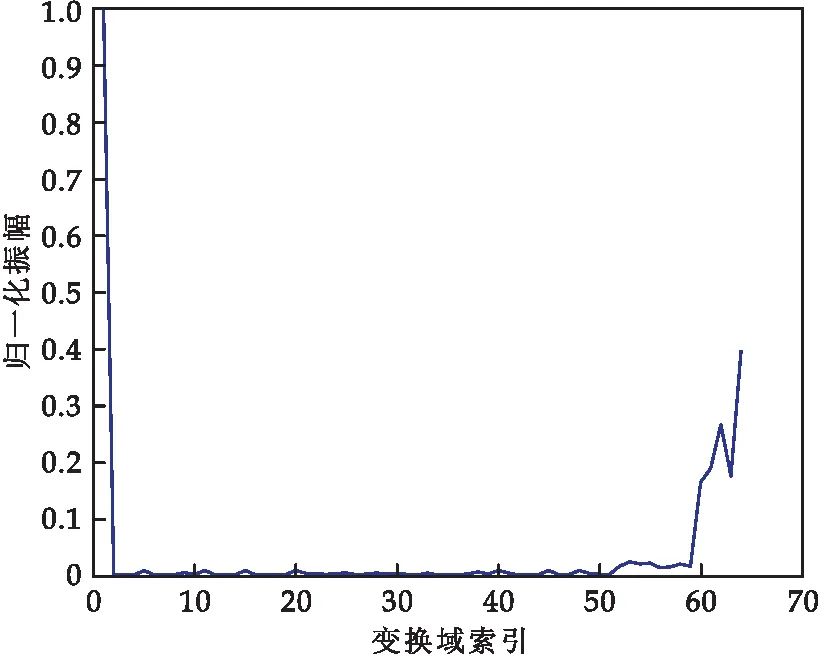
图6 G(n)的能量分布图

(24)

式(24)中:nc为1/2循环前缀长度.

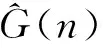
(25)

3 系统仿真分析

对文中提出的基于多域降噪的改进DFT算法进行了海上OFDM系统仿真研究.信道采用AWGN信道和海上多径衰落信道,详细参数如表1所示.系统参数的设定为:系统带宽为10 MHz,中心频率为30 MHz,基频为f0=75 Hz,采样频率为fs=153.6 kHz,码元长度为16.66 ms,信噪比SNR 的取值为-5 dB～20 dB.分别对无信道估计,LS算法,传统DFT算法,LMMSE算法,参考文献[9]DFT算法,本文改进DFT算法在信道频率响应幅值、星座图和误码率(Bit Error Rate,BER)方面进行仿真对比.

表1 系统仿真参数

分析图7中三种算法的信道频域响应幅度值可得:传统DFT算法对噪声的处理不够全面,导致信号出现了很多尖峰,变化幅度较大,波动较为明显,形态不平稳,信道频域响应受到噪声信号的干扰最为严重[14],参考文献中的DFT算法在做部分噪声处理后信道频域响应幅度值尖峰有所降低,能够更好地平滑信道频域响应,减小波动幅度,对噪声信号干扰有一定抑制作用,但是抑制效果不明显,尖峰仍大量存在.改进型信道估计算法在信道频域响应幅度上较传统算法有很大改善,表现最佳,响应幅度更加平稳、顺滑,尖峰大量减少,将噪声造成的影响降到了最低,跟踪信道性能也最稳定.

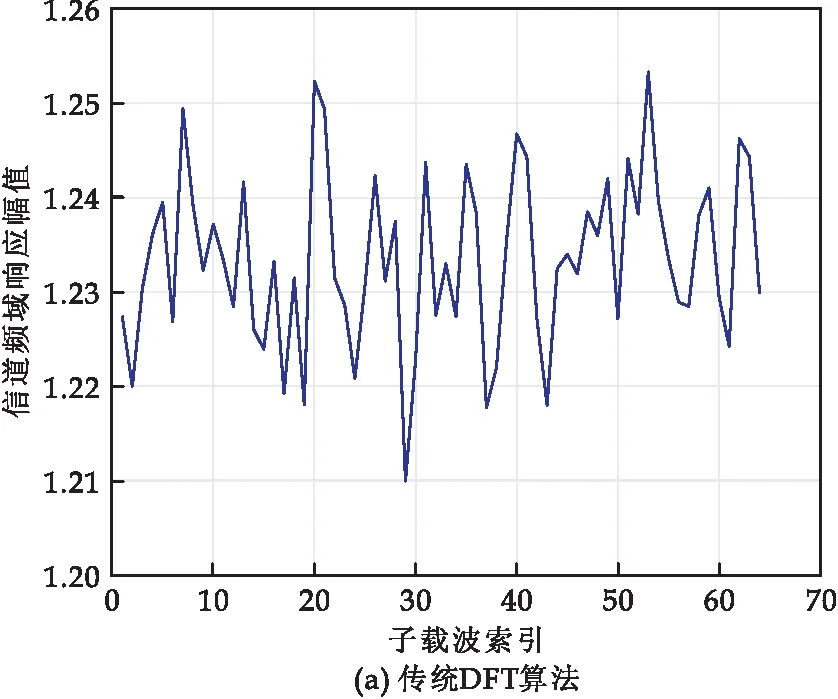
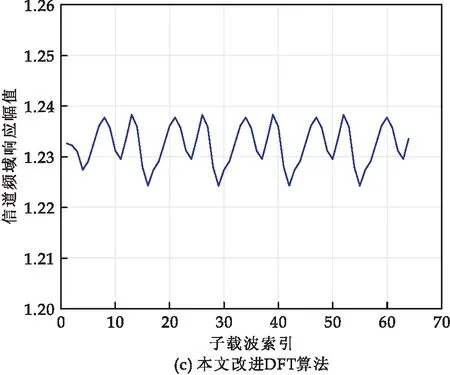
图7 不同算法的信道频域响应幅值比较

分析图8中不同算法信道补偿后的星座图可以发现:对于LS算法,由于其对噪声敏感,其算法信道补偿后得到的星座图畸变程度最大,星座点的分布较为离散,而且星座点之间的距离较大,这极有可能导致调制误码率较高.传统DFT算法比之LS算法在星座图上的表现稍有进步,星座点分布较为集中,且星座点之间的距离也比较小,这意味着其在提高调制精度方面有一定的优势,只是总体还是有待提升.本文的改进型算法得到的星座图表现最好,星座点分布最为稳定,同时星座点之间的距离差异也更小,这使得其在降低误码率方面具有非常好的性能,且在误差范围内准确地落在正确的位置上,与原本传输数据进行QPSK调制后的星座图最为相近.

图8 不同算法信道补偿后星座图比较

对图9中不同信道中各算法间误码率曲线关系进行分析:在AWGN信道下,信噪比在-5 dB到0 dB的范围内,传统算法的误码率在0.4左右,参考文献中的算法误码率可达0.3左右,改进算法误码率可达0.25,当信噪比提高时,不同算法之间的性能差距逐渐增大,信噪比在19 dB时,改进算法误码率可以达到2.9×10-6,在多径衰落信道下,信噪比在19 dB时,改进算法误码率可以达到2.8×10-2,在误码率为10-1时,本文改进DFT算法较之参考文献算法有近1.5 dB的提升,较之传统算法有近2 dBd的提升.在信噪比较高处显示性能仅次于LMMSE算法,其性能无论是在多径衰落信道下还是在AWGN信道下表现得都比传统算法好很多,且没有LMMSE算法的复杂性,所以更适用于对实时性有强需求的系统.

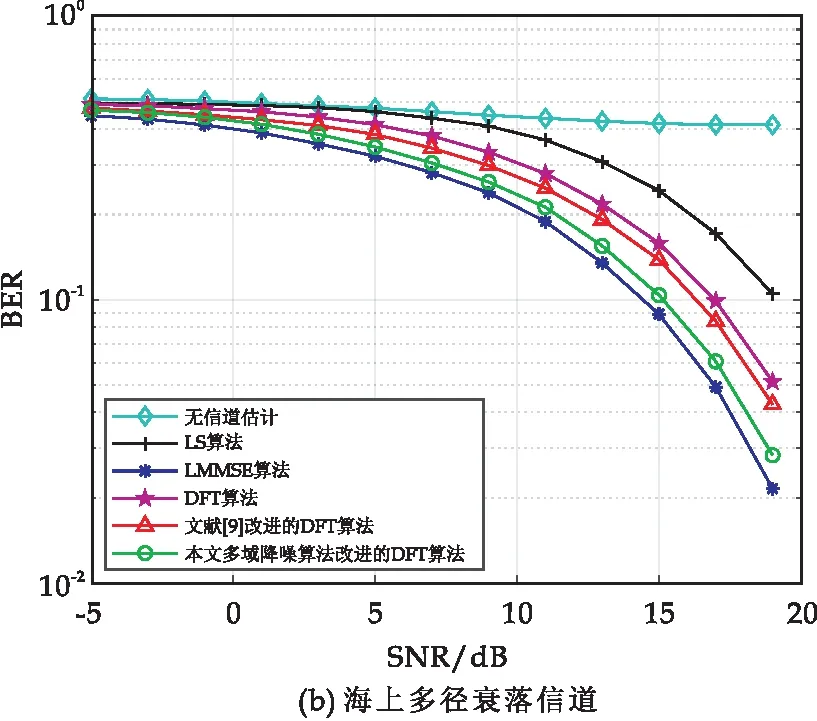
图9 不同信道下各算法的误码率比较

4 结论

噪声问题一直是困扰海上通信领域的难点,本文以传统DFT信道估计算法为基础,提出一种改进算法,该算法可改善传统算法中存在的噪声缺陷问题,改进算法通过将频域小波包去噪技术、时域阈值点优选以及变换域去噪相结合以过滤噪声,仿真结果表明,与几种经典信道估计算法和参考文献算法相比,改进算法性能更好,可得到精确的信道信息,且因其复杂度低实现比较简单,有很好的实际应用价值.