聚丙烯酸酯共聚物自愈合性能的分子动力学模拟

周建华, 李 楠, 刘秀青, 李 红, 刘 瑛

(1.陕西科技大学 轻工科学与工程学院 轻化工程国家级实验教学示范中心, 陕西 西安 710021; 2.陕西科技大学 前沿科学与技术转移研究院, 陕西 西安 710021)

0 引言

高分子聚合物在加工使用过程中,由于外力作用,会在材料的表面形成划痕或微裂纹,随着划痕和裂纹的扩散不但会降低高分子材料的性能,还会缩短材料的使用寿命[1].自发修复损伤的能力是自然界中一个重要的生存特征,因此模拟生物体损伤自修复机理的自修复高分子材料应运而生.自修复材料能够对细微的损伤进行自我修复,从而提高材料的安全性与使用寿命[2].近年来,关于利用自修复技术提高高分子材料性能的研究已经有了很多报道,已在涂料[3]、仿生材料[4]、传感器[5]和医用水凝胶[6]等领域得到了应用和发展.

目前,按修复机理划分,自修复材料主要包括外援型自修复材料和本征型自修复材料.与外援型自修复材料相比,本征型自修复材料主要依靠材料内部的非共价键相互作用或动态共价键来实现其修复性能,具有设计灵活、技术难度低和受损部位可重复修复的优点.共价键实现自修复通常需要外界刺激(光、热、催化剂)来促进自我修复,而非共价键可以在不需要任何外界刺激下快速自我修复,且修复率较高[7].自修复聚合物中的非共价键有氢键、范德华力、离子相互作用、金属-配体相互作用等,而氢键因为广泛存在于强极性基团之间,成键能低,常被用于实现自愈.Urban等[8]研究发现,范德华力广泛存在于聚合物中,因此基于氢键的聚合物材料的自愈合也可能是由范德华力驱动的.

然而,由于范德华力的存在和动态变化难以从实验上证实,计算机模拟的发展为研究范德华力提供了一种新途径.分子动力学模拟技术可以在原子尺度上研究聚合物的微观分子结构,揭示聚合物的内在机理,因此可以通过分子动力学模拟来研究材料的自愈性能.Chen等[9]合成了一种自愈聚氨酯材料,结合分子动力学模拟,提出了氢键与范德华力愈合机理的相互作用.结果表明,温度是影响氢键和范德华力的关键因素.He等[10]采用分子动力学方法建立沥青粘结剂的裂纹分子模型,研究了沥青粘结剂的自愈合行为.结果表明,沥青粘结剂内部真空微裂纹消失实现自愈合的主要原因是基于非键合分子之间的范德华力.

本文采用分子动力学模拟方法构建MMA-BA共聚物微裂纹模型,研究MMA与BA配比和愈合温度对MMA-BA共聚物自愈合行为的影响,通过密度、均方位移和扩散系数对自愈合行为进行分析,并对模拟结果进行验证.

1 模型建立

1.1 MMA-BA共聚物模型

利用MS软件进行分子动力学模拟.根据分子结构使用“Visualizer”模块绘制了MMA、BA单体分子模型(图1).首先构建聚合度为20的MMA-BA共聚物链(图2),其中MMA与BA摩尔比为3∶7、4∶6、5∶5和6∶4,然后放入16条MMA-BA共聚物链构建具有三维周期性边界条件及初始密度为0.1 g/cm3的无定型模型来模拟MMA-BA共聚物(图2).

图1 MMA和BA的分子模型

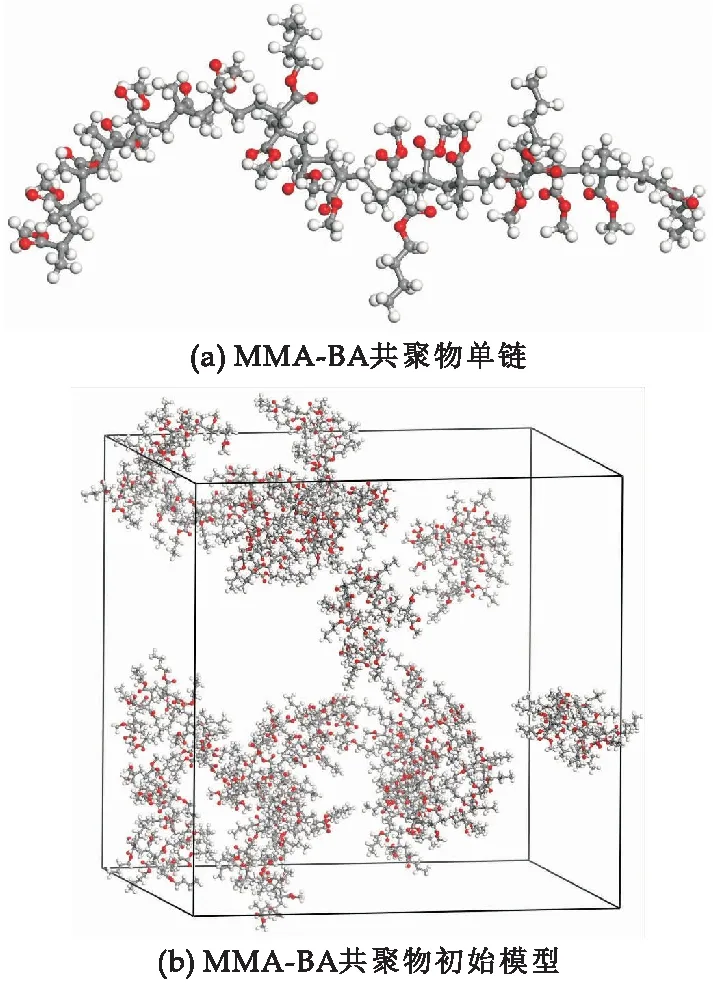
图2 MMA-BA共聚物单链和初始模型

在COMPASS[11,12]力场下,对建立的MMA-BA共聚物模型进行几何优化,退火处理,使体系空间达到最优化.在等温等体积(NVT)系综和等温等压(NPT)系综下先后对优化后的结构进行了100 ps的动力学处理,最终得到平衡后稳定的MMA-BA共聚物模型.

1.2 MMA-BA共聚物自愈合模型

为研究MMA-BA共聚物的自修复行为,通过Visualizer模块下的“Build Layer”命令工具,在25℃下,构建MMA-BA共聚物的微裂纹模型,将MMA-BA共聚物平衡模型放置于无定型晶胞中,在其中间添加一个20 Å的真空层,用来模拟损伤后的裂纹,如图3所示.通过Ewald和Atom based模拟方法[13,14]对平衡后的MMA-BA微裂纹模型的静电相互作用和范德华力进行计算.

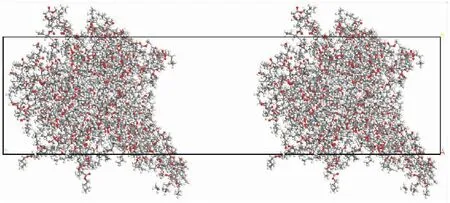
图3 MMA-BA共聚物微裂纹模型

2 结果与讨论

MMA-BA共聚物微裂纹模型的自愈合是分子在裂纹表面上移动重排的过程[15],可分为裂纹表面游离、分子向裂纹扩散以及愈合完成3个阶段,以此消除材料的不连续性并恢复材料性能[16],并且在自愈合过程中会受到温度和MMA与BA配比的影响,造成愈合程度的不同.

2.1 MMA-BA共聚物微裂纹模型的密度

密度是模型体积随时间变化最直观的基础数据,能直接反映模型的愈合过程.分别在25 ℃、50 ℃和75 ℃,NPT系综下对不同配比的MMA-BA共聚物微裂纹模型进行800 ps的分子动力学模拟.当MMA-BA共聚物微裂纹模型的密度在平衡密度1.02 g/cm3左右时,说明MMA-BA共聚物微裂纹模型的裂纹消失,愈合情况较好.由图4可知,在75 ℃时,MMA-BA共聚物微裂纹模型达到平衡的时间最短,且4种MMA与BA配比下MMA-BA共聚物微裂纹模型的密度均达到平衡密度,说明在该温度下,4种配比的MMA-BA共聚物微裂纹模型均实现了自愈合.在25 ℃和50 ℃时,当MMA与BA配比为5∶5时,MMA-BA共聚物微裂纹模型的密度达到了平衡密度,其他3种配比下均未愈合.由此说明,温度的升高对MMA-BA共聚物微裂纹模型的裂纹愈合有促进作用.

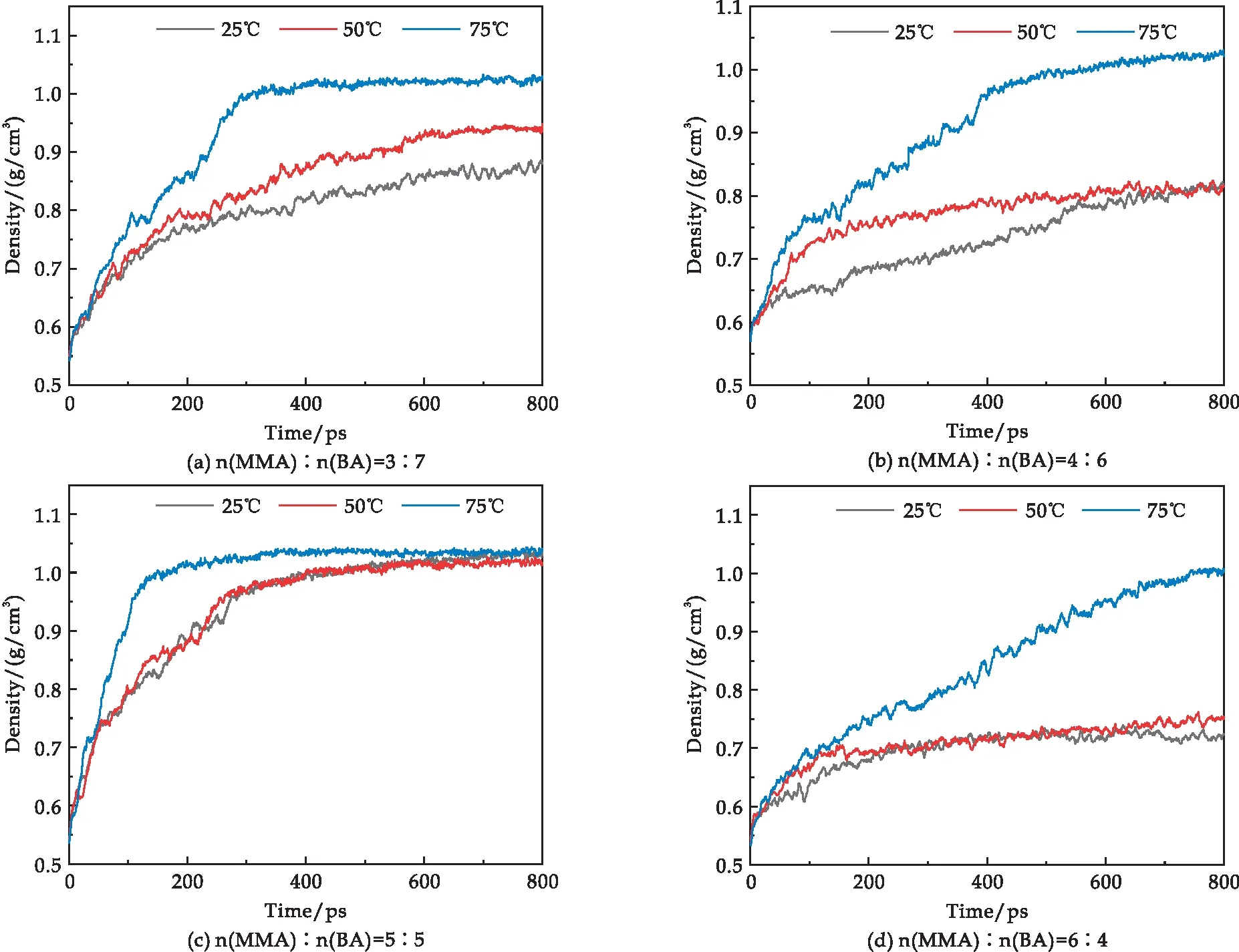
图4 MMA-BA共聚物微裂纹模型的密度变化

还可以看出,当n(MMA)∶n(BA)比值为5∶5时,MMA-BA共聚物微裂纹模型的愈合潜力最大.这是由于当n(MMA)∶n(BA)比值大于5∶5时,即硬单体MMA含量的较高,共聚物的硬度和内聚力较大,影响分子链的运动,使得共聚物微裂纹的密度达到平衡的速度变慢,愈合潜力降低.当n(MMA)∶n(BA)比值小于5∶5时,软单体BA含量较多,使分子链容易缠绕,运动能力降低,因此愈合潜力下降.

2.2 均方位移、扩散系数和相互作用

均方位移(MSD)是指体系内t时刻下所有原子的位移平方和的均值.粒子的运动可以近似看作随机游走,MSD可以用来判断体系是否平衡,MSD值随着模拟时间的增加而增加,当体系内的所有粒子达到平衡状态后而趋于稳定[17].均方位移的表达式如式(1)所示:

(1)

式(1)中:MSD为均方位移;ri(t)为t时刻原子位移;ri(0)为原子起始位移;N为原子数量.

原子扩散系数(D)表征粒子扩散快慢,通过扩散系数-温度曲线,得到温度对MMA-BA共聚物自愈合性能的影响.原子扩散系数表达式如式(2)所示:

(2)

式(2)中:D为原子扩散系数;ri(t)为t时刻原子位移;ri(0)为原子起始位移;N为原子数量.

在25 ℃、50 ℃和75 ℃下,通过分子动力学模拟对MMA-BA共聚物微裂纹模型的MSD进行了计算,如图5所示.由图可知,MSD曲线随时间的变化可分为三个阶段,最初斜率较大,逐渐减小后趋于平缓,并保持较长时间,最后斜率继续增加.这3个阶段分别对应了分子自由扩散(两层分子相互吸引,但并未接触)、逐渐接触且裂纹逐渐愈合和愈合后的分子稳定热运动.还可以看出,MSD随着温度的增加而增加.

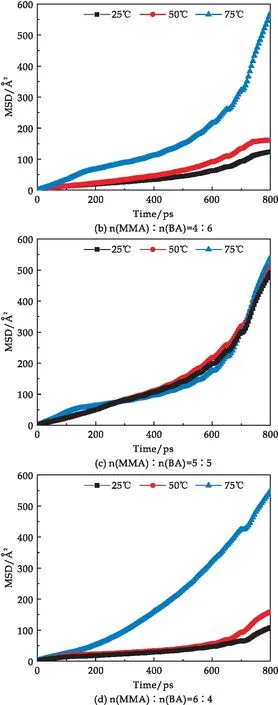
图5 MMA-BA共聚物的微裂纹模型的MSD变化

第一阶段的扩散可以用来评价体系的自愈合能力,计算出扩散系数,如图6所示.由图可知,不同配比下MMA-BA共聚物微裂纹模型的扩散系数都随着温度的升高而升高,当n(MMA)∶n(BA)为3∶7时,扩散系数从0.23增加到0.49;当n(MMA)∶n(BA)为4∶6时,扩散系数从0.13增加到0.43;当n(MMA)∶n(BA)为5∶5时,扩散系数从0.41增加到0.52;当n(MMA)∶n(BA)为6∶4时,扩散系数从0.10增加到0.41.这是由于温度越高,MMA-BA共聚物分子的扩散能力越大,分子的扩散运动越快,因此扩散系数增大.

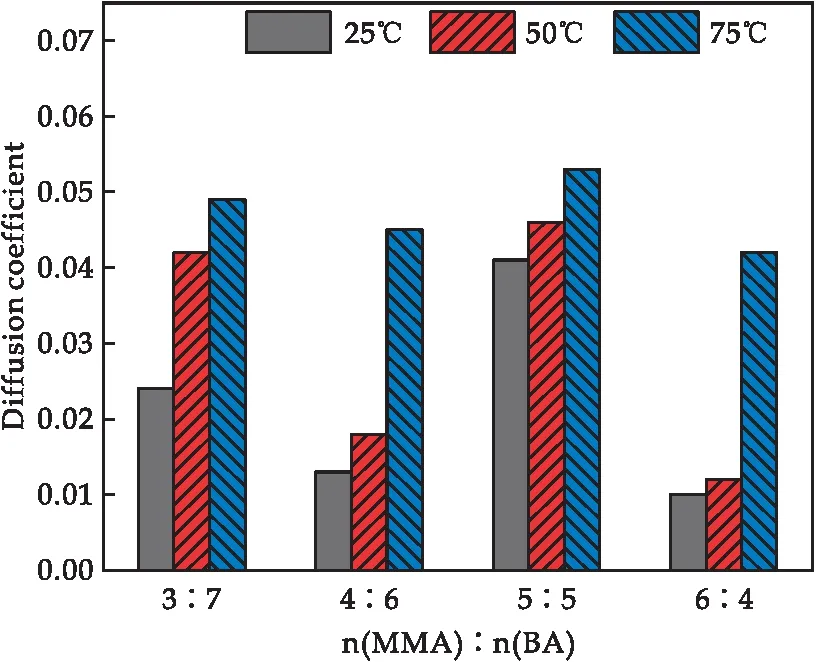
图6 MMA-BA共聚物微裂纹模型的扩散系数

以75℃下4种配比下的MMA-BA共聚物微裂纹模型为例,表1为MMA-BA共聚物微裂纹模型的范德华力(EvdW)和静电相互作用(Eelec).由表可知,负值的范德华力表明分子相互吸引[18],范德华力的贡献大于静电相互作用,说明范德华力在MMA-BA共聚物自愈过程中起着重要的作用.

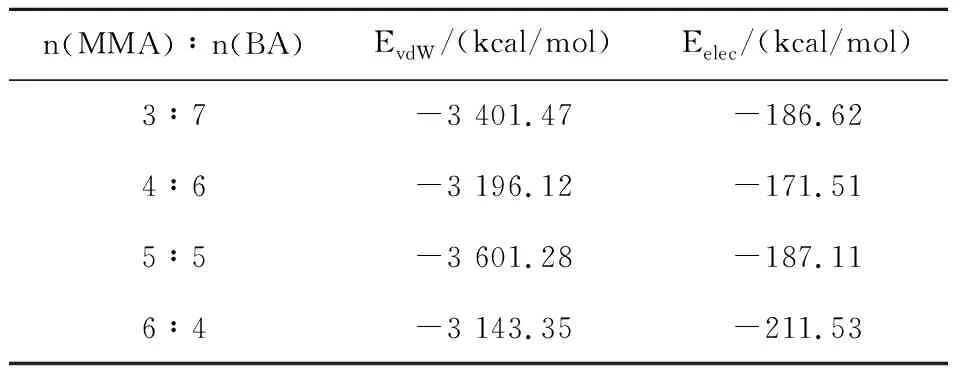
表1 MMA-BA共聚物微裂纹模型中能量随温度的变化

2.3 MMA-BA共聚物微裂纹模型的力学性能

分别计算了在75 ℃下MMA-BA共聚物模型的力学性能及经过800 ps分子动力学模拟计算后MMA-BA共聚物微裂纹模型的力学性能.通过比较愈合前后的杨氏模量和体积模量来衡量MMA-BA共聚物的自愈合效率.

MMA-BA共聚物自愈合前后的力学性能及自愈合效率如图7所示.由图可知,自愈合前后的杨氏模量和体积模量都随着n(MMA)∶n(BA)比值的增大而增大,这是由于MMA是硬单体,其含量增加,会使得聚合物的内聚力增大,乳胶膜的硬度和强度增大,因此MMA-BA共聚物的力学性能不断提高.还可以看出,当n(MMA)∶n(BA)比值为5∶5时,MMA-BA共聚物微裂纹模型的力学性能自修复效率最好.

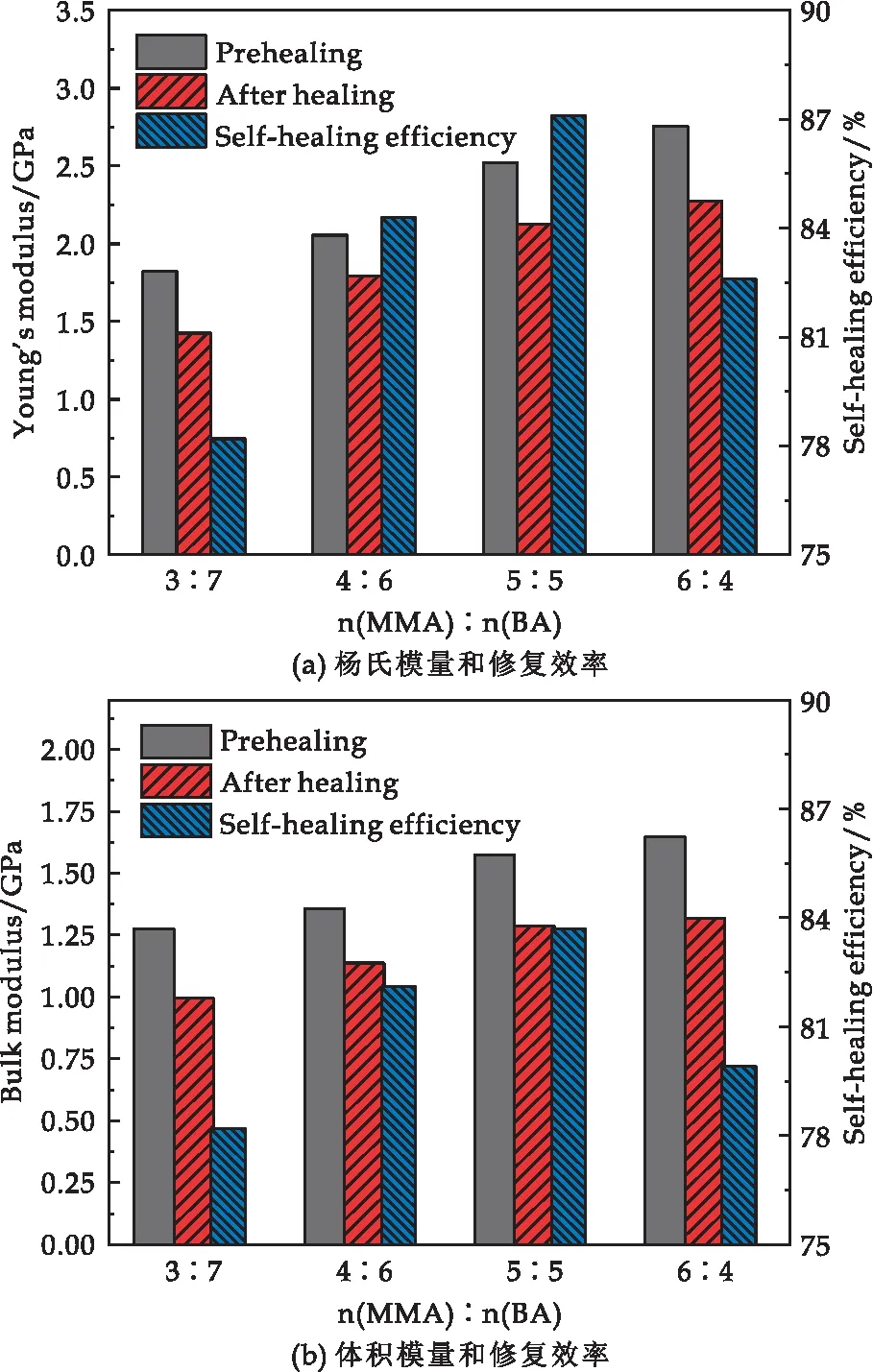
图7 MMA-BA共聚物修复前后力学性能和修复效率

3 实验验证

为了评价分子动力学模拟MMA-BA共聚物自修复性能的可靠性,对MMA-BA共聚物膜的自修复性能进行了实验验证.按照课题组前期建立的方法[19]制备MMA-BA共聚物乳液.将乳液在室温下成膜,并放入60℃烘箱中充分干燥,得到MMA-BA共聚物膜.将样品贴在玻璃片上,用手术刀在表面划出伤口,然后将带有划痕的样品放入75℃的烘箱中保温7 h,用超景深显微镜观察样品划痕前后的变化.

图8为MMA与BA配比对MMA-BA共聚物乳胶膜自修复性能的影响.由图可知,4种配比的MMA-BA共聚物乳胶膜在加热条件下,其划痕都有变窄,当n(MMA)∶n(BA)比值为5∶5时,乳胶膜上的划痕几乎消失,愈合能力最好.这是由于当n(MMA)∶n(BA)比值小于5∶5时,聚合物链中的软链段PBA较长,导致分子链缠连,使分子链的运动能力降低;当n(MMA)∶n(BA)比值大于5∶5时,聚合物中的硬链段PMMA较长,导致共聚物刚性变强,因此分子链运动能力下降,使得愈合效果变差.由上述数据可知,实验结果与模拟结果基本一致,当n(MMA)∶n(BA)为5∶5时,MMA-BA共聚物的自修复性能最好,由此表明,分子动力学模拟可以用来预测MMA-BA共聚物的自修复行为.

图8 n(MMA)∶n(BA)比值对乳胶膜自修复性能的影响

4 结论

本文采用分子动力学方法研究了MMA与BA摩尔比为3∶7、4∶6、5∶5和6∶4时,MMA-BA共聚物微裂纹模型在25 ℃、50 ℃和75 ℃下的自愈合行为.通过密度、均方位移、扩散系数和力学性能评价了MMA-BA共聚物模型的自愈合性能,并对MMA-BA共聚物乳胶膜进行了实验验证.最终,得出以下结论:

(1)MMA-BA共聚物微裂纹模型的自修复行为受温度和MMA与BA配比的影响.当温度升高时,MMA-BA共聚物微裂纹模型的愈合潜力变大.当MMA与BA摩尔比为5∶5时,MMA-BA共聚物微裂纹模型的裂纹愈合最好.

(2)MMA-BA共聚物的力学性能会随着MMA用量的增多而增强.当MMA与BA摩尔比为5∶5时,MMA-BA共聚物微裂纹模型的自修复效率最高.

(3)实验结果与模拟结果基本一致,说明分子动力学模拟可以较准确地预测MMA-BA共聚物的自修复行为.