CFD-BP 神经网络耦合算法对焚烧炉的一次风管道配风的模拟研究
2023-12-05周洪权陈德珍尹丽洁戴小云陆子叶
周洪权,陈德珍,尹丽洁,张 智,戴小云,陆子叶
(1.同济大学热能与环境工程研究所,上海 200092;2.上海环境卫生工程设计院有限公司,上海,200232)
1 引言
随着国民经济高速发展,城市生活垃圾产量逐年增长,2021 年我国城市生活垃圾清运量为2.49 亿t,无害化处理率为99.9%,其中焚烧无害化处理量为1.80亿t,占无害化处理量的72.4%[1-2]。“十四五”规划提出,到2025年底,全国城镇生活垃圾焚烧处理能力达到80万t/d左右,远大于目前中国城镇生活垃圾无害化处理能力[3]。随着垃圾分类收运、分类处理的推行,焚烧炉炉前垃圾的水分降低、热值升高[4],垃圾理化特性的改变使得现有焚烧炉在运行过程中的负荷、风量等需要进行相应的优化调整[5]。
炉排式焚烧炉由于物料预处理简单、单台处理量大、炉渣体积小等特点,是我国生活垃圾焚烧炉中应用最多的炉型[6]。目前对炉排式焚烧炉研究多采用炉排上产物预测+燃烧室内气相燃烧的方式,燃烧室内的烟气温度、成分等取决于炉排上产物的预测。实际炉排上产物的成分与含量除了受燃烧室高温烟气的影响外,还与一次风分配密切相关。
炉排式焚烧炉的一次风通常由炉排下方向上吹送,经过燃料床层后进入炉膛内部,一次风除了能为料层的固相燃烧提供氧气之外,还具有干燥垃圾、析出挥发份、使料层稳定着火以及冷却炉排的作用。垃圾焚烧炉一次风布置方式大多为母管制,从每段炉排的一次风母管进行分支,通过分支管路将一次风送到炉排下部风室,运行过程中通过调节阀门,改变一次风入炉量,从而改变燃烧状况。单个母管上通常连结3~9个支管,每个支管上装有风量调节阀门,由于整个一次风系统是连通的,单个支管的风量调节影响所有支管出口的风量分配。随着生活垃圾焚烧炉逐渐大型化,炉膛宽度逐渐变宽,燃烧区域面积变大,受母管制布风结构的限制,对于区域化燃烧状况调整影响较大,调整也异常艰难[7-8]。一般管路配风设计都是基于经验参数方法,查询沿程阻力系数和局部阻力系数,来进行复杂管路系统的配风设计计算,目前尚没有普适的经验公式能够预测不同阀门开度时单个支管风量的变化对整个一次风管道配风的影响。
随着数值模拟模型的完善和计算机性能的提升,通过数值模拟的方法可以预测不同阀门开度时各个支管出口的风量。巴海涛等[9]采用数值模拟的方法研究了船舶风管中的空气流动,调整了风管走向及出口,改善了机舱风管的风量分配。王淑坤等[10]通过模拟汽车的空调风道,改善了各出风口的风量分配情况。Kumar等[11]通过数值模拟方法研究了在不同通风条件下纺织品蒸制过程中的风速与温度情况,给出了通风优化的建议。Zhao 等[12]通过数值模拟卫星发射前清洁存放循环风空调系统喷射方式,研究了在不同卫星布置下循环风量的控制策略,为减小循环风量提供了一种可行方法。
由于炉排式焚烧炉一次风管道系统的支管数量多,调节某一支管的阀门开度时,都需要重新计算,并且某一支管阀门开度的改变影响所有支管出口的流量分配,风管阀门开度与它们各自的出口风量是一个多变量互相耦合的关系,仅通过数值模拟很难寻到最优工况。BP(back propagation)神经网络是一种按照误差逆向传播算法训练的多层前馈神经网络,是实现机器学习的主要算法之一[13]。如图1所示,BP神经网络基于现场多维的离散数据,通过卡方检验的方法对数据降维处理,通过反向传播不断调整网络的权值和阈值,使网络的误差平方和最小[14]。神经网络模型发展多变量非线性相关关系的度量来寻求与其他数据之间的函数关系,随着数据量的增加函数关系也会变得越来越复杂,未来对于数据的预测也会越来越准确。
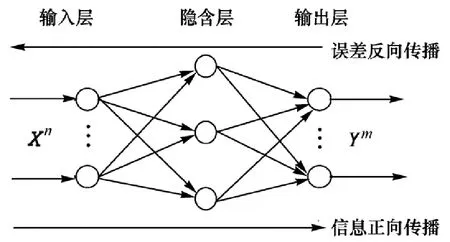
图1 BP神经网络示意图Fig.1 Schematic diagram of BP neural network
神经网络模型可以克服CFD建模时多变量互相耦合、互相影响的问题,可以提高预测效率。景亮等[15]建立了出菇房温度CFD模型,引入温度均匀性指标,通过CFD模拟得到不同工况下的模拟数据,并将这些数据作为神经网络的样本数据,训练神经网络模型以预测出菇房的温度均匀性指标。杨磊磊等[16]利用数值模拟方法获得了压力容器中的温度场分布,并基于数值模拟结果建立了BP神经网络模型进行温度预测。Mukesh等[17]利用双流体模型对循环流化床中轴向固含率分布进行计算,并基于数值模拟结果建立数据集训练神经网络模型对固含率进行预测。神经网络的对象是数据,在诸多相互关联的数据中,仅仅靠人工筛选和学习,很难发现数据对结果的影响。神经网络通过采集CFD 模拟得到的数据,积累历史数据,使用大量的数据来训练模型,可在后续的计算中替代CFD模拟,降低CFD模拟的计算量。
本研究中首先根据实际一次风管尺寸建立计算模型,通过CFD 的数值模拟得到不同支管上阀门不同开度时的出口流量分配结果并建立数据集,选取部分数据作为训练样本,其余数据作为测试集,然后使用BP 神经网络模型建立焚烧炉一次风风量分配预测模型并以结果的均方误差评估,实现理想情况风量分配下各个支管的阀门开度的预测。
2 计算模型及数据处理
2.1 CFD计算模型
研究对象为500 t/d 的生活垃圾焚烧炉一次风分配管道,计算模型如图2所示,一次风由总管进入3 个支路,其中干燥段和燃烧Ⅰ段在第1 支路上,燃烧Ⅱ-1 段在第2 支路上,燃烧Ⅱ-2 段和燃烬段在第3 支路上。炉排深度方向按照三列布置,每列的干燥段下有一个配风仓室,每列燃烧Ⅱ-1和燃烧Ⅱ-1段下各有两个配风仓室,每列燃烬段下有一个配风仓室,每个仓室由3个支路引出通过支管连接,共计18个支管。计算模型如图2所示,采用六面体网格,网格数约为131万。主要模型参数见表1。
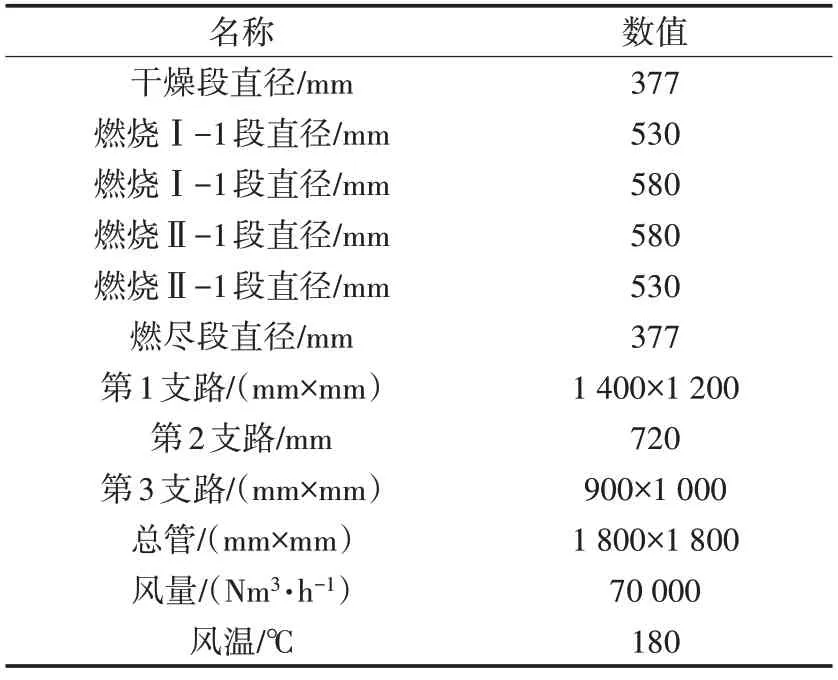
表1 主要模型参数Tab.1 Main model parameters
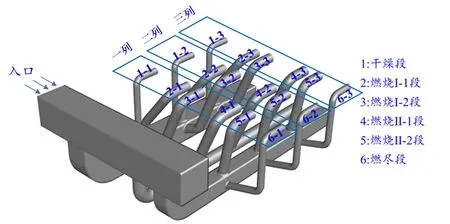
图2 计算模型Fig.2 Schematic diagram of geometric model
2.2 控制方程
计算过程中假定整个一次风系统中气体温度恒定,气相控制方程主要包括质量守恒方程和动量守恒方程。
气相质量守恒方程:
式中:ρ为气相的密度,单位为kg/m3;u为速度矢量,单位为m/s。
气相动量守恒方程:
式中:ρ为压力;i、j为坐标系中的方向;g为重力的分量,单位为m/s2;Fi为阻力等其他源项;μ为流体的粘度,单位为kg·m-1·s-1。
采用k-ε 模型求解湍流的影响,其中湍动能k和耗散率ε方程如下:
式中:GK是速度梯度产生的湍动能;Gb为浮力作用产生的湍流动能;YM为可压缩湍流中的脉动扩张;G1ε、G2ε为系数;Sε为源项。
2.3 边界条件
采用三维稳态模型,选择Coupled 模型计算压力与速度之间的耦合。设定气体入口为流量入口边界条件,出口为压力出口边界条件,壁面为无滑移绝热边界条件。
阀门开度是调节风量的重要参数,阀门开度实际影响的是管道的流通面积,在模拟过程种,通过在管道中设置挡板调节管道的流通面积,计算不同阀门开度的影响。
2.4 BP神经网络模型
2.4.1 BP神经网络模型的建立
神经网络中隐含层的神经节点数与BP 神经网络的非线性映射能力呈正相关关系,网络结构设置影响预测结果的准确程度[18]。与单个隐含层数量相比,拥有两个及以上隐含层单元数的BP神经网络结构在进行训练测试时更容易出现局部极值,本研究选用单一隐含层的三层BP 神经网络,输入层共18 个节点,分别为18 个支管出口的风量,输出层同样为18个节点,分别为18个出口对应的阀门开度。
隐含层神经元是完成从输入层神经元到输出层神经元非线性映射的关键。若隐层节点数太少,网络可能根本不能训练或网络性能很差;若隐层节点数太多,增加隐藏层中神经元的数量也并不意味着模型将具有更好的预测精度[19],一方面使网络训练时间延长,另一方面,训练容易陷入局部极值而得不到最优点,也是在神经网络训练时出现“过拟合”的内在原因。公式(5)[20]给出了隐含层节点数的计算方法:
式中:m和n分别为输入层和输出层的节点个数;a的取值范围为[1,10]。根据输入层神经元个数是18,输出层神经元的个数是18,可得神经网络模型隐含层节点数为[7,16]。本研究从7 个节点开始,再分别增加至16 个来测量不同数量的节点数对模型误差的影响,最后选择均方误差最小的数量作为隐含层节点数,均方误差公式为:
式中:n为训练样本数量;f(xi)为原始数据集中输出数据,yi为训练后输出数据。
训练函数选择Levenberg-Marquardt(trainlm 训练函数),学习率为0.01,迭代次数设为1 000,误差阈值设为0.001。使用平均绝对误差(MAE)和决定系数(R2)来评估所建立的神经网络性能,公式如下:
式中:Yi为原始数据集中输出数据,为训练后输出数据,为原始数据集中输出数据平均值,n为数据数量。
2.4.2 数据预处理
在数据集构建过程中,设置了不同支路上阀门的不同开度,通过统计不同阀门开度下各个出口处的风量,计算炉排不同段的风量分配比例,共获得了65 条数据,其中70%作为训练集,30%作为测试集。由于原始样本中各向量的数量级差别很大,为方便计算并防止部分神经元达到过饱和状态,对训练集数据进行了归一化处理。本文采用MATLAB R2021a的内置函数mapminman 函数对数据进行归一化处理,将数据归一化到[0,1],归一化函数公式为:
式中:y为输出值,x为所选数据,xmax、xmin为数据集中最大值、最小值,ymax、ymin为1、0。
3 结果与分析
3.1 CFD模拟结果
由于不同炉排段上的出口3 离入口较远,受网格影响大,所以采用出口3 处的风量比例验证网格质量。图3 给出了网格数分别为约7 万、34 万、131万和413 万时的不同炉排段出口3 处的风量比例,可以看出网格数为7 万和34 万时,出口处的风量比例与网格数为413 万相差较大,网格数为131 万时,出口处的风量与网格数为413 万时相近,为了提高计算效率,模拟过程中采用131的网格进行计算。
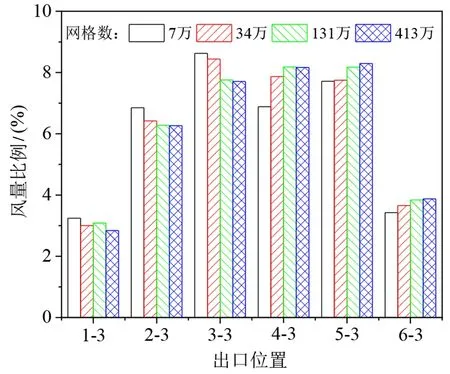
图3 不同网格数的出口风量分配Fig.3 Distribution of air flow at the outlet with different grids
图4给出了阀门全开时一次风系统的速度矢量图。从图中可以看出,3个支路管内的速度分布并不均匀,由于气流的惯性,3个支路气流都会吹到管路的右侧壁面,再沿壁面反射回来,形成类似旋转的气流形式。18个支管内速度分布也不均匀,与3个支路管道类似,气流会吹到沿流动方向对面的管壁上,其中干燥段和燃烧Ⅱ-1段的支管内速度不均匀性较大。
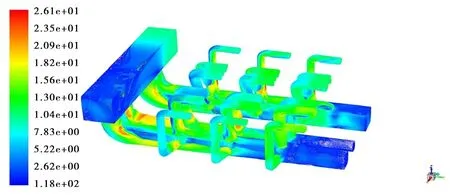
图4 气体速度矢量图Fig.4 Gas velocity distribution
图5 分别给出了阀门全开和干燥段阀门开度93.3%时不同炉排段的风量分配。阀门全开时6 个炉排段的风量分配分别约为8.4%、17.7%、23.2%、19.0%、21.7%、10.0%。其中第4支路的管径较细,阻力大,造成燃烧Ⅱ-1 段的风量较低。图中同时给出了现场运行时的风量分配,现场运行时各支管的风量与阀门开度见表2。
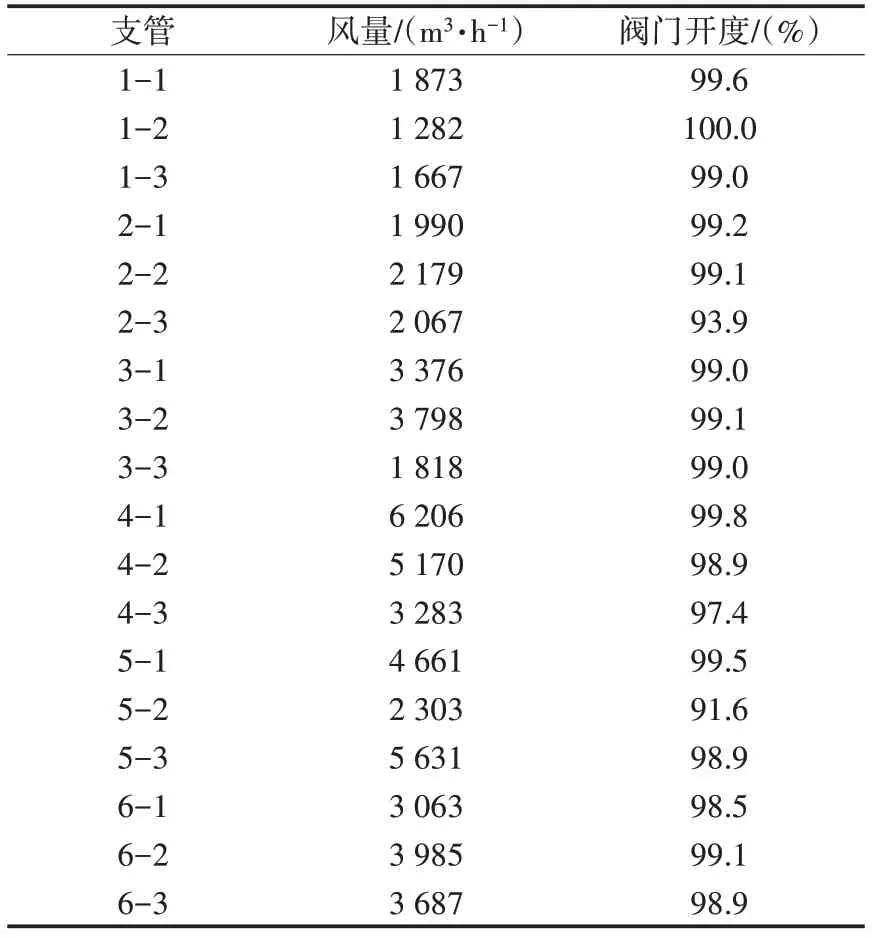
表2 现场运行时各支管风量及阀门开度Tab.2 Actual values of air volume and valve opening of each branch pipe
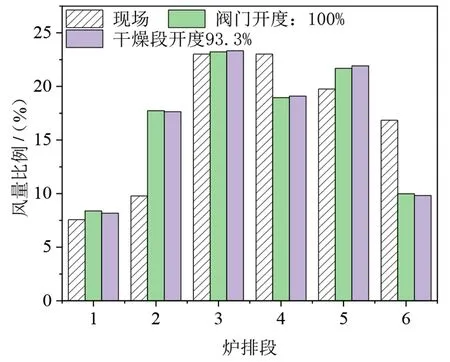
图5 不同段的炉排风量分配Fig.5 Air volume distribution of different grate sections
模拟计算得到的风量分配与现场总体趋势一致,风量集中在燃烧段。由于现场运行时炉排上堆积了料层,不同燃烧段料层的厚度和料层的孔隙度不同,同时现场运行时各阀门的开度根据炉排上垃圾料层厚度和推料速度调节有所不同,因此各个支管的风量分配比例不尽相同,表2中的数据为现场运行时DCS 上实际数据。当干燥段开度设为93.3%时,干燥段风量相对减少,其余支路的风量有不同程度的变化,这也说明焚烧炉一次风管道配风模型t各支路之间存在着耦合关系,是一个多变量互相影响的过程,当改变一个支管的阀门开度时,其余支管的出口风量都将产生变化,若想得到理想配风比的情况,仅仅靠CFD模拟需要消耗大量的计算时间。
3.2 神经网络预测结果
不同隐含层神经元数量得到的训练结果均方误差如图6所示,从图中可以看出,随着隐含层节点数的增多,训练结果均方误差呈先下降后升高的趋势,隐含层神经元个数为13 时BP 神经网络对函数的逼近效果最好,故本研究将网络的隐含层神经元数目定为13。
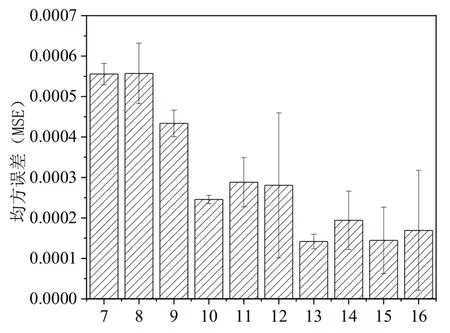
图6 不同隐含层神经元数量训练结果均方误差Fig.6 Mean square error values of different training results
将测试集样本的输入数据进行归一化处理,并将测试集的输出数据代入已训练完的网络中进行仿真测试,即利用MATLAB R2021a 中的simulink 仿真测试函数将测试集样本数据录入进BP 神经网络当中然后再经过reverse 反归一化函数把得出的预期结果输出数据反归一化来实现仿真测试。根据图7所示,BP神经网络在完成了14次训练好已经达到了稳定状态,且满足了误差阈值为0.001 的条件,最佳验证性能为第8轮的训练。
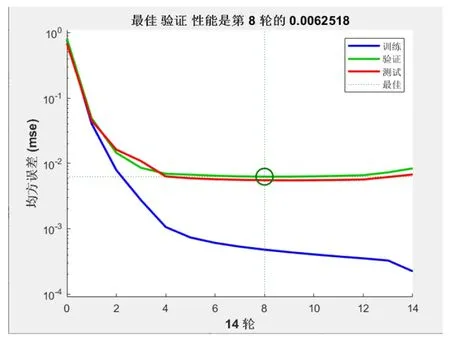
图7 BP神经网络训练结果及训练次数Fig.7 BP neural network training results and training times
仿真测试集样本数据在测试完成时模型的训练结果对比和解释度分别如图8和图9所示,可以看出基于BP 神经网络的一次风系统分配预测模型的解释度R=0.98724,说明仿真测试的预测结果与其实际值间的相关程度高,这也表明模型的训练是准确的。
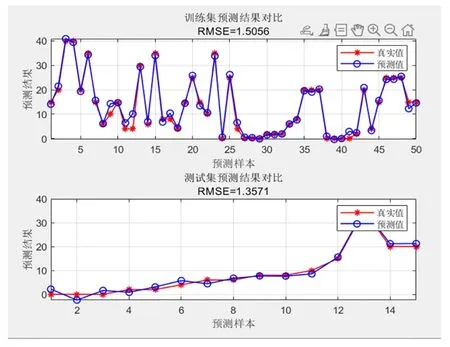
图8 测试完成时模型的训练结果对比Fig.8 Comparison of training results of models
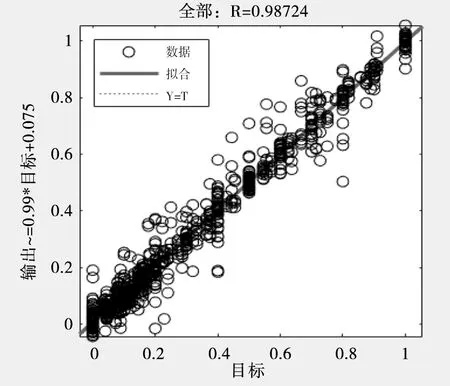
图9 测试完成时模型的解释度Fig.9 The interpretability of the model
仿真测试集样本数据在测试完成时训练集与测试集的平均绝对误差和决定系数分别如图10 和图11 所示,在进行多次重复训练后,训练集与测试集的平均相对误差分别约为1.24%和2.01%,训练集与测试集的平均相对误差分别最低达到了0.83%和1.49%。训练集与测试集的决定系数分别约为0.98 和0.91,训练集与测试集的决定系数分别最高达到了0.988和0.981,这也表明训练质量较高,模型能较好表现出数据之间的非线性映射关系,所建立的神经网络结构比较合适,网络可以较为准确地预测在理想配风比下各个出口的阀门开度。
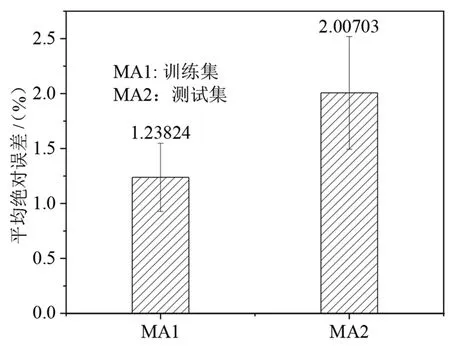
图10 训练集与测试集的平均绝对误差Fig.10 Average absolute error value between training and testing sets
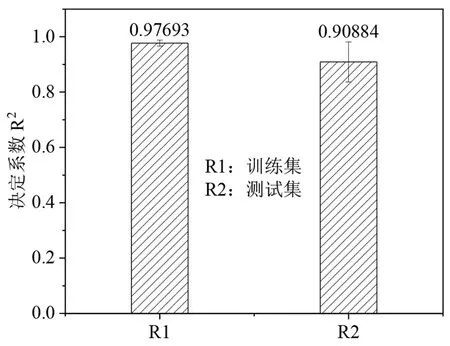
图11 训练集与测试集的决定系数Fig.11 Coefficient of determination between training and testing sets
4 结论
本文提出了一种CFD-BP 耦合算法,基于CFD计算得到一次风系统中各支管的风量分配,采用BP 算法预测不同支路阀门开度对整体管路配风的影响,该耦合算法可为建立智能配风设计与设备运行智能管理提供一定的理论支撑,主要结论如下:
(1)建立了某500 t/d 的生活垃圾焚烧炉一次风管道分配CFD 计算模型,计算了在不同阀门开度下各个支管出口的流量分配情况,并与实际结果进行了比对,模拟计算得到的风量分配与现场总体趋势一致。
(2)以CFD 计算结果为数据库,建立了以各个支管出口风量为输入量的一次风管道分配BP 神经网络模型,模型训练集与测试集的平均相对误差分别最低达到了0.83%和1.49%,训练集与测试集的决定系数分别最高达到了0.988 和0.981,预测效果较好。
