基于线结构光的钢领内表面圆度测量方法

金守峰, 沈文军 , 肖福礼, 李 毅

(1.西安工程大学 机电工程学院, 陕西 西安 710600; 2.西安工程大学 西安市现代智能纺织装备重点实验室,陕西 西安 710600; 3.陕西省计量科学研究院, 陕西 西安 710100)

钢领作为细纱机的关键零件,其内表面与钢丝圈形成运动副,完成纱线的加捻、卷绕等工艺,钢领内表面圆度的几何精度影响着纱线质量[1]。现有的钢领内表面圆度检测方法主要是人工接触式测量,其结果易受人为主观因素影响,测量效率不高,劳动强度较大。随着机器视觉技术的快速发展,国内外学者在机械零部件几何精度测量领域进行了深入研究。甘佳佳等[2]提出基于投影法的钢领圆度检测系统,采用LabVIEW软件实现了对钢领圆度的测量;金守峰等[3]提出基于Zernike矩边缘模型提取钢领内圈的亚像素边缘点,建立了基于图像信息的内圈圆度数学模型,实现钢领内圈圆度的非接触式测量;庞云龙等[4]对光纤端面图像进行预处理,提取边缘轮廓特征,建立了基于最小二乘椭圆拟合的纤芯和包端层面的圆度评价模型;金守峰等[5]提出基于改进的Zernike矩的回转类零件圆度视觉测量方法,建立轴截面圆度测量数学模型,实现了回转类零件直径与圆度的非接触式测量;Krantikumar等[6]利用图像处理技术对圆形零件进行圆度测量,解决了接触式测量时试样与测量探头之间的磨损问题;刘杰等[7]针对大尺寸筒状设备的圆度测量融合激光准直及图像处理技术,测量系统的精度达到0.7 mm;陈厚瑞等[8]利用测量显微镜CCD相机采集微球图像,通过梯度非极大值抑制迭代算法分割图像,提取微球轮廓后进行最小二乘圆拟合,得到了球的圆度参数;朱丹丹等[9]提出基于3σ准则和自适应滤波的盲孔圆度测量方法,建立圆度误差数学模型,实现盲孔的圆度误差测量;林强强等[10]通过建立工件旋转模型,对夹角图像进行旋转校正,采用Canny算子提取工件的边缘轮廓特征,得到被测工件的实际尺寸;马金钰等[11]提出基于激光位移传感器的圆径测量角度安装误差方法,解决了在圆径未知的情况下,激光位移传感器的角度安装误差的高精度测量问题;韩宗旺等[12]对单目相机获取的工件轮廓进行三维重构,通过基于最小包容区域原则的自适应搜索逼近法对短轴零件的轮廓坐标点进行圆度评定;杨姝等[13]针对列车车轮踏面不圆度检测问题,提出采用三点定位及导向轮反向设计,实现了列车车轮踏面不圆度的快速测量。

针对钢领内表面圆度在人工接触式测量中存在的主观干扰及自动化程度低等问题,本文提出基于线结构光的钢领内表面圆度测量方法,采用基于主成分分析的改进Steger方法提取线结构光条纹中线,重构钢领内表面,建立基于点云信息的钢领内表面圆度测量模型,以期实现钢领内表面圆度的非接触式测量。

1 钢领结构分析

钢领结构及示意图如图1所示,钢领在钢领座上定位安装,钢领压板压紧钢领的凸缘,采用螺钉固定在钢领板上,随钢领板进行升降运动。粗纱经过牵伸、导纱钩和钢丝圈进行卷绕和加捻。钢领内表面为光滑圆柱形的工作面,正截面为圆形,与钢丝圈形成配合,因此钢领内表面的圆度误差是重要的几何精度,影响着纱线的质量。FZ/T 92018—2021《平面钢领》中规定了钢领的圆度精度,用于控制内表面正截面的形状误差。

图1 钢领结构及其示意图Fig.1 Steel ring structure and schematic diagram.(a) Schematic diagram of steel ring installation structure; (b) Schematic diagram of steel ring

2 基于线结构光的钢领圆度测量系统

2.1 线结构光测量原理

线结构光测量原理如图2所示,激光器向被测物体发射激光,在空间形成一个激光平面,且与成像平面的投影连线相交于点P。由图像传感器获得图像,在标定板上建立世界坐标系,通过系统的几何关系计算得到点P的三维坐标[14]。采样点的三维重构光条中心的像素点p′c=(uc,vc),从像素坐标系转化到世界坐标系的方程为

图2 线结构光测量原理Fig.2 Principles of structured light measurement

(1)

式中:(uc,vc)为成像面中对应于图像坐标系中的像素坐标;K为相机的内参矩阵;R、T为相机的旋转矩阵和平移矢量;(Xw,Yw,Zw)为世界坐标系下的坐标值;f为相机内部参数;(u0,v0)为光条中心坐标。

世界坐标系下光平面的方程为

aXw+bYw+cZw+d=0

(2)

式中,a、b、c、d为光平面标定系数。

由式(1)、(2)可得P点的世界坐标:

(3)

由式(3)可知,在相机的内参矩阵K、旋转矩阵R、平移矢量T已知的前提下,可获得世界坐标系下点P的三维坐标。

如图2右侧局部放大图所示,设光点在图像平面上的变化位移为y,根据几何关系,则入射点的位移x为

(4)

式中:l为镜头到被测点的距离;d为镜头中心到相机像面的距离;α1为激光光轴与被测物体法线夹角;α2为相机光轴与被测物体法线夹角;β为像平面与相机光轴的夹角。

由于d>>y,β≈90°,则式(4)可简化为

(5)

设像面上单个像素的长为b1,像素个数为n,则图像平面上的变化位移y=nb1,将y代入式(5)可得

(6)

当n=1 时,此时的x为该检测系统的测量精度,参数l和d为系统固定参数。系统中α1±α2的数值越大,则系统检测精度越高。为降低钢领内表面的高光反射对图像质量的影响,确定α1+α2=45°,l=70 mm 时具有较好的成像质量。

2.2 基于线结构光的钢领圆度测量系统

2.2.1 测量系统的组成

根据线结构光测量原理构建了钢领内表面圆度测量系统,如图3所示。钢领装夹在三爪卡盘上,Arduino UNO为控制器,驱动步进电动机带动钢领旋转。线激光传感器为M-16A650-10-LS型传感器(650 mm、10 mV),维视MV-EM200 M-40fps相机,选配8 mm的定焦镜头,相机与钢领内表面的距离为70 mm,相机与线激光传感器的夹角为45°。

图3 钢领内表面圆度测量系统Fig.3 Ring roundness measuring system

2.2.2 相机标定

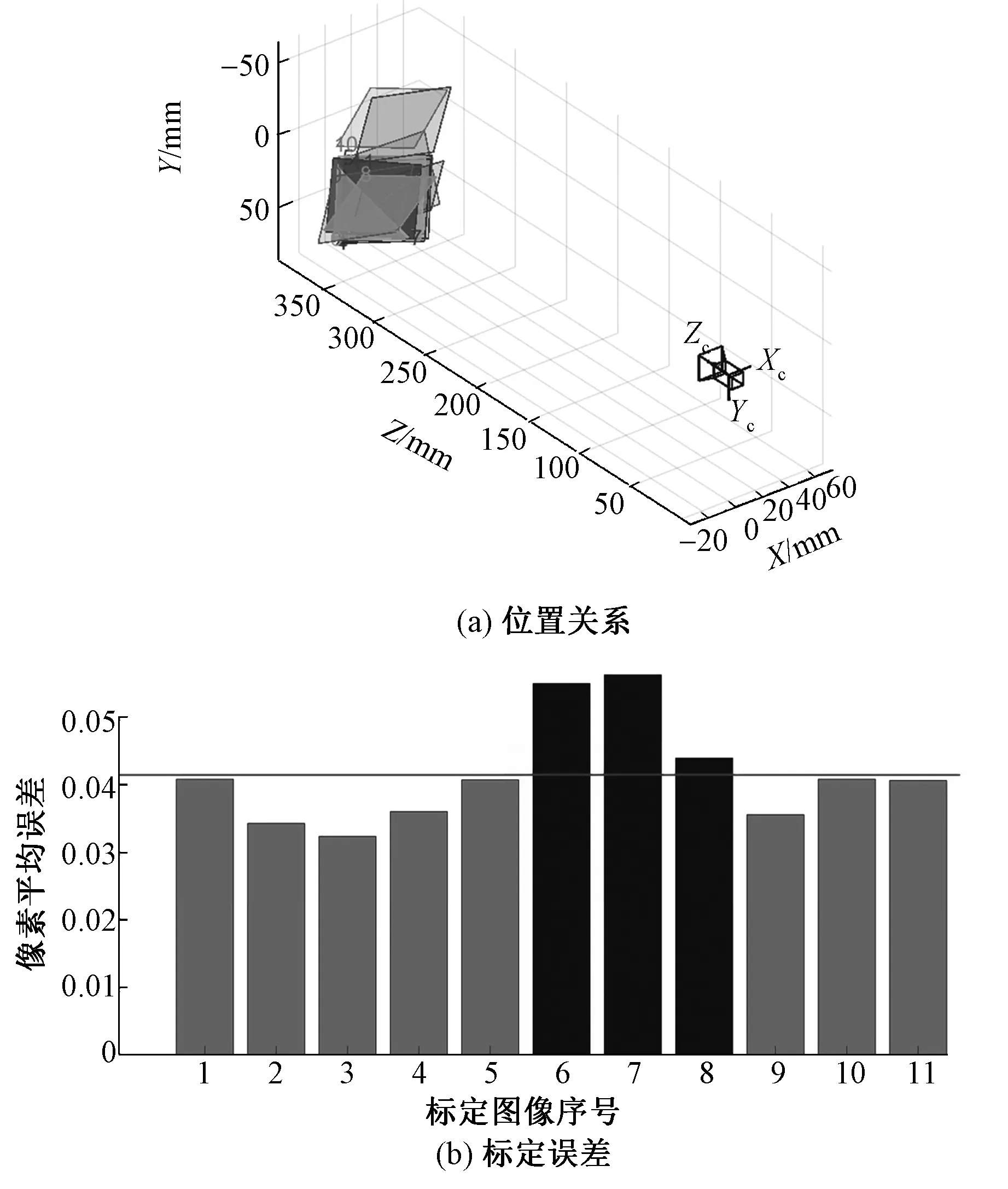
图4 相机标定Fig.4 Camera calibration.(a) Positional relationship; (b) Calibration error

2.2.3 光平面标定

获取到标定板上的线结构光条纹后,采用奇异值分解(SVD)分解L(L=UDVT)对光平面方程参数进行求解[15]。其中:U、V为酉矩阵;D为奇异值沿对角线从大到小构成的对角矩阵,D中最小奇异值在VT中对应的特征向量为式(2)中的系数。计算得到拟合的光平面方程:

0.355 8Xw-0.18Yw+0.97Zw-6.356 4=0

(7)

2.2.4 旋转轴标定

激光器相对于钢领内表面的位置固定不变,钢领随三爪卡盘在电动机的驱动下旋转。为得到世界坐标系的旋转轴方程,按图5所示将标定板固定在三爪卡盘上,标定板平面与三爪卡盘旋转轴重合。转动三爪卡盘,在不同的位置采集2张标定板图像[16]。标定板右上角第1个角点处为世界坐标系原点,Z轴垂直于靶面。

图5 旋转轴标定Fig.5 Calibrating axis of rotation

由于世界坐标系建立在标定板平面,则Zwj=0,由此得标定板的平面方程:

(8)

式中:j为标定板平面数;aj和Tj为外参数。

(9)

3 钢领圆度测量模型

3.1 钢领内表面线结构光条纹的特征提取

3.1.1 线结构光条纹感兴趣区域的获取

线结构光条纹为本文的感兴趣区域,大部分背景为无用的信息区域,因此本文构建图像掩模,利用roifill函数在图像中填充指定的感兴趣区域多边形,求解拉普拉斯方程,从多边形边界上的像素值平滑地向内插值,提取线结构光条纹区域,再采用最大类间方差法进行二值化处理。针对条纹二值化图像边缘存在的不连续特征点,采用形态学闭运算操作得到感兴趣的条纹区域(见图6)。

图6 感兴趣区域提取Fig.6 Region of interest extraction.(a) Actual laser stripe image; (b) Processed image

3.1.2 基于PCA的改进Steger法提取光条中心

常见的线激光条纹中心线提取算法有极值法、几何中心法、灰度重心法、Steger法等方法[17]。其中极值法、几何中心法、灰度重心法易受环境噪声及被测物表面粗糙度影响;Steger算法精度较高,但是需要Hession矩阵五次二维卷积,运算量过大,效率低[18]。为提高钢领内表面圆度的测量效率,本文对感兴趣区域进行2次高斯卷积得到其梯度分布,采用主成分分析法确定初始位置的法线方向,沿法线方向进行二阶泰勒展开得到亚像素级中心点。

1)对线结构光的感兴趣区域进行二维高斯卷积计算,其表达式为

(10)

(11)

由于初始位置两侧的像素呈现对称分布,即Gx和Gy的期望值为零,则特征值和特征向量的表达式为

(12)

式中:v1和v2为特征向量;λ1、λ2为特征值。

根据梯度向量的协方差矩阵的物理意义,存在绝对值最大的特征值对应的特征向量为条纹的法线方向。因为λ1>λ2,故λ1对应的特征向量v1为条纹法线方向,对v1进行归一化处理得到条纹法线方向的单位向量n=[nx,ny]T。

3)在确定条纹的法线方向基础上,以条纹梯度绝对值的极小值点(x0,y0)为初始位置,沿着法线方向将初始点的灰度值函数进行二阶泰勒展开得

I(x0+tnx,y0+tny)=I(x0,y0)+

(13)

本文方法与传统Steger算法提取结果如图7所示,传统Steger算法提取所用时间为0.018 4 s,本文方法提取所用时间为0.002 9 s。相较于传统算法,本文算法提取时间大大缩短。

图7 光条中心提取结果Fig.7 Extraction results of light center. (a) Traditional Steger algorithm; (b) Method of this paper

3.2 基于点云数据的圆度测量模型

(14)

式中:i为光条中心数据点数;j为采集到的光条图像数。

由于旋转轴与Y轴平行,则表达式为

(15)

式中,α=j/360。

由式(15)得到钢领内表面的三维点云数据,如图8所示。

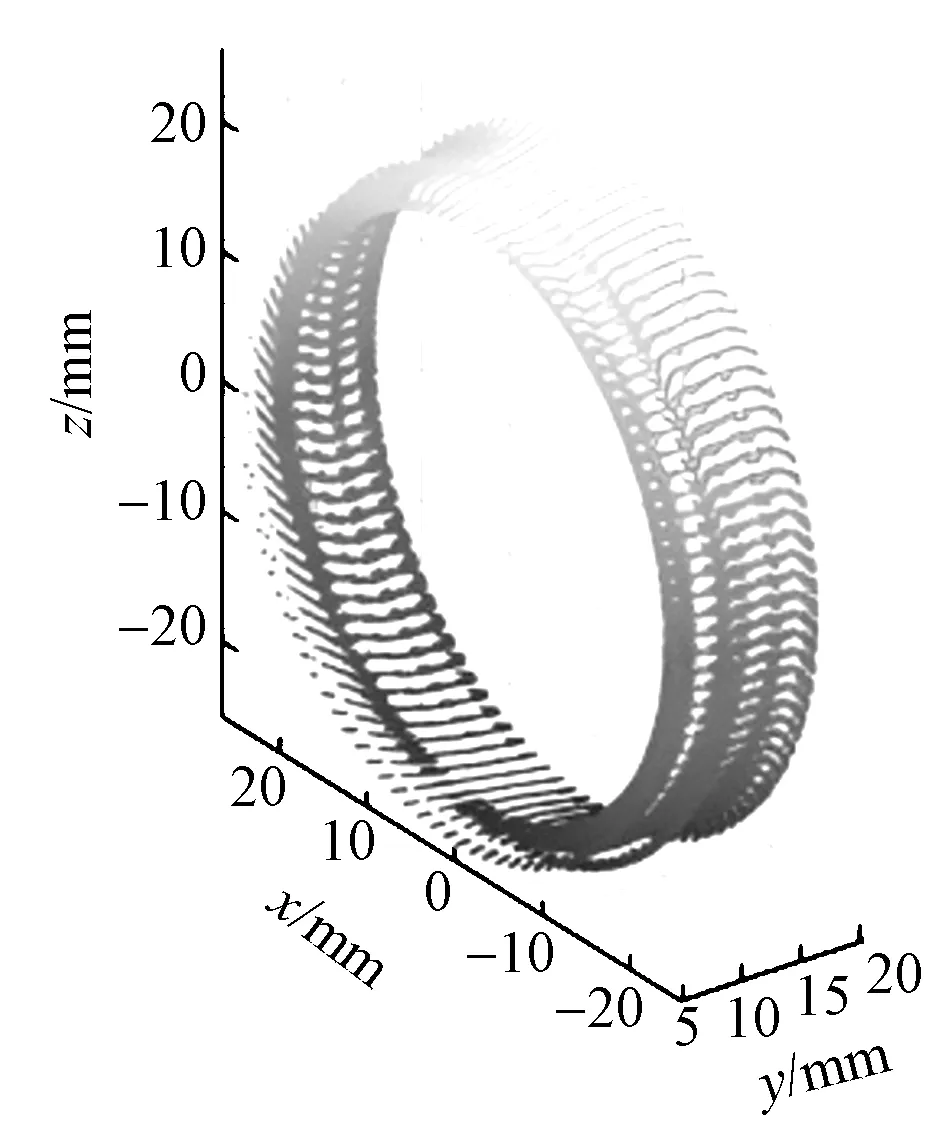
图8 点云数据Fig.8 Point cloud data

建立与旋转轴垂直的虚拟平面,该虚拟平面方程为

(16)

通过点到虚拟平面距离的方式,可得到虚拟平面内的点。

(17)

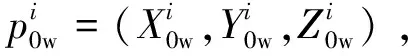
(18)

由式(18)得到圆度误差测量值:

ΔR=Rmax-Rmin

(19)

4 实验数据分析

4.1 实验用钢领

为验证本文方法,选取如图9所示的3种型号钢领。PG1-3854型钢领内径为38 mm,圆度公差为0.1 mm;PG1-4554型钢领内径为45 mm,圆度公差为0.1 mm;PG1-5160型钢领内径为51 mm,圆度公差为0.14 mm。

图9 3种型号的钢领Fig.9 Three types of steel ring

4.2 测量数据分析

3种不同型号的钢领内表面点云数据如图10所示。通过三维点云数据对3种型号钢领建立不同的虚拟平面,代入到式(19)中得到如表1所示的圆度误差,所得3种型号的钢领圆度误差均小于规定的公差值,表明钢领均为合格产品。

表1 不同型号钢领的圆度测量值Tab.1 Measurement value of roundness for three models

图10 钢领内表面点云数据Fig.10 Reconstruction of inner surface of steel ring

将本文方法与文献[3]方法、三维测量仪 (OCG) 法进行对比分析,数据如表1所示。对比数据可知,钢领均为合格钢领,3种方法均可以对钢领内表面圆度误差进行量化表达。本文方法的最大偏差为5.8 μm,文献[3]的最大偏差为7.4 μm,较准确地测出了钢领内表面的圆度误差。

选取PG1-4554钢领进行5组重复性偏差实验,结果如表2所示。可见,本文方法的标准差为0.725,文献[3] 方法的标准差为1.527。本文方法可实现对全部钢领表面轮廓进行测量,算法运行时间小于40 ms。

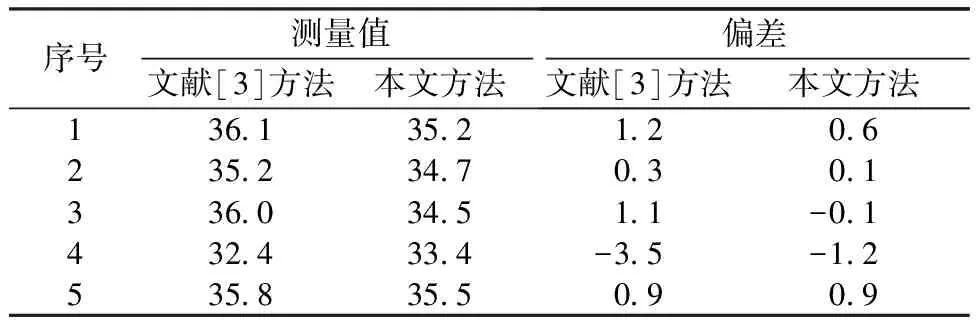
表2 钢领内表面圆度重复性偏差测量值Tab.2 Measurement value of repeatability deviation of inner surface roundness of steel ring μm

5 结 论

1)提出了基于线结构光的钢领内表面圆度测量方法,实现了钢领内表面圆度的非接触式测量,测量精度为 0.006 mm, 算法运行时间小于40 ms,重复性标准差为0.725。

2)提出了基于主成分分析的改进Steger方法,通过2次高斯卷积计算得到线结构光条纹梯度分布,采用主成分分析确定条纹初始位置的法线方向,在该方向上进行二阶泰勒展开,得到钢领内表面条纹的亚像素级中心,大大缩短了传统算法的时间。

3)通过相机标定的内外参数、光平面标定方程及旋转轴标定方程,由线结构光条纹中心得到钢领内表面三维点云数据,结合圆度评价方法建立了基于点云数据的钢领内表面圆度的测量模型。