大尺寸异形结构芯模编织策略及纱线轨迹预测
2023-12-05李麒阳季诚昌郗欣甫孙以泽
李麒阳, 季诚昌, 郗欣甫, 孙以泽
(东华大学 机械工程学院, 上海 201620)
编织技术是织造复合材料预成型体的重要工艺,在汽车制造、医疗器械、航空航天等领域[1]中,编织复合材料已得到广泛应用,但是仍存在大尺寸构件编织误差大、覆盖率不均匀等行业内急需解决的问题。
针对大尺寸异形结构芯模,由于其结构的复杂性,需要使用机器人牵引芯模按照一定轨迹进行编织,轨迹影响到织物的编织角、覆盖率等重要工艺参数,直接影响到复合材料成品的力学性能。Gondran等[2]提出针对复杂芯模编织过程的牵引速度曲线的逆向求解方法,并使用工业机器人辅助完成编织;Chi等[3]建立了单机器人牵引复杂芯模进行编织的近似求解方法,提高实际生产效率;Martinec等[4]针对纤维缠绕过程中的牵引机器人的工作过程进行分析,计算得到机器人的轨迹。但是以上研究内容应用于大尺寸芯模的编织具有局限性,由于芯模的尺寸较大,单机器人夹持芯模进行编织由于重力等因素会造成较大的编织误差,所以大尺寸的异形结构芯模难以实现精确编织。为解决该问题,Meng等[5]建立了机器人牵引过程的位置补偿模型,对机器人末端进行位置补偿,尽量减少纱线作用力及重力等因素带来的编织误差。
编织过程中更改牵引速度与主机速度或者更换导向环尺寸会形成不同性能的复合材料预成型体,故需要纱线轨迹预测模型来预测不同编织情况下的编织角,在实际生产中可提高生产效率。研究人员建立了一系列编织过程的纱线模型:Du等[6]针对变截面复杂芯模编织过程进行分析,建立主机速度与牵引速度的关系,调整纱线轨迹预测编织角;Swery等[7]提出使用有限元法模拟编织过程,并取得较好的效果;Monnot等[8]建立编织模型适用于非轴对称几何形状和弯曲中心线的芯模,使用纱线沉积模型计算落点位置。
在实际生产过程中,对于大尺寸复杂结构芯模的编织一般使用双滑台牵引芯模,可保证芯模在编织过程中不易折断或掉落,但是编织异形结构芯模时,传统方式难以保证中心线时刻垂直编织平面,造成较大的编织误差。使用单一机器人进行编织时由于芯模重心与夹持点距离较长,会导致机器人负载不足或产生纱线落点偏差等现象,故本文针对双机器人协同编织过程进行分析,对其同时夹持芯模穿过落点平面的轨迹进行计算求解,保证双机器人夹持芯模时工具坐标系相对静止,同时提出针对机器人牵引芯模编织的纱线轨迹预测模型,考虑机器人运动轨迹、复杂芯模的几何特征以及收敛长度的变化等因素,进而对纱线落点的位置进行计算。本文提出轨迹求解算法拟提高轴线为任意空间曲线的异形芯模的编织精度,并相对准确地预测截面为圆形的芯模上纱线的落点轨迹,对实际生产起到指导作用。
1 牵引机器人轨迹计算
1.1 机器人牵引系统
双机器人牵引装置如图1所示,2台机器人分别用R1和R2表示,在双机器人的运动过程中,需分别考虑到2台机器人的工具坐标系与基坐标系。工具坐标系原点设定在法兰上的三爪卡盘中心,用xTool,yTool,zTool表示,其中垂直法兰面向外为zTool轴正方向,芯模中心线以及形状信息在工具坐标系下进行描述;基坐标系设定在机器人底座,用来描述2台机器人的相对位置关系以及机器人和编织机的位置关系,用x,y,z表示。

图1 编织机与双机器人牵引系统Fig.1 Braiding machine and dual-robot take-up system
1.2 双机协同轨迹求解
在编织过程中,不同运动方向的纱线交织在一起穿过导向环后覆盖在芯模表面,为得到相对均匀的织物,机器人夹持芯模需保证芯模始终垂直通过编织平面(见图2),编织平面与导向环平面平行且直线距离为初始收敛距离,设定初始收敛距离为h0。为方便求解任意形状芯模的牵引轨迹,对芯模进行离散化处理,沿芯模中心线C将其分解成间距为d的n个离散点C(i) (i=0,1,…,n-1)来表示,相邻2点组成一段离散芯模,且将任意一段离散芯模半径的变化近似为线性函数:
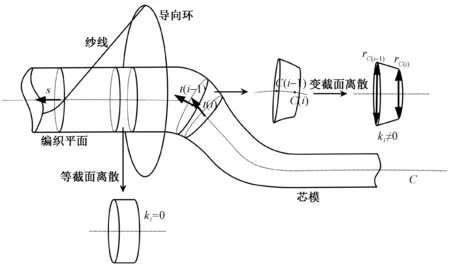
图2 编织过程示意图Fig.2 Schematic diagram of braiding process
rC(i)=rC(i-1)+ki·xc
(1)
式中:rC(i-1)和rC(i)分别为在C(i-1)与C(i)点处芯模截面的半径;ki为该段芯模的半径变化系数;xc为芯模点C(i-1)与C(i)间的长度变量。同时,离散点数目n有足够的精度定义芯模形状。
针对双机器人共同夹持1根芯模进行编织的过程,需要分别对2台机器人在各自基坐标系下的工具中心点(TCP)数据进行求解,工具中心点TCP包括x、y、z、a、b、c6个值。其中:x、y、z表示工具坐标系原点在基坐标系中的位置信息;a、b、c表示工具坐标系绕z轴、y轴和x轴旋转的角度。本文针对每段离散芯模的几何特征进行机器人轨迹求解,流程图如图3所示。

图3 机器人轨迹计算流程图Fig.3 Flow chart of robot trajectory calculation
本算法需要起始编织时芯模端面达到编织点平面的TCP数据、初始收敛长度h0、编织机位置条件、双机器人的位置关系以及芯模几何条件作为初始条件进行迭代求解。首先求解机器人R1在第i段芯模起始位置旋转平移到终点位置的变换矩阵,保证C(i)点处切向量t(i)与编织平面法向量s方向一致,且C(i)与编织平面中点S的位置信息在基坐标下重合,使用RPY(Roll, Pitch, Yaw)法进行TCPR1(i) 数据的求解;再通过R1与R2的位置关系、TCPR1(i)的数据以及工具坐标系相对静止的约束条件求解出机器人R2在该段编织过程的变换矩阵,进而求解TCPR2(i)的数据。
对第i段进行编织时,通过式(2)对C(i)点处切向量t(i)进行坐标变换,使用齐次坐标变换将工具坐标系下的向量t(i)转换为基坐标系下的向量tb(i)。
(2)
式中:aR1(i-1)、bR1(i-1)、cR1(i-1)分别表示上TCPR1(i-1)中的姿态数据;Rot表示旋转变换,Rot(z,aR1(i-1))为绕z轴逆时针旋转角度aR1(i-1),Rot(y,bR1(i-1))为绕y轴逆时针旋转角度bR1(i-1),Rot(x,cR1(i-1))为绕x轴逆时针旋转角度cR1(i-1)。为使tb(i)与编织平面法向量s方向一致,机器人需要夹持芯模旋转角度φ,故旋转矩阵为
Roti=Rot(f,φ)·Roti-1
(3)
(4)

(5)
(6)
式中:xs,ys,zs为编织平面中点S在R1基坐标系下的位置信息;xCb(i)、yCb(i)、zCb(i)分别表示该姿态下C(i) 与R1工具坐标系原点组成的向量在R1基坐标系下各轴的投影长度。位置信息xR1(i),yR1(i),zR1(i) 可从变换矩阵直接读出,同时,使用滚、仰、翻变换解求解工具坐标系姿态角度,如下式所示:
针对第i段芯模编织过程中R2机器人末端的位置与姿态TCPR2(i),其位置信息在2个机器人工具坐标系相对静止的约束条件下通过式(8)得出:
(8)

2 纱线轨迹预测模型
2.1 模型假设
对于大尺寸异形结构芯模的编织过程,本文提出模型基于以下假设:1) 忽略纱线间以及纱线与编织环间的摩擦力与相互作用力;2) 忽略纱线厚度;3) 忽略编织过程中携纱器在底盘蜿蜒运动;4) 忽略编织过程中纱线张力波动。
2.2 数学模型
在编织过程中,编织机自身携带多组锭子按照规定好的转速沿底盘的蜿蜒轨道做顺时针和逆时针的近似圆周运动,机器人夹持芯模按照设计好的轨迹与速度持续推进,通过配合,纱线从锭子出发穿过导向环,最后覆盖在芯模表面形成复合材料预成型体。恒截面直线型芯模编织是静态稳定的,易对纱线的轨迹进行预测,预成型体的编织角可通过编织过程中的几何关系计算得到,具体数学关系如下:
(9)
式中:θ为编织角,是单根纱线与芯模中心线所形成的夹角;Rg为导向环半径;r为芯模半径;H为收敛距离。稳定编织过程中,编织角还可通过牵引速度与主机速度进行计算[9],其关系如下:
(10)
式中:ω为编织机主机速度,即锭子运动的角速度;V为牵引装置夹持芯模运动的速度。
在实际应用中,大部分复杂构件芯模的弯曲程度及截面半径是任意且变化的,故存在动态不稳定编织阶段[10],在该阶段弯曲或者变截面芯模使编织过程的收敛距离不断变化[11],导致编织角难以预测(见式(9))。
编织过程中芯模纱线及导向环的位置关系如图4所示。本文设定芯模端面坐标系{xm,ym,zm}为固定坐标系,由于实际编织过程中机器人夹持芯模穿过编织机的过程较为复杂,为提高预测效率,本文根据相对运动关系,将编织机简化为由导向环与锭子轨道组成的2个圆环,同时将实际编织过程转换为圆环穿过芯模的过程,大幅度节省计算时间,因此,编织机上锭子q的运动轨迹为复杂的空间螺旋线,其中心线Q由机器人轨迹决定,根据机器人轨迹中牵引速度V得到每个离散点对应的时刻T,进而得到螺旋线的数学表达式如下:

图4 芯模、纱线与导向环的几何关系Fig.4 Geometric relationship between mandrel, yarn and guide ring
(11)
式中:Qj为中线上离散点;qi,j为第i个载体在Tj时刻下的空间位置;tj为Qj对应的单位切向量;rsp为线轴出口平面的半径;θi,j为Tj时刻下第i个载体编织机上的角度位置。
在环形编织机工作过程中,每根纱线按照类似的运动轨迹变化规律交织在芯模上形成织物,且纱线间作用力被忽略,纱线从出纱口出发,经过导向环时纱线弯折后形成收敛区域,最终落在芯模表面,故根据几何关系求解得到纱线与导向环的交点g,进而判断纱线是否落在芯模表面。
对芯模数据进行处理,读取STL格式下的三维模型,得到芯模表面在芯模端面坐标系下的空间位置信息,根据每条纱线与导向环的交点g、已知落点p及落点所在三角面片上指向芯模外侧的法向量nM的几何位置确定是否已经落在芯模表面,判断条件如下:
nM·(gi,j-pi,j)≤0
(12)
当判断纱线已落在芯模上表面,定义此刻的三角面片为F,纱线在三角面片F上的轨迹方向为向量(gi,j-pi,j)在三角面片F上投影的方向,长度为已知落点p到三角面片边界的长度,根据以上约束条件对落点p位置进行更新,计算公式如下:
(13)
(14)
式中:(gi,j-pi,j)F为纱线在三角面片F上的投影;MF与M′F分别为三角面片F上纱线指向的边缘所对应的2个顶点坐标;nd为三角面片F上纱线所指向的边缘线与F的法向量nF所形成平面的法向量。
根据环形编织过程的连续性,同时针对所有纱线进行轨迹预测,对每个步长进行纱线位置判断,准确计算纱线在芯模表面的分布及编织角的大小等,预测过程如图5所示。可根据任意机器人轨迹及任意形状芯模进行计算,计算速度快。

图5 纱线轨迹预测过程Fig.5 Yarn trajectory prediction process
3 实验验证
本文提出计算双机器人协同编织复杂芯模的轨迹计算方法以及机器人牵引编织过程的纱线轨迹预测方法,为验证机器人轨迹精度与预测模型的准确性,以轨道交通行业某大尺寸异形结构件为例进行编织实验,对本文纱线轨迹预测模型的结果与实际编织织物进行对比,分析模型适用性,同时对预成型体编织角进行测量,比较测量值与期望值偏差。
计算过程使用MatLab R2020b软件进行分析,在配备AMD R7-4800H的CPU、GeForce RTXTM 2060的GPU,16 GB的RAM与Windows10操作系统的电脑上进行。
实验设备为1台大型环形编织机、2台六自由度工业机器人。其中环形编织机包括240个锭子,每个锭子上携带有1个纱筒进行编织,编织机的运动系统包括4个伺服电动机、2个振动电动机以及其控制器。机器人为KUKA六自由度工业机器人KR 250 R2700-2。
通过计算得到的机器人轨迹保证芯模垂直通过编织平面,尤其在弯曲部分,远离编织平面的机器人末端执行器运动行程较大,图6示出双机器人夹持芯模编织过程的TCP点坐标值。
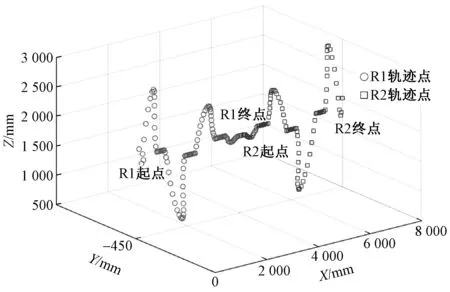
图6 编织过程双机器人TCP变化过程Fig.6 TCP change process of dual-robot in braiding process
从图6可以看出,双机器人末端执行器运动轨迹通过芯模的几何形状进行约束,同时运动到任意点时末端执行器保证相对静止。
对编织后的预成型体进行测量,在非弯曲处使用游标角度尺测量单根纱线与轴线之间的角度以获得编织角,在弯曲处难以使用游标角度尺,故使用电子数显角度尺测量2根交织纱线之间的夹角再取一半获得编织角。然而,弯曲处织物的编织角由于芯模几何原因导致在圆周方向不相等,本文根据该复合材料结构件的力学要求,对编织角要求较高的面进行测量记录。通过预测模型模拟出的织物结构与实际织物结构如图7所示。可以看出:芯模在截面不发生变化时,编织角相对稳定;当截面面积发生变化时,编织角也发生一定变化。同时对织物编织角的测量值与预测值进行对比,如图8所示。可以看出,在横截面非弯曲位置编织较为稳定,测量值与预测值之间的误差以及测量值与期望值之间的误差均较小,在±3°以内。在弯曲变截面处,芯模的复杂性使得编织处于非稳定编织阶段,由于纱线间相互作用力等因素的影响,测量值与预测值之间的误差在±5°以内,测量值与期望值之间的误差在±7°以内。

图7 真实纱线结构与预测结构对比Fig.7 Comparison between real(a)and predicted(b) yarn structure
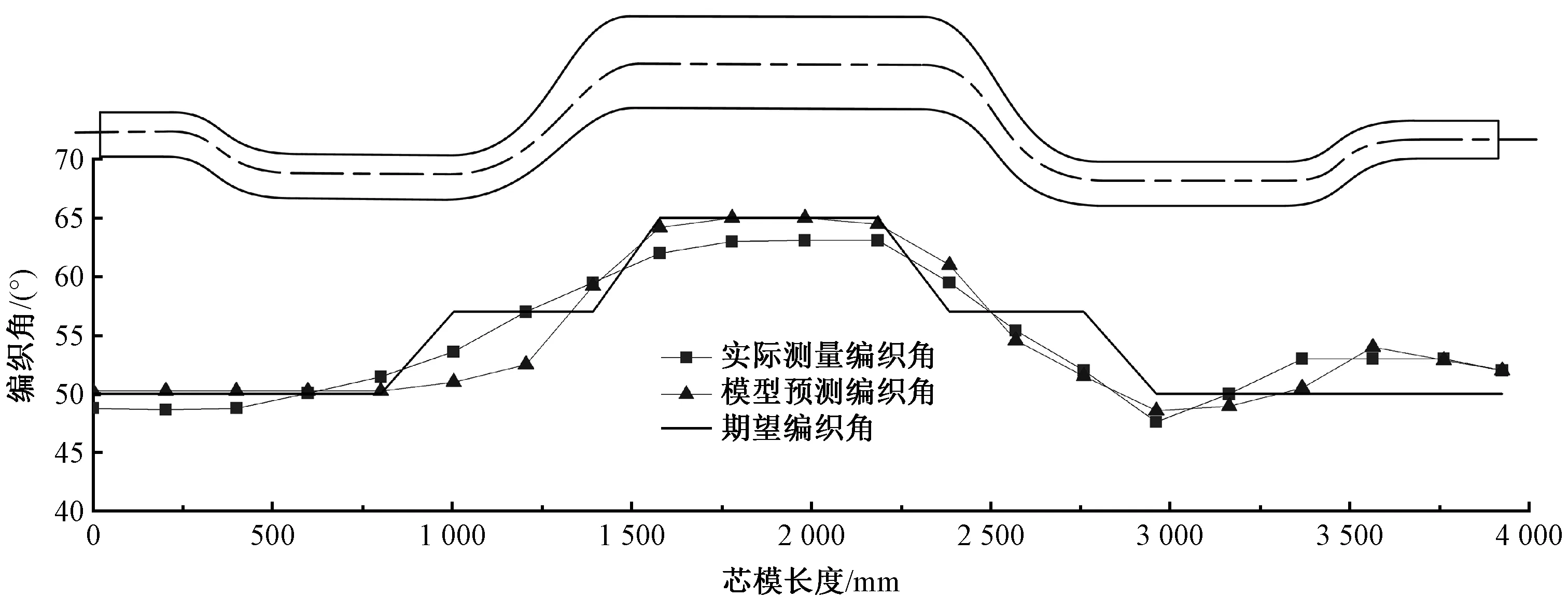
图8 不同位置织物期望值、实际值与预测值对比Fig.8 Comparison of expected value, actual value and predicted value of fabrics at different positions
4 结 论
本文提出针对大尺寸异形结构芯模的编织方法,对双机器人同时夹持芯模的编织过程进行数学分析,在保证芯模时刻垂直通过编织平面的基础上,求解双机器人的运行轨迹;同时,提出一种纱线轨迹预测方法,针对双机器人运动过程的牵引轨迹,精确预测纱线落点变化。通过分析编织得到织物的编织角发现,使用本文方法求解的轨迹进行编织可以使织物的编织角与期望值的等截面部分误差保证在±3° 以内,弯曲变截面部分误差保证在±7°以内。同时,预测结果与实际结果等截面部分误差保证在±3° 以内,弯曲变截面部分误差保证在±5°以内。本文提出的双机器人轨迹求解方法可解决大尺寸异形结构芯模的编织问题,同时纱线轨迹预测模型可对异形结构芯模进行精确预测,提高编织效率,在相同条件下提升了复合材料的力学性能。
