基于临界水力梯度接近度的工程管涌危险程度量化研究
2023-12-04钱叶琳张振华李长春王磊磊
钱叶琳, 苏 颖, 张振华, 李长春, 王磊磊, 徐 阳
(1.安徽省路港工程有限责任公司,安徽 合肥 230031; 2.合肥工业大学 土木与水利工程学院,安徽 合肥 230009)
水利工程在建设或者运行期间时常发生管涌。1998年长江全流域发生特大洪水,中下游堤防险情73 800余处,长江流域干堤发生较大管涌872处,占较大险情的51.2%,直接经济损失达1 500亿元[1]。2016年全国大范围地区出现的持续强降雨汛情中,湖北、湖南、江西、安徽、四川等多地共发现并治理了608处堤坝管涌决口,并对长达37.5万余米的堤防大坝进行了加固[2]。某基坑在开挖过程中坑内涌水涌砂2 800 m3,地面塌陷500 m2,深6~8 m,抢险历时6 d,动用抢险人员累计2 000余人次,不仅影响施工工期,而且严重影响到附近高层建筑的安全,造成了巨大的经济损失[3]。
目前对于管涌的研究主要集中在土体发生管涌的临界条件以及工程中管涌发生危险性的研究上[4-5]。文献[6]以单个土颗粒为研究对象,按照渗透力与土颗粒浮重间的极限平衡推导出砂砾土临界水力梯度计算公式;文献[7]考虑多孔介质中的流动,并与伯努利方程和临界牵引应力条件耦合,建立了计算临界水力梯度的模型;文献[8]采用泥沙颗粒滚动理论,同时考虑土壤颗粒的相对暴露程度和渗流方向建立二维渗流模型,预测了土壤颗粒运动的临界水力梯度;文献[9]利用多个方程构建层流管道模型,得出反向侵蚀导致堤坝破坏的临界水力梯度公式;文献[10]根据相对运动原理,推导出考虑周围粒子受水流拖拽力影响的无黏性土临界水力梯度;文献[11]将蒙特卡罗法与有限差分法相结合进行程序开发,用于预测蓄水后土石坝发生管涌的可能性,并通过案例对程序进行验证;文献[12]考虑水力参数的不确定性,开发了一种基于简单脆弱性指数的程序,并通过工程实例论证了该程序的可行性;文献[13]基于微震链阵列调查结果可揭示滑坡与堤坝的内部结构以及自电位调查结果可显示异常渗流带的路径,采用微震链阵列与自电位测量方法来预测滑坡以及大坝发生管涌的可能性;文献[14]通过研究管涌发展过程中声发射特征,得出声发射信号的活动与管涌不同阶段有关的结论,据此将声发射信号作为监测管涌发展的指标来判断管涌发生的危险程度。
然而在工程上临界水力梯度通常用于判定出险部位是否发生了管涌,但不能对管涌区以外区域进行管涌危险性识别;现有的管涌危险性预测方法不能达到定量预测的效果,在工程中应用具有一定的局限性。因此有必要提出一种可以定量判别工程中发生管涌危险程度的方法,以此为防渗加固措施的实施提供科学依据。本文基于土体发生管涌的水力条件[2]提出临界水力梯度接近度指标,该指标可以定量判别土体发生管涌的危险程度,从而得出管涌危险区分布,并结合工程实例对该指标进行合理性论证。
1 工程概况
某船闸基坑东西长457.0 m,南北宽112.0 m,基坑上闸首底部设计开挖高程为17.0 m,临近河道水位高32.5 m。基坑在开挖之前沿四周实施一道高压摆喷墙形成防渗体系。基坑在开挖至高程24.2 m、17.0 m时出现了2次涌水事故。基坑现场及涌水路线如图1所示。
根据钻探资料和实测资料,将该船闸地层划分为5层含水层和2层隔水层:第1含水层为潜水,分布在①层素填土、②层壤土中(标高32.5 m);第2含水层为承压水,分布在③层砂壤土夹粉质壤土中(标高23.0~29.0 m);第3含水层为承压水,分布在④层砂壤土中(标高15.0~20.0 m);第4含水层为承压水,分布在⑤层轻粉质壤土夹砂壤土、⑥层砂壤土中(标高2.0~10.0 m);第5含水层为承压水,分布在⑦层粉砂、⑧层砂壤土中(标高-11.0~<2.0 m);第1隔水层为③-1层壤土;第2隔水层为④-1层壤土。某船闸基坑地层及含水层分布如图2所示。

图2 某船闸基坑地层及含水层分布
2 临界水力梯度接近度

(1)
其中:i为土体的水力梯度;ic为土体临界水力梯度。
3 数值模拟
3.1 基本理论
3.1.1 渗流控制方程
饱和-非饱和渗流理论假定水在非饱和土中仍然服从Darcy定律,然后根据水流的连续性条件以及孔隙水压力不随时间变化的假定,在不考虑不同流体的流动与土体结构平衡条件之间相互作用的条件下(即不考虑孔隙水与孔隙水的流动对土体结构变形的影响),通过土体非饱和区域内的地下水控制方程式[16]为:
(2)
本文渗流计算是在土体饱和状态下进行的,此时地下水的控制方程式为:
(3)
其中:kx、ky分别为土体x、y方向的渗透系数;H为位置水头与孔隙水压力两者之和;Q为微元体的边界流量;mw为体积含水量变化系数;γw为水的容重。
3.1.2 定解条件
初始条件为:
(4)
边界条件为:
(5)
其中:H0(x,y,t)为点(x,y)处初始水位;Γ1为一类边界条件;H1(x,y,t)为点(x,y)在t时刻的边界已知水位。
3.2 数值计算模型及边界条件
基坑涌水位置发生在上闸首处,因此取该区域为研究对象,根据图纸以及现场情况确定该基坑研究范围长为120.0 m,宽为42.0 m,深度为17.0~34.5 m。为减小边界范围选取过小给计算结果带来误差,选取研究对象最大几何尺寸的3~5倍确定计算范围,最终确定整体模型尺寸为900.0 m×540.0 m×134.5 m,网格类型为4节点SOILD181以及8节点SOILD185,如图3所示。

图3 基坑整体数值计算模型
数值模型的渗流边界条件为:顶面、底面为不透水边界;前、后、左、右边界为透水边界(水位32.5 m);防渗结构均不透水。沿基坑轴线方向剖面边界条件如图4所示。基坑最初防渗体系数值模型如图5所示。

图5 基坑最初防渗体系数值模型
3.3 计算参数
在FLAC3D软件中对计算模型进行渗流计算[17],以每个网格为研究对象,根据上文提出的临界水力梯度接近度计算公式,利用FISH语言进行二次开发,计算获得基坑涌水剖面的水力梯度以及临界水力梯度接近度分布。计算时将土层赋予摩尔库伦模型[18-19],防渗结构赋予线弹性模型[20-21],同时将防渗结构赋予各向同性不透水模型[22]。根据计算时的参数需求,在该船闸基坑处取样进行三轴试验并结合参考现场《地质勘查报告》,确定计算参数,其中各地层的临界水力梯度计算公式参考文献[6]。
计算参数见表1所列。
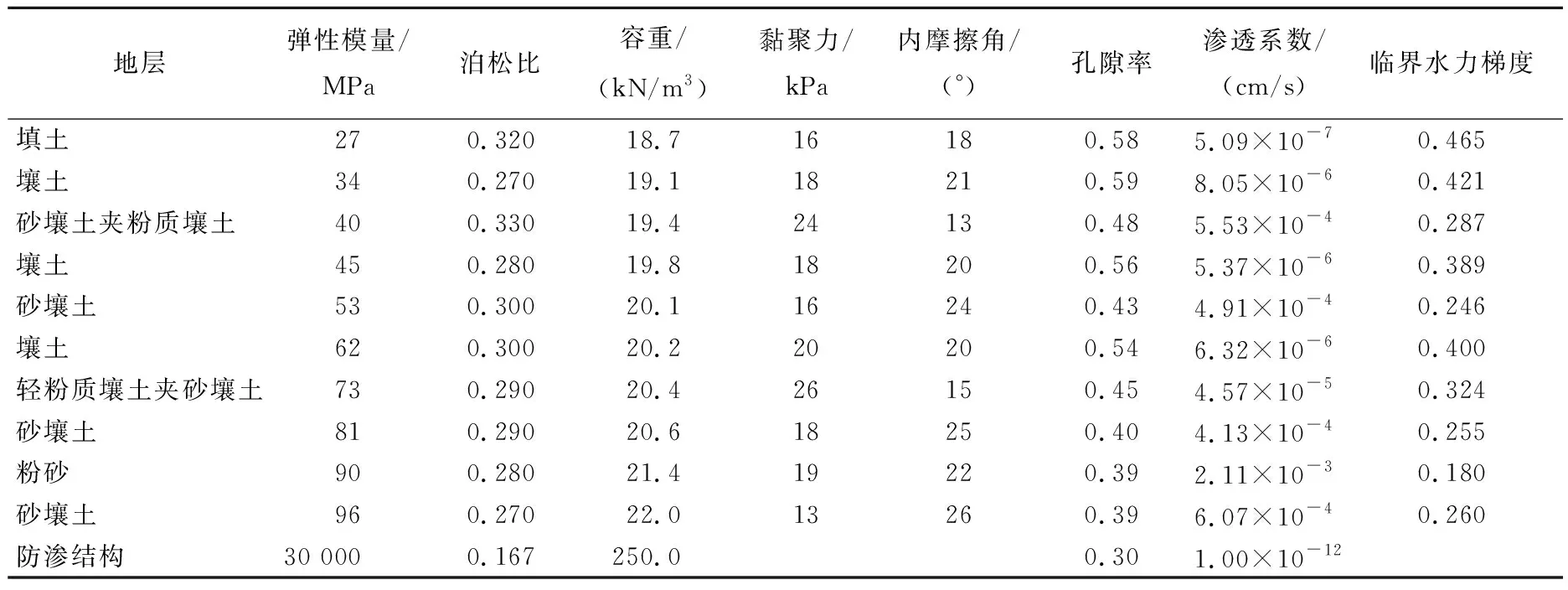
表1 各土层计算参数
3.4 计算步骤
为分析该基坑施工过程中水力梯度以及临界水力梯度接近度分布随管涌产生与基坑防渗加固的演化规律,本文确定了以下4个计算步骤:
1) 基坑开挖至坑底高程为24.2 m,发生第1次涌水。
2) 针对基坑第1次涌水事故进行防渗加固。
3) 基坑开挖至坑底高程为17.0 m,发生第2次涌水。
4) 针对基坑第2次涌水事故进行防渗加固。
4 数值模拟结果及分析
4.1 第1次涌水剖面计算结果
基坑第1次涌水剖面水力梯度与临界水力梯度接近度计算结果如图6所示,此时坑底土层为砂壤土夹粉质壤土。

图6 基坑第1次涌水剖面水力梯度与临界水力梯度接近度计算结果
从图6a可以看出,此时坑底涌水剖面出水口处的水力梯度为0.460,大于该土层临界水力梯度0.287,说明此处发生了管涌;从图6b可以看出,涌水剖面的管涌危险区主要分布在防渗结构与其周围土体以及防渗结构底部绕渗区。
根据计算结果,涌水部位的临界水力梯度接近度大于1,基坑发生管涌的原因是在防渗结构处出现了绕渗,形成了渗流破坏贯通区,造成在基坑底部发生管涌。通过以上对比得出,临界水力梯度用于判定浅表层涌水位置土体是否发生了管涌,对于涌水部位以外的土体无法进行管涌危险性判定;而临界水力梯度接近度可以依据土体发生管涌的危险程度划分出管涌危险区,可以判定整个场地内土体发生管涌的危险性。
根据基坑第1次涌水时管涌危险区分布,需要对管涌危险区进行防渗干预。结合工程现场,在涌水处原高压摆喷墙外侧新增高压摆喷墙,如图7所示。

图7 基坑第1次防渗加固
基坑第1次涌水剖面在防渗加固后水力梯度与临界水力梯度接近度分布的计算结果如图8所示。由图8可知,坑底涌水部位的水力梯度自涌水时的0.460降至0.180,低于该土层的临界水力梯度0.287,此处不再发生管涌;坑底涌水口的临界水力梯度接近度较加固前降低至小于1,渗透破坏贯通区域远离坑底,说明针对本次涌水时管涌危险区分布而提出的防渗加固建议有效。

图8 基坑第1次涌水防渗加固后涌水剖面水力梯度与临界水力梯度接近度计算结果
4.2 第2次涌水剖面计算结果
基坑第2次涌水剖面水力梯度与临界水力梯度接近度计算结果如图9所示,此时基坑已开挖至设计高程,坑底土层为砂壤土。

图9 基坑第2次涌水剖面水力梯度与临界水力梯度接近度计算结果
从图9a可以看出,此时坑底涌水剖面出水口处的水力梯度为0.540,大于该土层临界水力梯度0.246,说明此处发生了管涌;从图9b可以看出,此时涌水部位的临界水力梯度接近度大于1,基坑发生管涌的原因是在防渗结构处出现了绕渗,形成了渗流破坏贯通区,最终造成在基坑底部发生管涌。经过对比得出临界水力梯度无法对涌水部位以外区域的土体进行管涌危险性判定,而临界水力梯度接近度可以依据土体发生管涌的危险程度划分出管涌危险区,可以判定整个场地内土体发生管涌的危险性。
根据基坑第2次涌水时土体管涌危险区分布,需要对管涌危险区进行防渗干预。结合工程现场,在原高压摆喷墙外侧新增混凝土截渗墙,针对出水部位利用钢筋混凝土截渗墙进行防渗补强,如图10所示。基坑第2次涌水剖面在防渗加固后水力梯度与临界水力梯度接近度分布计算的结果如图11所示。
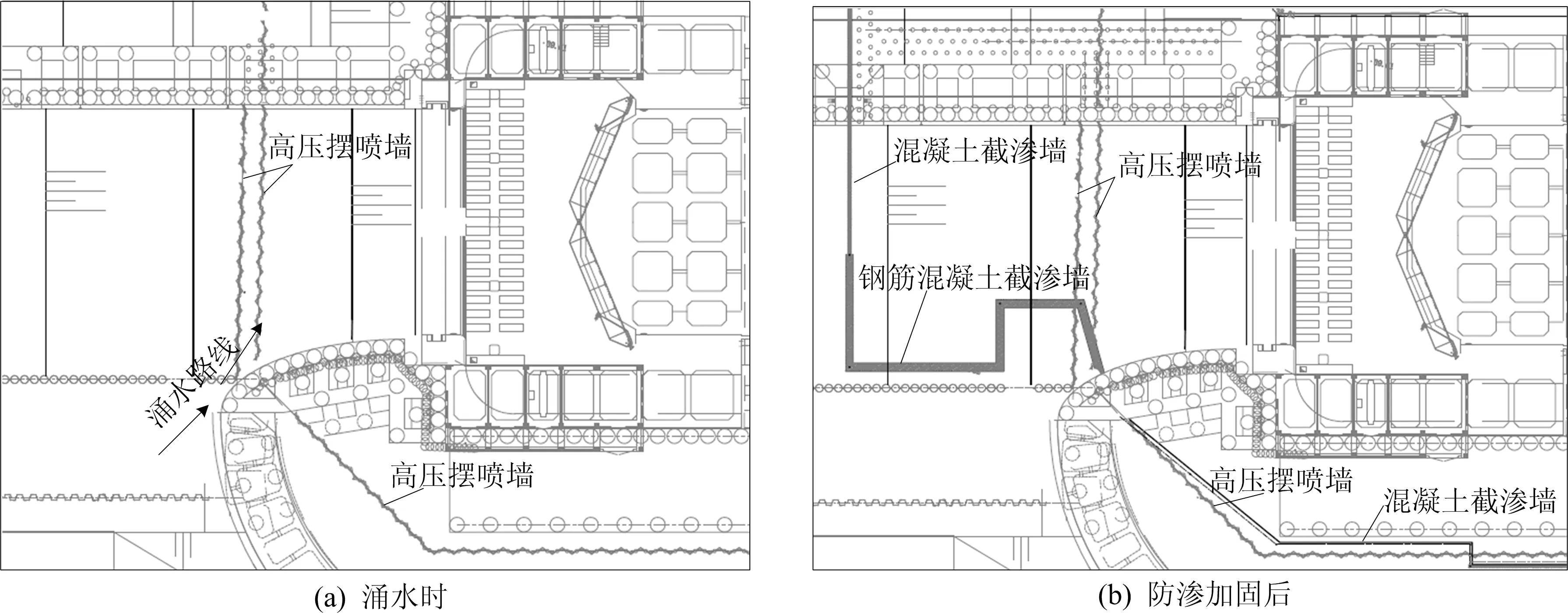
图10 基坑第2次防渗加固
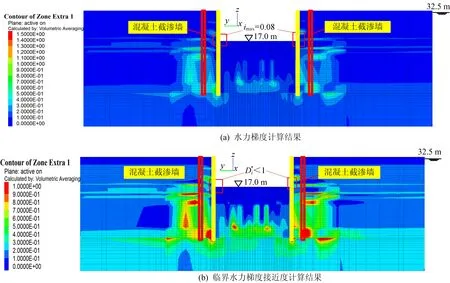
图11 基坑第2次涌水防渗加固后涌水剖面水力梯度与临界水力梯度接近度计算结果
从图11a可以看出,此时坑底涌水部位的水力梯度自涌水时的0.540降至0.080,低于该土层的临界水力梯度0.246,此处不再发生管涌;从图11b可以看出,此时坑底涌水口的临界水力梯度接近度较加固前降低至小于1,渗透破坏贯通区域远离坑底,说明针对基坑本次涌水时管涌危险区分布而提出的防渗加固建议有效。
4.3 讨论
以往工程中对于管涌区的判定只针对浅表层出险区域,如图12所示,但伴随管涌区的出现,管涌潜在危险区也会存在,这些潜在危险区在外界条件或工程结构失稳的进一步影响下就会发展为管涌区,因此能够有效识别管涌潜在危险区同等重要。
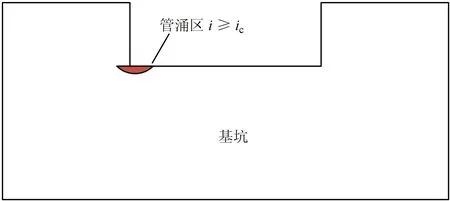
图12 以往管涌研究区域
以往方法因为不能定量预测管涌危险性,所以不能对管涌潜在危险区进行准确识别。文献[6,23-25]通过室内渗透试验依据土样发生管涌的危险程度不同,将土体发生管涌的动态过程定量划分为若干个区间。
本文统计了上述文献得出的不同土体临界水力梯度及其发生管涌潜在危险时(细颗粒普遍流失)的水力梯度,换算得出土体处于管涌潜在危险时的临界水力梯度接近度经验取值,如图13所示。由图13可知,不同土体处于管涌潜在危险时临界水力梯度接近度整体位于0.6~0.8之间,考虑到实际工程安全性,选取临界水力梯度接近度为0.6作为土体处于管涌潜在危险时的判断依据。

图13 相关文献土样临界水力梯度接近度转化结果
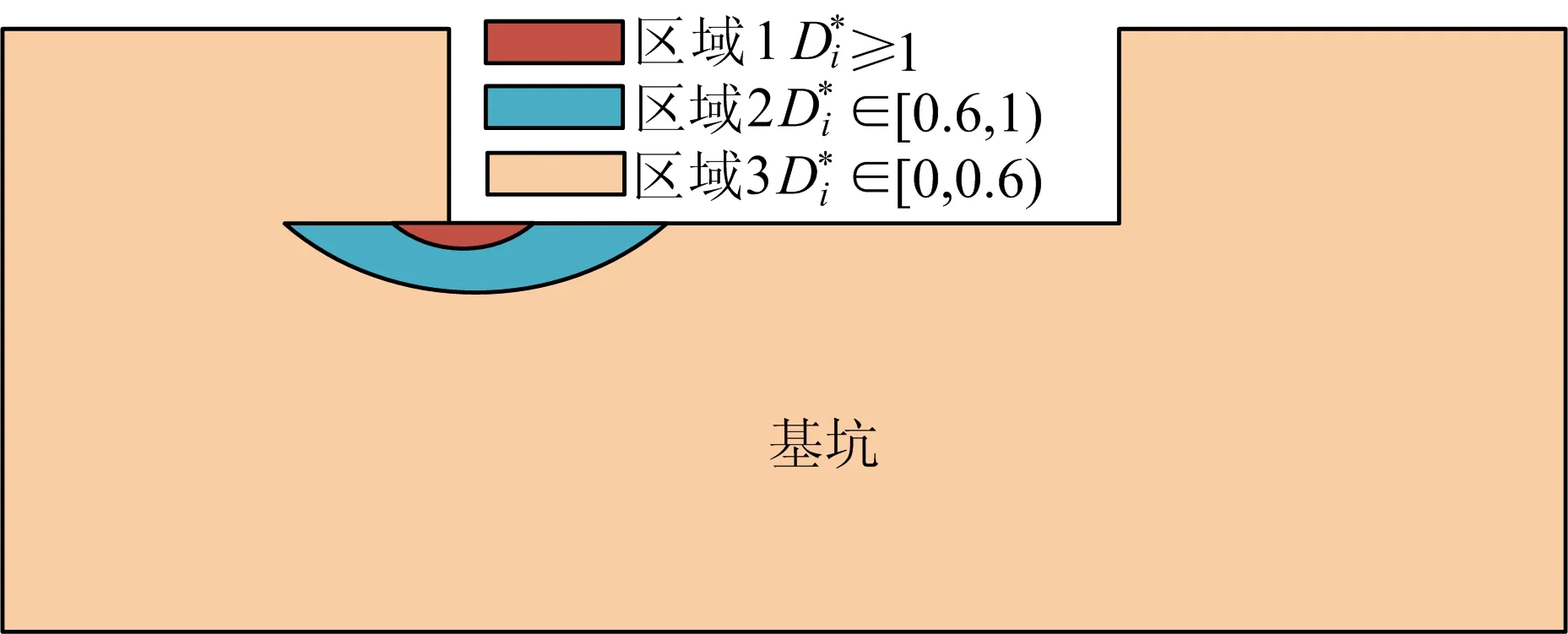
图14 本文临界水力梯度接近度管涌研究区域
通过以上分析得出,临界水力梯度接近度可以根据土体发生管涌的危险程度定量划分区域,通过及时识别管涌危险区以及潜在危险区的分布并提供防治建议,可以有效避免工程发生管涌,具有重要的工程意义。
5 结 论
本文基于土体发生管涌的水力条件,提出可以定量判别工程发生管涌危险性并提供防渗建议的临界水力梯度接近度指标,根据工程实例采用数值模拟方法对该指标进行合理性论证,得出以下结论:
1) 临界水力梯度接近度指标通过表示土体水力梯度与其临界水力梯度的接近程度来定量判定土体发生管涌的危险程度,不仅可以用来判定浅表层涌水位置土体是否发生了管涌,还可以识别复杂土层场地内土体发生管涌的危险性。
2) 根据临界水力梯度接近度分布的计算结果,得出发生管涌的危险区以及潜在危险区,据此分析工程涌水机制,并提供合理的防渗建议,通过提前的防渗干预达到消除管涌的目的。
通过以上研究表明,临界水力梯度接近度指标的提出为土木工程中管涌的预测以及防治提供一种新的管涌危险性评价的量化方法。
