互联电网安全稳定控制系统可靠性评估

2023-12-04李生虎颜云松任建锋

合肥工业大学学报（自然科学版） 2023年11期

李生虎, 张楠, 颜云松, 韩伟, 任建锋, 宋闯

(1.合肥工业大学电气与自动化工程学院,安徽合肥 230009; 2.南瑞集团有限公司(国网电力科学研究院有限公司),江苏南京 211106; 3.国网河南省电力公司电力科学研究院,河南郑州 450052)

电网互联是提高能源使用效率的重要方法,也是当前电网发展的主要趋势。以华东电网为例,当发生直流闭锁时,西北、西南和华中等电网进行跨区功率支援,可能发生频率失稳的问题。同时由于高压直流、柔性交流、风电、光伏等增加,电网稳定控制需求增加,直流闭锁引发有功失衡和频率失稳问题尤为突出[1-3]。安全稳定控制系统(security and stability control system,SSCS)由广域范围内设备故障事件触发,其动作早于低频减载,有助于维持电网频率和功角稳定[4-5]。在SSCS上游设备故障导致下游设备不可用时,电网频率安全受到严重威胁,有必要加强对其可靠性研究。

现有可靠性评估算法均可用于SSCS可靠性评估,如蒙特卡洛抽样[6-9]、故障树分析[10-12]、状态空间法[13-15]等。文献[6]采用基本可靠性分析方法计算SSCS装置的可靠性;文献[10]以装置底层模件为基本单位评估SSCS结构失效概率,而未涉及功能可靠性研究。当站点/通道较多、存在备用站点时,上述方法建模存在难度。

图论方法在网络重构[16]、电网规划、故障诊断[17]等领域已有应用。文献[18]基于有向图连通性,分析设备或网络可靠性;文献[19]判断源荷间连通性,计算变电站风险指标,其中可达矩阵由邻接矩阵进行布尔运算得到;文献[20]给出电气接线任意节点间连通路径算法,其接线相对SSCS结构简单。SSCS加权图具有概率属性,布尔运算不适用[21]。

上述研究均针对SSCS结构失效风险,而SSCS控制目的是在电网突然产生大量功率缺额后,快速提升功率、维持有功平衡。考虑站点控制备用和控制路径的多样性,即使有部分站点或通道故障,也未必一定导致功率缺额。因此需从SSCS设计目的考虑,研究电网发生功率缺额后SSCS能够弥补电功率缺额的能力,现有文献均未考虑该问题。

可靠性灵敏度可以量化对系统可靠性影响较大的因素[22-23]。文献[24]提出特高压直流(ultra-high voltage direct current,UHVDC)可靠性指标对元件可靠性灵敏度解析表达。SSCS可靠性指标需经多步处理得到,不是底层参数/概率的显式表达,不易直接求导。连续修改参数方法计算量大[25]、效率低。多元函数复合求导方法可以降低计算量[26],用于SSCS灵敏度分析。

本文考虑分层结构和有向指令传输,建立SSCS概率加权有向图模型。该模型不具有布尔特性,在得到邻接矩阵后,采用路径搜索算法提出概率加权全连通矩阵,改进SSCS可靠性指标定义,提出功能可靠性指标。建立SSCS可靠性指标对直流控制参数的灵敏度模型,以降低SSCS失效风险。

1 SSCS的概率加权有向图模型

1.1 三层级SSCS结构

实际SSCS由2～7层站点组成,华中电网SSCS结构如图1所示。

图1 华中电网SSCS结构

SSCS结构主要包括协控总站(master station,MS)、控制主站(main station,MN)和执行站(executive station,EX),如图2所示。图2中:v1～ v4为协控总站;v5～ v16为控制主站;v17～ v34为执行站;e1～ e50为通信通道。v1传送指令至v5、v9、v13,v5传送指令至v17、v19、v21,其余站点指令传送类似分析。v3、v4分别为协控总站v1、v2的异地备用,可防止工作MS失效,主站和备用站间存在信息交互。在电网互联背景下,执行站分别来自不同电网,当电网A发生功率缺额时,利用SSCS向电网B、C发送指令实现功率调节,弥补电网A功率缺额。执行站包括快速响应机组、UHVDC调制、切负荷,其中快速响应发电机组包括抽蓄及储能等。

图2 三层级SSCS

1.2 改进的概率加权有向图

1.2.1SSCS站点可靠性模型

SSCS站点可靠性模型划分为装置、单元、子单元、模件4个层级。SSCS站点由2个互为备用稳控装置组成,稳控装置由主控单元、I/O单元、通信单元组成[11]。以此类推,可建立上下层级间的故障树模型,其中装置至站点故障树模型如图3所示。

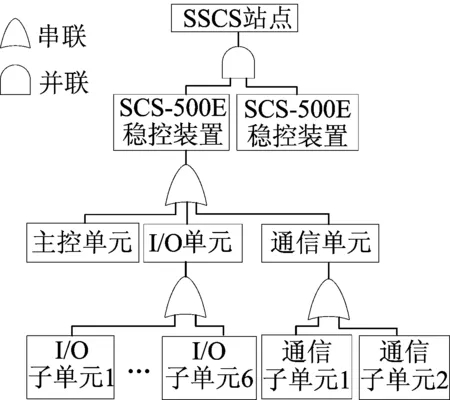
图3 SSCS站点故障树模型

1.2.2 概率加权邻接矩阵

考虑SSCS结构,将其抽象为图G=(V,E),如图4所示。节点集V={vi}表示站点,边集E={eij}表示通道,e13、e14表示协控总站的相互备用关系。E与V间关系由站点与通道连接与否、指令传输方向确定。考虑指令传输具有方向性,G为有向图。

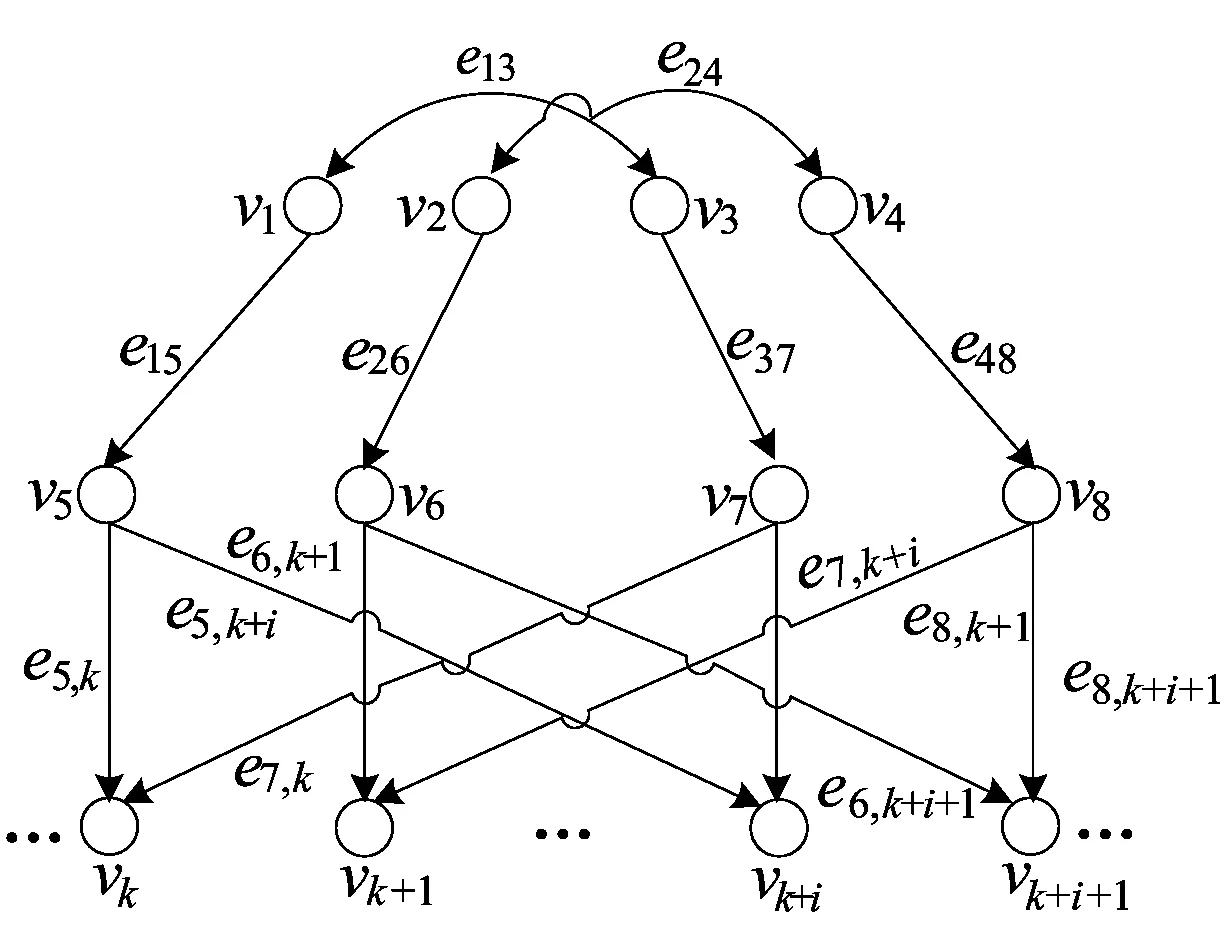
图4 SSCS等效拓扑

若边有权值ωij,则G为加权有向图。从可靠性评估出发,本文取ωij为边eij的可用率aeij,定义G为概率加权有向图(probabilistic weighted directed graph,PWDG)。

将图论应用于电网可靠性评估领域中时,现有文献常常仅考虑边,而忽略顶点[18],这导致结果偏乐观。基于PWDG,定义概率加权邻接矩阵为Dadj,且有:

Dadj(i,j)=aviaeijavj,i≠j且eij∈E

(1)

其中,avi、aeij分别为vi、eij的可用率。相比传统邻接矩阵,Dadj不仅反映了站点间连通性,还反映了站点、通道的随机故障。装置随机故障是其固有属性,可基于长期历史数据统计,受电网运行状态影响较小。

1.3 概率加权全连通矩阵建模

对于分层结构SSCS,指令从MS传送至EX时,经过中间站点。Dadj仅能描述相邻节点间连通概率,不能反映任意两节点间连通情况。基于Dadj,运用全矩阵自乘法、行扫描法、行累加法、改进行累加法,可得到全连通矩阵,但这些算法均基于布尔运算,不适用于SSCS。

以下提出概率加权全连通矩阵Dful。根据拓扑搜索得到vi到vj的路径。定义Dful中元素Dful(i,j)为从站点vi到vj的所有路径连通概率的加权和,即

(2)

其中:αh为站点vi到vj的第h条路径的权重系数;b、c分别为站点vi到vj的第h条路径上的第2个和倒数第2个站点序号。

Dful(i,j)由如下2个因素决定:

1) 站点vi到vj的路径数ni,j。

2) 每条路径上的站点和通道数。

从vi到vj可能存在不止一条路径。为量化第h条路径对SSCS的影响,定义系数αh为:

(3)

其中:nh,MS、nh,MN、nh,EX分别为路径h上协控总站、控制主站、控制子站数量;SMS、SMN、SEX分别为各控制层级重要度,通常取SMS≥SMN≥SEX。αh保证了Dful(i,j)不大于1,便于将Dful用于SSCS可靠性评估。

2 基于PWDG的SSCS功能可靠性评估

2.1 路径可用率

评估SSCS功能可靠性,关键在于评估EX成功执行相应稳控指令的能力,因此需要量化EX接收MS传送下来指令的概率。以下给出由MSvi到EXvj路径的可用率:

Apath(i,j)=Dful(i,j),

ID(i)=1, ID(j)=3

(4)

其中:Apath(i,j)为Apath中的元素,Apath为n1×n3矩阵,n1和n3分别为MS和EX的数量;ID用于标记站点所处层级。当站点位于MS层级时,ID=1;当站点位于MN层级时,ID=2;当站点位于EX层级时,ID=3。

为更直观地表示Apath的含义,给出Dful和Apath间的关系,如图5所示。

图5 Dful和Apath间的关系

图5中,MS→MN表示通信指令由MS传送至MN,其余部分类似定义。

2.2 电网功率缺额

当电网发生严重故障后,有功平衡遭到破坏,可能导致频率失稳。判断能否维持频率稳定时,需要先确定当前电网功率缺额Plost。实际导致Plost原因很多,以下以UHVDC闭锁故障为例进行分析。

初始运行方式下,UHVDC处于双极运行状态,当UHVDC元件随机故障时,如换流阀(CV)、换流变(CT)、控制保护设备(CP)、平波电抗器(smR)、交流滤波器(ACF)、直流滤波器(DCF)、直流线路(DCL)等,会造成功率缺额,由状态空间法可得6状态可靠性模型,如图6所示[24]。图6中,λij、μij分别为从状态i至j的等效故障率和修复率。状态s1～s6定义见表1所列。定义Plost和plost为电网功率缺额及其发生概率,即

表1 UHVDC运行状态

图6 UHVDC输电线路状态空间

Plost=Ps1-Psi,i=2,…,6

(5)

plost=psi

(6)

其中,Psi、psi分别为UHVDC为si状态时的载荷容量和概率。

2.3 功能可靠性指标计算

定义Ω为SSCS状态集合,实际状态x由控制站点、通道、UHVDC运行故障确定,x维数为上述设备状态组合数。由于装置和路径较多,状态空间庞大,以下检验N-1故障。N-1故障表示一个站点或一个通信通道发生故障的情况。区分如下2种情况:① SSCS正常运行时,px=plost;② SSCS发生N-1故障时,定义状态概率px:

(7)

为准确评估SSCS填补功率缺额的能力,定义失效风险RCR和失效功率PCR2个功能可靠性指标,即

(8)

(9)

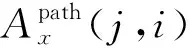
当ΔPx<0时,SSCS中所有EX的可调容量足以填补电网功率缺额,ηx=0,x不统计入RCR和PCR中;当ΔPx>0时,SSCS中所有EX的可调容量不足以填补电网功率缺额,ηx=1,x需要计入RCR和PCR中。

3 SSCS可靠性灵敏度分析

3.1 可靠性指标对SSCS装置可用率的灵敏度

SSCS控制能力由其装置可调容量和可用率决定。前者通常在工程建设初期便已确定,因此以下研究后者对SSCS可靠性的影响。功能可靠性灵敏度用于寻找对SSCS功率平衡能力影响较大的元件和参数。

SSCS装置参数影响系统路径可用率Apath。对系统状态x,ΔPx是系统处于状态x时Apath的函数,受SSCS装置可用率的影响。以avk为例,求PCR对avk的灵敏度,即

(10)

其中:ηx由ΔPx正负决定,取值为0或1;px随功率缺额概率而改变,若SSCS处于N-1故障,px受SSCS故障装置参数影响,则与其他站点和通道无关。因此只有ΔPx是SSCS装置可用率的函数,且只存在于功能可靠性指标PCR中。

3.2 可靠性指标对UHVDC元件参数的灵敏度

功能可靠性指标RCR和PCR体现功率缺额及其发生概率。为量化UHVDC元件故障对SSCS影响,建立可靠性指标对UHVDC元件参数的灵敏度解析模型。故障发生概率plost与UHVDC中直流线路可靠性参数zDC有关。UHVDC和SSCS结构相互独立,px对zDC求偏导,即

(11)

其中:zDC为直流线路故障率λDC或修复率μDC;[]1,i为矩阵第1行第i列元素;Ds为Ts最后一行元素替换为1得到的矩阵;B=[0 … 0 1]T;Ts和Ts′分别为等值前、后的转移率矩阵,且有:

(12)

其中:常数阵M=[m1m2…mh]T表示合并特征。当等值前状态归属于等值后状态i时,mi中对应元素为1,其余元素为0;piE和pIE分别表示等值前、后状态概率对角阵,pIE=MpiEMT。

SSCS功能可靠性指标RCR、PCR是关于系统状态概率px的复合函数,联立式(8)、式(9),RCR、PCR对zDC的灵敏度如下:

(13)

(14)

如果调整稳控站点和通信通道可用率后,SSCS功率缺额风险仍较大,那么可通过改善UHVDC参数、配置备用元件等降低电网频率失稳风险。

4 算例分析

互联电网SSCS站点控制容量分别来自电网A、B、C,其中包括34个站点和50条通道(图2)。SSCS站点和通信线路可靠性参数参考文献[11],UHVDC元件可靠性参数参考文献[23]。

4.1 SSCS功能可靠性评估

在正常运行和N-1方式下计算RCR、PCR,结果如图7所示。图7中,运行方式1～6的功率缺额量分别为0、25%、50%、75%、100%。当UHVDC单极运行时,RCR、PCR占比明显高于其他状况,状态s3概率比s4～s6概率大2～3个数量级。当UHVDC双极运行时,功率缺额量为0。当UHVDC处于3/4双极运行时,SSCS正常运行下RCR、PCR为0,说明控制子站可调容量之和能够填补功率缺额,系统不存在功率缺额风险。相较于处于1/2双极运行状态s4和双极停运状态s6,处于1/2单极运行状态s5时,系统失效功率较大,需要增加可调容量。

图7 不同功率缺额情况下的RCR和PCR

因此RCR和PCR主要受电网功率缺额量和稳控系统可调容量2个因素影响,前者决定RCR、PCR占比,后者影响RCR、PCR具体数值。

4.2 SSCS功能可靠性灵敏度分析

4.2.1PCR对SSCS装置可用率灵敏度

以SSCS正常运行情况为例进行分析,可计算PCR对SSCS装置可用率的灵敏度,结果如图8所示。

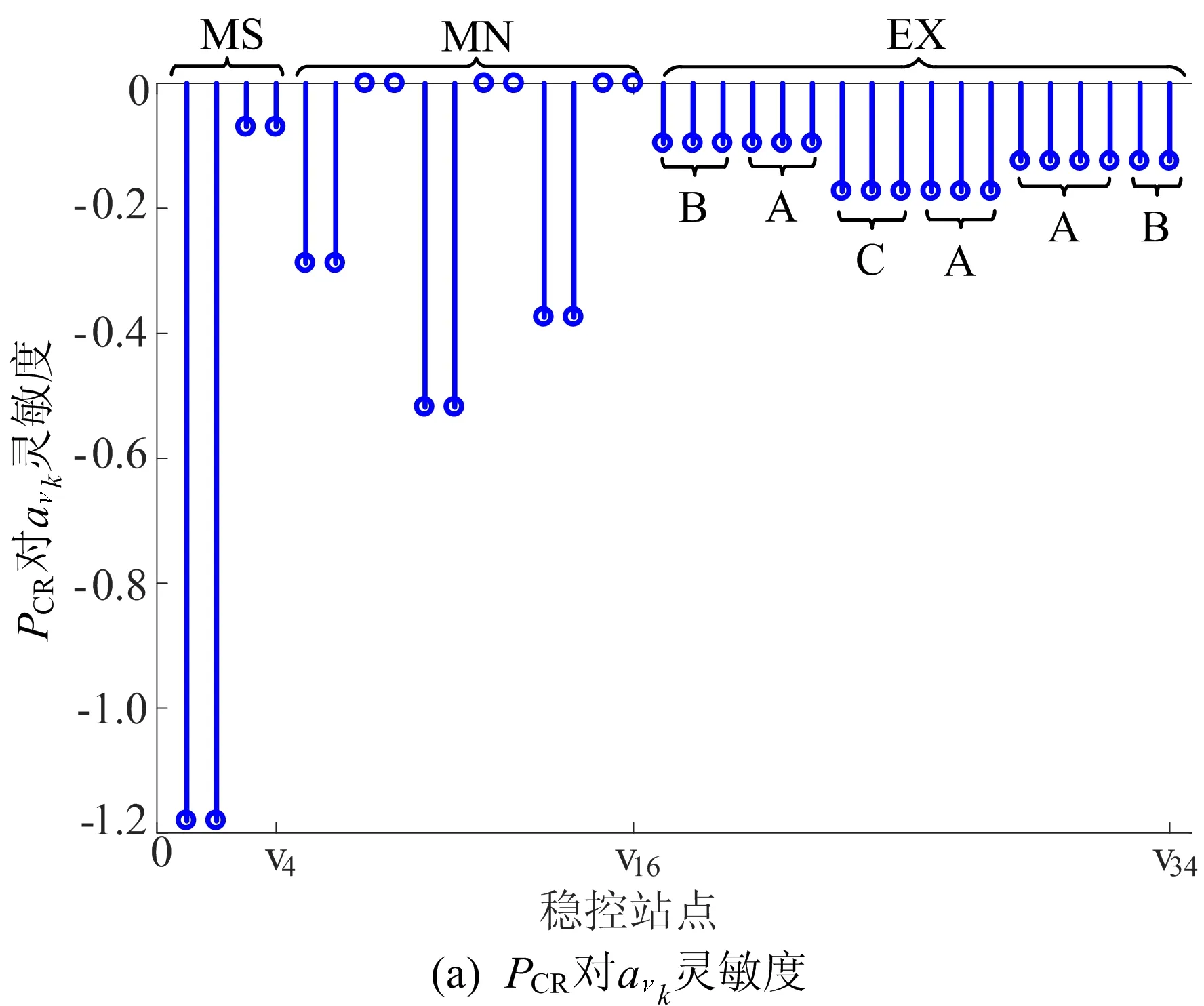
图8 PCR对SSCS装置可用率的灵敏度

图8中,A、B、C表示站点分别来自电网A、电网B和电网C。

从站点来看,协控总站对PCR影响最大,其次为控制主站、控制子站。说明站点层级越高,对系统可靠性影响越大;与越高层级站点相连的通道,对系统可靠性影响越大。

备用协控总站投入前提是原协控总站故障,该事件发生概率极低。因此相对原协控总站,备用协控总站可靠性变化对系统功能可靠性影响不大。

4.2.2RCR、PCR对UHVDC元件可靠性灵敏度

RCR、PCR对UHVDC元件可靠性参数的灵敏度如图9所示。

图9 SSCS功能可靠性指标对UHVDC元件参数灵敏度

RCR对故障率和修复率灵敏度较大,说明UHVDC元件可靠性参数变化更易影响RCR。与其他UHVDC元件相比,smR故障率和修复率变化对SSCS功能可靠性影响较大;RCR、PCR对DCL修复率灵敏度很大。当电网中因UHVDC故障而发生功率缺额时,可以考虑修正smR故障和修复率及DCL修复率改善SSCS功能可靠性。