基于响应曲面法的水力聚结器结构参数优化*
2023-12-04苗春雨蒋明虎赵立新
邢 雷 苗春雨 蒋明虎,2 赵立新,2
(1.东北石油大学机械科学与工程学院 2.黑龙江省石油石化多相介质处理及污染防治重点实验室 3.大庆油田博士后科研工作站)
0 引 言
随着石油资源的不断开发,油田开采已进入中后期高含水阶段[1],大量采出水的举升、处理及运输致使采油经济效益降低,成本急剧增加。在保障石油资源充足的条件下,为提高石油开采的经济效益、降低开采成本,国内外研究学者提出诸多解决方案[2-6]。其中由于旋流分离设备具有体积小、效率高,长期稳定运行等优点[7-8],被广泛应用于油水分离及含油污水处理等相关领域。
1996年水力聚结技术被提出[9],学者们针对聚结器内油滴聚结破碎行为、影响油滴聚结因素、聚结机理等相关问题[10-12]对聚结技术进行了系统研究。GONG H.F.等[13]提出了一种破乳脱水装置,其原理是将高压电场与旋流离心场耦合从而提高性能,结合CFD-PBM的数值模拟方法与试验方法对分离性能进行研究,发现入口流速增加至8 m/s时脱油率提高了6.9%。赵文君等[14]设计了一种聚结-旋流分离装置,通过数值模拟方法对其流场特性进行分析得出了最佳操作参数,当入口油相体积分数为8%、分流比为15%时分离效率可达到最佳值。张津铭等[15]设计了6种不同结构的聚结器,并对聚结性能开展数值模拟分析,得出效果最佳的聚结器结构形式为单出口、单曲线锥,通过该结构聚结后的出口处油滴最大粒径可达到290 μm。赵崇卫等[16]研制了聚结耦合水力旋流组合设备,通过试验结果证明,将差压比控制在1.70时,设备性能可稳定在96%以上,在油田具有较好的应用前景。
上述研究证明了水力聚结技术在油水分离领域的适用性及可行性[17]。邢雷等[18]以出口处油滴的平均粒径为评判标准,对水力聚结器进行结构参数优选,得到了聚结性能最佳的结构参数匹配方案,但利用平均粒径作为聚结效率的评判标准未考虑到其他相关因素。故综合考虑各种因素的影响,本文提出一种新的评判方法,对水力聚结器结构参数开展优化,借助析因筛选设计及响应曲面优化设计,结合数值模拟方法,确定出使聚结性能达到最佳的结构参数值。
1 结构优化及方法
1.1 水力聚结器结构
以油滴碰撞聚结及离心分离原理为基础设计了一种水力聚结器[19-20],结构形式及油滴在旋流场中聚结原理如图1所示。
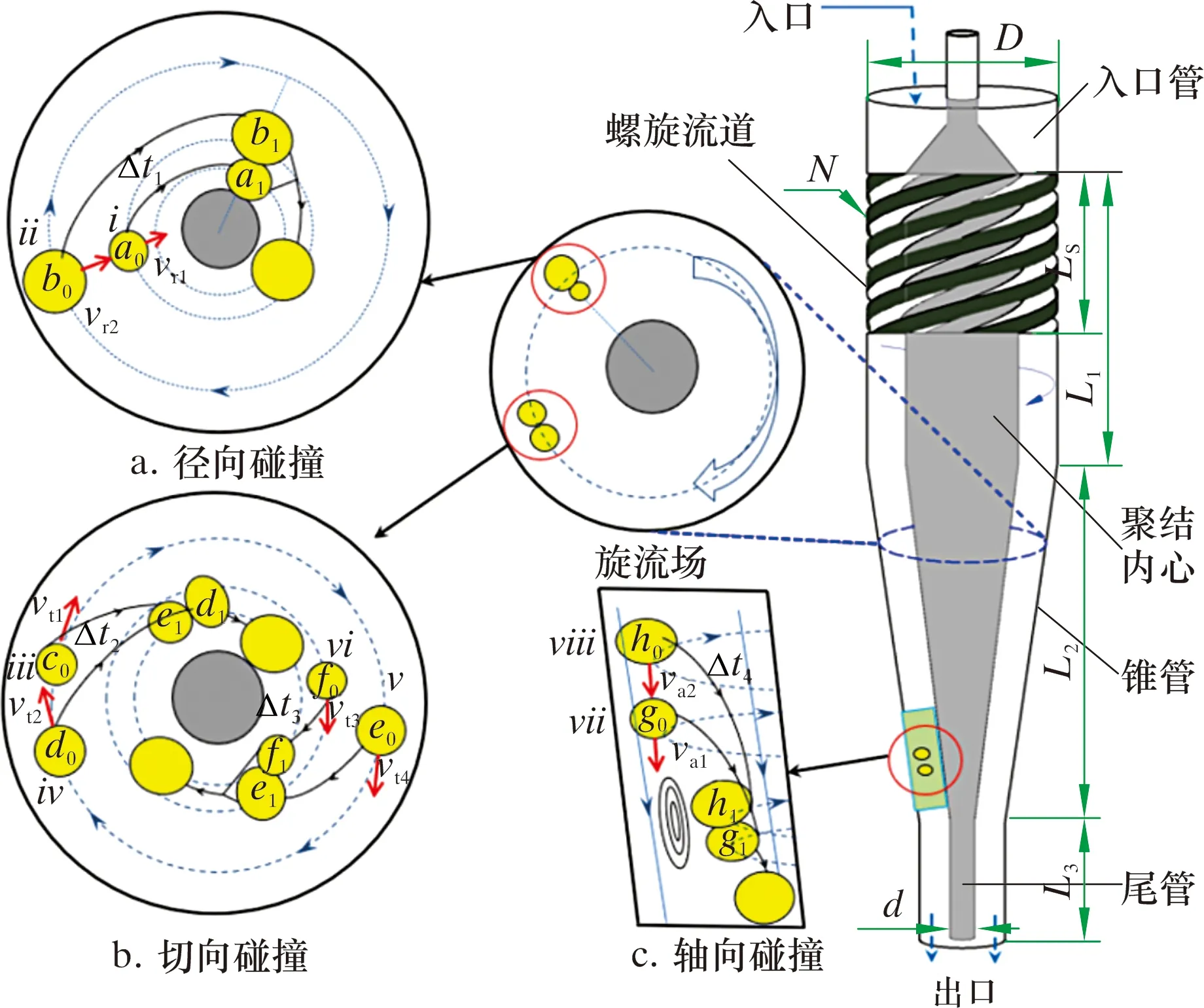
图1 水力聚结器结构及原理图Fig.1 Structure and principle of hydraulic coalescer
其结构主要由入口管、螺旋流道、聚结内心、锥管及尾管组成。其中入口管直径D=120 mm,入口管长度L1=350 mm,锥段长度L2=400 mm,尾管长度L3=80 mm,出口管内径dw=60 mm,聚结内心底径d=15 mm,螺旋流道长度Ls=100 mm,流道角度α=36°、螺旋流道内径Rs=80 mm。其工作原理为:油水两相混合液由入口管轴向进入水力聚结器内部,流经螺旋流道后,混合液由轴向运动转变为切向运动,围绕聚结内心做三维旋转运动,在重力及压力作用下,混合液沿轴向到达尾管处流出。在聚结器内,由于油水两相存在密度差,会使油滴径向迁移至聚结内心处,密度较大的水相沿着边壁向底部运移,离散相油滴在旋流场内部以不同的粒径、运移时间及位置高速运移,使其在旋流场中产生切向、径向及轴向的速度差,从而使油滴间产生不同形式的碰撞聚结,增大混合液中小颗粒油滴的粒径,达到提高后续分离效率的目的。
1.2 试验优化设计
1.2.1 析因筛选设计
由于聚结器结构参数较多,针对所有参数进行系统优化具有一定难度,为减少不必要的试验次数,对其开展结构参数显著性分析,确定出各结构参数对聚结性能影响的显著性高低。目前常用的因素显著性筛选方法主要有序贯分支法、拉丁超立方设计以及析因筛选设计(Plackett-Burman Design,PB)等。由于PB设计可以准确地用最少的试验次数筛选出显著性因子[21],故本文选用PB设计进行水力聚结器结构参数显著性分析,以获得对聚结性能影响显著的结构参数,简化后续聚结器结构参数优化的过程。
混合液由螺旋流道进入聚结器后,轴向运动转变为切向运动,由于入口截面的改变会直接影响混合液入口速度,在不同的入口流速条件下会影响对其他结构参数显著性分析结果的准确性,所以进行显著性分析时不考虑入口结构参数,即保持入口面积一定,针对螺旋流道头数、螺旋流道长度、锥段长度、聚结内心底径以及尾管长度5个结构参数进行显著性分析,以聚结效率为考察指标,确定出对聚结效率影响显著的结构参数。PB试验因素及水平设计见表1。
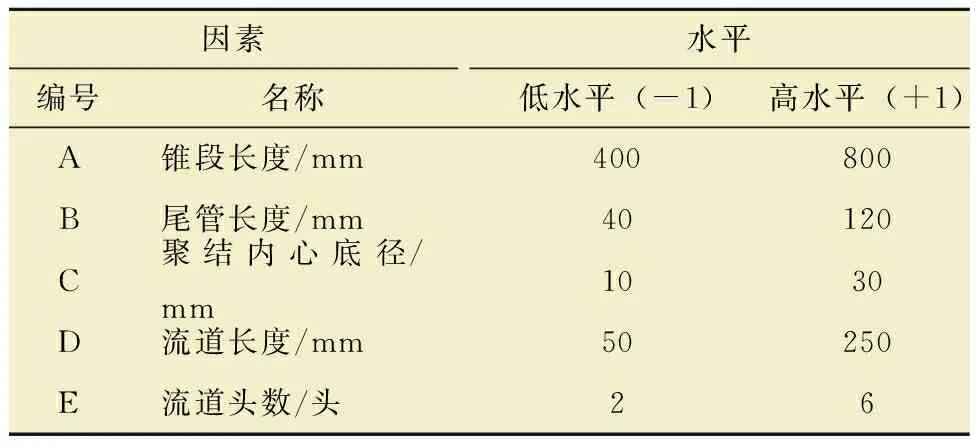
表1 Plackett-Burman试验的因素与水平设计Table1 Factor and level design of Plackett-Burman test
1.2.2 响应曲面设计
响应曲面设计是一种将综合试验设计、数学建模及理论统计相结合的优化方法,通过对研究范围内样本点的集合进行试验设计,拟合出输入变量与响应值的函数关系,得到最优回归方程即设计范围内的最优组合,以达到使响应值处于极值的目的。
中心组合设计(Central Composite Design,CCD)和Box设计(Box-Behnken Design,BBD)是常用的2种响应曲面设计方法,其中BBD每个因素取3个水平,试验所得结果均在设定的水平范围内;CCD每个因素取5个水平,会存在超出原定水平的数据。相对而言BBD试验次数较少,相对经济,且优化出的最佳参数不会因超出最高范围值而导致违背实际工程[22]。故本文采用BBD针对高显著性结构参数,构建显著性结构参数与聚结效率间的回归方程,进而达到结构优化目的。
1.3 数值模拟方法
针对PB设计及响应曲面设计的试验模型,利用ANSYS-Fluent软件采用有限体积法进行数值模拟分析。模拟计算采用多相流混合模型(Mixture),由于旋流场中混合液做三维强旋湍流运动,故湍流模型选用雷诺应力模型(Reynolds Stress Model,RSM)。水力聚结器内主要针对水与油两相介质开展分析,其中将水相(water-phase)设置为连续相,对应密度为998.2 kg/m3,黏度为1.003 mPa·s;油相(oil-phase)设置为离散相,对应密度为850 kg/m3,黏度为1.03 Pa·s,体积分数为2%;将入口边界条件设为速度入口,入口速度为0.41 m/s;出口边界条件设为自由出口。采用标准壁函数法边界条件,动量、湍动能和湍流耗散率为二阶迎风离散格式,收敛精度设为10-6。采用的压力-速度耦合算法为SIMPLE算法,选用压力基准算法隐式求解器稳态求解,壁面采用无滑移、不可渗透边界。
2 聚结效率评判方法
关于聚结效率的计算方法大多采用2种表述形式,一种是微观上以液滴间液膜的形态计算,即液滴间产生相互碰撞,发生表面接触到液膜破裂液滴聚结所用的时间来评判聚结效率;另一种是宏观上通过出口及入口处油滴粒度分布情况分析聚结程度。对于定量评价聚结性能仅仅依靠对比入口及出口处平均粒径的方法,不能仅由平均粒径单因素评判聚结性能的好坏,应考虑最大油滴尺寸、最大油滴数量或体积占比、最小油滴尺寸、最小油滴数量或体积占比、平均粒径等多种相关因素,具体计算方法[23]:
(1)
式中:Ec为聚结效率;ζ为聚结系数;D(xoutlet)为聚结器出口处油滴粒径分布曲线的积分值。
(2)
其中:D(xinlet)为聚结器入口处油滴粒径分布曲线的积分值。
(3)
式中:domax、domin分别为出口处最大粒径和最小粒径,μm;dos为出口处平均粒径,μm;dimax、dimin分别为入口处最大粒径和最小粒径,μm;dis为入口处平均粒径,μm;f(xoutlet)为聚结器出口油滴粒径分布函数;f(xinlet)为聚结器入口油滴粒径分布函数;Dideal为理想粒径值。
Dideal的定义为假设由聚结器入口进入到聚结器内的油相到出口处时,全部聚结成为一个大的球形油滴,这个大球形油滴的粒径值即为理想粒径。设出口处油滴粒子数变为1时,即所有油滴均汇聚成为一个球形油滴时的聚结效率为100%,则出口处球形油滴体积为:
(4)
通过该体积V值可以求出效率为100%时的油滴直径,定义该油滴直径为理想粒径,计算方法为:
(5)
式中:mi为聚结器入口油的质量,kg;ρo为油相密度,kg/m3。
聚结系数ζ是由最大粒径系数ømax、最小粒径系数ømin、粒径频数系数λ、粒径占比η及修正系数ε等组成,其表达式为:
ζ=ømax+0.1ømin+λ+η-ε
(6)
最大粒径系数为:
ømax=0.000 1dimax
(7)
最小粒径系数为:
ømin=0.000 1dimin
(8)
粒径频数系数为:
(9)
式中:ninlet为入口粒径频数;noutlet为出口粒径频数。
最大粒径占比计算方法为:
(10)
式中:nmax为最大粒径频数。
修正系数ε是当聚结器出口处油滴个数为1时,调节聚结系数ζ的值为0,修正系数ε表达式为:
(11)
最终得出聚结效率计算方法为:
eømax+0.1ømin+λ+η-ε×100%
(12)
3 结果分析
3.1 基于PB设计的显著性分析
将PB设计的12组试验数据结果进行统计分析,得出各因素对考察指标聚结效率影响的显著性对比,结果如表2所示。
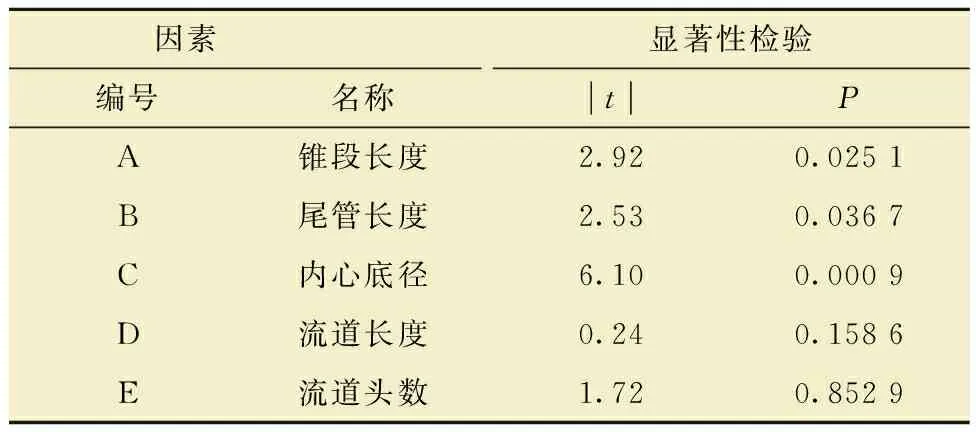
表2 试验结果的显著性检验Table 2 Significance test of test results
其中|t|值表示显著性水平的高低,|t|值越大表示该因素对考察指标的显著性越高;P值为样本间的差异由抽样误差导致的概率,P>0.05表示该因素与指标间无显著意义;P≤0.05表示该因素与指标间有显著意义,而P<0.01表示两者有极显著意义。由表2分析得出,各因素显著性顺序由高到低依次为C>A>B>E>D。通过图2所示的5种结构参数对聚结效率影响显著性帕累托图可更直观地判断出显著性高低。
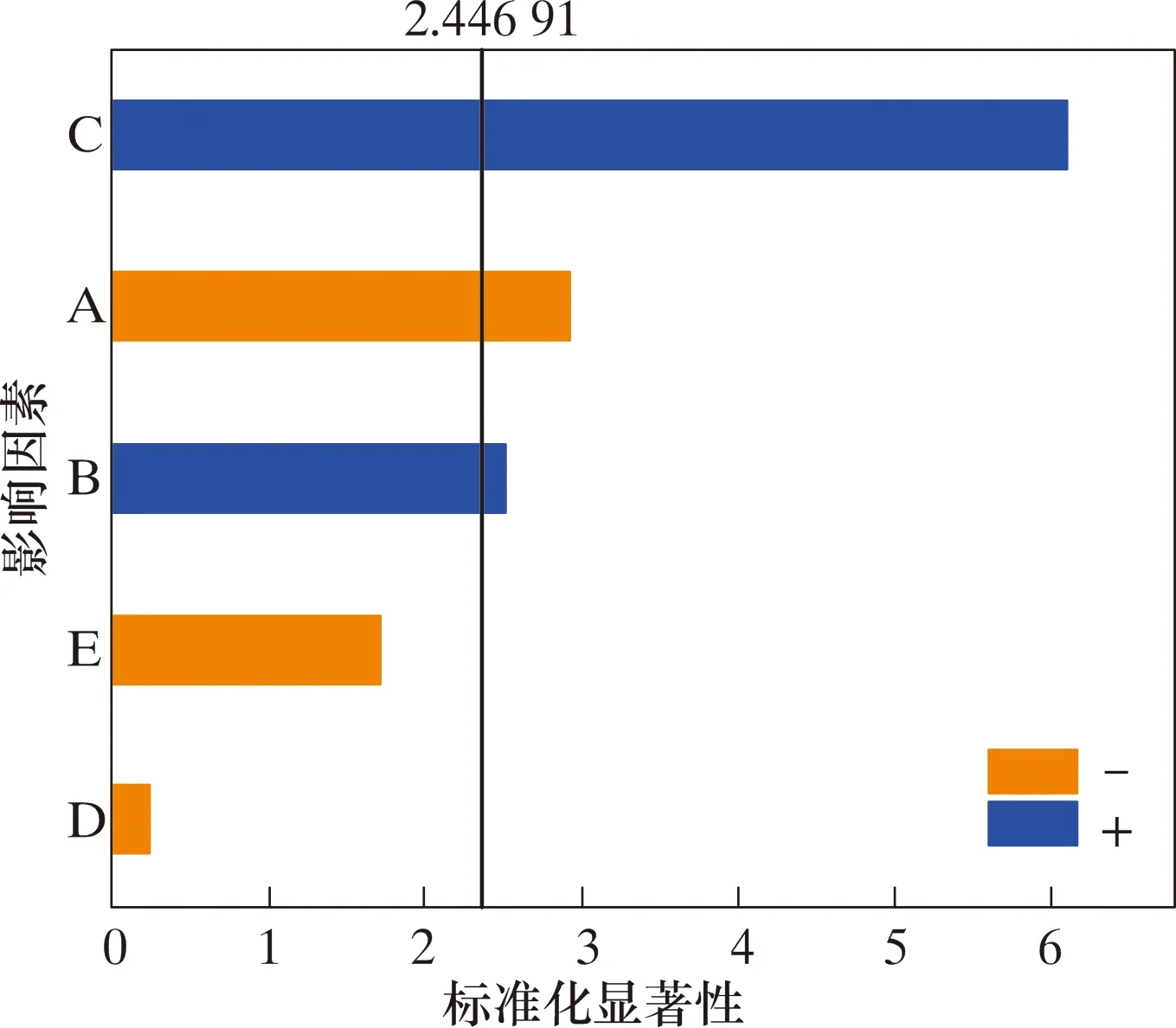
图2 各因素对期望值影响的帕累托图Fig.2 Pareto diagram for the impact of factors on expected values
图2中各因素对应的条形图长度可以明显反映出对聚结效率影响的显著水平,黑色竖线代表95%的置信区间,超出该线表示因素对考察指标影响显著。通过综合分析确定出高显著性结构参数为锥段长度、尾管长度以及内心底径。
3.2 基于响应曲面设计的聚结效率回归方程
PB设计筛选出3个显著性较高的结构参数,故将响应曲面设计因素设置为3个,各因素水平取值如表3所示。

表3 因素水平设计Table 3 Factor and level design
本次设计共形成17个试验组,其中中心试验重复次数为5,因变量为聚结效率值Ec。BBD试验设计及数值模拟结果如表4所示。
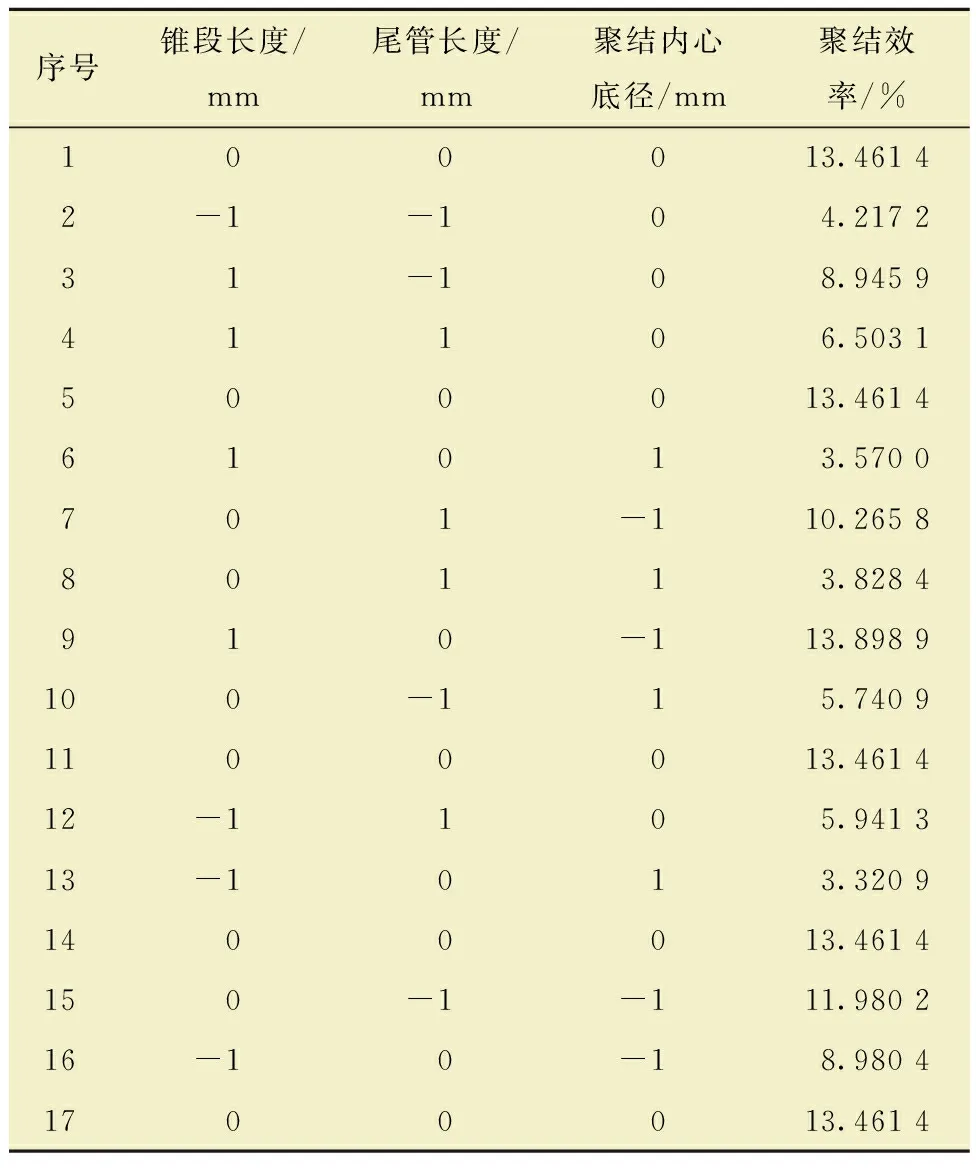
表4 BBD设计及试验结果Table 4 BBD design and test results
采用二阶多项式模型对表4结果进行多项式拟合,通过多元线性回归分析得出锥段长度、尾管长度以及聚结内心底径与响应目标间的多元二次回归方程:
Ec=-1.285 6+1.578 2x1+0.017 7x2+
0.009 1x3-2.604 4×10-6x1x2-
5.836 7×10-6x1x3-2.477 6×10-6x2x3-
(13)
式中:x1、x2、x3分别为锥段长度、尾管长度和聚结内心底径。方程中的正负系数反映了各因素与响应值之间的关系,正系数表示响应值随因素增加而增大,负系数表示响应值随因素增加而减小,根据回归方程可知聚结效率随各因素的增加呈减小趋势。对回归方程进行方差分析,分析结果如表5所示。F值越大、P值越小表示模型的相关系数越显著。
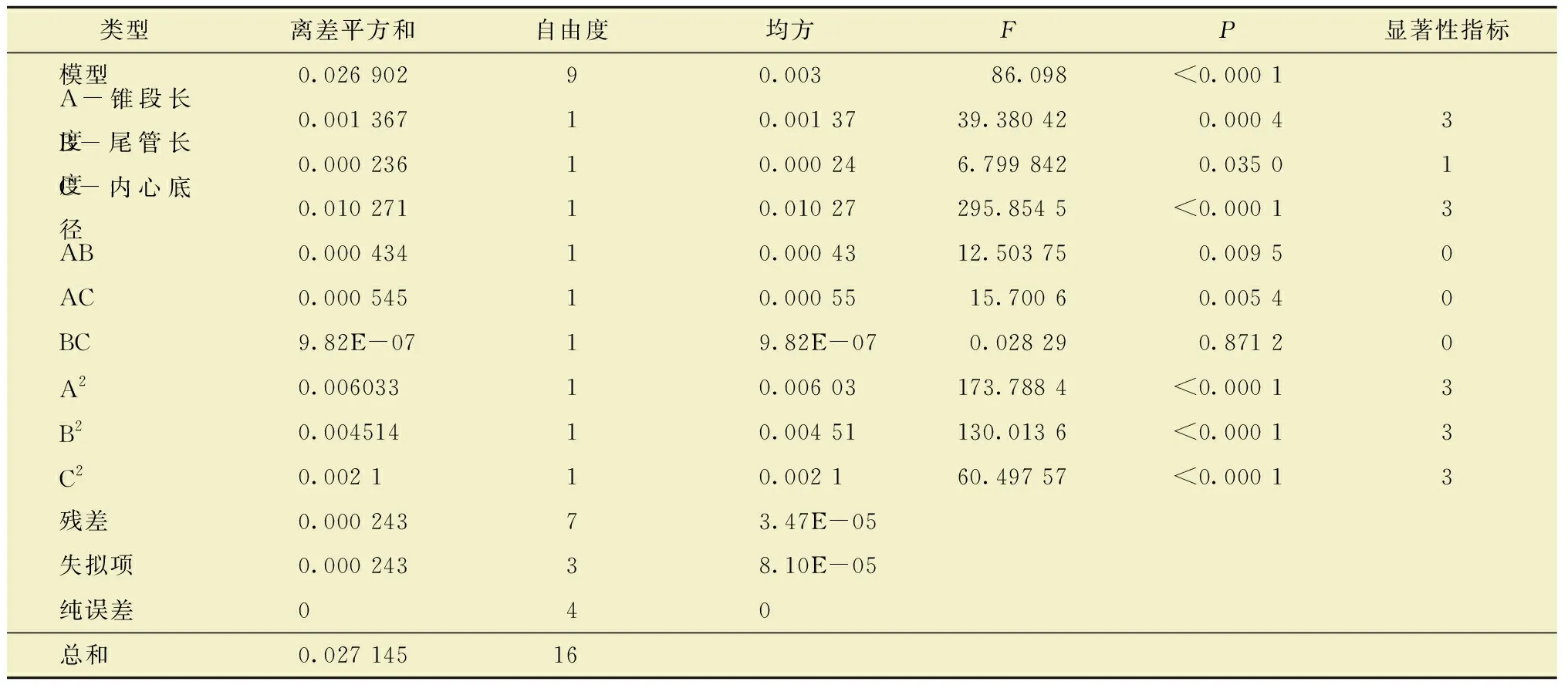
表5 回归模型的方差分析结果Table 5 Variance analysis results of regression model
由表5可知,模型的P值小于0.000 1,F值为86.098,说明各因素在水平范围内变动时,可用构建的回归方程对聚结效率进行预测且预测值具有较高的准确性。
3.3 响应关系分析
图3所示为2种不同结构参数间的交互作用对聚结效率影响的三维响应关系曲面及等高线图。
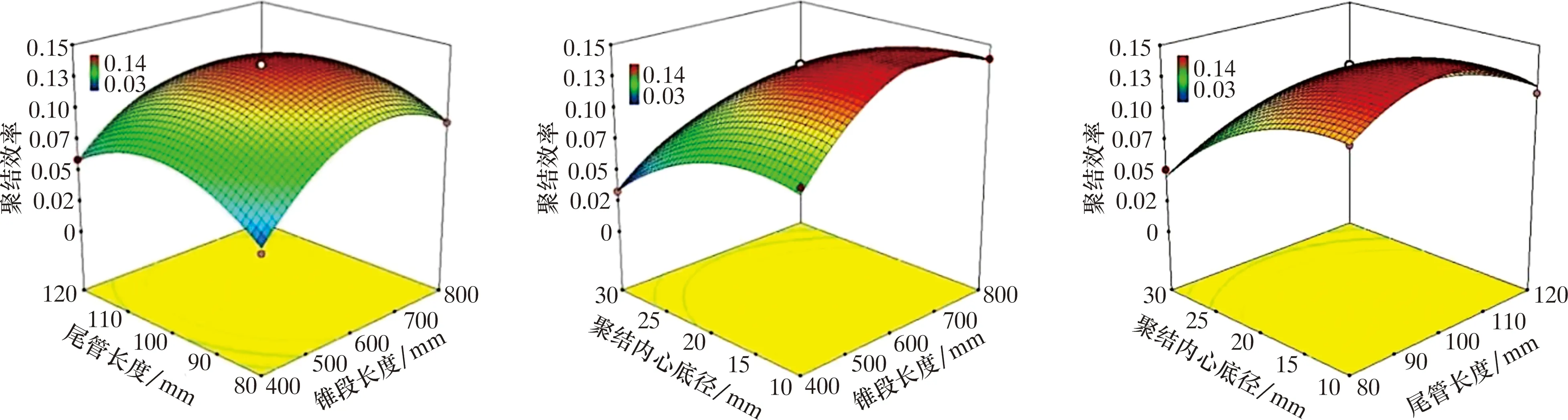
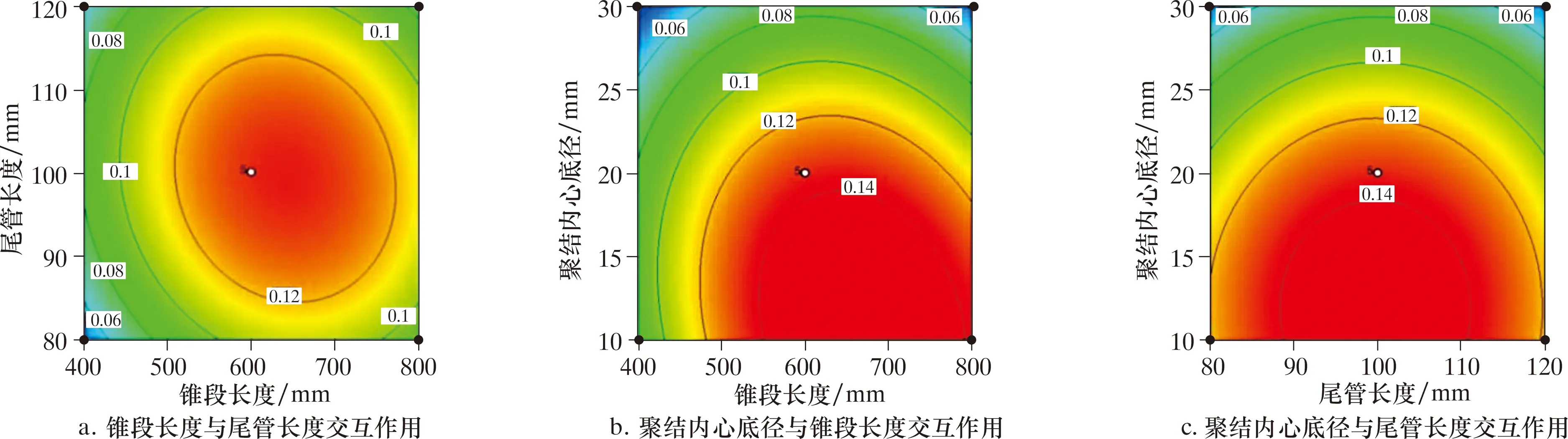
图3 不同因素间交互作用对聚结效率影响的响应面及等高线图Fig.3 Response surface and contour maps for the impact of interaction between different factors on efficiency
图3a显示了尾管长度和锥段长度的交互作用
对聚结效率的影响。由图3a可看出,增加尾管长度,聚结效率呈现先增大后减小的趋势。三维响应曲面呈现山谷状,说明在其范围内存在可使聚结效率处于极大值的参数值;等高线图的投影结果呈圆形,说明尾管长度与锥段长度之间的交互作用对聚结效率影响不显著。
图3b显示了聚结内心底径与锥段长度之间的交互作用对聚结效率的影响。图3b反映出当增加聚结内心底径时聚结效率呈减小趋势,当增加锥段长度时聚结效率先增大后减小;等高线图的投影呈椭圆形,表明聚结内心底径与锥段长度之间的交互作用对聚结效率的影响显著,且响应曲面回归模型中x1x3的系数是所有交互作用项中最大的,说明聚结内心底径和锥段长度的交互作用对聚结效率的影响比其他两组作用影响更显著。
图3c显示了聚结内心底径与尾管长度之间的交互作用对聚结效率的影响。由图3c可知,聚结效率随着聚结内心底径的减小呈增大趋势,而随着尾管长度的增加,聚结效率呈先增大后减小趋势;等高线图的投影呈现圆形,说明聚结内心底径与尾管长度之间的交互作用对聚结效率影响不显著。
3.4 最优结构聚结性能验证
通过对结构参数与聚结效率间的多元二次回归方程进行最小二乘法偏微分求导,可得出使聚结效率处于极大值的结构参数匹配方案,即在研究范围内的最佳结构参数点。计算得出优化后的聚结器结构参数分别为锥段长度为678.63 mm,尾管长度为99.89 mm,内心底径为10 mm。
为验证最佳结构参数的可行性,依据最佳结构参数值构建聚结器模型,计算模型及边界条件与初始结构保持一致,得出优化后聚结器的聚结效率,完成优化前、后聚结效率对比分析,结果如表6所示。优化前、后聚结器结构对比如图4所示。
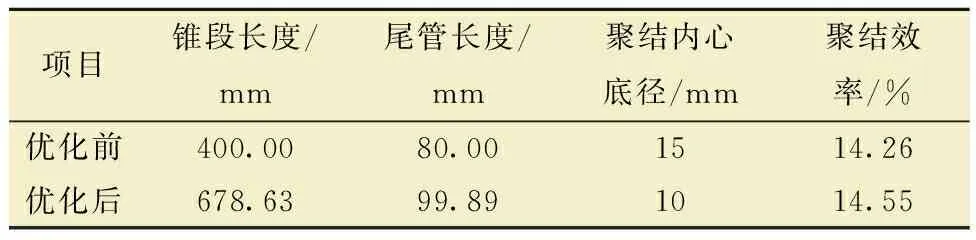
表6 优化前、后结构参数及聚结效率对比Table 6 Structural parameters and coalescence efficiency before and after optimization
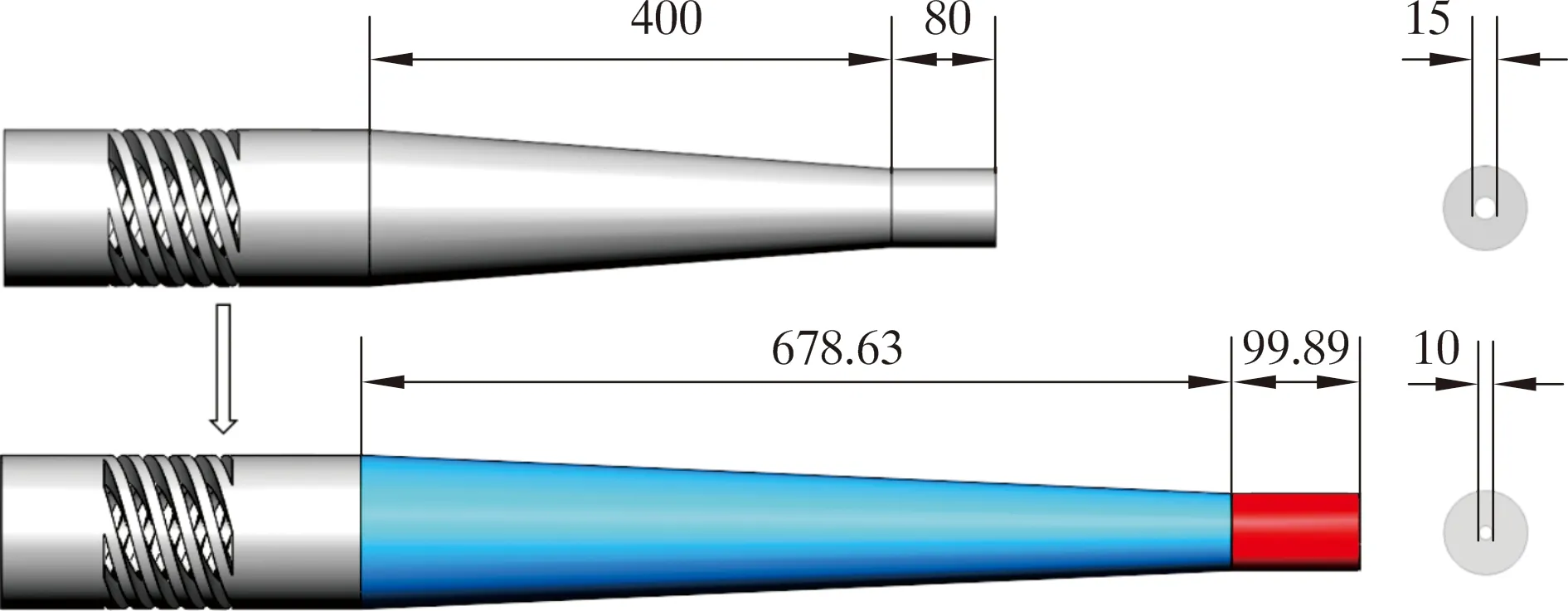
图4 优化前、后结构变化示意图Fig.4 Schematic diagram of structural changes before and after optimization
将优化前、后聚结器对应的油滴粒径分布进行对比分析,结果如图5所示。由图5可知,优化后聚结器出口截面处油滴的平均粒径由524.7 μm增大至550.9 μm;优化前聚结效率为14.26%,优化后聚结器的效率增加至14.55%,且油滴的最大粒径也明显增大。对比充分验证了优化后聚结器的可行性及高效性,同时也证明了构建的结构参数与聚结效率间回归方程的可靠性。
4 结 论
(1)综合考虑了最大油滴粒径尺寸、最大粒径油滴体积占比、最小油滴粒径、最小粒径油滴体积占比以及平均粒径等多种相关影响因素,形成了一种适用于单入口及单出口聚结器的聚结效率评判方法。
(2)针对水力聚结器的5个主要结构参数,利用PB设计,确定出显著性较高的参数及顺序依次为锥段长度L2、尾管长度L3以及聚结内心底径d。针对高显著性结构参数利用响应曲面设计进行结构参数优化,得出最优回归方程,确定出最佳结构参数值为锥段长度678.63 mm、尾管长度99.89 mm、内心底径10 mm。
(3)针对优化前后的水力聚结器,在相同工况条件下开展聚结性能验证。结果表明,优化后聚结器出口处平均粒径由524.7 μm增加至550.9 μm,聚结效率由14.26%提高至14.55%,聚结性能得到明显提升。
