基于深度学习的油气管道变形管段识别方法*

2023-12-04马林杰马如隆宋鑫灿

石油机械 2023年11期

王琳马林杰徐建马如隆宋鑫灿

(西南石油大学机电工程学院)

0 引言

长输油气管道的敷设地形复杂，腐蚀、人为活动、长期的地壳运动等会导致管道在局部管段产生较大的弯曲变形，造成应力集中，严重时甚至会导致运输物质的泄漏，造成环境污染和经济损失，威胁人们的生命[1-3]。目前，管道全线弯曲变形检测主要是通过搭载惯性测量单元(Infertial Measuremeut Unit，IMU)的管道内检测方式来实现。理论上，弯曲应变值的大小反映了管道的弯曲程度，但实际应用中，真实的外力弯曲和凹陷、弯头、焊缝等局部的管道变形特征在IMU检测信号上存在一定的相似性，如何高效且准确地识别这些变形特征是管道IMU检测数据分析的重要环节。

目前，基于IMU检测数据的变形管段识别方法主要分为2类，分别是传统的数据特征统计方法和机器学习方法。LI R.等[4-5]通过姿态角计算管道全线的弯曲应变，选取弯曲应变阈值识别弯曲变形管段，并通过试验验证了该方法的有效性。H.SATO等[6]通过陀螺仪输出角速度在经过管道弯头时会出现急剧的变化来识别管道的弯头。管练武[7]分析发现，IMU加速度信号在通过焊缝时会出现波动，可以据此识别管道的焊缝位置。刘啸奔等[8-9]采用不同管段类型的应变曲线统计特征和热力图作为机器学习模型的输入，实现了不同变形类型的分类。现有的方法已经证明了IMU检测在变形管段识别中的可行性，但无论是数据统计还是机器学习都不可避免以下2点：①需要从连续的IMU检测信号中筛选变形管段信号；②需要选定合适的参数作为分类的指标或者机器学习的输入。

近年来深度学习迅猛发展，其强大的特征提取和特征融合能力，在自动提取与学习时序数据多元数据特征上显示出巨大优势[10-13]。本文构建了深度学习网络以解决油气管道全线变形管段识别问题，将深度学习中时序信号分类的方法应用于管道IMU检测数据识别，避免了数据筛选和特征提取，可以有效识别和分类变形管段，可为油气管道全线变形管段识别提供一种高效可行的方法。

1 方法介绍

1.1 弯曲应变计算

管道全线的弯曲应变由曲率来计算，它反映了管道在一段里程上的弯曲程度。弯曲应变为管道半径和曲率半径的比值，计算公式如下[14]：

(1)

(2)

(3)

(4)

(5)

式中：kv、kh、k分别为垂直曲率、水平曲率和总曲率，rad/m；εv为垂直应变，rad；ε为弯曲应变，rad；D为管道内径，m；θ为俯仰角，rad；Δθ为俯仰角差值，rad；Δψ为航向角差值，rad；Δs为里程差值，m。

1.2 输入数据截取

理论上，经曲率计算得到的弯曲应变结果直接反映了管道的弯曲程度。但在实际应用中，当管道内检测器通过焊缝、弯头及凹陷等管段时，内检测器的姿态会发生不同程度的变化，进而导致陀螺仪输出角速度及由姿态计算得到的弯曲应变值发生不同特征的改变，因此，角速度和管道全线弯曲应变值可以作为特征识别的有效输入。总的弯曲应变值同时反映管道在竖直方向和水平方向的弯曲，但经过凹陷管段时的变化主要体现在垂直应变分量上，三轴角速度中的ωy主要反映内检测器在管道内运行时自身的转动。

综上所述，选择ωx、ωz、垂直应变分量、总的弯曲应变四维数据作为模型的输入、采用滑动窗口的方式来提取输入数据，如图1所示。

沿里程平移固定长度的窗口来截取输入信号，主要参数有窗口的长度及每次的平移步长。

1.3 卷积神经网络

卷积神经网络(Convolutionel Neural Network，CNN)通常有5层：输入层、卷积层、激活层、池化层和全连接层。其中，一维卷积网络常被用于处理时间序列，卷积层通过卷积核提取输入信号的特征；池化层可以减少参数并简化计算量；全连接层用来对提取的特征进行分类[15]。卷积运算的数学表达式如下：

(6)

式中：k、b表示第l层i个神经元的权置和偏置；x为j层的第l个输入。

池化层通常在卷积层后用来选择和过滤提取的特征，池化层的表达式为：

(7)

式中：q为第i个通道上l个神经元；W为池化的核大小。

1.4 双向长短期记忆网络

循环神经网络(Recurrent Neural Network，RNN)以序列数据为输入，强调序列信号前后的关联，可有效地对时序信号进行处理[16]。但RNN不具有选择功能，容易出现梯度消失和梯度爆炸。长短期记忆神经网络(Long Short-Term Memory，LSTM)是循环神经网络的改良，具体来说，它是在RNN的基础上引入了记忆单元，具体包括遗忘门、输入门和输出门。LSTM单元的基本结构如图2所示[17-18]。

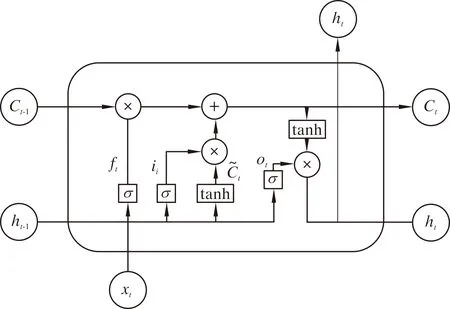
图2 LSTM单元Fig.2 LSTM unit

BiLSTM(双向长短期记忆网络)由2层LSTM网络组成，每层网络都有输入序列，但以相反的方向传输信息，即正向LSTM和反向LSTM[19]。将从正反方向提取的2个隐藏状态向量连接起来，以综合前后信号的特性。

1.5 评价指标

采用式(8)～式(11)对分类模型的准确性、精确率、召回率和F1分数进行评估。其中TP、TN、FP和FN分别为真阳性、真阴性、假阳性和假阴性。

准确率PA表示分类的总体正确性：

(8)

精确率PP是指正确分类的比例：

(9)

召回率PR表示实际阳性被正确分类的比率：

(10)

F1分数FS可以看作是模型的精确度和召回率的组合：

(11)

2 基于CNN-BiLSTM管道变形识别

2.1 CNN-BiLSTM

BiLSTM网络可以更好地捕捉输入信号双向的时序特征，但在空间维度上感知能力差，而卷积层具有较好的空间感知能力，将2种模型的优势相组合用于管段类型分类，可充分利用模型在空间和时域上的提取能力。构建的CNN-BiLSTM网络结构如图3所示。

图3 CNN-BiLSTM网络结构Fig.3 Structure of CNN-BiLSTM

2层卷积层被用来提取输入数据的特征，特征提取后的数据被输入BiLSTM层，学习输入特征在前后顺序上的关系[20]。之后，BiLSTM的输出将作为全连接层的输入并通过Softmax函数实现管段类型分类。

2.2 识别流程

基于IMU检测的管道全线变形管段特征识别方法整体流程如图4所示。通过清管器搭载IMU测量得到清管器在油气管道全线运行的姿态信息，根据弯曲应变计算公式计算里程间隔上管道全线的弯曲应变值，对角速度和弯曲应变进行归一化处理，采用里程滑动窗口截取归一化后的角速度和弯曲应变值。之后，截取的数据将作为CNN-BiLSMT模型的输入，被送进网络模型学习其潜在的规律。最后，通过全连接层和Softmax分类器对输入的类型进行分类，得到该段管段的类型。通过滑动窗口提取管道不同管段的输入信号可实现全线管道变形特征的识别。

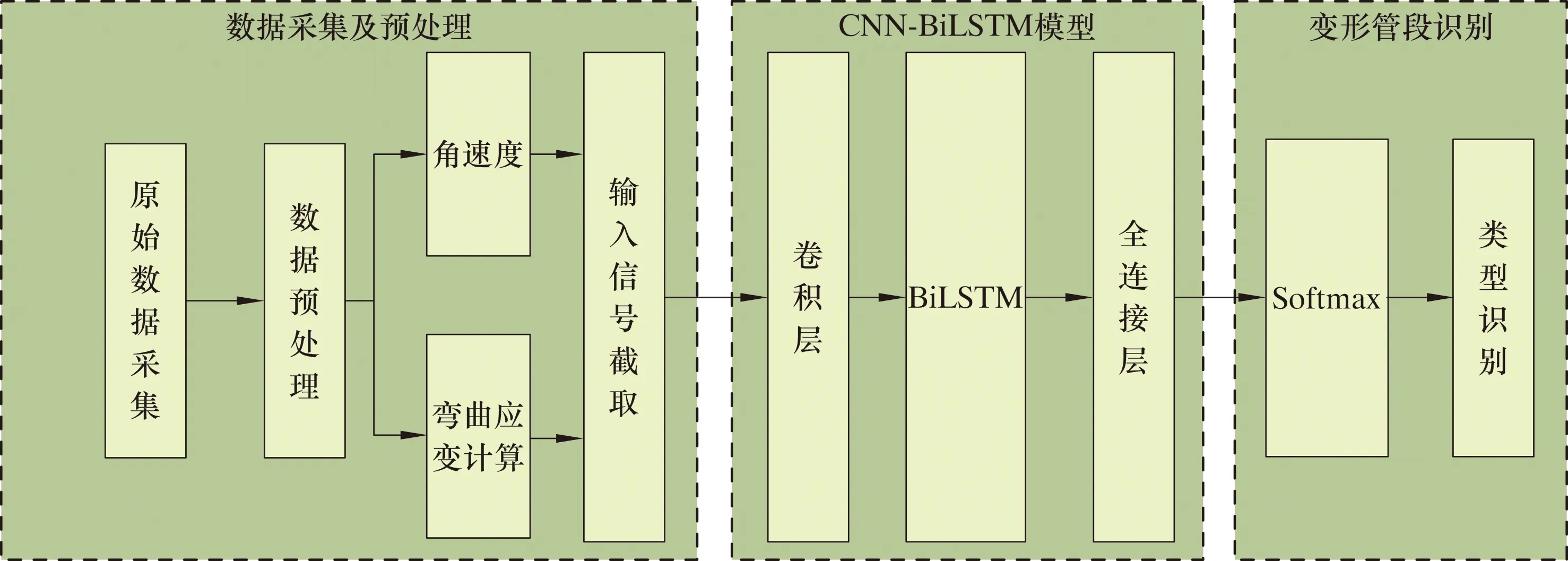
图4 管道形变管段识别方法Fig.4 Identification method for pipeline deformation sections

3 应用分析

利用现场实测IMU 200 km数据来制备管段类型数据集，以验证所提方法的正确性。角速度信号及计算得到的垂直应变和弯曲应变10 km部分数据如图5所示。弯曲应变的计算里程间隔取0.05 m。

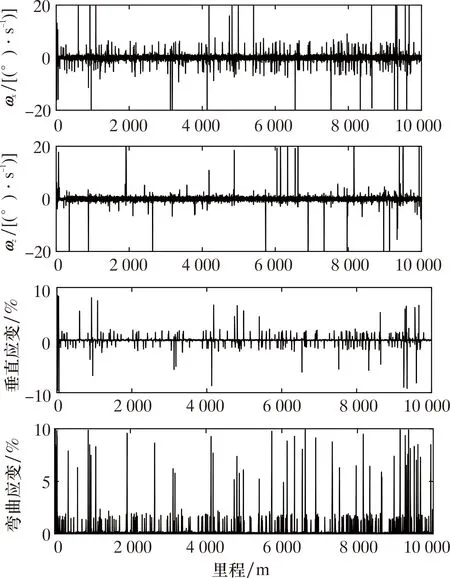
图5 10 km管道实测角速度和弯曲应变Fig.5 Measured angular velocity and bending strain of a 10 km pipeline

3.1 不同管道特征数据

在管道IMU检测数据中，能够体现管段类型的主要有直管、焊缝、冷弯、热弯、弯曲变形和凹陷共计6类。检测器在直管中运行时，弯曲应变的值较小且波动小，如图6a所示；焊缝处的弯曲应变为小范围内的局部凸起，如图6b所示；管道内检测器通过弯头时，弯曲应变会在一个管节内出现急剧的变化，热弯和冷弯的区别主要体现在峰值上，如图6c、图6d所示；弯曲变形管段弯曲应变的均值超过了0.125%，且持续的里程较长，超过了1个管节长度，如图6e所示；凹陷处的垂直应变一般呈下凹状，应变的大小受凹陷程度和内检测器长度影响，如图6f所示。综上所述，内检测器在不同管段运行时弯曲应变值会出现不同特性的变化，变化的幅度和长度取决于内检测器在通过不同管道特征时的姿态变化情况。

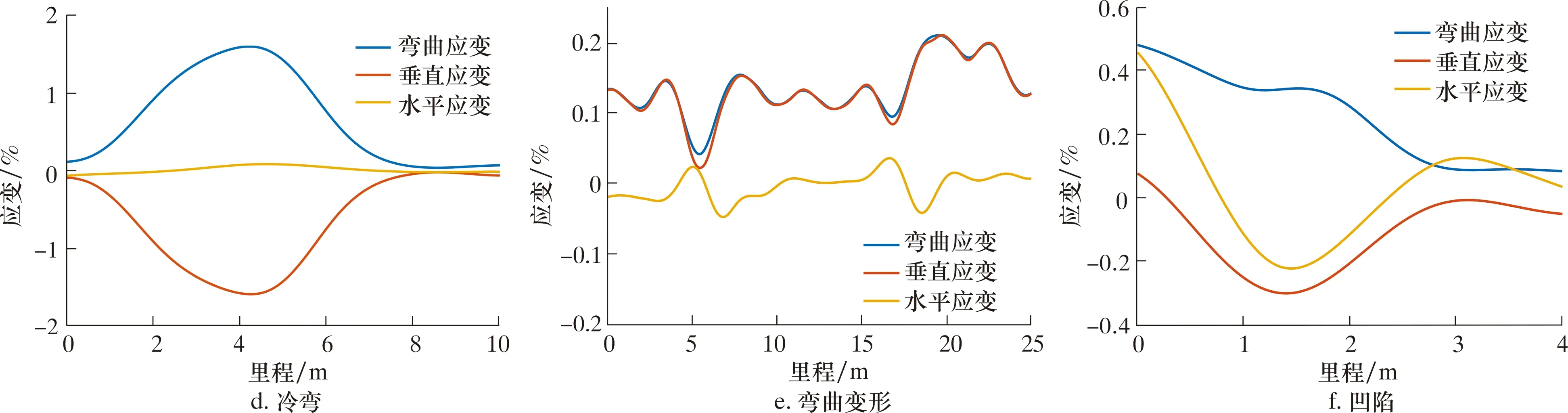
图6 不同管段类型弯曲应变数据特征Fig.6 Bending strain data characteristics of different pipe section types

3.2 标签及数据集准备

信号截取窗口长度为6 m，步长为0.1 m。除6种单独的管段类型外，滑动窗口不可避免地会截取到混合的管道类型。因此，样本标签除6种单独类型外，还包含了4类常见的混合类型。管道IMU检测数据中，直管、焊缝、弯头的数据量远多于弯曲变形、凹陷的数据量，在制作数据集时为避免模型过拟合，需要保证每种类型数据量相差不能过大。因此，对于较多的数据样本随机地选取部分数据，最终制备了包含10种管段类型共81 565份数据的数据集。

不同标签对应的类型及数据量见表1，不同管段类型在四维数据上的分布特征见图7。

表1 不同标签对应的类型及数据量Table1 Types and data volume for different labels

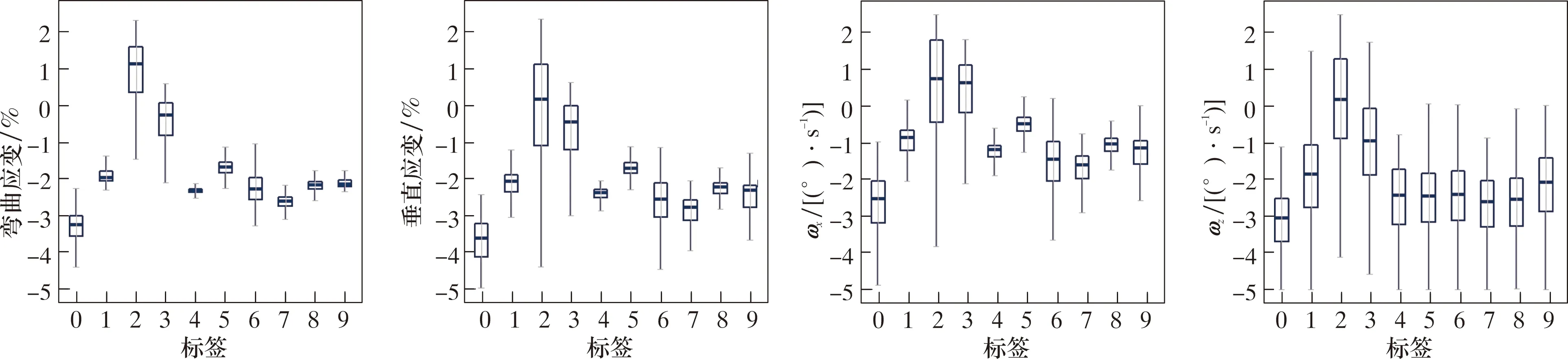
图7 不同管段类型在输入参数上的分布Fig.7 Distribution of different pipe section types on input parameters

3.3 模型参数及训练过程

表2是网络模型每层对应的超参数设置，模型在Pytorch框架下搭建。学习率为0.001，损失函数为交叉熵损失，Batchsize(批次大小)设置为128，输入数据通过最大最小值归一化处理，每层超参数对应的数值为：卷积层(通道数，卷积核大小，步长)，最大池化层(池化核大小，步长)，Dropout层(丢弃率)，BiLSTM层(输入维度，输出维度)，线性层(输入维度，输出维度)。

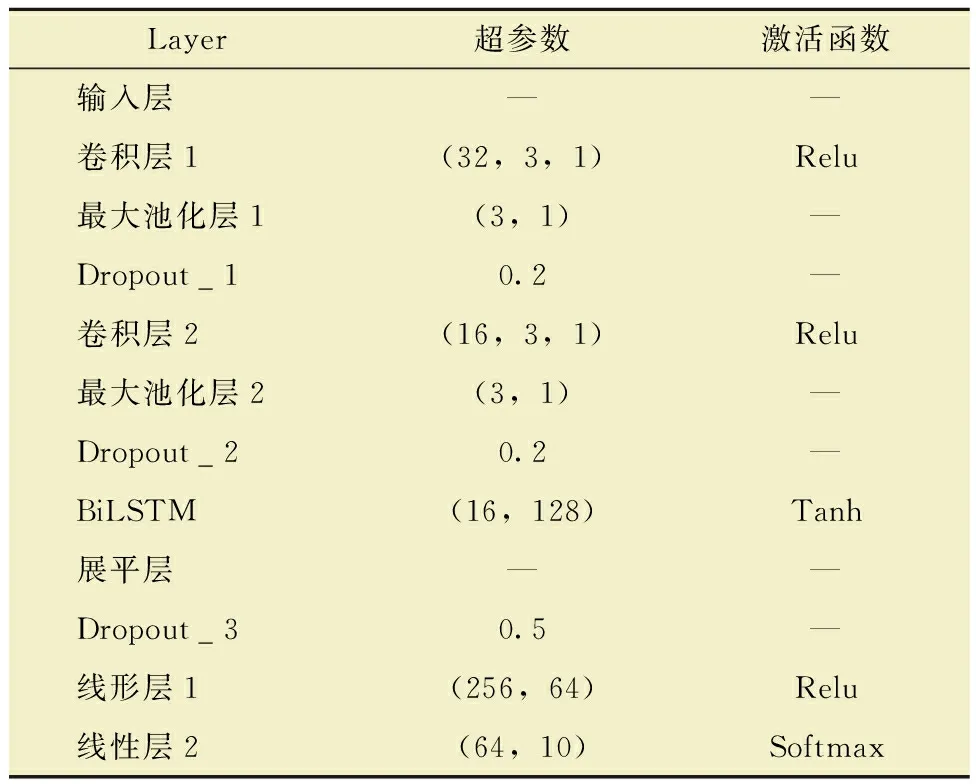
表2 模型超参数设置Table2 Hyperparameter setting of network model

按8∶2的比例将数据集分为训练集和测试集，模型的训练过程如图8所示。由图8可知，预测准确率逐渐提高，损失逐渐减小，当训练次数大于200次后，模型的训练趋于稳定。

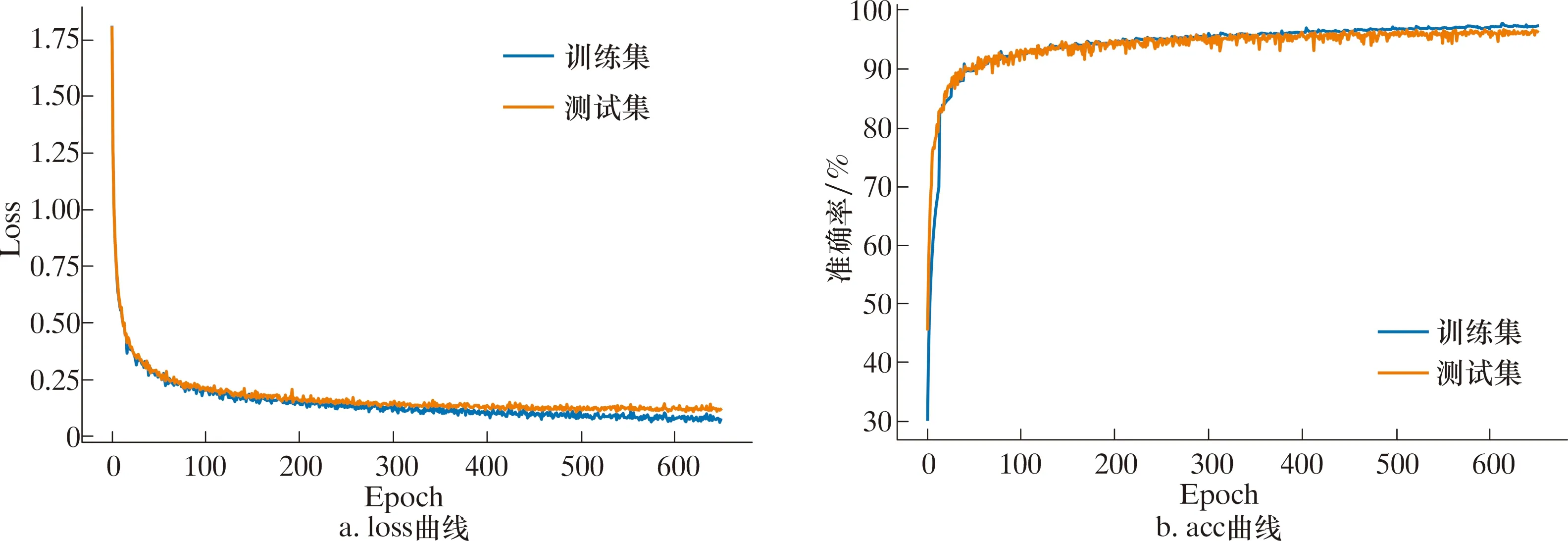
图8 CNN-BiLSTM模型训练过程Fig.8 Training process of CNN-BiLSTM model

3.4 不同输入对比

在第一个试验中，比较了以角速度、弯曲应变和角速度+弯曲应变作为输入的CNN-BiLSTM模型的性能。图9、图10分别是3种输入下CNN-BiLSTM网络测试集的混淆矩阵及评价指标。从图9和图10可以看出，当采用单一角速度输入时，整体分类效果较差，而采用角速度和弯曲应变双信号输入时，分类效果最好。原始的角速度信号包含大量的噪声，这对以角速度作为输入的模型分类准确率有很大的影响。弯曲应变通过经降噪处理后的姿态角和里程计算得到，在识别精度上对比角速度有很大提高。但降噪后的数据会丢失掉部分内检测在局部波动特征(如焊缝、部分凹陷管段)上的信号特征，以弯曲应变作为输入的模型在焊缝、凹陷和包含这2类特征的混合信号中其精度低于角速度+弯曲应变的输入模型。

图9 不同输入混淆矩阵对比Fig.9 Confusion matrix comparison of different inputs

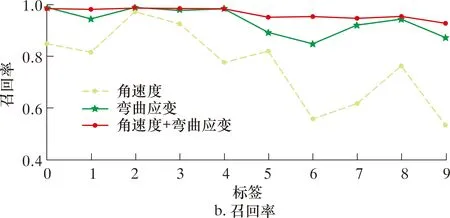
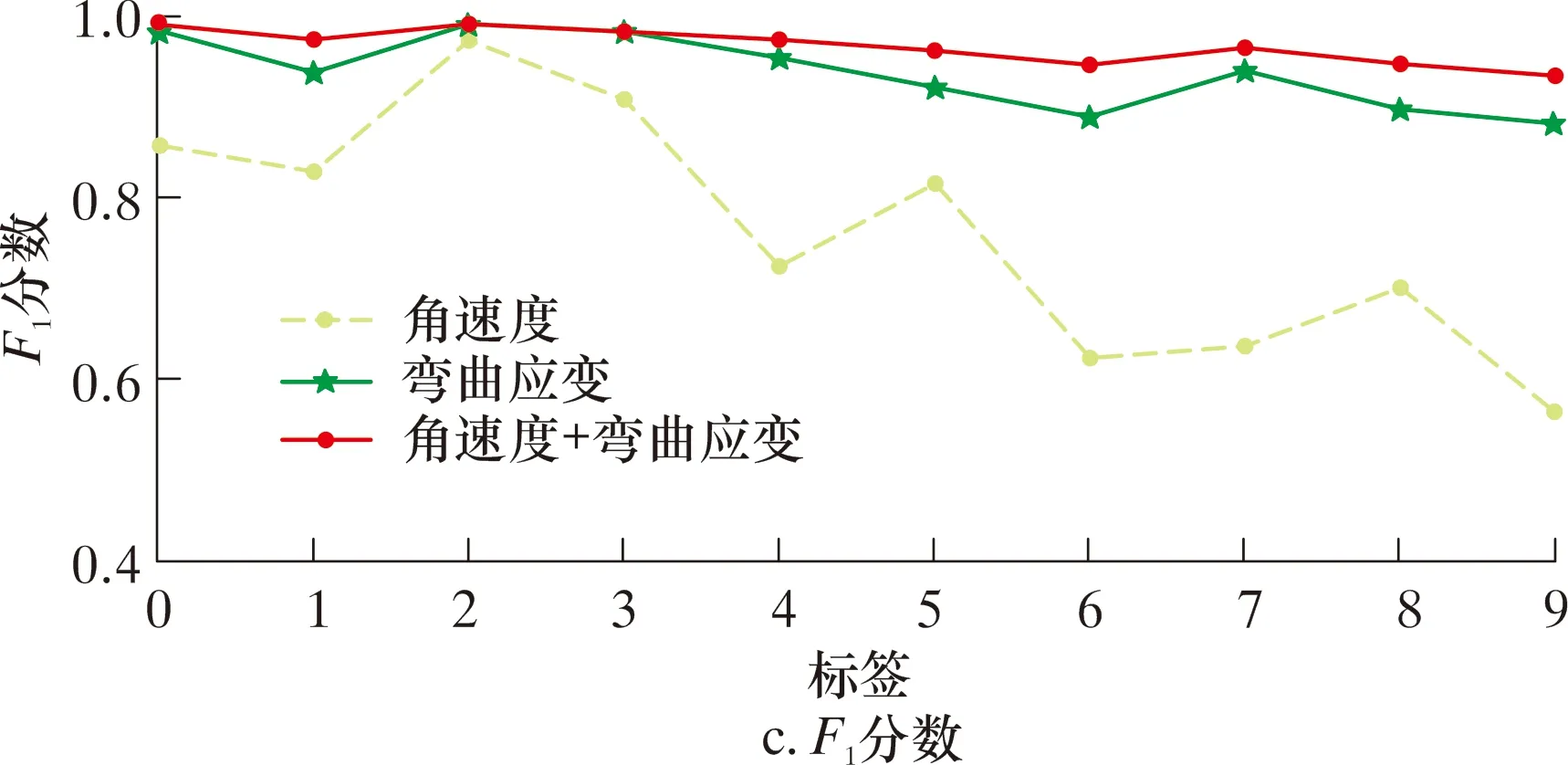
图10 不同输入CNN-BiLSTM网络性能Fig.10 CNN-BiLSTM network performance of different inputs

3.5 不同模型对比

图11为GRU(Gate Recurrent Unit，门拴循环单元)、CNN-RNN、CNN-GRU、LSTM、CNN-LSTM和CNN-BiLSTM这6种模型在测试集上的混淆矩阵。结果表明，采用CNN-BiLSTM的效果最好，准确率为96.90%，而采用CNN-RNN的效果最差，准确率为69.20%。从混淆矩阵中可知，CNN-BiLSTM模型对热弯的识别准确率最高，为98.70%，在冷弯、弯曲变形和凹陷方面的识别也有优异的表现。但其在直管+弯头和弯曲变形+焊缝2类中，准确率略低。热弯管段本身在IMU信号中与其他特征类型的区别更大，是该模型中最好的可分离信号；而直管+弯头管段主要出现在内检测器进、出弯头的时间过程中，其信号与弯曲变形管段相似，分类准确率较差。混合特征由于是2种不同的管段类型信号的组合，所以混合类型与本身的单独类型存在一些误差，整体的分类准确率要差于单独的管段类型。图12是6种不同模型在每个类别中的精度、召回率和F1评分方面的性能。

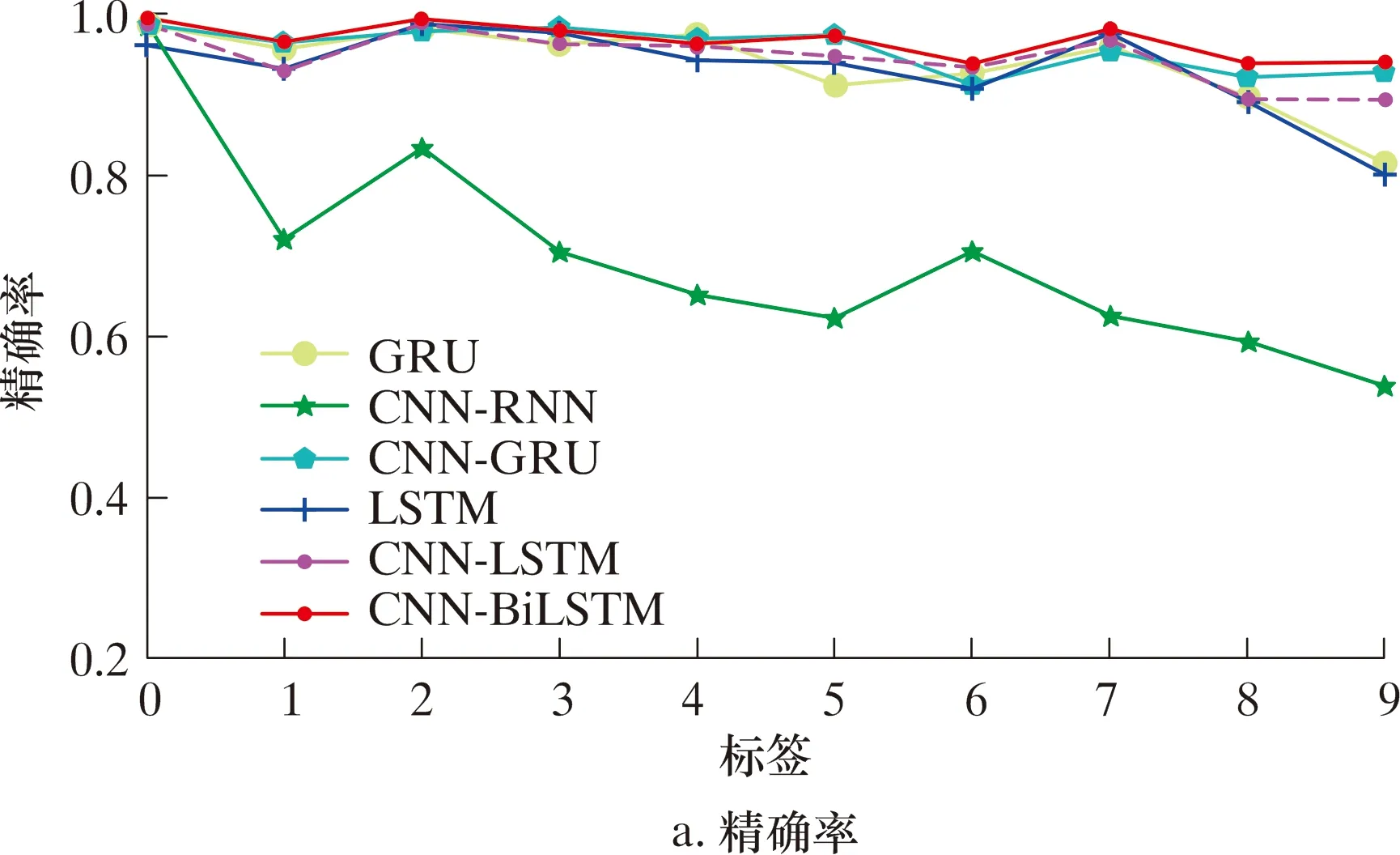
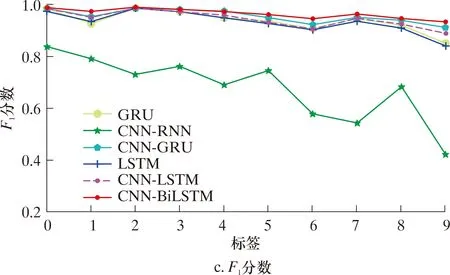
图12 不同网络模型性能Fig.12 Performance of different network models

由图12可知，CNN-BiLSTM模型的性能优于其他模型。

3.6 分类可视化

通过对比不同输入和模型，构建了基于CNN-BiLSTM网络和角速度、弯曲应变输入的管段类型分类模型。测试集训练前后的t分布随机邻近嵌入(t-Distvibufed stochastic Neighbor Enbedding，T-SNE)聚类可视化如图13所示。

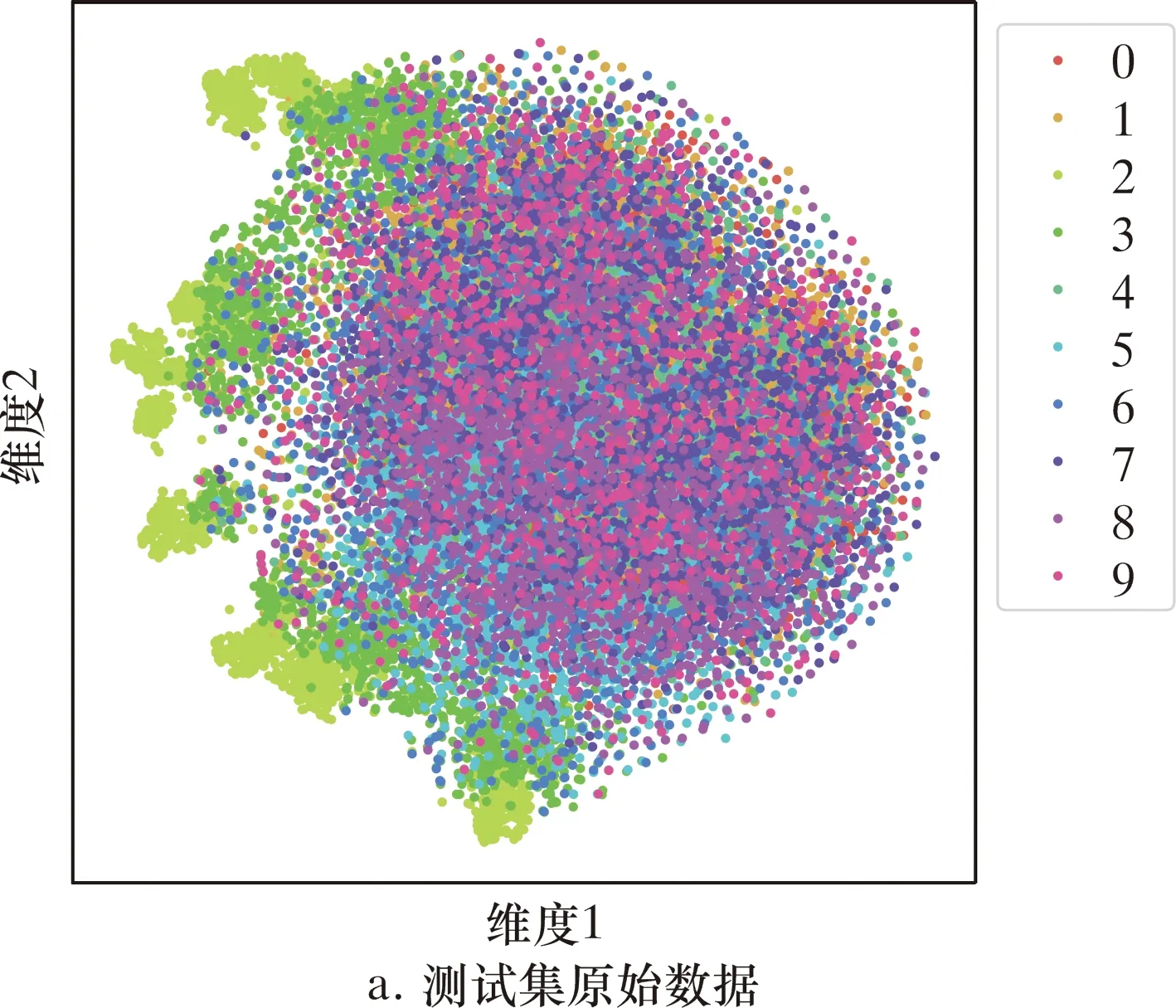
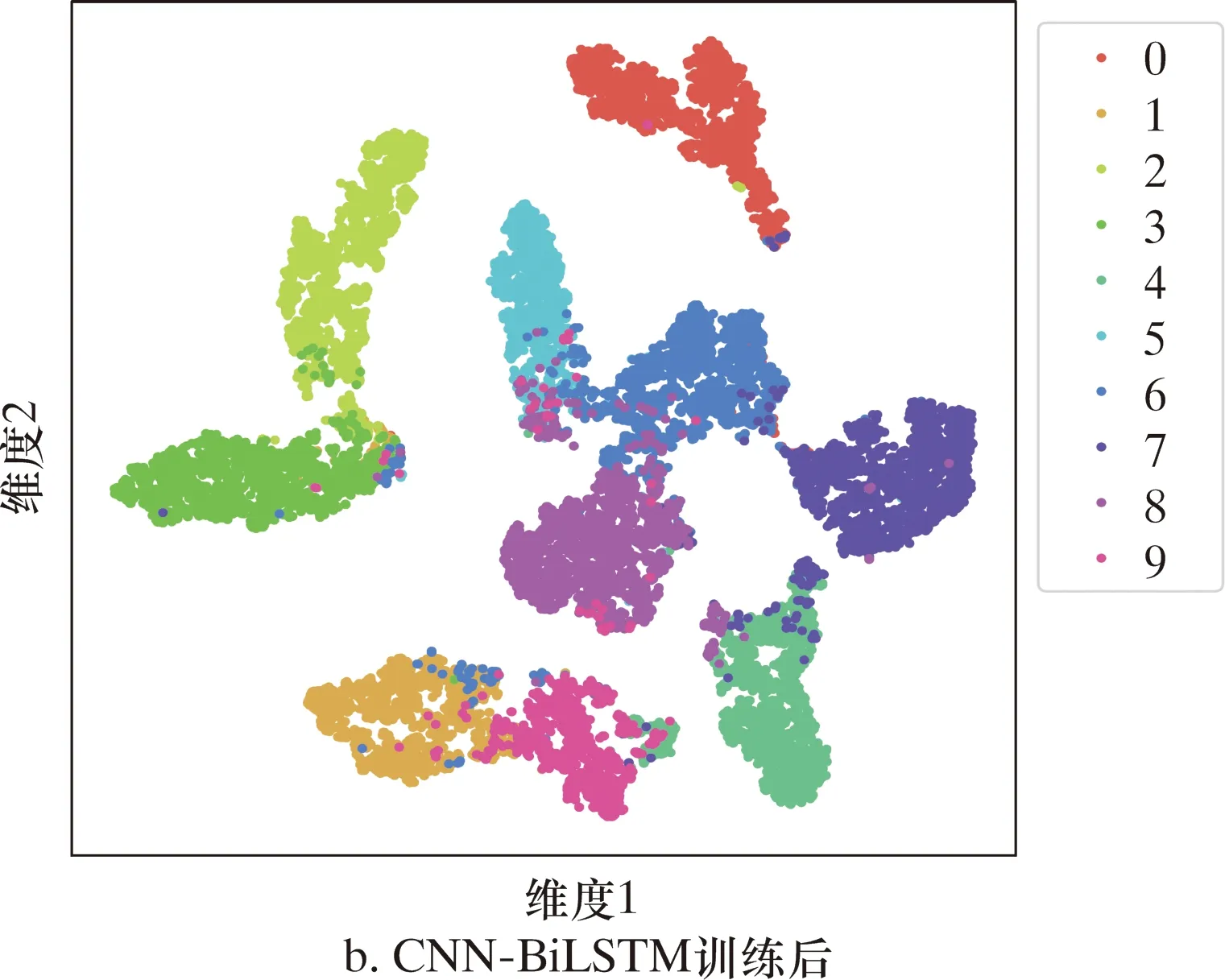
图13 10种管段类型分类可视化Fig.13 Classification visualization of 10 pipe section types

由图13可知，经过训练后的网络对于10种管段类型均具有较好的可分性。凹陷管段、弯曲变形管段、弯曲变形+焊缝管段是3类主要的管道变形缺陷，凹陷管段和弯曲变形管段分别是管道局部和整体的外力变形，而弯曲变形+焊缝管段容易在焊缝处造成应力集中。训练后的模型可以有效地将3类变形缺陷从10种管段类型中识别，识别的准确率分别为97.5%、97.4%、93.8%。