利用动态几何软件对大学生数学建模能力的影响分析研究

2023-12-01唐冶，李颖

黄山学院学报 2023年5期

唐冶，李颖

（1.安徽工程大学机械工程学院，安徽芜湖 241000；2.安徽工程大学艺术学院，安徽芜湖 241000）

0 引言

随着科学技术的进步，数字工具在大学教学中变得越来越重要，对数学建模[1]来说更是如此。现有文献普遍假设，建模活动中所使用的模型不但受学生数学知识与能力的影响，而且会被建模工具所影响[2]。因此，该方向的研究具有较大的现实价值。

目前已有一些研究成果，如章小童[3]提出了应该如何针对不同教育程度的学生使用信息化技术，以有效发展学生的建模能力的问题。但该问题迄今尚未得到令人满意的答案，解答该问题需要进行广泛的研究和理论分析。吴开琪[4]在基于现实问题的背景下，认为计算机和其他工具，有助于提升学生建模能力或构建适当的数学建模基础概念，其还指出，动态可视化在数字化教学背景下尤为重要。Blum 等人[5]分析了在建模周期中执行建模步骤所需的不同能力，并与例如简化、数学化、数学计算、解释和验证等子能力相对应。相关研究表明[6,7]，数字工具提供的可视化功能，会影响甚至可能会增强一般数学能力的开发。例如GeoGebra 等DGS 被认为有助于提高学生对建模背景的理解和建模能力的提高[8]。GeoGebra可以为建模时的各个过程提供支持，特别是其中的图形表示[9,10]。

迄今为止，很多问题尚无定论，例如在使用数字工具时，学生受教育程度的不同，会对其建模能力包括简化、数学化、解释或验证等子能力的有效获得产生怎样影响？为此，本文讨论了动态几何软件（Dynamic Geometry Software, DGS）的使用在开发学生建模能力中的促进作用。首先考虑数学工具在整个数学建模过程中的应用，讨论利用数字工具来描述建模过程的各种方式。然后，重点研究建模时的DGS 使用，并分析在利用DGS 执行数学建模时，学生可获得特定方面的能力提升。

1 研究的问题

为深度分析，本文将研究范围限制在数学化子能力的范围内，数学化是数学建模的子能力之一，因此DGS的使用可能会影响到相应过程的效果。

因此，本文的第一个研究问题为：当学生在利用DGS，或不使用DGS 进行数学建模的学习时，其数学化子能力的发展会不会存在差异？

另一个影响因素是学生对利用软件进行学习所持的态度。若学生不认可软件，其可能会拒绝进入深度学习状态。这引发了本文的第二个研究问题：程序相关的自我效能感（Self-Efficacy, SEF），与学生在使用GeoGebra进行学习时的态度，以及利用DGS 进行建模学习时的数学化子能力的开发是否存在关系？

2 提出的方法与实施过程

2.1 方案设计

SEF 的概念对应于自身完成某项任务的信心[11]。SEF被认为会对人们的行为产生很大影响。

为了回答上述问题，选取150 名大二学生进行对照研究。提供容量足够的计算机教学场地，在连续四节课中分析了利用数字工具进行教学，以及教师在教学单元中使用DGS 的不同情况。将30 个参与班级随机分配到一个DGS 组或一个纸笔组中。鉴于现实约束，本文研究中使用了便利样本（而非随机对照实验）。在每堂45 分钟的4 堂数学课过程中，学生成对地完成不同的开放式建模任务，任务难度不断增加且以空间几何内容为基础。向两个组提供相同的练习，区别在于：DGS 组被要求在进行4 项建模任务时使用DGS-GeoGebra，数字工具在建模过程中的使用如图1所示。DGS组和纸笔组接收几乎相同的学习任务。

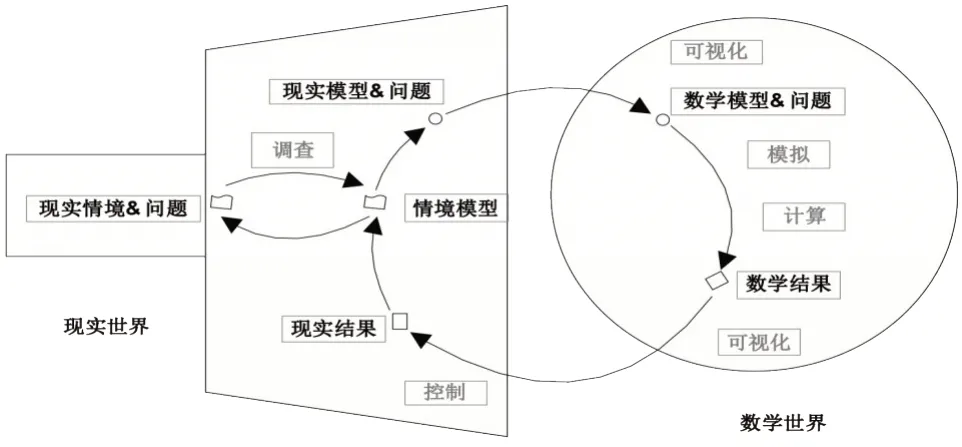
图1 数字工具在建模过程中的使用

实验中的开放式建模任务被设计为包含各种各样的解，重点在于检验学生在简化、数学化、解释和验证步骤中的能力。利用传统工具和DGS均可解决该任务。相对于分类方案，本文实验中采用所有任务均侧重于建模过程的所有步骤，且存在数据冗余和缺失情况，以接近现实问题。DGS-GeoGebra 的典型用途包括构建、绘制、测量，图2 给出了DGSGeoGebra 所有可能的使用方式。为确保学生能够掌握操作GeoGebra 的基本技能，DGS 组在教学单元开始时首先进行简短练习，其中还给出了软件的不同按钮功能的解释。学生可以通过该练习记住软件的重要功能。

图2 定性分析结果的方式

2.2 测试工具和调查问卷

下面简要描述测试工具的开发步骤。图3给出了对数学化子能力进行评估的测试项目样例。该任务基于“草捆任务”，向学生展示田间的草捆堆的真实情况。假设所有草捆均具有相同大小，并且是均匀和精确的圆形。此外，草捆的直径为1.50m，草捆向下一层陷入的深度为20cm。“数学化”指的是从简化的实际情况中建立数学模型的能力，因此学生的任务是将该情境转换为数学表示。

图3 草捆任务图例

为分析不同变量所造成的学生能力水平的变化，本文选择了加权似然估计法[12]（Weighted Likelihood Estimation, WLE），其通常被视为最精确的点估计法。如拟合指数（0.92≤WMNSQ≤1.07，t≤1.6）和图形模型测试所示，Rasch模型在数据上有着较好拟合。在对实验组之间的差异进行测试时，未发现项目功能上的显著差异。这表明本文实验中使用的测试工具能够较好地检测各组学生在能力上可能存在的差异。如研究问题2 所示，本文希望分析影响到DGS组中数学化能力发展的变量，例如学生运用程序相关的SEF。为测量程序相关SEF，要求DGS 组在第二个测量点完成一份调查问卷。对于数学化能力发展，程序相关的SEF 预计会比通用计算机SEF 产生更大影响，因此本文仅分析程序相关SEF的影响。

3 实验结果与分析

一般可以对DGS 处理的影响进行独立分析，而不受在预测试中已经存在的数学化能力的影响。所有测量点处的描述性数据如表1 所示，其中N表示参与者人数，M表示均值，SD表示标准偏差。

表1 数学化子能力的统计结果

回归模型中变量的相关性如表2 所示，其中，***p＜0.001；**p＜0.01；*p＜0.05。实验组结果中，DGS 的使用与不同测量点处的数学化能力之间没有显著相关性。3 个测量点的数据与媒介效应量相关。从第2 个点和第3 个点的测量值可知，协变量“实验组”均不是数学化能力的重要预测因子，也可以从表3 回归模型系数中看出这一点。在第3 个测量点处，实验组之间的差异不具显著性。这种情况下，DGS 组的预试估计值稍高。但需要谨慎对待这些结果，因为从第2 个测量点到第3 个测量点的数学课程是不受控的。