苯环线性六角链中任意两点间的电阻距离
2023-12-01赵舵舵朱子怡赵媛媛
赵舵舵,朱子怡,赵媛媛
(池州学院大数据与人工智能学院,安徽 池州 247000)
0 引 言
计算电网络图中任意两点之间的电阻距离问题一直备受关注[1-5]。Gervacio 教授研究了n部图中任意两点电阻距离,并得到了电阻距离的表达式[2]。晏卫根教授的团队在Gervacio教授研究基础上对环状电网络中的电阻距离进行了研究[3]。黄苏闽、李书超等得到了线性六边形(圆柱形)链的电阻距离和基尔霍夫指标公式,确定了线性六边形链中最大和最小的电阻距离[4]。Estradaf 教授基于相应拉普拉斯算子的光谱特性证明了新电阻距离和基尔霍夫指数的几个结果[5]。
在最近的二十年来,一些化学图的电阻距离成为了研究热点。Barrett教授等人研究了线性三边形链的电阻距离[6]。陈海燕教授得到了线性四边形链中任意两点电阻距离的表达式,并进一步地确定了其中最大和最小的电阻距离,分析电阻距离的单调性和渐近性质[7]。
苯是一类重要的化合物,其图结构往往用六边形表示,研究由苯环组成的六边形系统中任意两点的电阻距离有着重要意义。电阻距离可以描画分子之间的类液,也是波状的强力的通讯桥梁。一个苯链就是具有以下性质的一个苯系统[5]:1.它没有同时属于三个六角形的顶点;2.它没有多于两个的六角形相邻。如果一个苯链中不含有弯曲的地方,就称该苯链是直苯链,也就是我们本文研究的苯环线性六角链。运用电路缩减原理计算苯环线性六角链初始点间的任意两点电阻距离,通过等效电阻原则及电路缩减原理得出新增点与其他点间任意两点的电阻距离。
1 准备工作
首先介绍苯环线性六角链的空间结构,将其变形为普通的线性六角链,如图1所示。
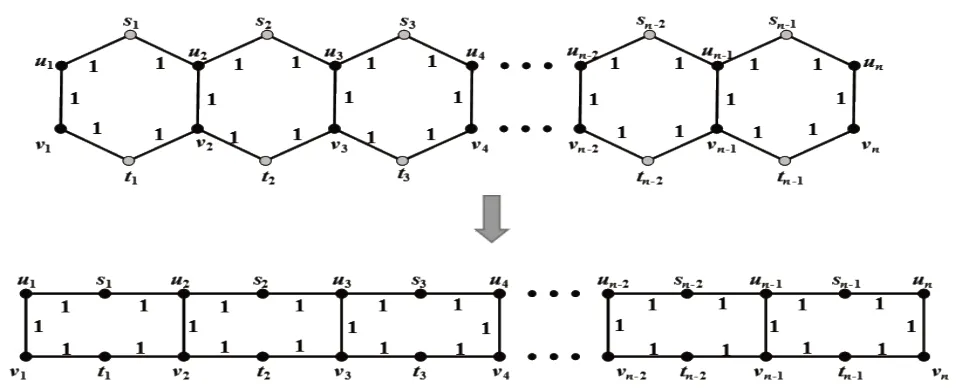
图1 苯环线性六角链变形
变换后的线性六角链可以通过线性四角链将按照一定的规则进行加点实现,如图2所示。
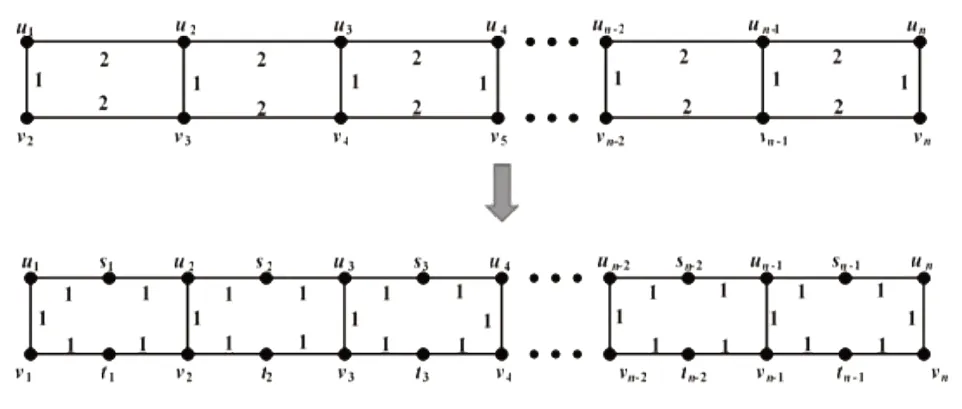
图2 线性四角链与线性六角链
由图2 可知,苯环线性六角链中的点可以分为两类,一类是原点,即{u1,u2,…,un} 与{v1,v2,…,vn} ;一类是新增点,即{s1,s2,…,s1} 与{t1,t2,…,tn} 。规定图G上的任意两点s,t间的电阻距离记为rG(s,t)。
给出电网络中的等效电阻和规则。
引理[8]:设N=(G,C)是一个电网络,对其任意的点i和j(i≠j),有
其中,C是一个电导函数,cik是边ik的电导。
定义以下3个函数:
2 主要结论
2.1 初始点间任意两点的电阻距离

图3 线性四角链

图4
根据上式,可以得到zn的解

图5
由图5,可以得到
综合上述公式,有
将公式进行运算,可以得到
并且,
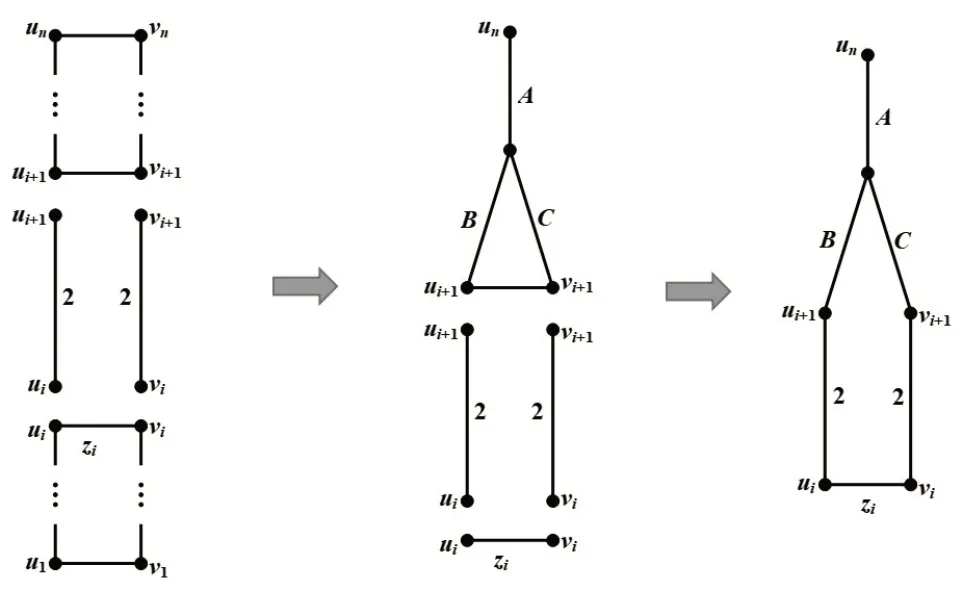
图6 关于顶点un,ui + 1及vi + 1做电路缩减
由公式(10)有
根据公式(11),我们可以得到
将公式(6)与(11)代入(12),能得到
可以验证,对于n≥i≥1,公式(13)也成立。
在上述结果的基础上,可以求解rWn(ui,uj),rWn(ui,vj)。对图关于顶点ui,vi及uj做电路缩减得到一个Y型图,如图7所示。
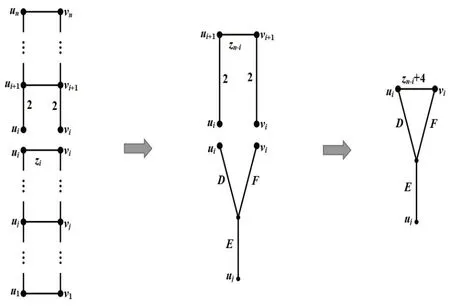
图7 关于顶点ui,vi及uj做电路缩减
根据图7,有
进而可得
和
联合公式(6)、(13)、(15)及(16)有
同理,可以验证对于n≥i≥j≥1,上述两个公式也成立。更进一步,有
2.2 新增点与其他点间任意两点的电阻距离
前文给定了原点之间任意两点的电阻距离,接下来将会求出新增点与其他点间任意两点的电阻距离。
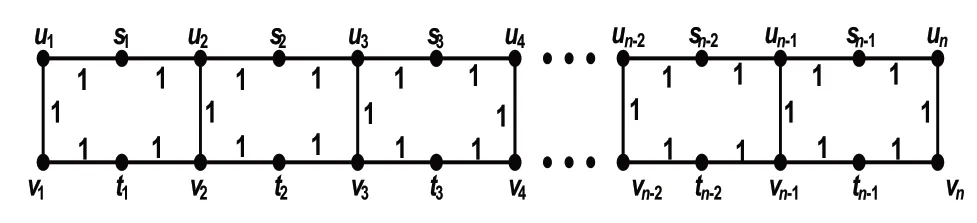
图8 线性六角链
将公式(19)乘以3减去(20),有
将公式(20)乘以3减去(19),有
联立公式,可以得到如下结果
对于任意i,j∈Z+,若i>j,则i≥j+ 1,对于,有
上式解得结果如下
联立公式有
由上式,可以得到
因而有
由于苯环线性六角链的结构及其对称性,可以验证,对于任意的n≥i≥j≥1,有
综上所述,可以得到下述定理:
定理1:对于苯环线性六角链,n≥i≥j≥1,其任意两点间的电阻距离如下:
1.初始点间任意两点电阻
2.新增点与其他点间任意两点电阻距离
由公式(17)和(18),可以发现,苯环线性六角链中新增点与其他点任意两点间的电阻距离可以由初始点的任意两点电阻距离来表示。
定理2:对于苯环线性六角链,n≥i≥j≥1,其任意两点间的电阻距离如下:
1.初始点间任意两点电阻
2.增点与其他点间任意两点电阻距离
