基于FIB MC 2010 的混凝土塑性损伤模型参数确定及实证分析

■张书文

（湖州交通规划设计院，湖州 313000）

混凝土塑性损伤模型（Concrete Damaged Plasticity，后简称“CDP 模型”）因能够同时考虑混凝土在受力过程中的塑性行为和损伤累积，在分析素混凝土或钢筋混凝土结构的非线性力学响应、评估结构的极限承载能力和预测结构破坏响应等方面得到广泛应用[1-3]。 准确选取和计算CDP 模型的参数对于描述混凝土在受力过程中的塑性变形、 强度退化、 损伤积累和裂缝扩展等非线性行为至关重要。目前针对CDP 模型从理论方面和应用角度的研究较多。 张骥[4]构造了一类适用于CDP 模型的新齐次屈服函数，显著提高了其分析精度。 李杰等[5]、吴建营等[6]采用拉伸和剪切损伤变量描述混凝土劣化表现，建立了基于断裂能的弹塑性损伤本构模型并解耦了损伤演化与塑性变形。 聂建国等[7]通过对比混凝土弥散开裂模型和CDP 模型，将2 种模型应用于钢筋混凝土构件的分析中以研究不同混凝土本构模型的适用情况。 张战廷等[8]、曾宇等[9]、杨飞等[10]按照规范[11-12]的建议确定CDP 模型中的相关分析参数，并通过算例对所计算的参数进行数值验证。 齐虎等[13]通过在ABAQUS 中二次开发进行了参数取值的系统研究，并利用数值模拟和振动台试验验证了其参数确定方法和本构模型的合理性。姜磊等[14]、Jin 等[15]利用将砂浆和ITZ（界面过渡区）确定为CDP模型，骨料确定为线弹性本构，对混凝土从细观力学角度进行受力分析。 综上所述，从理论方面修正CDP 模型使其更符合实际荷载作用条件下混凝土结构受力属于内部改进，目前已有相对成熟的研究结论。 应用ABAQUS 中内嵌的CDP 模型并通过相关规范（多为《混凝土结构设计规范》(GB 50010-2010)）确定其计算参数属于外部优化，然而与大量试验数据[16-17]对比，GB 50010 所给出的混凝土单轴抗拉、压强度标准值与试验结果相比较小，用于设计相对安全，用于损伤开裂研究相对保守。 而《FIB Model Code for Concrete Structures 2010》（后简称“FIB MC 2010”）中同标号混凝土给出的各项力学参数取值则相对较大。 基于此，本文根据FIB MC2010 所提供的混凝土塑性损伤本构模型及材料参数，计算确定ABAQUS 中CDP 模型参数，利用数值模拟方法分析无腹筋混凝土梁非线性力学特性，并通过文献[17]的试验结果对CDP 模型参数确定方法进行正确性验证。

1 ABAQUS 中CDP 模型

1.1 混凝土单轴拉伸行为和压缩行为

CDP 模型是一种基于塑性的、连续的混凝土损伤模型，其考虑混凝土破坏主要分为拉裂和压溃，屈服面（破坏面）演化由拉伸和压缩等效塑性应变（～εtpl和～εcpl）控制。 单轴拉伸和压缩损伤塑性特性描述如图1 所示。

图1 单轴拉伸和压缩损伤塑性特性描述

图1 对混凝土力学行为的描述虽然简单，但能抓住混凝土的主要变形特征。 单轴拉伸时，峰值拉应力σ0前应力应变关系为线弹性，材料不存在损伤；达到峰值拉应力σ0时，混凝土开始产生微裂纹；超过峰值拉应力σ0后，微裂纹成群出现，材料宏观表现出软化特性。单轴压缩时，屈服应力σc0前应力应变关系为线弹性，材料不存在损伤；屈服应力σc0至峰值压应力σcu为强化段， 这种现象是由于混凝土内部孔隙和微裂纹受到压缩时逐渐闭合所致；超过峰值压应力σcu后进入应变软化阶段。 若假定混凝土初始弹性模量为E0，则混凝土单轴拉伸和压缩工况下应力应变曲线可用下式描述：

式中：dt、dc分别为拉伸损伤变量和压缩损伤变量，其取值为0～1。 需要指出，损伤变量应避免超过0.99（即混凝土刚度值降低不超过99%）。

1.2 拉伸硬化与压缩行为定义

在ABAQUS 中，通过在混凝土受拉行为软化阶段引入“拉伸硬化（TENSION STIFFING）”以模拟混凝土开裂后钢筋的荷载传递作用（如：钢筋与混凝土的粘结滑移效应）。 定义拉伸硬化的方式有3 种，分别为后继破坏应力与开裂应变关系、后继破坏应力与开裂位移关系、直接输入断裂能Gf。 对于后继破坏应力与开裂应变关系，ABAQUS 按照式（3）将开裂应变（～etck=et-st/E0）转换为拉伸等效塑性应变，输入时要求计算所得拉伸等效塑性应变随开裂应变增加而增加。 需要指出，素混凝土或者少筋混凝土按后继破坏应力与开裂应变关系定义材料软化特性会导致分析结果存在网格敏感性，而后继破坏应力与开裂位移关系和直接输入断裂能的方法能够很好地解决网格敏感性问题。 在使用这两种方法时需要定义积分点的特征长度。 定义单元特征长度l0后，ABAQUS 按照式（4）将开裂位移转化为塑性位移。

ABAQUS 按照式（5）将非弹性应变（～ecin=ec-sc/E0）转换为压缩等效塑性应变，输入时要求计算所得压缩等效塑性应变随非弹性应变增加而增加。

1.3 单轴周期荷载下混凝土刚度恢复

ABAQUS 通过定义拉伸刚度恢复因子wt和压缩刚度恢复因子wc描述混凝土材料在单轴周期荷载作用下的刚度恢复行为，单轴周期荷载作用下混凝土的本构关系如图2 所示。 当荷载由拉伸→压缩，压缩刚度完全恢复，即wc=1；当压缩→拉伸，拉伸刚度无法恢复，即wt=0。

图2 单轴周期荷载作用下混凝土的本构关系

1.4 混凝土塑性

ABAQUS 通过流动势、屈服面（破坏面）及粘性参数（仅适用于Standard）等定义混凝土塑性。 流动势通过膨胀角j、偏心率e 定义；屈服面（破坏面）通过双轴受压极限强度与单轴受压极限强度之比sc0/sb0、不变应力比Kc等来定义；在保证计算精度的前提下，粘性参数取值越小，模型在软化阶段越容易收敛。

2 基于FIB MC 2010 的CDP 模型参数确定

2.1 FIB MC 2010 中混凝土参数

2.1.1 弹性模量与泊松比

根据FIB MC 2010，在无准确试验数据情况下，普通混凝土弹性模量可采用式（6）、（7）估算：

式中：E0为初始弹性模量（考虑初始塑性应变引起不可逆变形），MPa；Eci为初始割线模量，MPa；fck为混凝土抗压强度标准值，MPa；Df=8 MPa；Ec0=21500 MPa；aE与骨料岩性相关，玄武岩取1.2，石英岩取1.0，石灰岩取0.9，砂岩取0.8。

对于混凝土泊松比n，FIB MC 2010 建议其取值在0.14～0.26，一般而言取0.2 即可满足分析精度要求。

2.1.2 拉伸与压缩弹性极限点、断裂能

混凝土拉伸与压缩弹性极限点是混凝土弹性阶段和塑性阶段的分割点。 在CDP 模型中，以峰值拉应力σ0（即混凝土单轴抗拉强度平均值fctm）作为拉伸弹性极限点；以0.4 倍峰值压应力σcu（即混凝土单轴抗压强度平均值fcm）作为压缩弹性极限点（即屈服应力σc0=0.4σcu）；混凝土断裂能根据式（8）、（9）计算：

式中：GF为混凝土断裂能，N/mm； fcm为混凝土单轴抗压强度平均值，MPa。

2.1.3 单轴受压、受拉本构关系

（1）单轴受压应力应变关系。在FIB MC 2010 中，混凝土单轴受压应力应变关系如图3 所示，按式（10）～（12）计算：

图3 混凝土单轴受压应力应变关系（FIB MC 2010）

式中：εc1为峰值压应变；εc,lim为极限压应变；Ec1为割线模量，其值为峰值压应力与峰值压应变之比，MPa；k 为塑性参数。 εc1、εc,lim、Ec1、k 均可根据规范查表。

（2）单轴受拉本构关系。 在FIB MC 2010 中，混凝土单轴拉伸本构如图4 所示，开裂前的本构关系采用双折线应力—应变关系描述，如式（13）～（15）所示，开裂后本构关系采用双折线应力—开裂位移关系描述，见式（16）、（17）。

图4 混凝土单轴受拉本构关系（FIB MC 2010）

式中：w 为混凝土开裂位移，mm；w1=Gf/fctm，当σct=0.20fctm，wc=5Gf/fctm；当σct=0，拉应变为0.00015。

2.2 CDP 模型参数确定

2.2.1 弹性参数

由CDP 模型中混凝土单轴拉伸行为和压缩行为（图1）可知，混凝土在弹性工作阶段，仅存在1 个弹性模量值。 根据FIB MC 2010 可按式（6）计算弹性模量，聂建国[7]建议取压缩弹性极限点位置割线模量，需要指出，本文在分析时发现2 种方法计算所得弹性模量数值接近， 而后者概念更为明确，故弹性模量按压缩弹性极限点位置割线模量取值。 泊松比取0.2。

2.2.2 塑性参数

偏心率e 取0.1； 双轴受压极限强度与单轴受压极限强度之比sc0/sb0取1.16； 不变应力比Kc取0.667；膨胀角j 控制混凝土在较大非弹性压应变情况下的体积变化，取值范围为13°～56°；粘性参数取1×10-4。

2.2.3 压缩参数与拉伸参数

（1）压缩参数。 结合CDP 模型中混凝土单轴压缩行为、FIB MC 2010 单轴受压应力应变关系以及“2.2.1 弹性参数”中试算的弹性模量，即可得到混凝土压缩硬化关系（sc-ein）。 在计算混凝土压缩、拉伸损伤时，需要先计算混凝土损伤因子，而ABAQUS未提供混凝土损伤因子计算方式，本文依据Sidoroff能量等效原理计算混凝土压缩、拉伸损伤因子，具体如下：

FIB MC 2010 中混凝土拉伸软化阶段以应力—开裂位移关系给出，要通过式（19）计算拉伸损伤因子，需要将应力—开裂位移关系转化为应力—应变关系。 本文根据Bažant 提出的裂缝带理论，通过联立式（16）、式（17）、式（20）进行转变，进而求得混凝土拉伸损伤因子。 混凝土压缩损伤在求得压缩损伤因子后，联合非弹性应变即可求得。

（2）拉伸参数。 为避免模型分析时的网格敏感性，采用后继破坏应力与开裂位移关系或直接输入断裂能的方式描述混凝土拉伸硬化。 需要注意，对于CDP 模型在确定弹性模量和峰值拉应力后，即确定混凝土弹性阶段的应力应变关系。 混凝土拉伸损伤在求得拉伸损伤因子后，联合开裂位移即可求得。

2.2.4 压缩参数与拉伸参数

对于单调荷载作用下的混凝土损伤开裂数值模拟， 通常认为不发生裂缝张开后再闭合的现象。因此，CDP 模型中拉伸刚度恢复因子wt和压缩刚度恢复因子wc取默认值，即wt=0，wc=1。

3 实证分析：无腹筋混凝土梁试验

3.1 实例概况

本文以丁雅博[18]的“B-2.2-1.6”试件为例，基于CDP 模型建立有限元模型分析其损伤力学特性，并与试验所得荷载挠度曲线进行对比验证本文CDP模型参数确定的合理性。

“B-2.2-1.6”试件指剪跨比为2.2，配筋率为1.58%的混凝土无腹筋矩形梁，梁宽为200 mm，试件几何尺寸及配筋如图5 所示（图中a 为800 mm）。 试件所用混凝土的立方块抗压强度为42.15 MPa、 劈裂抗拉强度为3.16 MPa。 纵筋采用HRB400，直径为22 mm，其屈服强度为475.3 MPa， 极限强度为612.4 MPa，伸长率为26.83%，弹性模量按2.0×105MPa。

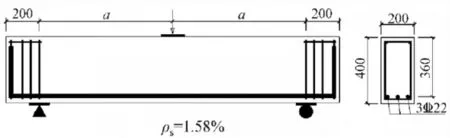
图5 “B-2.2-1.6”试件几何尺寸及配筋

3.2 有限元模型

利用大型通用有限元分析程序ABAQUS 建立“B-2.2-1.6”试件有限元模型，如图6 所示。 其中混凝土梁采用三维实体单元（C3D8R），垫块及加载块采用弹性刚体（C3D8R 单元）模拟，共计20 428 个。受拉钢筋以及构造钢筋均采用一维桁架单元（T2D2），共计719 个。 左侧垫块释放沿X 方向的扭转约束，其余5 个方向全部约束；右侧垫块除释放沿X 方向的扭转约束，还释放沿Z 方向的移动约束，其余4 个方向全部约束。 垫块与梁体、加载块与梁体之间采用绑定连接（Tie），钢筋与混凝土之间采用内置区域连接（Embed），暂不考虑的钢筋与混凝土之间的粘结—滑移作用。 模型按照位移方式进行模型加载，加载块处向下施加8 mm。“B-2.2-1.6”试件有限元模型中的需输入弹性及塑性参数如下：弹性模量E0为31 363.76 MPa、泊松比v 为0.2、膨胀角j 为35°、偏心率e 为0.1、sc0/sb0为1.16、不变应力比Kc为0.667、粘性参数为1×10-4，压缩行为及拉伸行为输入参数如表1 所示。

表1 “B-2.2-1.6”试件有限元模型压缩行为、拉伸行为

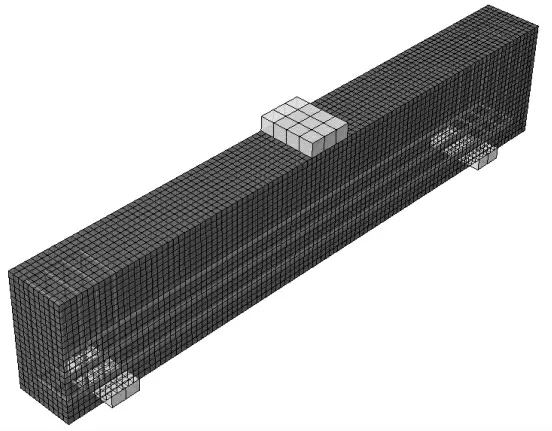
图6 “B-2.2-1.6”试件有限元模型

3.3 数值结果与试验对比

利用ABAQUS 对“B-2.2-1.6”试件进行损伤破坏分析，其损伤云图如图7（a）所示，图中损伤值较大的深灰色区域反映混凝土可能的开裂位置，黑色区域的混凝土不存在损伤。 由图可知，无腹筋钢筋混凝土梁破坏以斜裂缝和跨中位置的竖向裂缝为主。试验破坏照片见图7（b）。对比图7（a）和图7（b）可知，“B-2.2-1.6”试件的有限元分析结果（损伤位置）与破坏试验结果（裂缝分布）基本一致。

图7 “B-2.2-1.6”试件损伤云图与试验破坏图对比

同时，将有限元模型中支座反力（2 个支座合力）与加载块处竖向位移进行整合，得到“B-2.2-1.6”试件加载的力—位移关系，并将数值结果与试验荷载—挠度曲线进行对比，如图8 所示。 由图8 可知，“B-2.2-1.6” 试件有限元分析的极限承载力与试验所得的极限荷载基本一致，而加载过程中同位移（挠度）情况下，有限元分析结果比试验结果稍大，这是由于有限元模型中没有考虑混凝土初始缺陷，导致模型中的混凝土弹性模量高于试验所导致；而随着位移不断加载，模型损伤逐渐积累，直到与试验中“B-2.2-1.6”试件内部损伤相当时，有限元分析结果与试验结果基本接近。 从图中还可以看出，试验中未监测到试件破坏后荷载—挠度曲线下降段，而数值模拟过程可以得到下降段结果，这说明数值方法能合理预测钢筋混凝土结构破坏后承载能力。综上，根据FIB MC 2010 确定的CDP 模型参数可应用于无腹筋钢筋混凝土梁损伤破坏的预测分析。

图8 “B-2.2-1.6”试件力（荷载）—位移（挠度）曲线对比

4 结论

通过对ABAQUS 中CDP 模型特点以及FIB MC 2010 中混凝土单轴力学特性进行分析讨论以确定CDP 模型参数，并利用既有文献试验作为算例验证CDP 模型参数确定的合理性，得到以下结论：（1）根据FIB MC 2010 中混凝土单轴力学特性确定ABAQUS中CDP 模型参数可用于无腹筋钢筋混凝土结构损伤破坏的数值分析；（2）应用FIB MC 2010 确定的CDP模型参数，数值模型分析得到的极限承载能力与试验结果基本一致， 在不考虑模型初始损伤情况下，相同加载位移（挠度）数值结果比试验结果稍大。