自旋混合库珀对引起的Josephson 电流*

孟豪 吴修强

1) (陕西理工大学物理与电信工程学院,汉中 723001)

2) (盐城工学院物理系,盐城 224051)

通过求解Bogoliubov-de Gennes 方程研究一维S/FL-F-FR/S 结中Josephson 电流的输运特性,其中S 和F 分别是超导体和铁磁体,FL,R 是左右两侧具有非共线磁矩的界面层.研究发现,FL 和FR 界面能够产生自旋混合和自旋翻转效应,该效应能够将S 内一部分自旋单重对转化为F 内自旋相同的三重对.对于短S/FL-F-FR/S结,F 层内同时存在自旋单重对和自旋相同的三重对.于是,随着铁磁交换场和界面磁矩偏转角度差的增加,临界电流在一个基准面上振荡.若F 转变为半金属,则F 内仅剩自旋相同的三重对,临界电流的振荡特征消失.此外,FL 和FR 界面还能起到普通势垒的作用.这将导致临界电流随着铁磁厚度的增加展现出双重振荡行为,其中长波振荡源于铁磁体内自旋单重对的位相变化,短波振荡是由自旋单重对和自旋相同的三重对经过两个界面势垒时的共振隧穿效应引起的.

1 引言

随着自旋电子学的发展以及信息存储和数据传输量子器件的不断开发和利用,近年来人们对超导(S)/铁磁(F)异质结中超流的产生、输运和操控有极大的兴趣[1−8].根据Bardeen-Cooper-Schrieffer(BCS)理论可知,金属超导体内的Cooper(库珀)对是自旋单重对,它由自旋和动量都相反的两个电子组成.与此相反,铁磁体内的强交换相互作用会使电子自旋趋于同向.因此,超导与铁磁间的相互竞争会引起一系列有趣的现象.当前计算机的计算和硬盘读写过程仅仅利用了电子的电荷特性,为了提高计算速度和计算精度,人们很早就希望将电子的自旋自由度引入到量子计算和存储中.但是,单粒子自旋流在铁磁体内仅能传输几到十几纳米[9],这完全达不到实际应用的要求.令人兴奋的是,最近实验发现由自旋相同的三重对组成的自旋极化超流可以在强铁磁体和半金属(half-metal)中传播几百纳米[10,11],这为电子自旋在实际中的应用提供了一种有效的方法和途径.在过去的十年里,人们设计了一系列装置: 将超导体的零电阻特性与铁磁体中的自旋极化电流结合在一起,形成可以远距离传输的自旋极化超流.作为一个新的研究领域,它在自旋电子学和量子信息中表现出了非常诱人的应用前景.

超导体与均匀铁磁体接触可以在超导/铁磁界面附近形成邻近效应(proximity effect)[2]: 当Cooper 对从超导体穿透进入铁磁体时,铁磁体内的交换相互作用会使自旋单重Cooper 对(↑↓-↓↑)获得一个质心动量±Q(Q∝2h/(ℏvF),其中h为铁磁交换场,vF为费米速度),从而形成一种自旋单重对和自旋三重对的混合(↑↓)eiQR-(↓↑)e-iQR=(↑↓-↓↑)cos(QR)+i(↑↓+↓↑) sin(QR)[4,7],其中(↑↓+↓↑)表示自旋相反的短程自旋三重对.自旋单重对 (↑↓-↓↑) 在铁磁层内会随着质心坐标R振荡衰减,这种振荡行为可以引起一系列新颖的效应,如S/F 双层结构中电子态密度的空间振荡[12]以及超导转变温度Tc随铁磁厚度的非单调变化[13].若铁磁体具有非均匀磁矩,则有可能形成自旋相同的三重对.最具代表性的结构是在S/F 界面附近引入非共线磁矩,由非共线磁矩引起的自旋翻转(spin-flip)效应能够将S 内的自旋单重对(↑↓-↓↑)转化成F 内自旋相同的三重对 (↑↑) (或↓↓)[4,6,7].这种自旋三重对的波函数在空间上各向同性,具有空间坐标交换不变性和自旋交换不变性.因此,其波函数是空间坐标和自旋的偶函数.若要满足泡利不相容原理,该波函数必须是时间坐标的奇函数,这种新颖的配对方式称为奇频自旋三重对(odd frequency spin-triplet pair)[3].这种三重对不会被交换场破坏,能够在F 层内传输很长的距离,数量级可以达到自旋单重Cooper 对在正常金属内的穿透深度,因此被称为长程自旋三重对.

另外,两个超导体被一个铁磁体分开可以形成一个铁磁Josephson 结(S/F/S).这是一种非常有应用前景的自旋装置,其可以通过电子自旋来改变临界电流.前述的自旋单重Cooper 对波函数的振荡行为在均匀铁磁Josephson 结中表现为: 随着铁磁长度的变化Josephson 结的基态在0-态(相同的超导位相)和π-态(超导位相差为π)之间转变.这种0-π 态转变在实验中表现为临界电流随铁磁厚度和温度的增加振荡衰减[14−16].π-态Josephson 结已经在实际装置中被用于实现量子计算中的超导量子比特[17].

与之相比,若Josephson 结中的铁磁体具有非均匀的磁序结构,则铁磁体内形成的自旋相同的三重对 (↑↑) (或↓↓)能引起长程的Josephson 电流[18−22].很多实验已经观测到了上述自旋相同的三重对在铁磁体内的长程输运现象[10,23−28].在众多非均匀铁磁Josephson 结中,最著名的是Houzet 和Buzdin[21]提出的S/FL-F-FR/S 结构,其中FL和FR界面的磁矩方向与中间的F 层非共线.他们建议通过测量Josephson 结中的临界电流来证明自旋相同的三重对的存在.然而,他们的研究采用准经典模型求解Usadel 方程.这种准经典方法假定铁磁交换场远小于费米能h≪EF,并且需要满足严格的条件hτ≪1,其中τ 表示电子散射时间.由于铁磁体内多数电子和少数电子的输运性质差异较大,准经典方法失去了其有效性,这将导致一些奇妙的量子效应被忽略.另外,很多研究S/F 异质结的实验都采用强铁磁体,而准经典近似不能进行充分的定量描述.弥补准经典模型缺陷的一种有效方法是采用微观方法求解Bogoliubov-de Gennes (BdG)方程.对于非均匀铁磁Josephson 结,一般很难得出BdG方程的解析解,通常采用精确的数值计算对准经典结果进行修正.

基于上述原因,本文采用纯量子的Andreev(安德列夫)能谱法研究一维铁磁Josephson 结中的电流输运特性.研究发现,对于短的弱铁磁S/F/S 结,临界电流会随着铁磁厚度和交换场强度增加振荡衰减.与之相比,对于具有非共线界面磁矩的S/FL-F-FR/S 结,详细推导了自旋单重对和自旋三重对在FL-F-FR区域的变换和输运过程,得出FL和FR界面能够引起自旋混合(spin-mixing)和自旋翻转效应.这两个效应能够将S 层内的自旋单重对转化成F 层内自旋相同的三重对.于是,在短铁磁层内同时存在自旋单重对和自旋相同的三重对.因此,当铁磁交换场增加时自旋单重对位相的变化能够引起电流振荡,而自旋相同的三重对可以使电流维持在一个恒定的值.此外,随着铁磁厚度的增加,临界电流会显示出两种振荡行为的叠加,其中长波振荡源于自旋单重对位相的改变,短波振荡源于自旋单重对和自旋相同的三重对穿过FL和FR界面时产生的共振隧穿效应.

2 理论模型

如图1 所示,本文考虑一个一维S/FL-F-FR/S弱链接(weak link).F 层的自旋量子轴沿着z方向,Josephson 电流沿着y方向输运.取F 层厚度为d,系统的坐标原点位于F 层中心.BCS 平均场有效哈密顿量表示为[29]

图1 (a) S/FL-F-FR/S 结的结构示意图,其中F 内的粗箭头表示交换场方向,FL 和FR 为具有非共线磁矩的自旋活性界面;(b) Fj 界面处磁矩 ρj 的磁化方向,其中 j=L ,R分别对应左侧和右侧界面.θj和χj 分别表 示Fj 界面的极化角和方位角Fig.1.(a) Schematic diagram of the S/FL-F-FR/S junction,where thick arrow in F indicates the directions of the exchange field,and the FL and FR are spin-active interfaces with non-collinear magnetic moments;(b) the direction of magnetization ρj at the Fj interface,where j=L andR correspond to the left and right interfaces,respectively.θj and χj denote polar and azimuthal angles of the Fj interface,respectively.

超导能隙在超导电极中为恒定值,在铁磁区域不存在,可以写成如下形式:

其中Δ为能隙的幅值,ϕ为两侧超导电极的位相差.该近似在超导长度远大于铁磁长度时是合理的.F 层交换 场沿着z方向,可以表示为hz=h(-d/2＜y＜d/2),其中表示沿z方向的单位矢量.这里用一个δ函数ρ(x)=ρLδ(y+d/2)+ρRδ(y-d/2)模拟自旋活性(spin-active)界面,其中ρj(j=L ,R )为Fj界面处的磁化矢量.ρj的各分量通常可以用极化角θj和方位角χj表示为

其中ρj表示界面磁化强度.

下面分别对每个超导电极和铁磁层求解BdG 方程(4).对于超导能隙中一个给定的能量ϵ,可以得到左侧超导电极内的波函数:

利用上述边界条件可以建立16 个线性方程:

可得出两个Andreev 束缚态能量EAω(ω=1,2).下面考虑短Josephson 结情况,即F 层长度远小于超导相干长度ξS.在这种情况下,Josephson 电流主要源于Andreev 束缚态[30,31].在一维弱链接中Josephson 电流可由下面的通式计算:

其中Ω是与位相有关的热力学势.该热力学势源于激发谱,可以用下式计算[32,33]:

其中假定Δ,hz,Pj,θj和χj为处于平衡态的值.这些平衡值依赖于微观参数,能够使S/FL-F-FR/S结的自由能最小化[34].在(14)式中仅对所有正的Andreev 能量求和,即取 0＜EAω(ϕ)＜Δ.对于每个给定的ϕ值,数值求解(12)式得到两个自旋极化的Andreev 能级,然后根据(13)式和(14)式得出Josephson 电流.最终系统中的临界电流可以由Ic=maxϕ|I(ϕ)|导出.

在数值计算过程中,以超导能隙Δ作为单位能量,并取费米能EF=1000Δ.所有的长度和交换场强度分别以费米波矢kF的倒数和费米能EF为单位进行约化,电流以I0=2eΔ/ℏ 为单位进行约化.文中所有结果皆为温度T/Δ=0.1 时计算所得.需要说明是,在计算过程中铁磁体的厚度取值完全满足短Josephson 结的近 似条件(kFd≪1000).如图1 所示,规定Fj界面处的磁矢量ρj垂直于F 层磁矩,并在x-y平面内转动,于是θL=θR=π/2 .另外,规定左右两侧FL和FR界面的磁矩偏转角度差为 δχ=χR-χL.

3 结果与讨论

3.1 S/F/S 结中的Josephson 电流

图2 给出了不含左右界面层(PL=PR=0)时,Josephson 电流随F 层厚度d和交换场hz的变化特征.图2(a)显示了临界电流Ic变化的三维俯视图,可以看到电流幅值呈现黄蓝相间的条纹.这说明随着d和hz增加电流幅值周期性振荡.原本电流应该随着铁磁厚度和交换场的增加呈现正负振荡.正值对应 0 -态,电流方向为正.负值对应π-态,电流方向为负.但是一般在实验中仅测量电流的幅值变化,不考虑其方向变化.因此,对图2 中的电流都取了模值以便与实验对比.为了进一步说明该电流的振荡行为,在图2(b)中描绘了不同交换场下临界电流Ic随铁磁厚度d的变化特征.可以看到当F 层为正常金属(hz/EF=0)时电流缓慢衰减,无振荡出现.这是由于在正常金属中自旋向上和自旋向下的能带简并所致.当F 层为铁磁体时( 0＜hz/EF＜1),临界电流会随着厚度d的变化而显示出振荡行为,其振荡频率会随着hz的增加而增大.若将F 层厚度固定为kFd=60,则交换场取hz/EF=0.05,0.10,0.15 时电流 分别经 历0.5,1.0,1.5 个振荡周期.同样地,若固定铁磁厚度d连续改变铁磁交换场hz,临界电流也会展现出相同的振荡特征,见图2(c).

图2 S/F/S 结中Josephson 电流随铁磁特征的变化 (a)临界电流 Ic 随铁磁交换场 hz 和铁磁厚度d 的变化特征;(b)不同交换场下 Ic 随d 的变化特征;(c)不同铁磁厚度时 Ic随hz 的变化特征; hz/EF=0.15 时的(d)Andreev 能谱 EA(ϕ) 和(e)电流-位相关系 I(ϕ) .在所有图形中,界面极化强度取PL=PR=0Fig.2.Variation of Josephson current with ferromagnetic characteristics in the S/F/S junction: (a) Critical current Ic versus exchange field hz and ferromagnetic thickness d;(b) dependence of Ic on d for different exchange fields;(c) dependence of Ic onhz for different ferromagnetic thicknesses;(d) Andreev energy spectrum EA(ϕ) and (e) current-phase relation I(ϕ) forhz/EF=0.15 .In all panels,the strengths of interfacial polarization are taken as PL=PR=0 .

另外,为了说明Josephson 电流的0-π 态转变特征,图2(d)和图2(e)中分别给出了kFd=20.8,31.3 和41.6 时的Andreev 能谱EA(ϕ) 和电流-位相关系I(ϕ),这3 个特殊厚度分别对应图2(b)中的A,B和C三点.由于铁磁厚度较小,在超导能隙Δ内Andreev 能谱中只包含了两个能带.众所周知,Josephson 电流满足关系式I(ϕ)=Ic1sin(ϕ)+Ic2sin(2ϕ)+···[1].由于高阶电流的幅值非常小,一般情况下只考虑一阶电流Ic1和二阶电流Ic2的贡献.当铁磁厚度为kFd=20.8 时,两个Andreev能谱曲线几乎重合,此时Josephson 结处于π-态,即Josephson 电流近似地满足函数关系:I(ϕ)≈Ic1sin(ϕ+π) .当kFd=31.3 时,Josephson结 处于0-态和π-态转变的临界点,此时Andreev能谱分为上下两个能带.Josephson 电流的幅值减小,但其随ϕ的振荡频率翻倍.这是由于此时一阶电流完全消失(Ic1=0),系统中仅剩二阶电流,该电流满足关系I(ϕ)≈Ic2sin(2ϕ) .若kFd增加到41.6,Josephson 结处于0-态,则电流关系可以表示为I(ϕ)≈Ic1sin(ϕ).此时,两个Andreev 能带挨得非常近.这里值得注意的是,在以上kFd变化过程中Andreev 能谱曲线的形状会发生改变,但其始终关于ϕ/π=1 轴线对称,见图2(d).

3.2 S/FL-F-FR/S 结中的Josephson电流

首先讨论临界电流Ic随交换场强度hz的变化特征.图3 中当F 层为铁磁体时( 0＜hz/EF＜1),临界电流Ic的幅值会随着交换场hz增加而振荡.这种振荡不同于前述的0-π 态转变引起的振荡,电流幅值以Ic/I0～0.3 为基准面上下波动,最小幅值不能达到0.当F 层转变成半金属时(hz/EF≥1),振荡特征随之消失.另外,电流振荡的峰谷位置与界面磁矩偏转角度差 δχ有关.当F 层为铁磁体时,电流的振荡特征在 δχ=0 ,π 处最明显,在δχ=π/2 处最弱.电流在 δχ=0和δχ=π 处的振荡亦不相同.同一交换场下,若电流在 δχ=0 处为峰,则在 δχ=π 处必为谷,反之亦然.当F 层为半金属时,电流幅值会随着交换场hz的增加缓慢减小,但却不随角度差 δχ变化.

图3 临界电流 Ic 随铁磁交换场 hz和界面磁矩偏转角度差 δχ 的变化 特征 (a) kFd=25;(b) kFd=50;(c) kFd=70.在所有图形中,界面极化强度取PL=PR=1Fig.3.The critical current Ic versus exchange field hz and angle difference of interface magnetization rotation δχ : (a) kFd=25;(b) kFd=50;(c) kFd=70.In all panels,the strengths of interfacial polarization are taken as PL=PR=1 .

需要强调的是,上述临界电流在一个基准面上上下振荡是F 层内自旋相同的三重对 (↑↑)z,(↓↓)z和自旋单重对 (↑↓-↓↑)z共同作用的结果.自旋相同的三重对 (↑↑)z和(↓↓)z在F 层内的长程输运能够使临界电流维持在一个基准面上,并且随着F 层厚度d的增加基准电流的幅值几乎保持不变.另一方面,临界电流幅值的上下波动是由自旋单重对 (↑↓-↓↑)z穿过F 层时获得一个位相Qd引起的(Q∝2hz/ℏvF),或者说临界电流的振荡周期与Qd有关.若d取较小的值,要使临界电流振荡一个周期(Qd改变2π 角度),铁磁交换场hz必须增加较大的值,这样临界电流的振荡波长较大,而振荡频率较小.若d取较大的值,则振荡波长变小,振荡频率增大.在图3(a)—(c)中,分别给出了铁磁厚度kFd=25,50,75 时临界电流Ic随交换场hz的振荡特征,可以看出随着d的增加临界电流的振荡频率明显增大,这与上述物理解释完全一致.另外,图3 所示的临界电流基准值Ic/I0～ 0.3 并非一个普适常数.这是由于基准电流是由F 层内自旋相同的三重对 (↑↑)z和(↓↓)z的数量决定的,而自旋相同的三重对的数量取决于界面FL层和FR层的转化效率——界面FL层和FR层将超导体内的自旋单重对 (↑↓-↓↑) 转化成铁磁体内的自旋相同的三重对 (↑↑)z和(↓↓)z的转化效率.也就是说,临界电流的基准值会随着界面极化强度PL和PR变化.根据后面将要论述的临界电流随界面极化强度的变化规律可以粗略估算出临界电流基准值最大可以达到Imax/I0～0.4 .

下面详细论述自旋单重对和自旋三重对在S/FL-F-FR/S 结内的转化和输运过程,这样可以更好地解释上述电流的变化特征.在S 内的自旋单重对 (↑↓-↓↑) 在进入FL区域后受到界面交换场的作用而形成一种自旋单重对和三重对的混合(↑↓-↓↑)θ,χcos(QR)+i(↑↓+↓↑)θ,χsin(QR),其中下标 (θ,χ) 表示自旋单重对和三重对在 (θ,χ) 方向的投影.由于F 层沿着z方向极化,则从FL层到F 层的过程中铁磁体的极化方向将发生旋转.自旋单重对从FL层进入F 层具有旋转不变性[7,35]:

FL层内沿着 (θL,χL) 方向极化的自旋三重对在进入F 层后会进行如下变换[7,35]:

为了使临界电流达到最大,FL层和FR层的磁矩被限定在x-y平面内旋转,此时θL=θR=π/2 .于是,上述自旋三重对的变换公式可简化成:

以上自 旋三重对由 (↑↓+↓↑)θL,χL转变为 (↑↑)z和(↓↓)z的过程被称为自旋翻转效应.紧接着上面的过程,自旋三重对从F 层进入FR层将会经历如下变换[35]:

将θR=π/2 代入(18a)式和(18b)式,化简后再代入(17)式可以得到:

若忽略FR区域内自旋相同的三重对和对Josephson 电流的贡献,并取界面磁矩偏转角度差 δχ=χR-χL,则自旋三重对通过整个FL-F-FR区域的传输过程可以总结为

该传输过程说明自旋三重对通过整个铁磁区域后能够获得一个振幅因子 cos(δχ),这将导致临界电流的幅值随角度差 δχ改变.从以上结论可以看出,当F 层厚度较小时其内同时存在自旋单重对(↑↓-↓↑)z、自旋相同的三重对 (↑↑)z和(↓↓)z.其中自旋单重对能够引起一个短程的超流,该超流会随着铁磁交换场hz和厚度d的增加而振荡衰减.与之相比,自旋相同的三重对可以不受铁磁交换场的影响在F 层内远距离传输,从而引起一个长程的超流.这种长程超流随着hz和d的增加衰减得较为缓慢,且不会产生振荡效应.因此,在自旋单重对和自旋相同的三重对的共同作用下,临界电流会随着hz和d的增加在一个基准面上起伏振荡.另外,若固定F 层的厚度和交换场强度,临界电流会随着 δχ的改变而显示出振荡行为,并在 δχ=0,π 处幅值较大,在 δχ=π/2 ,3π/2 处幅值较小.以上结论与图3 中的数值计算结果相符.

需要特别指出的是,若F 层由铁磁体转变成半金属,则其费米面处仅有自旋向上的能带存在,因此只有自旋向上的三重对 (↑↑)z可以在F 层内传输,自旋向下的三重对 (↓↓)z被完全禁止.此时,在F 层内自旋单重对 (↑↓-↓↑)z也会被完全抑制,由其引起的振荡效应随之消失.此时自旋三重对在铁磁区域的输运过程可以描述如下:若忽略FR区域内的自旋相同的三重对和对Josephson 电流的贡献,则自旋三重对经过整个铁磁区域后能够获得一个位相因子 eiδχ,但不能得到振幅因子.因此,半金属Josephson 结中的电流满足关系式I(ϕ)≈-Icsin(ϕ+δχ),其中临界电流Ic的幅值不会随 δχ变化.

接下来讨论具有非共线磁矩的FL和FR界面引起的共振隧穿效应.如图4(a)和图4(b)所示,当F 层为弱铁磁体(hz/EF=0.1)时,随着厚度d的增加,临界电流Ic的幅值显示出两种振荡行为的叠加.第一种振荡的波长为kFλ1≈60,其波长较长称为长波振荡.第二种振荡的波长kFλ2≈3,该波长非常短,称为短波振荡.当交换场增大到hz/EF=0.5 时,长 波振荡的波长变为kFλ1≈12,而短波振荡的波长kFλ2保持不变,如图4(c)和图4(d)所示.若F 层转变为半金属(hz/EF=1.01),随着厚度d的增加临界电流的长波振荡消失,短波振荡虽未消失但其波动幅度变得非常微弱.此时,临界电流基本维持在Ic/I0～0.4 的基准面上.在半金属厚度固定的情况下,临界电流不再随角度差δχ变化,见图4(e)和图4(f).根据以上临界电流的变化特征,可以推断得出长波振荡是由自旋单重对穿过F 层后获得一个位相Qd引起的.如引言部分所述,临界电流以Qd为函数进行振荡.已知Q∝2hz/(ℏvF),若hz取较小的值,则Q亦较小,要使临界电流振荡一个周期(Qd改变 2π 角度),铁磁厚度d必须增加较大的值,此时长波振荡具有较大的波长.与之相反,若hz取较大的值,则长波振荡的波长变小.由此说明长波振荡的波长与铁磁交换场hz成反比.当F 层变为半金属时,自旋单重对被完全抑制,长波振荡随之消失.此时,F 层内仅存自旋相同的三重对 (↑↑)z,其在半金属内可以远距离传输.因此,临界电流随厚度d的增加衰减得非常缓慢,且短波振荡依然存在.

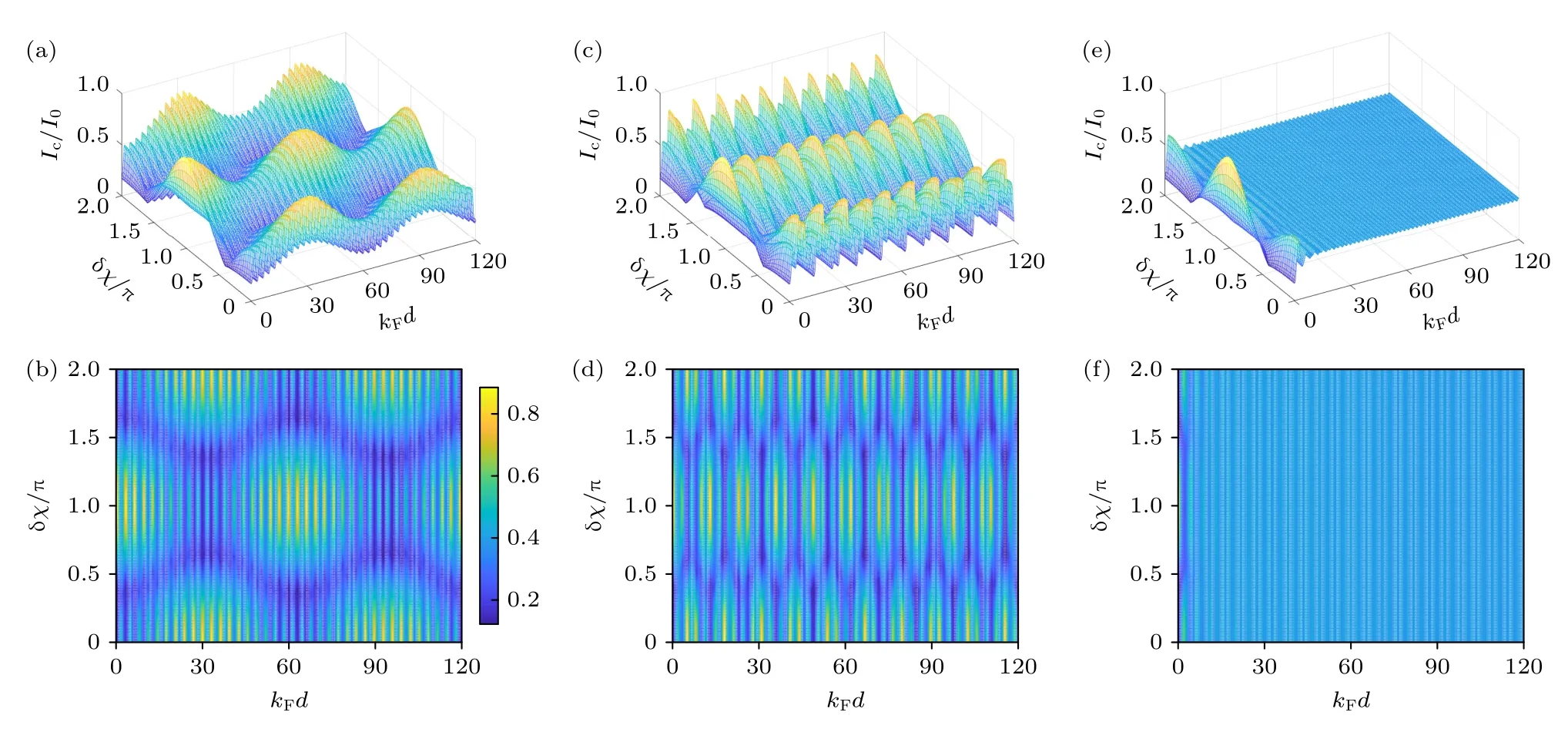
图4 临界电流 Ic 随铁磁层厚度d 和界面磁矩偏转角度差 δχ 的变化特征 (a),(c),(e) 电流变化的侧视图;(b),(d),(f) 电流变化的俯视图.(a),(b) hz/EF=0.1 ;(c),(d) hz/EF=0.5 ;(e),(f) hz/EF=1.01 .在所有图形中,界面极化强度取PL=PR=1Fig.4.Variation of the critical current with ferromagnetic thickness d and angle difference of interface magnetization rotation δχ :(a),(c),(e) Side view of current changes;(b),(d),(f) top view of current changes.(a),(b) hz/EF=0.1 ;(c),(d) hz/EF=0.5 ;(e),(f) hz/EF=1.01 .In all panels,the strengths of interfacial polarization are taken as PL=PR=1 .

为了进一步说明以上两种振荡的变化规律,图5(a)给出了 δχ取3 个特殊值时临界电流Ic随厚度d的变化.可以看到当 δχ=0 和π 时临界电流的幅值较大,长波振荡的波长为kFλ1≈60 .与之相对比,δχ=π/2 时临界电流的幅值减小,长波振荡的波长也减小为kFλ1≈30 .对比长波振荡的轮廓可以看出,当 δχ=0 时临界电流在kFd=30 附近为峰,而当 δχ=π 时此处的临界电流变为谷.为分析短波的振荡特征,图5(b)和图5(c)给出了3 个特殊铁 磁厚度kFd=29.9 ,31.5 ,33.0 的Andreev能谱和电流-位相关系,分别对应图5(a)中的A,B,C三点,其中A,C点为短 波振荡的峰值 点,B点为谷值点.可以发现,A,C两点的Andreev 能谱和电流-位相关系几乎完全重合.此时,能隙Δ内含有两条能带,并且呈对称结构,而Josephson电流近似满足关系式I(ϕ)≈Ic1sin(ϕ+π) .B点除了幅值有所减小外,电流-位相关系几乎保持不变.该特征说明短波振荡并不是由自旋单重对的位相变化引起的.另外,如图5(b)中的插图所示,当kFd=29.9和33.0 时临界电流随 δχ的变化特征几乎完全相同,即随着 δχ增加临界电流先减小,并在δχ=0.6π 处降到最小,然后在 0.6π＜δχ＜1.4π 区域处于一个平台,接着从 δχ=1.4π 处开始增加,并在 δχ=2π 处达到最大.当kFd=31.5 时,临界电流随 δχ的变化特征不同于以上两个厚度,而是在δχ=0.66π 处最小,在 δχ= π 处最大.由此可得出,当kFd=29.9 ,33.0 时,Ic随δχ同步变化; 而当kFd=31.5时则与之不同.最后,图5(d)和图5(e)给出了kFd=29.9,Andreev 能谱和电流-位相关系在不同角度差时的变化特征.可以看到,当 δχ=0,π/2,π 时Andreev 能谱都显示出关于ϕ/π=1 轴线的对称结构.这里需要强调的是当 δχ由0 增加到 π/2 时,一阶Josephson 电流完全消失,二阶电流随之显现,并满足关系式I(ϕ)≈Ic2sin(2ϕ) .当δχ增加到π 时,电流会获得一个额外的位相π,电流-位相关系变为I(ϕ)≈Ic1sin(ϕ) .

图5 (a) δχ 取3 个特殊 值时临界电流 Ic 随铁磁 层厚度d 的变化特征;(b),(c) δχ=0时的Andreev能谱 EA(ϕ) 和电流-位相关系 I(ϕ) (图(b)插图描述了 Ic随δχ 的变化);(d),(e) kFd=29.9 时的Andreev 能谱 EA(ϕ) 和电流-位相关系I (ϕ) .在所有图形中,其他参数为 hz/EF=0.1 和PL=PR=1Fig.5.(a) Variation of the critical current with ferromagnetic thickness d when δχ takes three special values;(b),(c) Andreev energy spectrum EA(ϕ) and current-phase relation I(ϕ) for δχ=0 (the inset in panel (b) illustrates the dependence of Ic on δχ);(d),(e) Andreev energy spectrum EA(ϕ) and current-phase relation I(ϕ) for kFd=29.9 .In all panels,other parameters are hz/EF=0.1 and PL=PR=1 .

根据以上计算结果,可以分析得出短波振荡是由自旋单重对和自旋相同的三重对的共振隧穿效应引起的.这是因为具有非共线磁矩的界面层除了能够将超导体内的自旋单重对转化为铁磁体内自旋相同的三重对外,还可以起到普通势垒的作用.根据量子力学的结论[36−38]可知,当粒子以低于势垒高度的能量E( 0＜E＜V0,V0为势垒高度)入射到含有双势垒的系统中时能够产生一个共振隧穿效应.该效应表现为: 粒子的透射系数或透射概率会随着两势垒间距的增大而展现出周期性的振荡峰,透射系数的最大值可以达到1[36].与之类似,超导体内的自旋单重对在穿过FL和FR界面层时也可以产生共振隧穿效应,即Josephson 电流的透射概率随着两界面层间距(即中间铁磁层厚度d)的增加而产生周期性的振荡峰.需要强调的是,这种周期性振荡峰的位置只与铁磁厚度d有关,不会受铁磁交换场hz的影响.当F 层转化为半金属时,F 层内仅存的自旋相同的三重对也能产生共振隧穿效应,但是由其引起的电流共振峰幅值却非常小.

最后,讨论临界电流Ic随界面极化强度PL和PR的变化规律.对于弱铁磁体(hz/EF=0.1),如图6(a)所示,当界面层不存在时(PL=PR=0)临界电流最大.随着极化强度的增加,临界电流先减小后增大,然后形成一个以PL=PR=0.92 为顶点的凸起.若继续增加极化强度,临界电流单调减小.对于中等强度的铁磁体(hz/EF=0.5),如图6(b)所示,临界电流虽然保持与前面相同的变化规律,但其顶点移至PL=PR=1.24,并且凸起的区域有所扩大.造成以上电流变化特征的原因可以解释如下.具有非共线磁矩的界面在Josephson 结中扮演了两个重要的角色: 1)在FL和FR界面处存在自旋混合和自旋翻转效应,该效应可将超导体内的自旋单重对转变为铁磁体内自旋相同的三重对;2)FL和FR界面还可以起到普通势垒的作用,即能够阻碍超导体内的自旋单重对向铁磁层的传播.因此,超导体内的自旋单重对在传输进入铁磁区域时有一部分会被界面层抑制,有一部分化成铁磁体内自旋相同的三重对.当界面极化强度PL和PR增加时,界面势垒对自旋单重对的抑制作用增强,这将导致电流幅值减小.与之相反,自旋相同的三重对的转化效率会随着PL和PR的增加而增大,于是自旋三重对对电流的贡献也随之增大.PL和PR刚开始增加时,前一种效应对电流的抑制作用大于后一种效应对电流的促进作用,最终导致电流幅值有所下降.当PL和PR增大到某个值时,后者对电流的贡献大于前者,电流幅值将会增大.自旋三重对的转化效率最高时,电流达到峰值.继续增加PL和PR的强度,自旋三重对的转化已经达到饱和,其对电流的贡献将不再增加,但界面势垒对电流的抑制作用会持续增加,此时电流幅值将会一直减小.

图6 δχ=0 时不同 铁磁交 换场下 临界电流Ic 随界面 极化强度PL和PR 的变化特征 (a) hz/EF =0.1;(b) hz/EF =0.5;(c) hz/EF =1.01.所有图形中,F层厚度取kFd=50Fig.6.Variation of the critical current with the strengths of interfacial polarization PL and PR for three different exchange fields in the case of δχ=0 : (a) hz/EF =0.1;(b) hz/EF =0.5;(c) hz/EF =1.01.In all panels,the thickness of the F layer is taken as kFd=50 .

此外,由图6(c)可以看到,当F 层转变为半金属(hz/EF=1.01)时临界电流的变化规律与前述的铁磁体情况不同.随着界面极化强度的增加临界电流先 增大后减小,在PL=PR=1 处达到最大.临界电流增加的速度较快,而减小的速度较为缓慢.这是由于在半金属中自旋单重对被完全禁止,其对电流不会作出任何贡献.因此,当左右两侧的界面层其中一个或同时不存在时,超导体内的自旋单重对无法转化成半金属中自旋相同的三重对,从而导致系统中不能形成Josephson 电流.随着PL和PR的增加,界面层的转化率将会提高,电流随之增大.当界面层的转化率饱和时电流达到最大.随后,若继续增加PL和PR,界面层的抑制作用会使电流减小.需要强调的是,与我们以前的工作相比[39,40],当前的结果中并未显示出临界电流随PL和PR的振荡效应.这是因为这里将FL和FR界面层简化成了自旋活性势垒,其厚度被忽略.通过数值计算证明,若用具有非共线磁矩的实际铁磁层代替界面势垒,则临界电流的振荡特性将会复现.

4 结论

本文采用纯量子的Andreev 能谱法,通过数值求解BdG 方程研究了一维S/FL-F-FR/S 结中Josephson 电流的输运特性.研究发现,若FL和FR界面不存在,隧穿进入F 层的自旋单重对会获得一个额外的位相Qd,该位相导致临界电流随着F 层的厚度和交换场强度增加而振荡衰减.若FL和FR界面存在,则非共线的界面磁矩可以扮演两个重要的角色.首先,FL和FR界面可以引起自旋混合和自转翻转效应,该效应可以将超导体内的自旋单重对转化为F 层内自旋相同的三重对.对于短S/FL-F-FR/S 结,F 层内同时存在自旋单重对和自旋相同的三重对.因此,随着F 层交换场的增加临界电流的幅值会在一个基准面上波动.若将铁磁体替换成半金属,F 层内的自旋单重对被完全禁止,电流的振荡行为随之消失.其次,FL和FR界面还能起到普通势垒的作用.随着F 层厚度的增加,临界电流幅值展现出长波振荡和短波振荡的叠加行为,其中长波振荡是由自旋单重对所得的位相Qd引起的,而短波振荡是由自旋单重对和自旋相同的三重对经过两个界面势垒时产生的共振隧穿效应引起的.以上研究结果为研制超导量子相干器件提供了理论依据,能够促进超导自旋电子学的发展.