光场辐照下稀磁半导体/半导体超晶格中自旋电子输运特性研究*

李春雷 郑军 王小明 徐燕

1) (首都师范大学初等教育学院,北京 100048)

2) (渤海大学物理科学与技术学院,锦州 121013)

3) (中国地质大学附属中学,北京 100083)

基于单电子有效质量近似理论和传递矩阵方法,理论研究了稀磁半导体/半导体超晶格结构中电子的自旋极化输运特性.主要讨论了光场和磁场联合调制对自旋极化输运的影响,以及不同自旋电子在该超晶格结构中的隧穿时间.理论和数值计算结果表明,由于导带电子与掺杂Mn 离子之间的sp-d 电子相互作用引起巨塞曼劈裂,因此在磁场调制下,不同自旋电子在该结构中感受到的势函数不同而呈现出自旋过滤效应,不同自旋电子的共振透射能带的位置和宽度可以通过磁场进行调制.同时在该结构中考虑光场时,自旋依赖的透射谱会因为吸收和发射光子而呈现出对光场的强度和频率响应;最后,通过不同自旋电子的高斯波包在该结构中随时间的演化给出了不同自旋电子的隧穿时间.本文研究结果对研究和设计基于稀磁半导体/半导体超晶格结构的高速量子器件具有一定的指导意义.

1 引言

源于自旋电子学的快速发展和自旋输运现象的潜在应用,各种微纳结构中电子自旋极化输运相关研究人们关注的越来越多.科学家们发展出了多种调控微纳结构中电子输运特性的手段,这些手段主要包括电调制、磁调制和光调制[1–8].对于微纳结构中的电子输运特性的研究,选取合适的半导体结构非常重要,基于ZnSe 或CdTe 的II-VI 族半导体量子结构被认为是非常优越的候选结构而被广泛关注.研究表明在包含稀磁半导体层的ZnSe/Zn1-xMnxSe 异质结中,有很多新奇的现象产生[9–13].当存在外加磁场,不同自旋方向的电子所感受到的势能大小不同,具体表现: 在稀磁半导体层中,自旋向上电子感受到的是一个势垒层,但是自旋向下的电子感受到的却是一个势阱层.产生这种独特特性主要源于sp-d 交换相互作用,即磁性掺杂原子与非磁性半导体结合导致局域不成对电子自旋与电子-空穴耦合作用.Egues[2]于1998 年通过在ZnSe/Zn1-xMnxSe异质结结构中调节外加磁场,理论研究了其中自旋输运特性,揭示了这一结构中不同自旋方向电子的极化输运现象,研究结果为实现自旋过滤光电器件提供了一种可能方案.随后,Slobodskyy 等[4]在II-VI 族半导体异质结构( ZnSe/Zn1-xBexSe/Zn1-xMnxSe) 中实验研究了其中的电流-电压特点,迈出了压控自旋过滤器的第一步.此后,科学家从理论[14,15]和实验[16–18]方面对稀磁半导体结构进行了广泛研究.Zhai 等[7,8,19–21]在该领域进行了系列研究,重点包括稀磁半导体/非磁垒,半导体/稀磁半导体等异质结构中自旋输运特性.如今,相关结构的研究主要集中在磁阻效应、能带弯曲效应、光致发光以及零场自旋极化等方面.目前,稀磁半导体/半导体结构可以实现调节外部参数进而控制半导体层内载流子的行为,这些特性使该结构有望被应用于磁控和光控超晶格器件.此外,通过调整光场的强度及频率,可以实现对低维结构中电子自旋输运的调控[22,23].调控的机制源于电子隧穿低维结构时吸收和发射光子与光场相互作用.20 世纪60 年代,研究人员首次在超导体/绝缘体/超导体结构中观测到光子辅助电子隧穿现象[24,25],自此光子辅助隧穿从理论[26,27]和实验[28,29]方面都得到了广泛的研究.

本文理论研究了稀磁半导体/半导体组成的超晶格结构中电子自旋输运特性,重点研究了磁场和光场对其中电子自旋输运的影响,同时计算了不同自旋电子隧穿通过该超晶格结构的时间.结果发现,磁场和光场的联合调制对不同自旋方向的电子在该结构中的隧穿影响有根本的区别,这些区别主要体现在隧穿时间和自旋极化方面.

2 理论模型

图1 给出了稀磁半导体/半导体超晶格势( ZnSe/Zn1-xMnxSe),其中图1(a),(b) 分别是B为2 T 和5 T 时,自旋向上和自旋向下电子对应的超晶格结构.此外还考虑了光场对隧穿的影响,因此在超晶格所在的区域考虑附加光场为V1cos(ωt),其中V1和ω 分别表示光场的强度与光子频率.这里忽略了电子的各种散射因素,且认为超晶格的生长方向(z方向)受限比垂直生长方向(x-y方向)受限强得多,因此电子在z方向的运动可以与x-y方向的运动解耦.这种情况下,x-y平面内电子的能级量子化为朗道能级En=(n+1/2)ℏωc,其中n=0,1,2,···,ωc=eB/m*,m*是电子 的有效质量,B是加在超晶格上的均匀磁场的磁感强度.这里选择朗道规范,磁矢势A=(0,Bx,0) .在有效质量近似下,该超晶格结构中z方向单电子的哈密顿量表示为

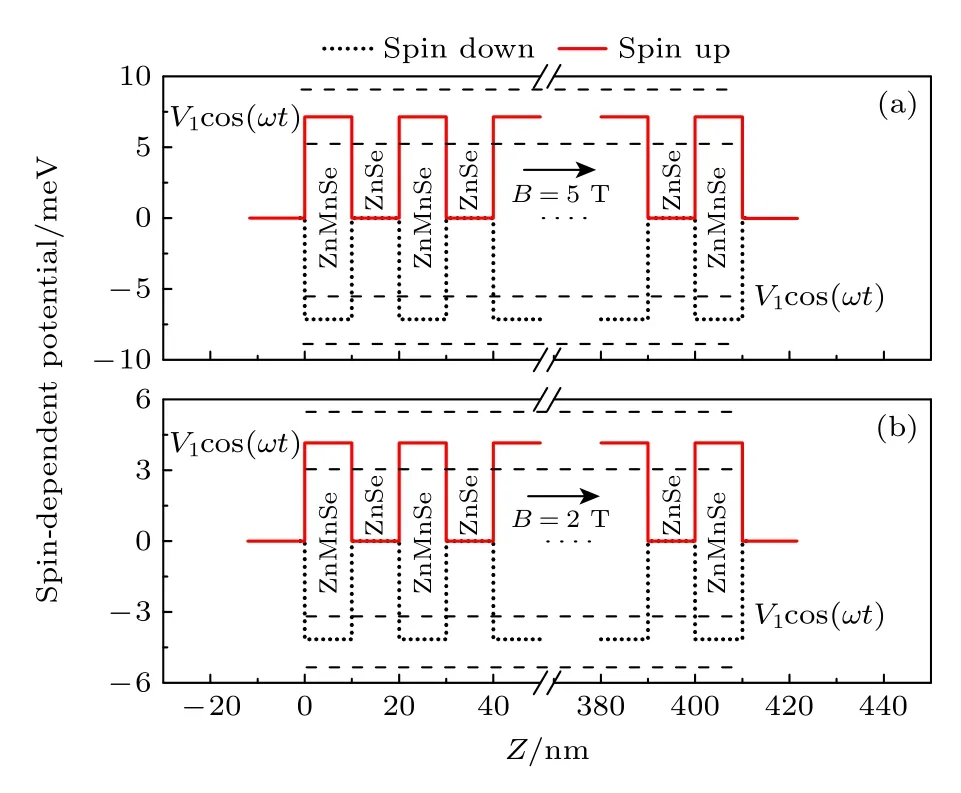
图1 光场 V1cos(ωt) 辐照下自旋相关ZnSe/Zn1-xMnxSe超晶格势(a) B=5 T;(b) B=2 TFig.1.Spin-dependent potential profiles of the ZnSe/Zn1-xMnxSe superlattice under a light field V1cos(ωt) :(a) B=5 T;(b) B=2 T.

其中,V(z) 是零磁场时 Zn1-xMnxSe/ZnSe 超晶格结构的导带带阶,Vσz是Zn1-xMnxSe/ZnSe 超晶格结构磁控自旋相关势.这个自旋相关势由稀磁半导体层在磁场下的巨塞曼劈裂引起,这个劈裂源于导带电子与Mn 离子3d 电子间相互交换作用.应用平均场近似,自旋相关势可以表示为Vςz=-N0ασzxeff〈Sz〉[2],其中N0α是sp-d 相互交换作用常数,σz=±12 是沿磁场方向电子自旋分量.xeff=x(1-x)12是Mn 掺杂有 效浓度,x是实际Mn 掺杂浓度.〈Sz〉是沿磁场方向Mn2+自旋分量的热平均值,这个热平均值可以通过修正的5/2 Brillouin 函数来计算,即其中Teff=T+T0是表示Mn-Mn 相互作用的有效温度,T是温度,T0取固定值1.7 K[30](取值与Mn 掺杂浓度有关,文中x=0.05).基于上文哈密顿量,求解对应的薛定谔方程,自旋相关波函数可表示为[23](假设超晶格结构在0—L之间)

这里,Jn-m(V1/ℏω) 是第一类贝塞 尔函数.n,m是引入光场引起准束缚边带指数.应用转移矩阵方法,可以计算出不同自旋方向电子在该稀磁半导体/半导体超晶格结构中电子的透射系数:

从中可以看出,透射系数T与(Ez,B,V1,ω) 都有依赖关系,具体情况将在随后的数值计算中给出.

最后,应用Gaussian 波包讨论电子在该结构中的隧穿时间,建构的时间相关波函数[31]为

其中取ϕ(k)=exp[-(k-k0)2/2Δk2] Gaussian 波包进行计算.在K空间,波包中心位于k0,Δk是波包的K空间宽度.

3 计算结果及讨论

在进行数值计算中,使用的参数如下: 稀磁半导体和半导体层电子的有效质量相等,同为m*=0.16m0(m0是自由 电子质 量).稀磁半 导体层Mn浓度x=0.05 ,相互交换作用常数N0α=0.26 eV,温度T=4.2 K,T0=1.7 K.图1 给出了 自旋相关稀磁半导体/半导体超晶格势,超晶格的周期分布为 (AB)NA(BA)N,其中A 代表稀磁半导体层,B 代表半导体层,数值计算中N取10,并且势垒层和势阱层宽度均等于10 nm,靠近发射极和集电极都是稀磁半导体层.图中红实线对应自旋向上电子态,黑点线对应自旋向下电子态,图1(a),(b)分别对应磁场B=5 T和B= 2 T 的情况.图中光场V1cos(ωt) 只考虑加载在超晶格范围( 0—410 nm),发射极和集电极没有光场辐照.

图2 给出了电子自旋相关透射系数和自旋极化度随电子入射能量的数值计算结果,为了便于对比,图中的透射系数变化曲线纵坐标依次进行了量值“0,1,2,3”的提升,自旋极化度曲线纵坐标依次进行了量值“0,2,4,6”的提升.数值计算中光子的能量为 ℏω=0.2 meV,光场强度分别取V1=0,0.2,0.4,0.6 meV,其中V1=0 对应无光场情况.左侧和右侧分别对应磁感强度B=2 T 和5 T 的情形.

图2 光场辐照下,不同磁 场强度 电子自 旋相关 透射系 数和自 旋极化 度,其中光 子能量 ℏω=0.2 meV,光场强 度V1=0,0.2,0.4,0.6meVFig.2.Spin-dependent transmission coefficients and spin polarization for different magnetic induction intensity under the light field,where the energy of photon is ℏω=0.2 meV,and amplitude of the light field is V1=0,0.2,0.4,0.6 meV.

图2 表明,在不考虑光场辐照时 (V1=0),透射谱构造出共振能带,这些共振能带被非共振带隙分开.自旋相关透射现象非常明显,自旋向上电子和自旋向下电子的共振带位置和宽度有明显区别,这种区别在磁感应强度大时表现得更为明显,主要根源于磁感应强度大时,不同自旋电子态感受到的势能区别更大的缘故.这也可以从图1 看出,对于自旋向上的电子,在B=2 T 时,感受到的势垒高度为V+=4.158 meV;在B=5 T 时,感 受到的势垒高度为V+=7.148 meV,因此,可以实现磁场对电子自旋透射的调控.考虑光场辐照时,上述共振能带会随着光场强度的增大而出现变形,变形主要表现在共振能带边缘不再是完全透射(透射系数为“1”的透射),同时伴随共振带展宽.其中变化比较显著的是在B=5 T时自旋向下的电子透射谱,在不加光场时,低能区透射系数几乎为零,但是随着光照强度增强,低能区透射系数明显增大,在特殊能量值时透射系数甚至达0.75,即出现了准束缚能带.这些特征源于电子在隧穿经过光辐照下的超晶格结构时与光场发生了能量交换,比如低能区域的电子可以通过吸收光子进入共振能带从而完成完全透射,这样在低能区形成准束缚能带,同样对于高能区域电子可以通过发射光子进入共振能带完成透射,这样在高能区也会形成准束缚能带,从透射系数图示中表现为出现新的透射谱.通过上面分析可以看出,共振能带的位置和宽度可以通过磁场和光场进行联合调控,这些性质对磁场与光场联合调控微纳量子结构在自旋过滤器件方面的应用有一定的指导意义.

下面讨论该超晶格结构中时间相关波函数随时间的变化关系,相关数值计算结果如图3 所示(计算没有考虑光场辐照,且当t=0 fs 时,波包中心位于z=0 处).其中图3(a),(b)分别是自旋向上和自旋向下电子的概率密度随时间变化情况.计算过程选用的参数: 磁感强度B=2 T,中心波矢k0=1.58×108m-1,波包的K空间宽度Δk=0.7×108m-1.从图3 可以看到,波包遇到超晶格势后分为两部分,一部分反射回入射空间,一部分透射进入超晶格结构中.其中反射波包基本保持一个主峰的波形,但是透射进入超晶格结构中的波包分裂为多峰的形状,这种结果主要考虑波包和超晶格势分界面的相互作用后,电子波包相互叠加的结果.需要指出的是,在图3 中,波包在移动过程中伴随形状改变,主要表现为波包宽度变宽,中心强度减弱,这主要是波包的相速度与波包的群速度不一致导致的.对比图3(a),(b)可以看到,自旋向上电子对应的透射波包在超晶格中的隧穿时间明显长于自旋向下的情况,然而反射部分情况正好相反.更具体的变化关系见图4.

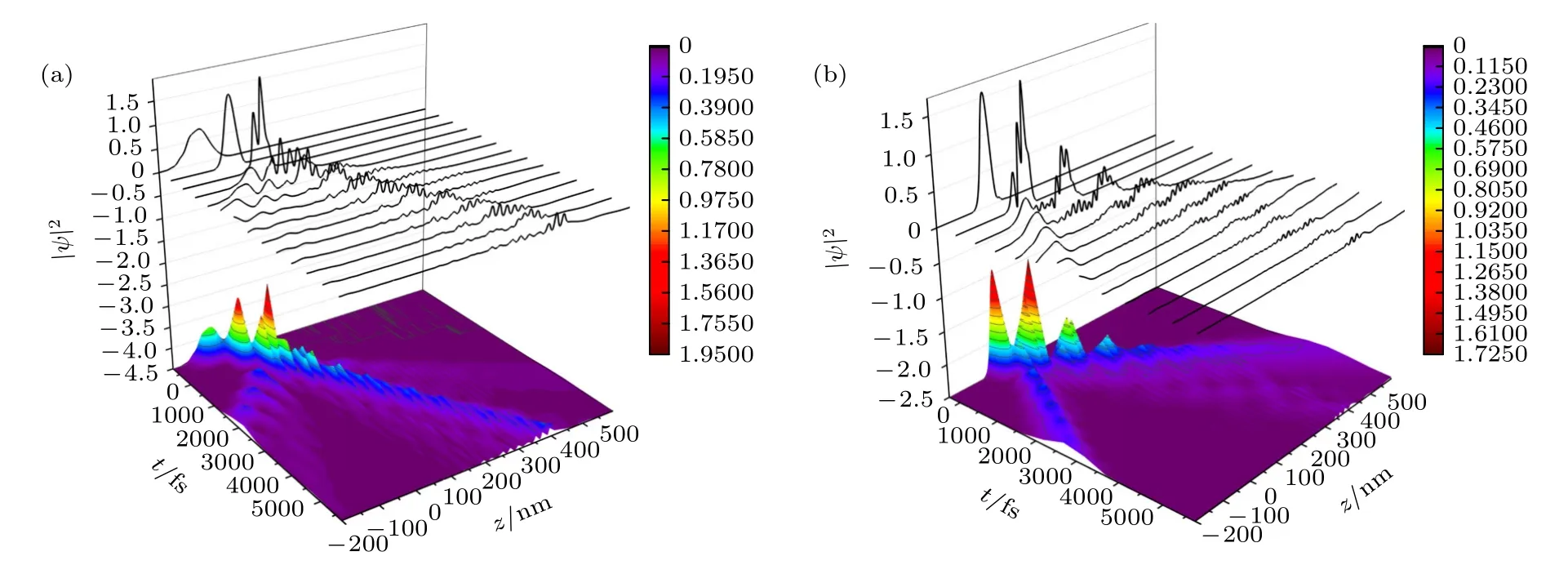
图3 稀磁半导体/半导体超晶格结构中,不同时刻不同自旋方向电子概率密度 |ψ(z,t)|2 随坐标z 的变化关系曲线 (a)自旋向上;(b) 自旋向下Fig.3.Spin-dependent electron probability density |ψ(z,t)|2 as a function of coordinate z for different times in the superlattices of dilute magnetic semiconductors/semiconductors structure: (a) Spin up;(b) spin down.

图4 稀磁半导体/半导体(DMS/S) 超晶格 结构中,位置z=-100,-10,205,415 nm 处,不同自 旋方向 电子概 率密度|ψ(z,t)|2随时间t 的变化关系曲线Fig.4.Spin-dependent electron probability density |ψ(z,t)|2 as a function of time t for different coordinates z=-100,-10,205,415nm in the superlattices of dilute magnetic semiconductors/semiconductors structure.

图4 给出了电子概率密度 |ψ(z,t)|2随时间变化的关系曲线.选取了结构中4 个位置进行了数值计算,分别是z=-100,-10,205和415 nm,其中超晶格所在范围为[0,410 nm],选择的4 个位置中z=-100,-10 nm 位于入射区,z=205 nm 位于超晶格中心处,z=415 nm 位于透射区.从图4可以看到,在z=-100 nm 处,概率密度先呈现出明显的高斯型波峰,然后被一段强度近似为零的间隙隔开,接着概率密度强度比开始高斯型波峰明显减弱(由0.7 减弱为0.26).图中可以明显看到在开始的高斯型波包部分自旋向上和自旋向下的概率密度是重合的,这是因为入射区为半导体材料,对于自旋向上和自旋向下电子的势函数是一样的,并且此时的概率密度只包含入射波包.强度近似为零的间隔区是入射波包已经通过z=-100 nm 处,反射波包还没到达的时间段.550 fs 后,电子概率密度开始逐渐增强,这是反射波包再次通过z=-100nm 处,反射波包通过时,自旋向上和自旋向下概率密度呈现出明显的不同.对于自旋向上的波包感受到的是势垒势,随着时间的推移,电子的概率密度呈现出几次大的振荡,然后逐渐趋于零,这是自旋向上电子在超晶格结构中各个界面处反射叠加最后反射回入射区的表现.对于自旋向下的波包因为感受到的是势阱势,在反射区只是出现了一次振荡,然后趋于零,但是概率密度强度与自旋向上时最大强度几乎相等.在z=-10 nm 处,这个位置距离超晶格结构更近,因此在概率密度随时间变化曲线中没有出现z=-100 nm 处强度几乎为零的间隔区间,也就是这个位置的入射波包与反射波包没有空间上的分离.电子的概率密度表现为:自旋向上电子的概率密度仍然可以看到在到达最大值后伴随有几个振荡峰,但是自旋向下的没有出现随后的伴随峰.在超晶格结构中心z=205nm 处,自旋向上和自旋向下电子的概率密度在t=900 fs 时开始增强,随后都出现了明显的振荡峰.不同的是,自旋向上的振荡峰明显多于自旋向下,并且自旋向上的概率密度最大值出现在t=3270fs 时,自旋向下的最大值明显早于自旋向上的情 况,出现在t=1390 fs 时.在透射 区z=415nm 处,自旋向上和自旋向下的电子概率密度在t=1820 fs 时开始增强,其中自旋向下的概率密度的最大值出现在t=2780 fs 时,自旋向上的最大值明显滞后于自旋向下的情况,出现在t=5850fs 时.此外,与前面不同位置的区别在于,此时的振荡峰不再是分立的单峰的形式,出现这种现象的主要原因是随着时间的增加,波包扩散开始显著,表现在波形上就是形状发生明显改变[32].通过以上数值计算结果可以比较容易的得到波包到达超晶格结构各处的时间和隧穿通过的时间,这些结果对优化设计基于超晶格结构的高速量子隧穿器件有一定的理论指导意义.

4 结论

理论研 究了由 Zn1-xMnxSe/ZnSe 组成的稀磁半导体/半导体超晶格结构中电子的自旋输运性质,数值计算结果显示,光场和磁场对该结构中电子自旋输运有显著的调控作用,主要表现在: 考虑光场辐照时,共振带会随着光场强度的增大而出现变形,同时伴随共振带展宽.对于较强磁场的情况,在不加光场时,低能区透射系数几乎为零,但是随着光强增强,低能区透射系数明显增大,即出现了准束缚能带,这些特征源于电子在隧穿经过光辐照下的超晶格结构时与光场发生了能量交换,比如低能区域的电子可以通过吸收光子进入共振能带从而完成完全透射,这样在低能区形成准束缚能带.此外,光场和磁场可以明显改变电子的自旋极化度.一定磁场强度下,光场的引入使电子的自旋极化度发生了明显变化,主要表现在自旋极化平台宽度变窄同时在平台两侧伴随着振荡峰的,随着光场强度的增大,这种影响加强,从而可以实现光场对自旋极化的调制.此外通过对高斯波包在该结构中演化的数值计算,可以清楚地了解不同自旋方向电子在其中的隧穿时间,同时可以看到在该超晶格结构中,自旋向下的电子隧穿时间明显比自旋向上的短,这些理论结果对设计基于超晶格结构的高速量子器件有一定的指导意义.