非周期二进制/M 进制信号激励下非线性系统的非周期共振研究*

王重秋 杨建华

1) (中国矿业大学计算机科学与技术学院,徐州 221116)

2) (中国矿业大学机电工程学院,江苏省矿山机电装备重点实验室,徐州 221116)

研究单一非周期二进制或M 进制信号激励下一类非线性系统的非周期共振现象及其度量方法,重点探讨了系统参数引起的非周期共振.提出了适用于非周期共振度量的响应幅值增益指标,并结合互相关系数和误码率展开研究.结果发现,互相关系数能够较好地描述系统输出和输入信号之间的同步性及波形相似性但无法刻画信号通过系统后被放大的程度.响应幅值增益能够较好地描述信号通过系统后幅值被放大的程度,但无法反映系统输出和输入信号之间的同步性及波形相似性.非周期共振发生在互相关系数取谷值和响应幅值增益取峰值处,且两种指标曲线反映的共振点相同.误码率在合适的阈值下可以描述系统输出和输入信号之间的同步性以及非周期信号通过系统后被放大的程度,误码率曲线可以直接给出非周期共振的共振区.单一非周期二进制或M 进制信号激励下的非线性系统可以发生非周期共振,其共振效果需要综合互相关系数、响应幅值增益、误码率等指标进行度量.

1 引言

非周期信号广泛存在于自然界和工程领域.非周期二进制信号是非周期信号的一种典型形式,在通信技术[1]、激光物理[2,3]、图像处理[4,5]等领域广泛使用.已有的研究文献对周期信号激励下非线性系统的响应研究较多,如随机共振[6–10]、振动共振等现象[11–13].非周期信号激励下,非线性系统响应呈现复杂的动力学行为,典型的现象有非周期随机共振[14–16]、非周期振动共振[3,17,18]等,这些非线性现象及机理为非周期信号处理提供了新的途径.

Duan 等[19]在离散的Hopfield 神经网络中研究了非周期二进制信号的传输问题,基于非周期随机共振提高了信号传输效率.Kang 等[20]研究了色噪声和非周期二进制信号激励下神经元系统的信息处理过程,基于系统响应的非周期随机共振理论,发现了噪声在非周期信号处理过程中的积极作用.Zhao 等[21]和Huang 等[22]基于阵列非周期随机共振进行了图像降噪自适应处理,提高了噪声背景下图像的处理信噪比和处理效率.非周期M进制信号是非周期二进制信号的拓展形式,其在工程领域应用同样广泛.M进制信号激励下非线性系统的非周期共振呈现更复杂的共振形式.Zeng 等[23]和Liang 等[24]分别研究了不同噪声背景下M进制信号的随机共振及信号检测问题,探索了噪声的积极作用.McDonnell 和Gao[25]研究了M进制信号激励下系统的超阈值随机共振,研究结果对多传感器的信号处理具有参考价值.Cheng 等[26]研究了信号相关噪声激励下多级阈值系统中的超阈值随机共振,研究结果有助于理解生物感觉系统的编码机制.在更广泛的范围内研究非周期信号激励下系统的随机共振,有利于解决旋转机械设备故障诊断[27]、磁场异常检测[28]、钢丝绳无损探伤[29]等领域的工程问题.

非周期二进制信号激励下的非线性系统,如果同时加入高频激励信号,系统响应会发生非周期振动共振现象[17].Chizhevsky 等[3,30]在基于非周期振动共振的激光系统微弱二进制信号检测方面做了较多的工作.Morfu 等[31,32]基于非周期振动共振进行图像处理研究,通过非周期振动共振进一步提高了含噪图像处理的效果.关于非周期二进制信号激励下系统的振动共振理论研究尚多,比如适用于快变非周期信号的变尺度方法以及二次采样方法[17,18],非周期振动共振的应用研究尚处于起步阶段.非周期M进制信号激励下非线性系统振动共振响应的文献尚未发现.

不管是非周期随机共振还是非周期振动共振的研究文献,侧重点往往是激励中的噪声或者起辅助作用的高频信号,侧重于由这两种因素引起的非周期共振现象.事实上,在非周期共振的研究中,非线性系统一般会起到更重要的作用.对于激励中不含有噪声或者高频辅助信号的情况,系统对单一信号的响应是否存在较强的非周期共振是非常值得探讨的问题.目前对于周期信号和调频信号激励下系统参数引起的共振已有相关研究成果[33–35].对于单一非周期二进制信号或M进制信号是否会引起系统输出的非周期共振响应尚无相关研究.只有弄清这一问题,才能为非周期二进制或M进制信号处理时选择非线性系统提供依据,开拓新思路和新方法,同时也能发现新的非线性动力学现象,拓展非线性动力学的研究成果.

本文结构安排如下: 第2 部分研究非线性系统对非周期二进制信号的响应,基于三种不同的指标探讨系统参数引起的非周期共振现象,并对每个指标的度量效果进行对比分析;第3 部分研究非线性系统对非周期M进制信号的响应,基于动力学响应的复杂性分析该种激励下非线性系统发生非周期共振的条件;第4 部分给出本文的结论.

2 非周期二进制信号引起的非周期共振

研究非周期信号激励下的过阻尼非线性系统

其中a和b为系统参数,s(t) 是非周期激励信号,本文分别考虑s(t) 为非周期二进制信号和非周期M进制信号两种情况.参数a,b取值不同,系统势函数具有不同的不动点,势阱形状呈现不同的稳态模式[36].

2.1 非周期二进制信号

非周期二进制信号的表达式为

其中A是信号 的振幅,Rm=1或-1 是符合 一定统计规律的随机数,本文采用符合高斯分布的随机数.函数Γ(t) 满足

其中,T是脉宽,即非周期信号s(t) 随机脉冲的最小宽度.

由于信号s(t) 的非周期性,导致信号具有一定的随机性,图1 给出了在幅值A和脉宽T取值一定时s(t) 的3 种不同波形.为方便描述,图中的3 种波形对应的信号自上而下依次命名为Signal 1,Signal 2,Signal 3,(1)式中Rm序列的不同导致信号波形的不同.

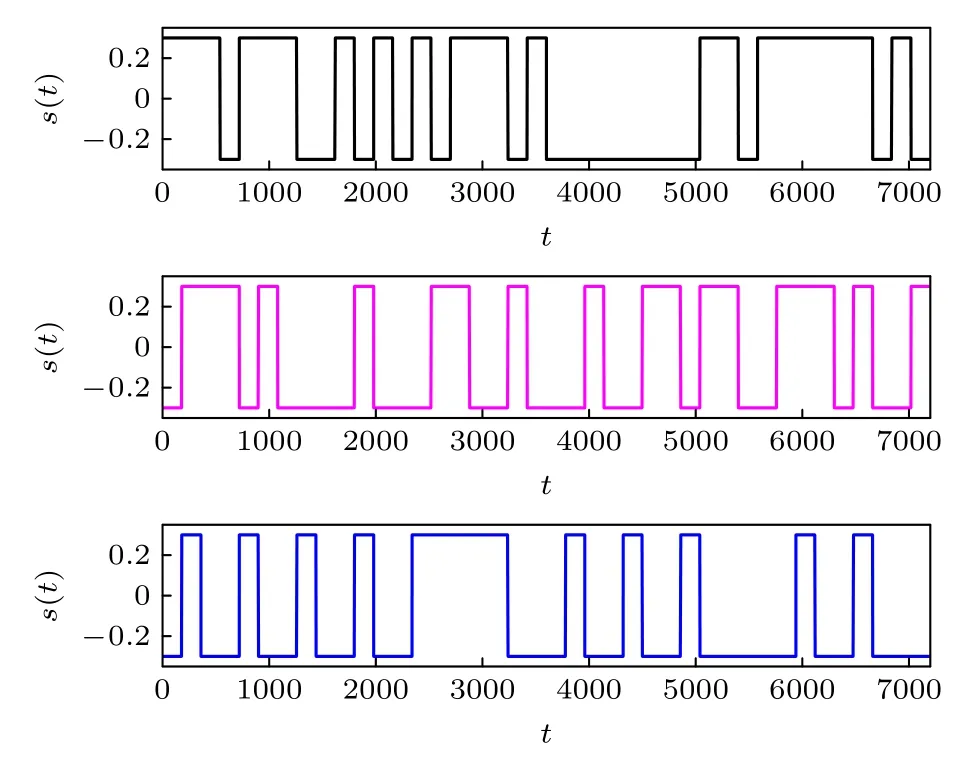
图1 A=0.3,T=100 时,非周期二进制信号的不同时域波形.自上而 下信号 分别标记为Signal 1,Signal 2,Signal 3Fig.1.Different waveforms of the aperiodic binary signal at A=0.3,T=100.The signals are labeled as Signal 1,Signal 2,Signal 3 from top to bottom.

2.2 非周期共振分析

在研究非周期二进制信号引起的随机共振和振动共振现象时,一般以系统输出x(t) 和输入信号s(t)之间的互相关系数作为指标.互相关系数为

其中m为时间序列的总长度,s¯和x¯ 分别为时间序列的均值.

针对图1 中给出的3 种信号,图2 给出了互相关系数Csx和系统参数a之间的关系曲线.从图2可见,信号波形的差异不会导致互相关系数曲线的本质变化.也就是说,在图1 给定的3 种信号下,图2中Csx-a的变化规律基本一致.因此,后续分析采用一种波形信号即可.图2 中随着系统参数a的变化,相关系数呈现明显的变化趋势.在a从负值到正值变化的过程中,相关系数减小,并在a=1.05处达到极小值.之后,随着a值的进一步增大,在a=1.1 处达到峰值.事实上,互相关系数只能描述两个时间序列的同步性及波形的相似性,并不能刻画信号通过系统之后是否被放大.因此,还需要借助于时间序列或者其他指标进一步分析.

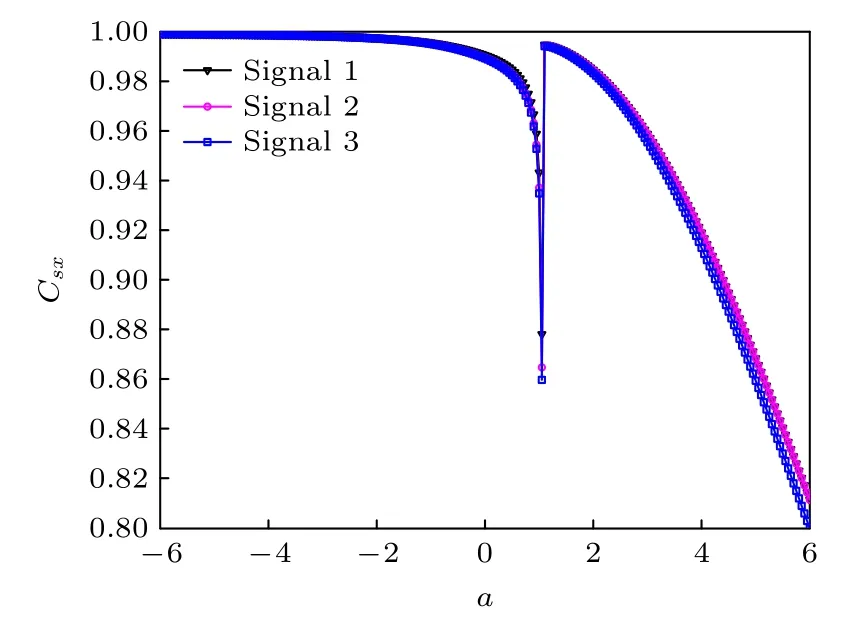
图2 b=2,A=0.3,T=100 时,不同波形的非周期二进制信号激励下,系统输出与输入信号之间的互相关系数Csx 与系统参数a 之间的关系Fig.2.Cross-correlation coefficient Csx between the system output and input signal versus the system parameter a under the excitation of aperiodic binary signal with different waveforms at b=2,A=0.3,T=100.

图3 给出了系统参数a取值不同时,系统响应的时间序列.从时间序列上看,每一幅子图上输出和输入的波形相似性较大,这是图2 中相关系数取值较大的原因.此外,相关系数小于1 的原因是系统的输出和输入之间存在一定的相位滞后,造成在时域上输出波形的变化和输入波形的变化并不完全同步.在图3(a)和图3(b)中,即当a=0 和a=1.05 时,系统输出呈现非周期共振状态,输出信号相较于输入信号被放大.图3(b)中的共振最强,对应于图2 中相关系数取极小值,即相关系数曲线取谷值的情况.在图3(c)和图3(d)中,虽然输出信号和输入信号之间的相似性仍较高,但其响应幅值未被系统放大.图3(c)的参数取值对应于图2 中相关系数取峰值的情况.图中反映的结果和之前类似的研究是不同的,比如在之前随机共振和振动共振的研究中,最强的共振往往出现在相关系数取峰值的情况[3,14–18].

图3 b=2,A=0.3,T=100 时,系统参数a 取值不同时输出的不同波形 (a) a=0 ;(b) a=1.05 ;(c) a=1.1 ;(d)a=2Fig.3.Different waveforms of the output under different values of the system parameter a with b=2,A=0.3,T=100:(a) a=0 ;(b) a=1.05 ;(c) a=1.1 ;(d) a=2 .

从以上图2 和图3 的分析中发现,基于相关系数很难直接反映信号被放大即系统响应发生非周期共振的情况,时间序列也仅能从有限的算例直观反映系统的输出,不能给出通用性更强的结论.为了更好地刻画非周期共振,需要新的指标.因此,此处提出响应幅值增益指标,其计算公式为

其中符号max 和min 分别表示取最大值和最小值.结合图2 中的时间序列容易理解(5)式的物理意义,其中可以直观理解为响应的幅值,很明显β 为系统输出和输入信号之间幅值的比值.值得一提的是,在计算β 时,x(t)应该截掉初始条件x(0) 引起的瞬态响应,否则影响输出的准确性.虽然(5)式中计算响应幅值增益指标具有一定的近似性,但其在大部分情形下能从本质上说明信号通过系统后振幅被放大的倍数.

根据(5)式的计算公式,图4 给出了系统的响应幅值增益β 与系统参数a之间的函数关系曲线,图中很好地显示了系统的共振以及信号幅值被放大的情况.图中共振发生在a=1.05 处,此时β=2.8,说明非周期二进制信号通过系统后幅值被放大了2.8 倍.进一步地,共振点对应的位置a=1.05也对应于图2 中相关系数取极小值点,即取谷值的点.对比响应幅值增益和相关系数曲线呈现的规律,相关系数主要是反映输出和输入之间的同步性,并从侧面对共振的分析提供参考;响应幅值增益直接反映系统输出和输入信号之间的幅值变化情况,不能直接反映系统输出和输入信号之间的波形是否同步变化,假设系统输出和输入之间存在较大的滞后甚至反相,不会影响幅值增益β 的值,但会明显影响相关系数Csx的值.因此,互相关系数和响应幅值增益仅各从一个角度反映系统输出的情况.

图4 b=2,A=0.3,T=100 时,响应幅值增益β 与系统参数a 之间的函数关系Fig.4.Response amplitude gain β versus the system parameter a with b=2,A=0.3,T=100.

为了更好地揭示系统输出x(t) 随系统参数a的变化情况,此处引入另一个指标,即误码率(bit error rate,BER),误码率也可以用于描述系统的共振行为[37].对于误码率的计算,如何定义输出被正确接收和错误接收的码元将直接影响误码率的值.众所周知,系统输出幅值一般不等于输入信号的幅值.如果输出的幅值绝对值大于给定的阈值Ath就认为码元接收正确,反之则错误.因此,阈值Ath的选择也至关重要.不同的阈值对应不同的物理意义,此处分别选择两种典型的阈值,即Ath=0和Ath=A.显然,Ath=0 意味着输出和输入之间的正负一致,这确保了输出和输入信号之间的同步性.在此基础上,如果再满足Ath=A,就能够保证系统输出和输入在同步的基础上幅值被放大.基于这种计算思想,图5 给出了在两种不同阈值Ath情况下,误码率BER 与系统参数a之间的函数关系曲线.图5 中关于参数a的数值计算步长为 0.05 .对应于Ath=A,当a≤-0.85时BER=1,这说明信号完全没有被放大;而对应于Ath=0 ,BER=0,说明输出波形和输入波形完全同步.在a∈[-0.8,1.05] 区间上,对应于Ath=A和Ath=0 的两条曲线值接近,且都接近于0,这说明在这段区间上系统能够发生较强的非周期共振现象,即输出能够保持和输入信号波形的相似性又能够被放大.对于a＞1.1 的情况,两条曲线重合且误码率保持为0.45,这说明一部分信号被放大而另一部分信号被错误接收,如图3(c)和图3(d)的输出情形.在误码率曲线上,a∈[-0.8,1.05] 被认为是比较强烈的非周期共振区间.对于a≥1.1 的情况,两条误码率曲线几乎完全重合,这主要是由于输出向一个势阱内漂移并在一个势阱内振荡,使输出和输入之间的正负不再完全同步,导致BER 取相对较大的值.

图5 b=2,A=0.3,T=100 时,误码率BER 与系统参数a 之间的函数关系Fig.5.Bit error rate (BER) versus the system parameter a with b=2,A=0.3,T=100.

互相关系数、响应幅值增益、误码率在反映非周期共振方面都有一定的适用范围和相应的优势,这3 种指标也能反映一定的共性规律,比如3 种函数指标曲线都显示当a=1.05 时系统输出会呈现较强烈的非周期共振现象.

3 非周期M 进制信号引起的非周期共振

3.1 非周期M 进制信号

非周期M进制信号为s(t)=Am,m=1,2,···,s(t) 在每个 码元的 振幅为Am=(2m-1-M)A,且服从给定的概率分布,此处令Rm满足均匀分布.当(2)式中的随机数Rm的选择范围从 -1和1 扩大到 2m-1-M中的任意数时,非周期二进制信号扩展为非周期M进制信号.在信号参数取值一定时,图6 中给出了M进制信号3 种不同的波形.在本部分,图中的3 种波形对应的信号自上而下命名为Signal 4,Signal 5,Signal 6.

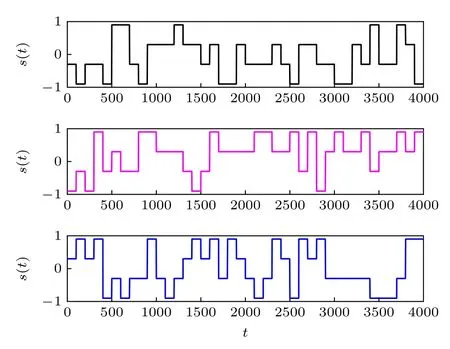
图6 M=4,b=2,A=0.3,T=100 时,非周期M 进制信号的不同时域波形.自上而下信号分别标记为Signal 4,Signal 5,Signal 6Fig.6.Different waveforms of the aperiodic M-ary signal with M=4,b=2,A=0.3,T=100.The signals are labeled as Signal 4,Signal 5,Signal 6 from top to bottom.

3.2 非周期共振分析

针对图6 中给出的3 种信号,图7 给出了互相关系数Csx和系统参数a之间的关系曲线.由于输入信号波形的差异,导致相关系数最小值的具体取值存在一定差异,这和信号长度选取有关,当信号选取足够长时这种差异可以消失.相关系数最小值的微小差异不影响其对应的系统参数a取值,不影响系统参数引起的非周期共振基本规律.图7 说明非周期M进制信号波形的不同不会导致Csx与a之间关系曲线的本质变化,因此本部分对M进制信号的共振分析以一种信号波形为例即可.以Signal 4 为例,分析相关系数随着a的变化趋势,在a=2.2 处相关系数达到极小值,即谷值,在a=3处相关系数达到峰值.

图7 M=4,b=2,A=0.3,T=100 时,不同波形的非周期M 进制信号激励下,系统输出与输入信号之间的互相关系数 Csx 与系统参数a 之间的关系Fig.7.Cross-correlation coefficient Csx between the system output and input signal versus the system parameter a under the excitation of aperiodic M-ary signal with different waveforms at M=4,b=2,A=0.3,T=100.

为了进一步探究系统输出的共振情况,图8 给出了系统参数a取值不同的情况下系统输出的波形.参数a的取值主要参考了图7 中对应相关系数的取值情况.图8(a)对应于图7 中相关系数曲线到达极小值之前的情形,时间序列反映了输出和输入之间存在一定的同步性,但部分信号幅值不仅没有被放大,反而比之前的幅值小.图8(b)对应于图7 中的曲线极小值,对应的时间序列是图8 的4 幅子图中非周期共振效果最强的.图8(c)对应于图7 中的曲线峰值,此时虽然输出和输入信号的波形相似性较好,但输出被限制在一个势阱之内,输出的幅值较小.在图8(d)中,输出仍然被限制在一个势阱之内,信号幅值进一步缩小.相较于非周期二进制信号的情形,非周期M进制信号激励下非线性系统的输出呈现更加复杂的特性,输出难以达到既和输入信号波形相似又被放大的效果.

图8 b=2,A=0.3,T=100 时,系统参数a 取值 不同时输出的不同波形 (a) a=0 ;(b) a=2.2 ;(c) a=3 ;(d)a=5Fig.8.Different waveforms of the output under different values of the system parameter a with b=2,A=0.3,T=100: (a) a=0 ;(b) a=2.2 ;(c) a=3 ;(d) a=5 .

参照(5)式计算响应幅值增益的方法,将(5)式改造为可以计算M进制信号引起的响应幅值增益的公式

从系统的输出时间序列(如图8 中的时间序列)可以发现,系统的输出不再是M个码元,而是会进一步增加码元的个数,因此响应幅值增益改进为(6)式的形式.显然,由于输出中码元的增多以及各码元的相对位置变化较大,(6)式是一种均值意义上的估计,能够大致反映M进制信号输入系统后对应的输出被放大的程度.

图9 给出了响应幅值增益与系统参数a之间的函数关系,β-a曲线呈现明显的共振现象.共振发生在a=2.2 处,对应于图7 中相关系数曲线的极小值即波谷位置,这说明通过互相关系数和响应幅值增益反映的共振点是一致的.图9 的响应幅值增益曲线能够更好地反映信号通过系统后被放大的情况,图中的峰值处β=1.35,这说明信号通过系统后发生非周期共振后信号在一定程度上被放大,但信号幅值并不会在很大程度上被放大.

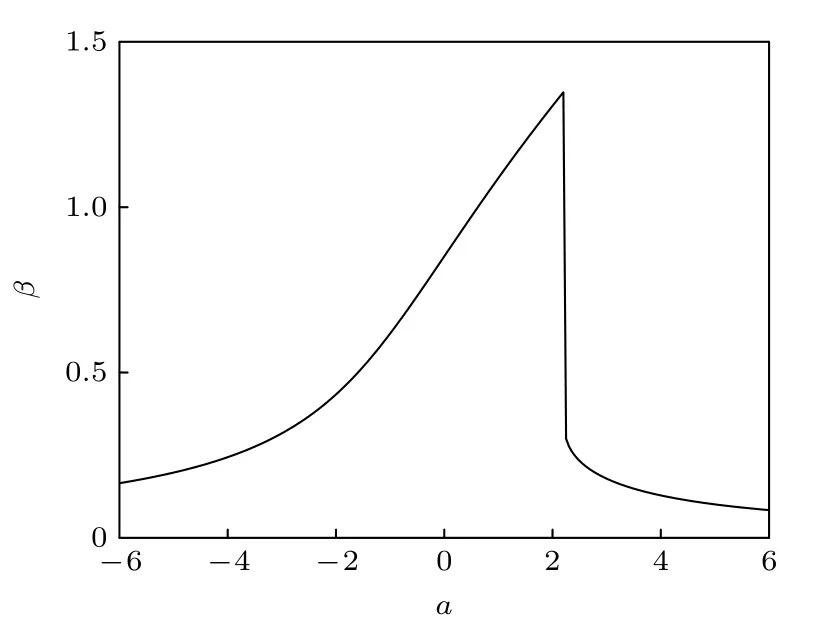
图9 M=4,b=2,A=0.3,T=100 时,响应幅值增益β 与系统参数a 之间的函数关系Fig.9.Response amplitude gain β versus the system parameter a with M=4,b=2,A=0.3,T=100.

以误码率为计算指标,图10 为误码率BER与系统参数a之间的关系曲线.对应于Ath=0 的误码率曲线刻画了输出和输入之间同步变化的情况,对应于Ath=A的误码率曲线既刻画了输出和输入之间同步变化又刻画了信号通过系统后被放大的情况.曲线Ath=A取小值的区间是非周期共振较强烈的区间,比如图7中a∈[0.65,1.05] 的区 间.当a≥0.65 时,对应于Ath=A和Ath=0 的曲线基本重合.a取值在0 和1 之间,误码率曲线呈现阶梯状水平线,这既说明系统输出和输入信号之间的波形存在一定的相似性,又说明系统输出中仅部分信号相较于输入信号的幅值被放大.

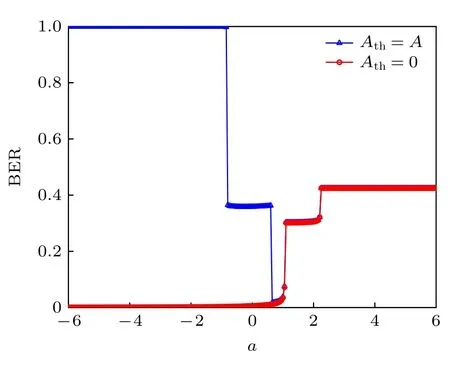
图10 M=4,b=2,A=0.3,T=100 时,误码率BER 与系统参数a 之间的函数关系Fig.10.Bit error rate BER versus the system parameter a with M=4,b=2,A=0.3,T=100.

为了进一步明确显示系统发生非周期共振时的系统输出情况,对应于图10 中的共振区选择不同的a值,图11 给出了对应的响应时间序列.图11的时间序列,相较于图8(b)—(d),输出呈现出更明显的同步性,输出能够在两个势阱之间随着输入同步翻转.图8(b)中有一小部分输出不能实现和输入信号在两个势阱间同步穿越,导致共振效果欠佳.图8(c)中的输出几乎都被限制在一个势阱内,共振效应进一步下降.对应于图10 中的共振区中的参数取值,图11 中的时间序列不存在上述问题,输出和输入之间的同步性较好,信号在一定程度上被放大.从图11 的时间序列进一步发现,M进制信号激励下系统的非周期共振更侧重于对输入和输出之间同步性及码元接收正确性的一种描述,不再侧重于信号的放大效应.

图11 M=4,b=2,A=0.3,T=100 时,系统参 数a 处于共 振区时 输出的波形 (a) a=0.65 ;(b) a=0.75 ;(c) a=0.85 ;(d)a=0.95Fig.11.Different waveforms of the output when the system parameter a lies in the resonance region with M=4,b=2,A=0.3,T=100: (a) a=0.65 ;(b) a=0.75 ;(c) a=0.85 ;(d) a=0.95 .

对比非周期二进制信号引起的共振和非周期M进制信号引起的共振,发现系统参数的变化均能引起非周期共振现象,且两种信号引起的非周期共振程度可以用相同的指标进行描述,反映共振规律的曲线具有相似的特点.然而,非周期二进制信号引起的共振能够达到更强的共振程度,而非周期M进制信号引起的共振程度相对较弱.这是因为非周期二进制信号波形相对简单,经过系统后虽然输出信号幅值发生了变化,但一般情况下仍保持为非周期二值信号,而非周期M进制信号经过系统后一般会增大M的值,即输出信号取值多于M个值,这就造成了输出信号波形难于和输入的M进制信号匹配,因而从度量指标和输出波形上反映的共振程度较弱.

4 结论

分别以非周期二进制信号和非周期M进制信号作为输入信号,研究单一非周期信号激励下非线性系统的响应行为,重点讨论非周期共振现象及其度量方法.研究主要得到了以下结论:

1)在单一的非周期二进制信号或者非周期M进制信号激励下,通过调整系统参数,非线性系统的输出能发生非周期共振.当非周期共振发生时,系统输出和输入信号之间保持较好的同步性,即系统输出在势阱内的穿越和输入信号的正负变化也同步,且系统输出的幅值比输入信号幅值增大.

2)为了更好地度量非周期共振效果,分别采用了互相关系数、误码率作为指标,并提出了响应幅值增益指标.互相关系数指标能够较好地刻画输出和输入之间同步性与波形相似性,无法直接判断输出是否发生了非周期共振,但可以辅助判断非周期共振的发生.针对采用的两种形式的非周期信号,非周期共振点均在互相关系数取极小值即波谷的位置.响应幅值增益指标可以直接刻画系统输出的幅值相较于输入信号幅值被放大的情况,但无法描述系统输出和输入信号之间的同步性或波形相似性.以误码率作为非周期共振的度量指标,选择合适的阈值,误码率曲线既能反映系统输出和输入信号的同步性和波形相似性,也能描述信号的放大性,并在曲线上呈现明显的共振区.

3)从共振效果上看,非周期二进制信号引发的非周期共振比非周期M进制信号引发的共振更强烈,这是由非周期M进制信号本身的复杂性以及通过系统后输出的复杂性导致的.

不论是比较简单的非周期二进制信号还是更复杂的非周期M进制信号引起的非线性系统响应,如果要明确地描述系统的非周期共振现象,应该选择多个指标从多个角度进行描述,同时考虑不同指标对非周期共振效果的影响.通过选择不同的非线性系统、采用优化算法实现适应度函数最优化、综合考虑非周期随机共振、振动共振、系统共振等多种共振模式,有望进一步提高系统的共振效果.本文虽然只考虑了系统参数对非周期共振的影响,但发现了单一非周期信号激励下非线性系统的非周期共振这种之前未被明确提出的新现象,并对非周期共振效果的度量给出了多个指标和多种方法.以本文的研究为基础并通过进一步拓展,还可以深入探讨不同非线性系统以及更多形式的非周期信号引起的非周期共振新现象、提高共振效果的新方法、以及在不同物理背景下的新应用.