基于患者数据的移动中位数法在实验室血清钙和磷检测质量控制中的应用

周朝琼，王华丽，孔丽蕊，何大海，黄 英，吴 风，张 艳

（1.成都市郫都区中医医院检验科，成都 611730；2.成都中医药大学附属第三医院检验科，成都 610031）

质量控制在临床实验室质量管理体系中占据重要地位。实验室内部质量控制(internal quality control，IQC )已成为大多数实验室质量控制的中心支柱，大多实验室依靠IQC反映患者结果可靠性[1]。但质控品成本高，存在基质效应，且监控时间局限等，可能无法准确反映患者样本的真实情况。随着实验室信息化的普及，基于患者的实时质量控制(patient-based real-time quality control，PBRTQC)近年来被认为在质量控制中最具价值和发展方向[2]，是IQC的一个有价值的补充。PBRTQC方法包括多种，如移动均值(moving average，MA)、移动中位数(moving median，MM)、移动四分位(moving quartile，MQ)、移动标准差(moving standard，MovSD)、指数加权移动平均(exponentially weighted moving average，EWMA)等。除MA外，其余方法均较适用于非正态分布数据[1]，但对项目选择、计算方法及适用的群体目前暂无统一标准[3]。本研究应用MM原理计算患者MM值，将MM与IQC进行比较，旨在评估基于患者数据的MM法对血清钙( calcium，Ca)及血清无机磷（phosphorus，P）的失控判断能力和及时性。

1 材料与方法

1.1 研究对象 收集2022年2月～2023年1月在成都市郫都区中医医院就诊患者的血清Ca和P检测数据各31 924例，同时收集上述项目同期内的质控数据，患者数据剔除离群值后分别为31 624，31 380例。按项目检测时间先后排序，将前半年数据（2022年2月～2022年7月）及IQC结果作为训练组用于实验设计，后半年数据（2022年8月～2023年1月）及IQC结果作为测试组用于实验验证。根据训练组数据在测试组做移动中位数质控图、Z分数质控图，同时根据westgard中的22S和13S规则判断失控情况。

1.2 仪器及试剂 项目检测仪器为Hitachi Labospect 008AS全自动生化分析仪，IQC来自美国伯乐公司，试剂及校准品均来自四川迈克公司。

1.3 方法

1.3.1 移动中位数（MM）计算方法：计算每天结果的日中位数（M），以连续7日（天）的M值计算1个MM，即1～7天计算一个MM，2～8天计算一个MM，以此类推，得到连续的数个MM值。将训练组MM最大值及最小值分别作为测试组控制上下限，超过二者即为失控，即移动中位数法。

1.3.2 Z值转换方法：将患者训练组MM的中位数（）及标准差（s）设定为测试组的靶值和标准差，并转换为Z值，绘制Z分数图，转换公式为Z=(MM-)/s。同理将IQC训练组的中位数()及标准差（s）设定为测试组的靶值和标准差，转换并绘图，转换公式为：Z=（C-）/s，C为每天的IQC结果。

1.4 统计学分析 用SPSS 25.0及Microsoft Excel进行数据分析及作图。K-S法进行正态分布检验，卡方检验用于MM及IQC对系统误差及随机误差检出次数是否有差异。标准差法剔除离群值，即测定值超过均值±3倍标准差则认定为离群值。

2 结果

2.1 样本情况分布表 见表1。剔除离群值后，血清Ca和P训练组及测试组样本分别为15 911，15 713例及15 783，15 597例。训练组及测试组总体分布一致，二者均为非正态分布（均P＜0.05）。

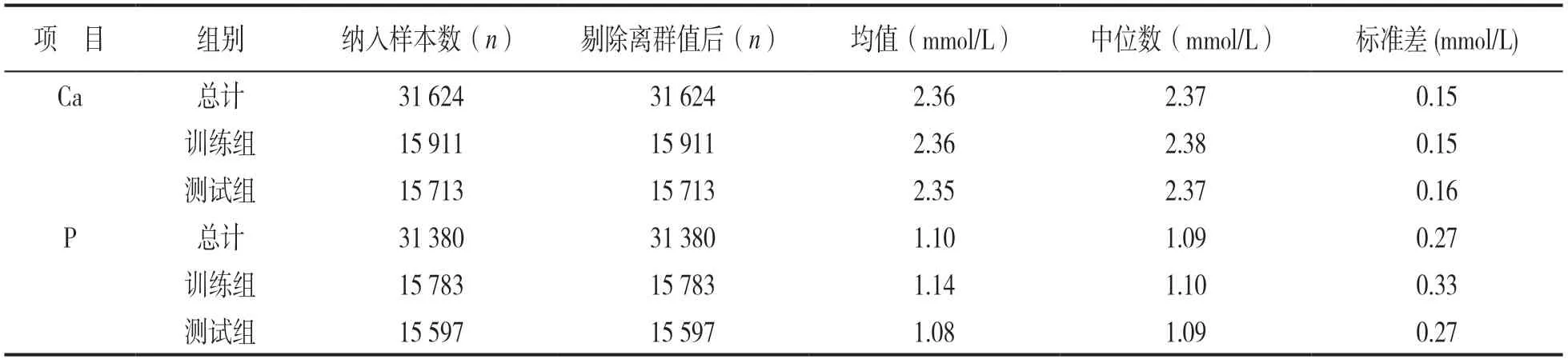
表1 样本情况分布表

2.2 血清Ca和P移动中位数法质控图

2.2.1 血清Ca移动中位数法质控图：训练组血清Ca最大和最小的MM值分别为2.43mmol/L，2.30mmol/L，将其分别作为测试组上下控制线，结果见图1。2022年11月30日～12月6日及12月14日～12月28日检测到Ca超过控制线，Ca移动中位数检测到超过控制线共22次，其中7次超过上限，15次超出下限。

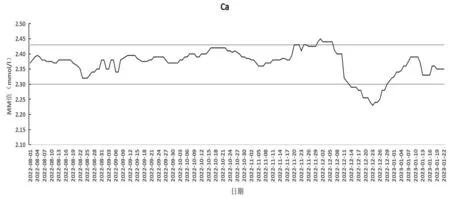
图1 Ca移动中位数法质控图

P移动中位数法质控图：训练组P最大和最小的MM值分别为1.16mmol/L，1.06mmol/L，将其分别作为测试组上下控制线，结果见图2。2022年12月16日～2023年1月4日、2023年1月6日～1月10日及1月16日～1月22日检测到P超过控制，P移动中位数检测到超过位移次数为32次，均为超过下限。

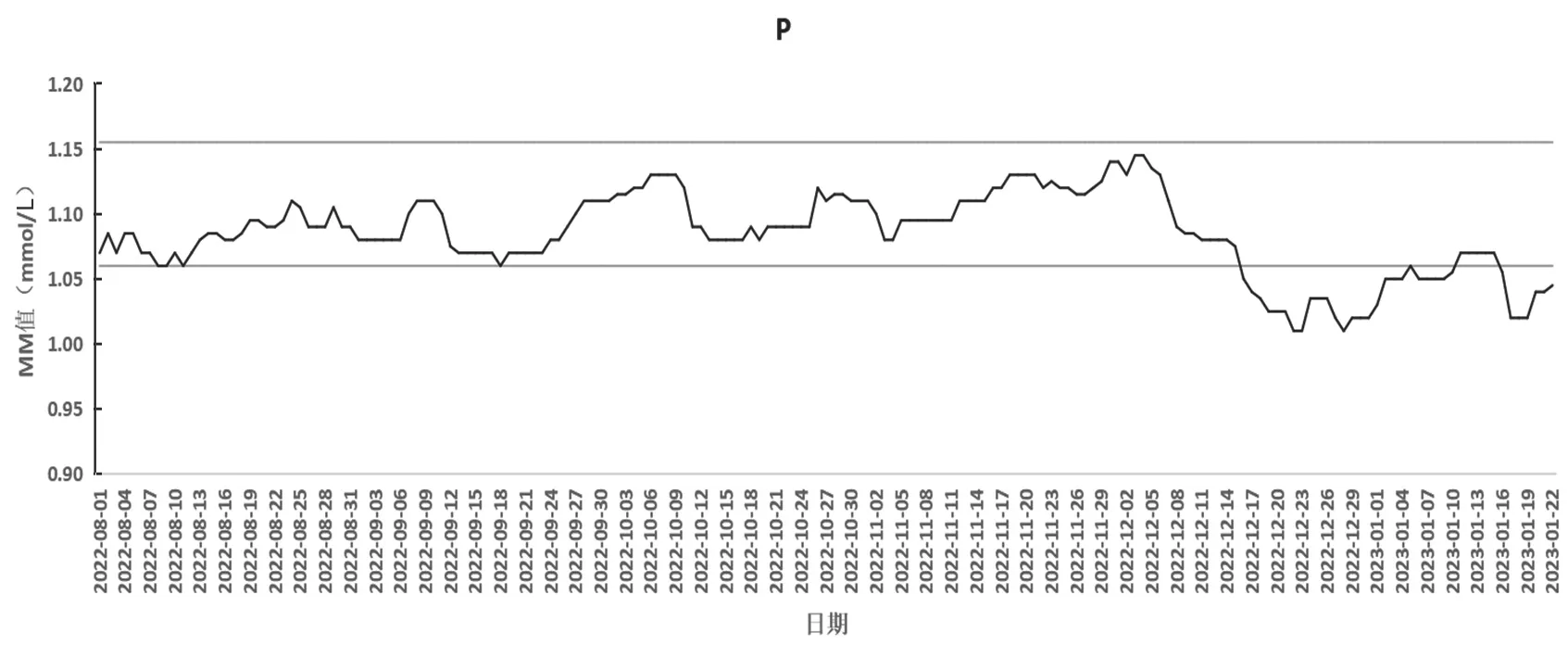
图2 P移动中位数法质控图

2.3 Ca和P 的Z值质控图

2.3.1 Ca的Z值质控图：Ca训练组M的中位数和标准差分别为2.38mmol/L，0.04mmol/L,将其分别设为测试组靶值及标准差，做Z分数图，结果见图3。根据westgard中的22S和13S规则，检测到系统误差33次，随机误差17次。

图3 Ca的Z值质控图

2.3.2 P的Z值质控图：P训练组M的中位数和标准差分别为1.09mmol/L，0.03mmol/L,将其分别设为测试组靶值及标准差，做Z分数图，结果见图4。根据westgard中的22S和13S规则，检测到系统误差23次，随机误差13次。

图4 P 的Z值质控图

2.4 IQC的Z值质控图

2.4.1 Ca的IQCZ值质控图：训练组IQC水平1和水平2中位数分别为 2.44mmol/L，3.16mmol/L，二者对应的标准差分别为0.04mmol/L，0.05mmol/L。将其分别设为测试组靶值及标准差，做Z分数图，结果见图5。IQC检测到Ca的系统误差和随机误差分别为7次和8次。

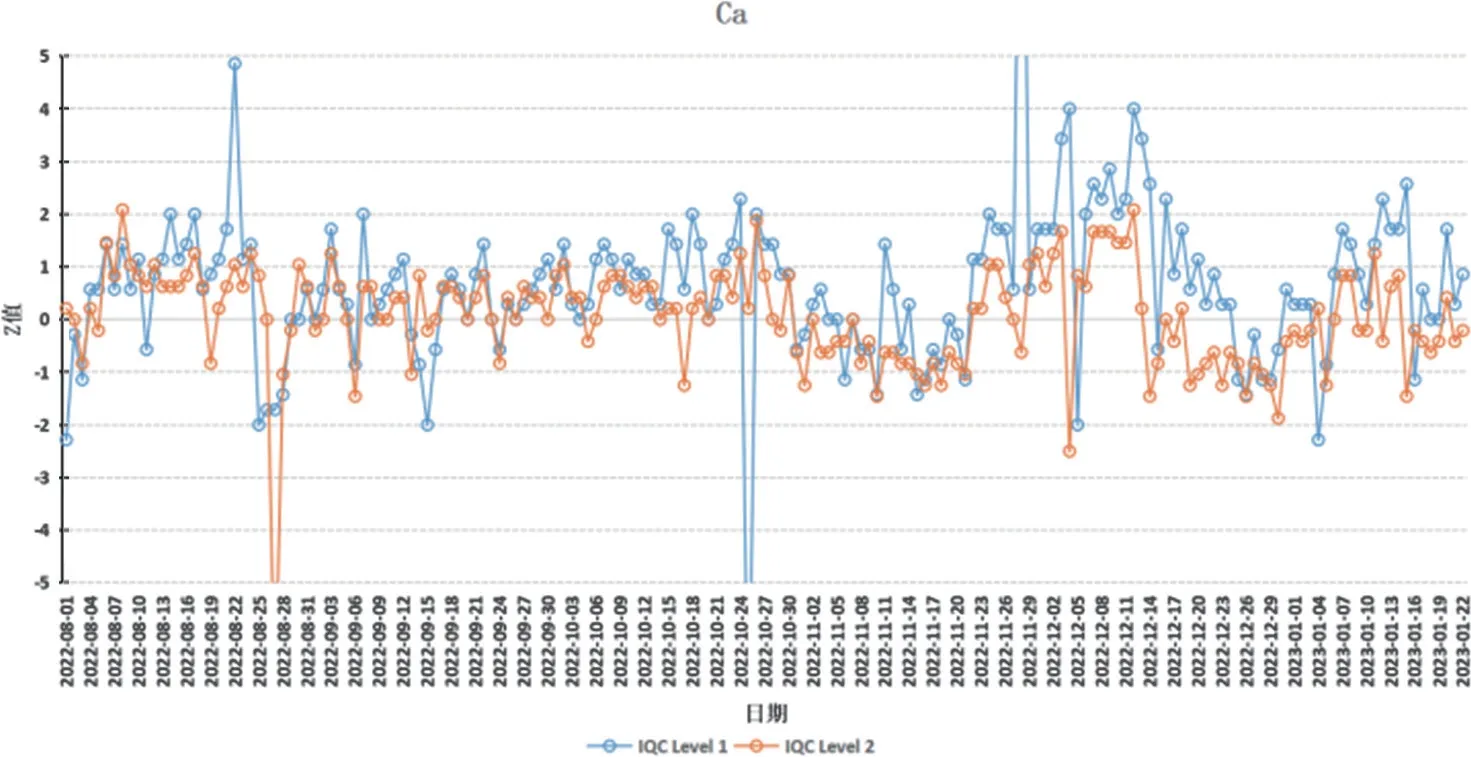
图5 IQC的Z值质控图

2.4.2 P的IQCZ值质控图：训练组IQC水平1和水平2中位数分别为 1.33 mmol/L，2.4mmol/L,二者对应的标准差分别为0.01mmol/L，0.03mmol/L。将其分别设为测试组靶值及标准差，做Z分数图，结果见图6。IQC检测到P的系统误差和随机误差分别为2次和4次。

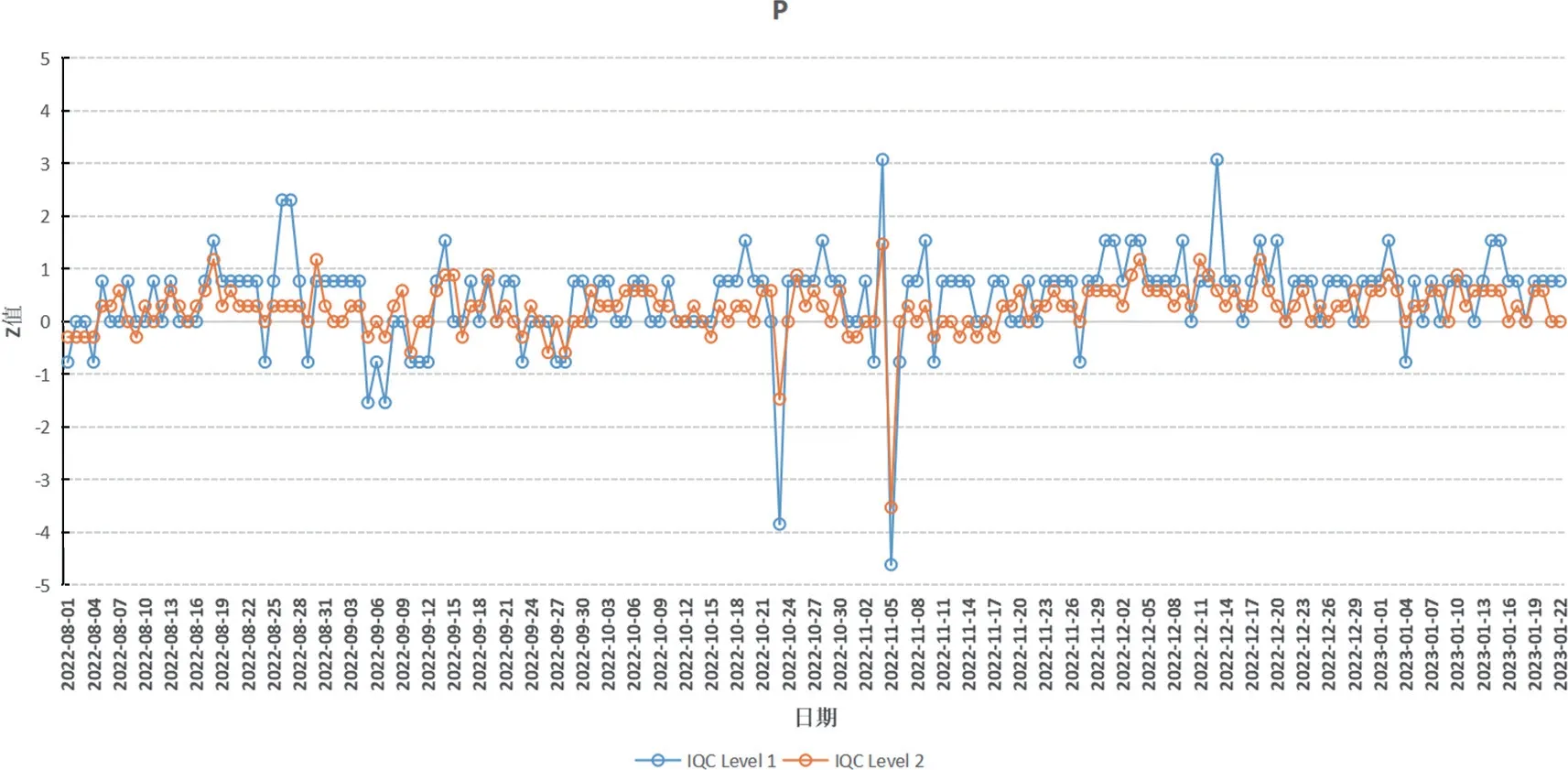
图6 IQC Z值质控图

2.5 MM及IQC失控判断能力的比较 根据westgard中的22S和13S规则，MM及IQC对Ca和P的系统误差及随机误差检出次数差异具有统计学意义（P＜0.05），见表2。MM对Ca和P系统误差及随机误差检出次数均优于IQC，但对随机误差识别时间晚于IQC。

表2 两种方法对失控判断能力比较表

3 讨论

大多实验室都通过建立IQC监测测量程序，虽IQC数据能提高实验室质量[4]，但大多实验室每天仅进行一次IQC[5]，国内将其称为初始IQC，其不足以快速检测到系统错误[6]，并影响患者结果，直到进行下一次IQC才被检出，甚至都未检出[7]。从而导致不同的临床决策，增加患者风险。虽可通过增加IQC频率提高系统错误检出速度，但增加了试剂耗材等消耗，从而造成医疗资源过度浪费。此外由于缺乏稳定的商业化IQC样品，一些测量程序并未进行IQC。

患者的实时质量控制(PBRTQC)具有矩阵效应小、成本低且不存在基质效应等优点，是一种有效的质控方法，其基本原理即是通过患者数据来识别分析系统稳定性[8-9]，如患者数据均值、中位数、标准差等。因其数据分析和处理较复杂且要求较高，故实验室应用较少[10-11]，但PBRTQC作为一种利用患者数据进行质量控制的方法，无基质效应，无检测时间局限等弊端，更能反映实验室真实情况，实验室应借助信息化，基于患者数据及IQC，提高结果准确性[12]，提高医疗质量，降低医疗风险。

虽有研究报道PBRTQC对项目计算方法目前暂无统一标准[3]，但谢叶红等[13]通过MM及MA两种方法对血脂的研究表明，二者总体趋势一致。在本研究中，我们对MM和IQC在Ca和P失控判断能力和及时性进行了比较，结果表明MM判断失控能力较IQC灵敏[13]，二者对失控判断的一致性较差，无论是系统误差还是随机误差的检出次数，IQC均不及MM，与张艳等[14]使用MA法结果略有差别，其研究结果表明IQC随机误差检出能力优于MA。有研究表明[15]，使用不同的标准来判断结果，可能会影响方案的有效性。同时因IQC存在基质效应，故可能无法及时准确地反应实验室检测结果的真实情况。虽本研究显示MM对Ca和P的失控检出次数优于IQC，但有学者研究表明患者群体数据不稳定，个体间变异较大[16-17]，甚至与患者临床状态相关[18]，同时本研究还显示IQC对随机误差的识别时间早于MM，因此需结合二者优点提高检验结果准确性[2]。研究中MM法2022年12月开始Ca，P均出现偏低且失控，提示可能为系统误差导致偏移趋势，经回顾发现此时间段实验室更换新批号质控品。本研究局限性在于仅对Ca和P进行分析，检测指标局限；但研究基于患者数据进行实时质量控制，仅需对患者数据进行分析，不需消耗额外试剂及耗材，不仅能使医疗资源应用最大化，还能更准确反映患者结果的可靠性，可在临床较好地推广应用。

综上所述，MM对实验室工作人员监测测量状态来说是一种有效手段，对提高实验室质量管理也较实用,可作为IQC的一种有效补充。