电子设备耦合刚度对QFP器件振动可靠性的影响

付永辉, 王琼皎, 董 锋, 刘江涛

(空间电子信息技术研究院 空间电子产品制造中心,西安 710100)

随着电子设备功能的日趋复杂,由多个模块互连实现某种功能成为普遍状态[1-3],互连方式如结构间的螺钉连接、锁紧压接,电路间的软电缆互连、半刚性电缆互连、连接器互连等,从结构动力学的角度考虑,这些物理连接产生的耦合刚度将导致电子设备整机动力学特性的变化,在开展力学设计及仿真分析时必须要予以充分考虑,但涉及此方面的公开文献资料很少。

四角扁平封装(quad flat package,QFP)作为表面组装技术中较早发展起来的封装技术,因其技术成熟,使用可靠性较高,目前在航天、航空等行业中应用较多[4-8]。QFP封装的引线从四个侧面引出呈海鸥翼型,引线焊接于印制板上,电、力学、热等载荷均通过引线、焊点传递,因此QFP封装器件力学可靠性的关注重点无疑就是引线和焊点。在振动、冲击等力学环境下,需要对QFP封装器件点胶加固以确保其引线、焊点的安全可靠[9]。但在器件层面的工艺加固并不能完全保证力学可靠性,如果电子设备因设计不合理或载荷过大,也可能造成器件的损伤失效,因此要确保器件的可靠性,必须要对电子设备结构设计的合理性开展仿真验证或试验验证。

文章首先基于结构动力学理论探讨了互连耦合刚度对隔振特性的影响;然后以某电子设备在振动试验后QFP器件引线断裂为例,开展了不同耦合状态的理论分析,并通过有限元仿真进行了验证;其次,分析了QFP器件的振动响应,并基于Palmgren-Miner累积损伤理论计算了器件引线的疲劳寿命;最后基于隔振理论提出了改进措施,保证了电子设备的力学可靠性。

1 互连耦合隔振理论

对于典型的数字类电子设备,每个功能模块的基本结构由机壳(机箱)和印制板组件组成,根据载荷传递的特点可将单个模块简化为两自由度系统,由于阻尼对系统的固有频率影响很小,暂不考虑系统的阻尼,如图1所示。图1中:m1,k1为机壳的质量及刚度特性;m2,k2为印制板组件的质量及刚度特性,该两自由度系统的固有特性可由式(1)确定[10]

图1 两自由度无阻尼基础激励系统Fig.1 Two-degree-freedom undamped foundation excitation system

(1)

则该系统的两阶固有频率为

(2)

(3)

(4)

(5)

化简式(5)可得

(6)

若要式(6)恒成立,则

(7)

对于由多个模块组成的电子设备,且模块间互连时,可简化为如图2所示的三自由度系统力学模型。图2中:m3,k3为其余模块的等效质量及刚度特性;kj为模块间的互连耦合刚度特性,则固有特性由式(8)确定

图2 三自由度无阻尼基础激励系统Fig.2 Three-degree-freedom undamped foundation excitation system

(8)

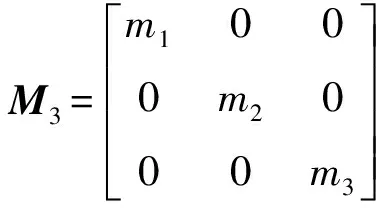
若模块间采用电缆、柔性连接器等柔性连接时,kj≪ki,i=1,2,3,即互连耦合刚度远小于结构刚度,该三自由度系统将退化为图1的两自由度系统和式(9)所示的单自由度系统。

(9)

若模块间采用螺钉连接、锁紧压接等刚性连接时,kj≫ki,i=1,2,3,即互连耦合刚度远大于结构刚度,模块间无相对位移,(x3-x1)≈0,该三自由度系统退化为图1形式的两自由度系统,但此时机壳的质量为m1+m3,刚度为k1+k3。

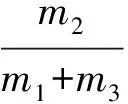
2 模态分析

2.1 理论分析

如图3所示,电子设备A主结构由机壳和印制板组件组成,印制板边缘分布一个QFP封装器件,电子设备A仅可实现某单一功能,当需要功能集成时,需与其他模块互连,构成如图4所示的电子设备B。

图3 电子设备A几何模型Fig.3 Geometric model of electronic equipment A

图4 电子设备B几何模型Fig.4 Geometric model of electronic equipment B

从结构连接关系可知,电子设备A可看作一个两自由度系统,而电子设备B则可看作一个互连耦合刚度较大的三自由度系统。基于上述隔振理论,可以估算电子设备A和电子设备B是否为解耦系统。

电子设备A:机壳质量m1=0.4kg,印制板组件质量m2=0.12 kg,质量比a=0.3,质量比属于“合理范围”,系统解耦。

电子设备B:机壳质量m1=0.4 kg,印制板组件质量m2=0.12 kg,其他模块质量m3=5.3 kg,质量比a=0.02,质量比不属于“合理范围”,若刚度比不合理,则系统不解耦。

下面可以通过有限元分析来验证电子设备A和电子设备B是否属于解耦系统。

2.2 有限元数值分析

图5 电子设备A固有频率Fig.5 Natural frequency of electronic equipment A

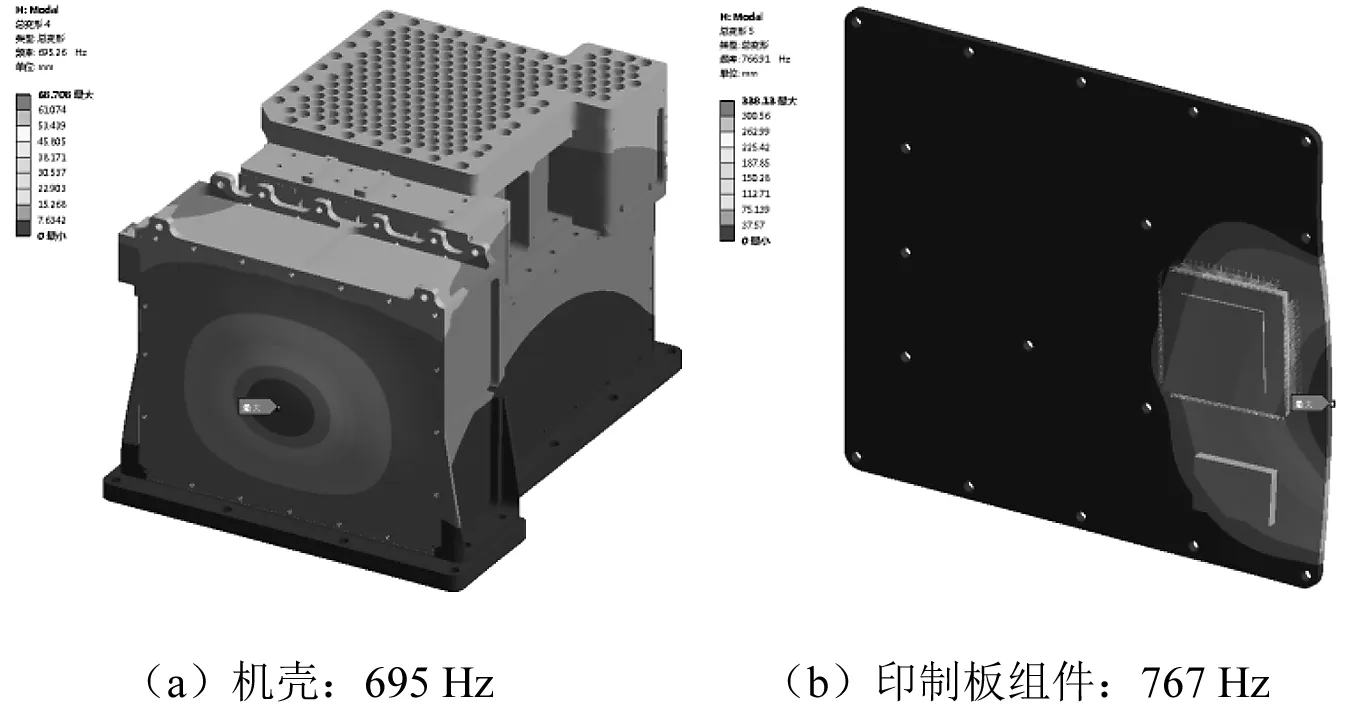
图6 电子设备B固有频率Fig.6 Natural frequency of electronic equipment B

3 响应分析

3.1 振动响应分析

动力学耦合是电子设备力学设计的最大禁忌,可能导致结构损伤、元器件损坏、设备性能异常等故障[11-13],当然电子设备的力学响应与环境载荷密切相关,因此对于上述的“解耦”、“耦合”系统,还需要通过进一步的力学响应分析,预示其是否安全、可靠,表1为随机振动输入条件。

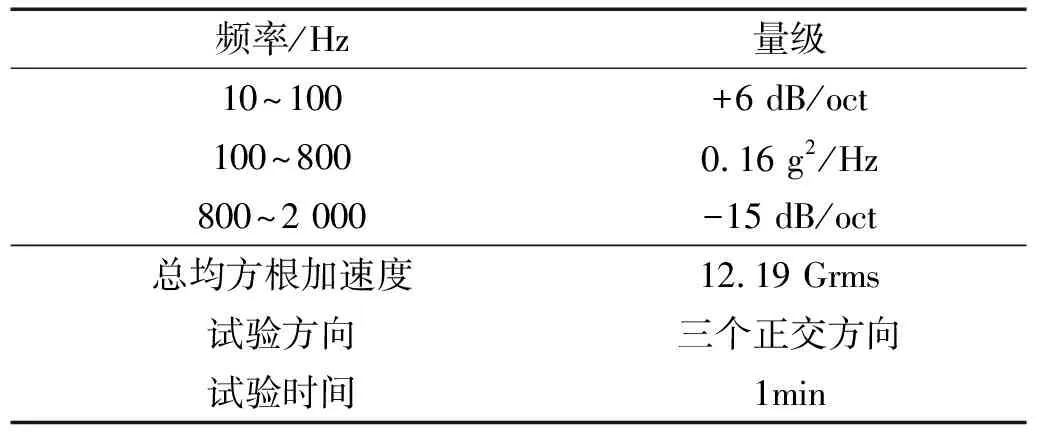
表1 随机振动输入条件

图7、图8分别为印制板法向随机振动载荷下电子设备A和电子设备B中QFP封装器件的引线应力云图,表2对比了印制板法向随机振动载荷下电子设备A和电子设备B的印制板组件翘曲变形、QFP加速度响应、QFP引线最大应力。从中可知, “解耦”产品(电子设备A)的力学响应(印制板组件翘曲变形量、QFP元器件加速度响应及引线应力)明显小于“耦合”产品(电子设备B)。

表2 电子设备A和电子设备B随机振动响应

图7 电子设备A器件引线应力云图(σmax=95.8 MPa)Fig.7 Stress contour of lead for QFP in electronic equipment A(σmax=95.8 MPa)

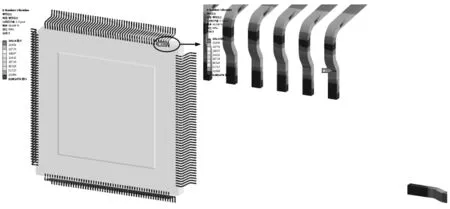
图8 电子设备B器件引线应力云图(σmax=241.4 MPa)Fig.8 Stress contour of lead for QFP in electronic equipment B(σmax=241.4 MPa)

基于强度理论,应力较大产品的失效概率大于应力较小的产品,换而言之,应力较大产品的工作寿命也小于应力较小的产品,因此需开展进一步的寿命分析,以确定产品是否可满足使用要求。

3.2 疲劳寿命分析

由于在前期设计阶段,已考虑到元器件可能发生力学失效,因此现代电子设备普遍对于质量较大、质心较高、支撑刚度较弱的元器件采取了加固措施,加固措施的使用已基本解决了元器件在各种力学工况下强度失效的问题,但由于设计不合理、力学工况恶劣等导致的元器件疲劳失效问题时有发生。

针对疲劳失效,需基于合理的失效物理模型开展定量分析工作。从工程应用角度考虑,安装于印制板上的电子元器件在振动载荷下的疲劳寿命可采用Palmgren-Miner累积损伤理论进行计算。

QFP封装器件的引线材料为可伐合金,其S-N曲线如图9所示。如果已知直线段1-2上某一点的应力水平,可由公式求得该应力水平下的疲劳寿命,即失效循环次数。

图9 Kovar疲劳寿命曲线(对数坐标)Fig.9 Fatigue curve of Kovar lead(log-log)

如果将曲线用数学公式表示,即

(10)

一个随机振动工况下的电子元器件引线或焊点的疲劳损伤为

(11)

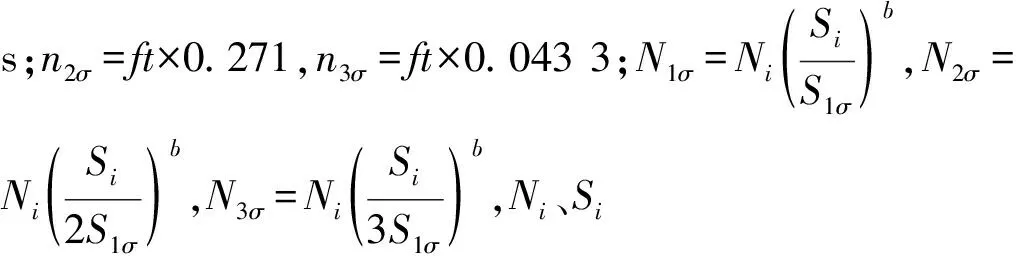
对于多个随机振动工况,则总的损伤

(12)

考虑到工艺加固后QFP封装器件的受力特性:印制板法向振动载荷下器件引线、焊点的应力远大于水平方向,因此在计算疲劳寿命、损伤因子时仅考虑印制板法向的随机振动工况可完全满足工程需要。表3列出了电子设备A和电子设备B中QFP器件引线在印制板法向随机振动载荷下不同应力水平的疲劳寿命及损伤因子。

表3 电子设备A和电子设备B疲劳寿命及损伤因子

根据Miner法则,当D<1时,材料不会发生疲劳破坏,而D≥1时,材料将发生疲劳破坏,但在工程实践中,由于各种因素的影响(如振动试验前的其他试验、计算误差、材料表面状态等),疲劳损伤因子不宜太大,由于航天航空行业的高可靠性需要,可以将疲劳损伤因子的阈值设定为小一个数量级,即D<0.1。

根据此准则,从3σ疲劳寿命和损伤因子可以看出,电子设备A中QFP器件可满足环境试验的要求(振动试验时间1 min,D<0.1),而电子设备B中的QFP器件在振动试验中将发生疲劳断裂,这从产品的振动试验中已得到验证。

如图10所示,左图为电子设备B中QFP器件焊接于印制板的状态,右图为力学试验后引线断裂而解焊的状态,可以看出该器件右上角的几个引线已断裂,且断裂位置与有限元仿真分析结果高度吻合。

图10 QFP器件随机振动疲劳失效图片Fig.10 The picture of fatigue fracture for QFP under random vibration

4 设计改进

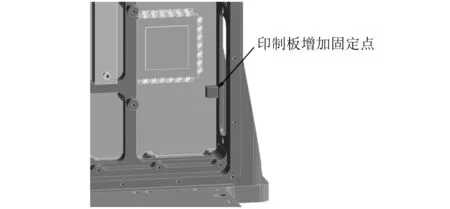
图11 电子设备B设计改进措施Fig.11 The improvement of electronic equipment B

图12给出了设计改进后电子设备B(改进后状态命名为“B+”)机壳及印制板组件的基频。图13给出了印制板法向随机振动载荷下器件引线的应力云图。表4列出了印制板法向随机振动载荷下改进后的分析结果。表5列出了印制板法向随机振动载荷下不同应力水平的疲劳寿命及损伤因子。将表4、表5与表2、表3对比,改进设计可实现机壳与印制板组件的动力学“解耦”,显著降低引线应力,减小疲劳损伤因子,提高疲劳寿命。

表4 电子设备B+随机振动响应

表5 电子设备B+疲劳寿命及损伤因子

图12 电子设备B+固有频率Fig.12 Natural frequency of electronic equipment B+

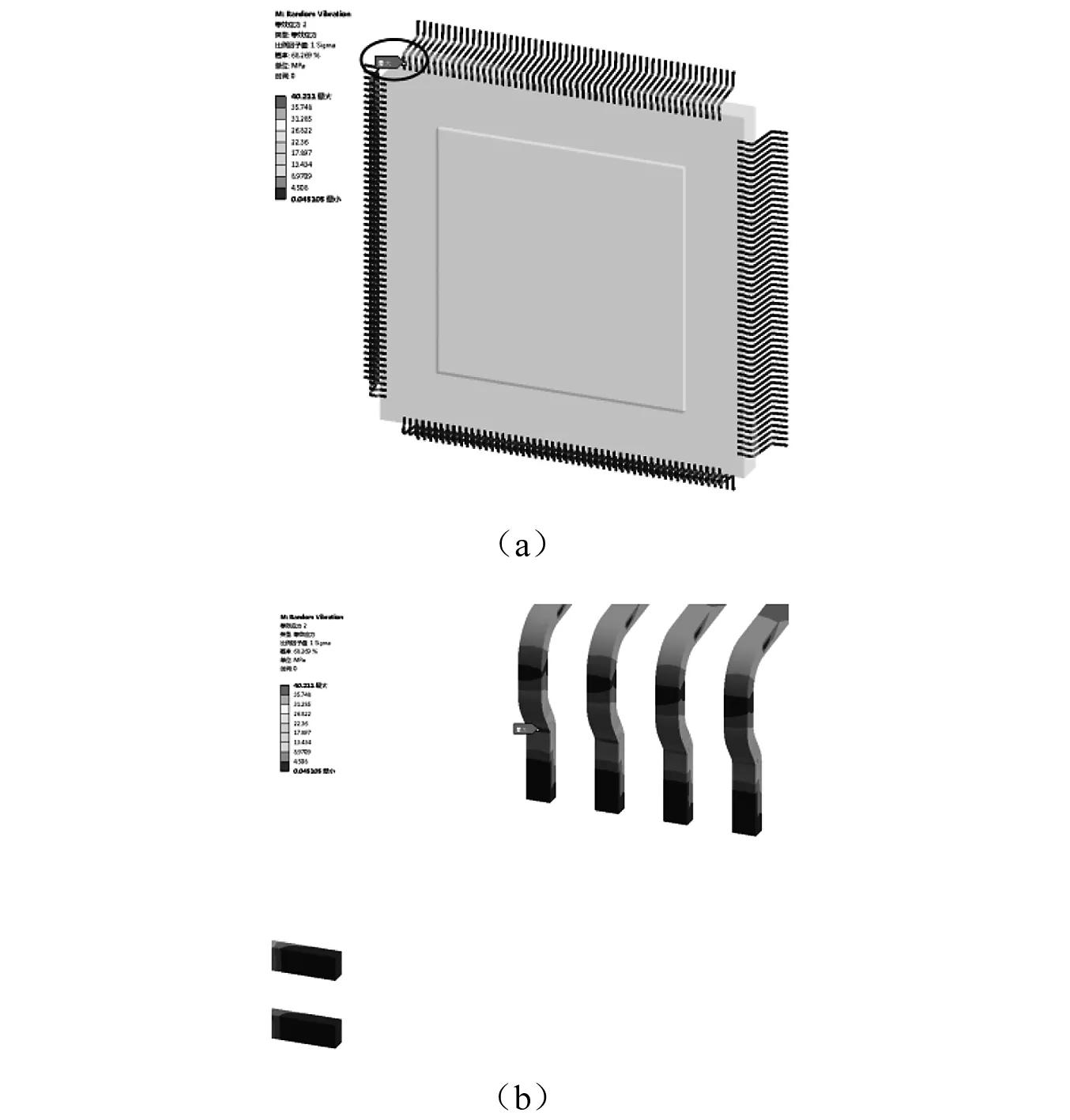
图13 电子设备B+器件引线应力云图(σmax=40.2 MPa)Fig.13 Stress contour of lead for QFP in electronic equipment B+(σmax=40.2 MPa)

前面的理论分析及数值仿真分析均预示了改进措施的有效性,但工程上的设计更改还需要开展验证试验。拆除引线断裂的QFP器件,在其焊装处粘贴加速度传感器,如图14所示,由于传感器的质量特性、刚度特性与QFP器件有明显的差异,因此该验证试验仅对比改进前后的加速度响应,以此间接说明更改的效果,而不是对有限元模型准确性的验证。

图14 加速度传感器位置Fig.14 Location of accelerometer

为避免大量级的力学试验对其他元器件产生损伤,验证试验的输入量级为正式试验的1/4,即总均方根加速度为3.05 Grms。图15给出了该验证试验的控制及响应曲线。其中:图15(a)、图15(b)的上图均为控制曲线;图15(a)的下图为原设计状态的加速度响应曲线,主方向总均方根加速度为62.88 Grms;图15(b)的下图为设计改进后的加速度响应曲线,主方向总均方根加速度为13.13 Grms。加速度响应大幅减小,放大率由20.6降低为4.3,表明增加印制板组件刚度的设计改进措施效果很好。按照设计改进措施对产品进行修复,随后顺利通过了振动试验的考核。

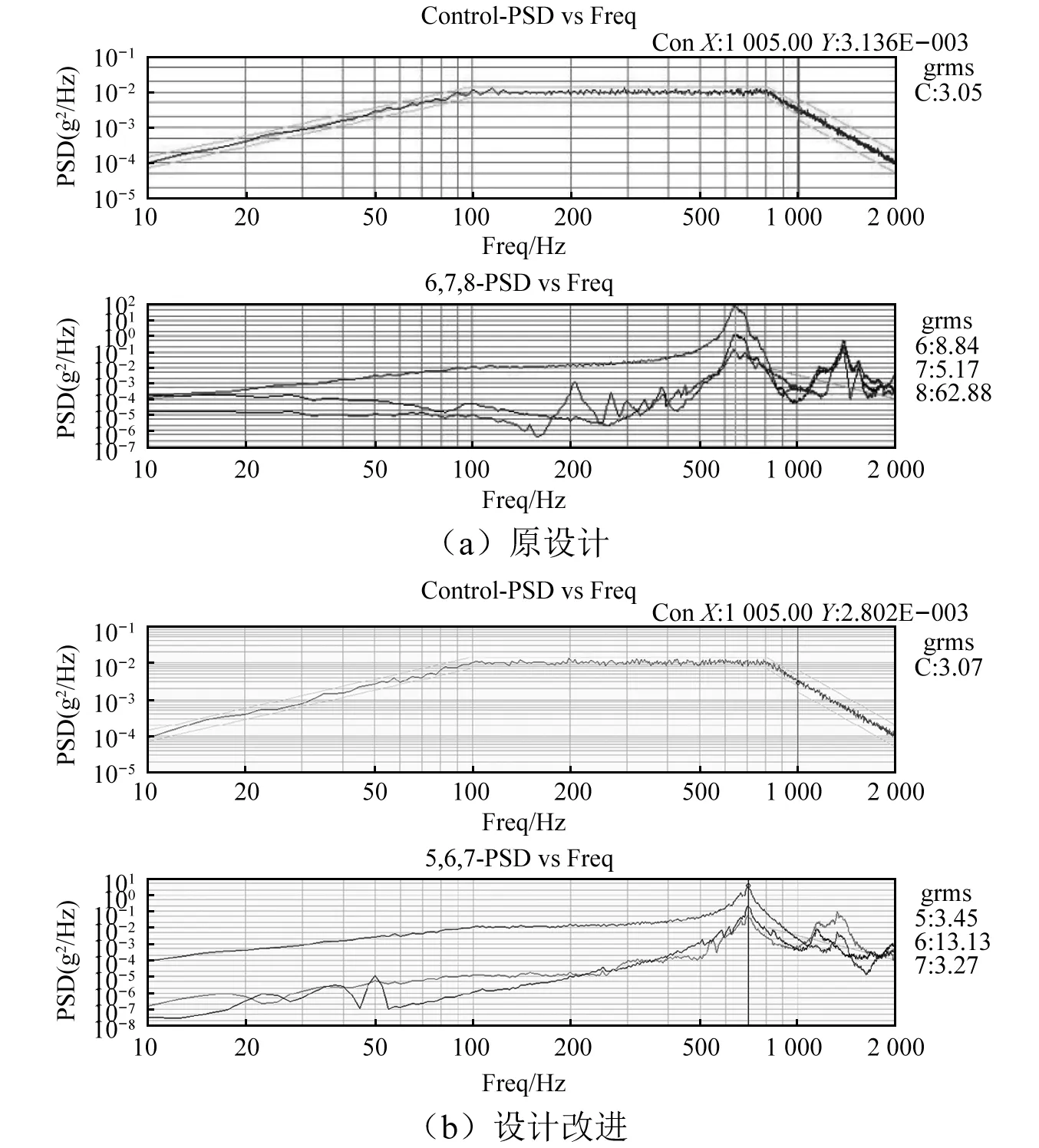
图15 验证试验曲线Fig.15 Curves of verification test

5 结论

现代电子设备功能的复杂特性决定了其模块化设计的必然,而模块间的结构互连将导致电子设备整机动力学特性的改变,当互连耦合刚度不合理时,电子设备机壳与印制板组件将发生共振,导致结构损伤、性能异常、器件断裂等灾难事故,因此在工程实践中,必须要重视互连耦合刚度的影响。

本文研究了电子设备互连耦合状态的隔振理论,针对某电子设备随机振动后QFP封装器件引线断裂的问题,应用该隔振理论开展了理论分析,并通过有限元仿真验证了理论的适用性,分析了试验环境下QFP器件的振动响应,计算了器件引线的疲劳寿命,最后基于隔振理论提出了改进措施,保证了电子设备的力学可靠性。对于电子设备内部模块间的互连耦合,有如下结论:

(1)当电子设备模块间为柔性互连时,互连耦合刚度对各模块的动力学特性影响很小,各模块仅需要满足各自机壳与印制板组件的“解耦”条件,即可保证动力学特性设计的合理性。

(2)当电子设备模块间为刚性互连时,互连耦合刚度对各模块的动力学特性影响较大,各模块需考虑因互连其他模块导致的动力学特性变化,调整其质量特性、刚度特性或连接刚度,以满足“解耦”条件,确保其动力学特性合理、可靠。