激振法对软岩高地应力超前释放数值模拟研究

朱 英, 李新宇, 尤卫星, 唐小微

(1. 中铁工程装备集团有限公司,郑州 450016;2. 大连理工大学 海岸和近海工程国家重点实验室,辽宁 大连 116024)

二十一世纪已经步入了发展隧道与城市地下空间工程的时代[1],隧道在交通网络建设当中已经具有了举足轻重的地位,但随着隧道的开挖深度与长度在不断的增加,所面临的施工地址条件也随之变得越来越复杂,给实际建设会造成一系列的问题,高地应力软岩大变形就是其中之一[2]。软岩大变形问题一般出现在变质岩、破碎断层、煤系地层等低强度围岩中[3],变形速率达到0.1～5 m/min,围岩快速收敛过程中将导致混凝土管片的变形和破损,阻碍隧道掘进机(tunnel boring machine,TBM)的正常掘进,严重时甚至发生卡机现象,增加了设备的故障机率[4]。从破坏形式和形成机理方面来划分,大变形的形成机制主要分为两种[5-7]:一是塑性挤压大变形,主要是由于开挖后围岩应力在高地应力的基础上重分布后使强度高于软岩的自身强度;二是岩体体积膨胀大变形,主要是由于矿物与水发生反应后膨胀造成。综合上述两种变形机理,在隧道施工围岩变形问题中,挤出和膨胀共存,但单纯的膨胀引起的大变形比较少见,而塑性挤压大变形是引发隧道围岩大变形的主要机制[8],因此在实际工程当中,会采用各种手段避免由于高地应力所产生的危害。

国内外学者针对高地应力进行了大量的研究并且以及取得了丰硕的成果,目前应对高地应力的手段主要分为两个方向:一个方向是在开挖过程当中进行预处理,从而完成对应力的卸载,包括钻孔卸压、爆破卸压、水压至裂等;另一个方向则是通过改进开挖方式和后续支护结构,来完成对高应力的抵抗。

陈荣华等[9]针对高地应力地质条件复杂的矿场顶板塌落问题,通过预先注水软化的方式对关键岩层进行预处理,并且通过RFPA2D软件验证了软化系数和软化厚度不同对于预防效果的影响。王伟[10]分析了在造穴作用下,煤体围岩的应力以及塑性区分布机理,结合水流的冲击特性与聚能效应,通过高压水流射入冲孔的方式完成卸压。闫鑫[11]将煤炭领域的超前导洞应力释放技术引入到铁路隧道当中,完成了超前导洞应力释放技术在铁路隧道当中应用的可行性。Zang等[12]分析了煤矿巷道围岩分别在静荷载以及不同扰动强度下的动荷载作用下的变形结果、应力场变化以及塑性区分布,并进行了喷锚与钢筋锚索联合支护方案的优化改良。Duan等[13]采用数值模拟与现场观测结合的方式,分析了爆破前后衬砌、围岩、锚杆以及围岩的稳定性,对爆破扰动后的围岩安全性进行了系统的评估。杨英明[14]研究了开拓巷道前煤层应力场分布规律,并模拟了岩层在进行超前钻孔卸压情况,证明了超前钻孔增强了卸压区的范围同时降低了瓦斯突出风险。Aliev等[15]研究了开拓巷道前煤层应力场分布规律,并对岩层在进行钻孔卸压情况下的应力应变状态进行了数值模拟,增强了卸压区的范围同时降低了瓦斯突出风险。魏明尧等[16]运用FLAC3D软件进行数值模拟,分析了不同条件下钻孔卸压爆破前后的围岩应力分布和转移规律,探究了装药量、煤层厚度对爆破卸压效果的影响。

但以上方法都存在一定程度的问题,改进开挖方式以及支护等方法存在滞后性,但在实际工程当中有相当多的变形问题集中发生在开挖之后的较短时间,这段时间内发生的变形会拖延正常的施工进度。因此针对实际工程,提出一种利用激振器进行冲击振动的方式,引发共振效果来提前释放隧道高地应力,采用机械激振的方式相比于爆破方式有效提高了施工的安全性以及效率,相比于水压致裂等超前方式降低了整体设备的体积以及施工的便捷性。下文将针对TBM掘进后通过打入小导洞进行超前激振的方式,来验证激振法卸除高地应力的可行性。

1 激振器具结构及作用原理

目前激振器主要分为金属振动时效激振器,试验台用激振器。激振器是附加在某些机械或者上背上用于产生激振力的设备,其原理是将电能转换为机械能,依据激振起动方式的区别主要分为机械式激振器、液压式激振器、电磁式激振器、电动式激振器四种。除此之外还有液压夯实机和可控震源系统可以提供激振力。但液压夯实机与可控震源系统虽然可输出的力较大,但频率较低且体积过于巨大、设备过于沉重,因此针对实际小导洞激振方式,采用金属振动时效激振器和试验台用激振器作为实际激振源,并综合TBM系统,将激震系统与TBM系统集成为一体,研制出新型设备,完成掘进与激振设备的一体化。使得TBM在遇到软岩地区时,可以进行激振预处理,对掌子面前方一定范围内的应力进行释放,从而有效降低了变形量,减小TBM机在围岩变形后卡机的风险。

本设备如图1所示包括TBM系统与激振系统两部分组成,TBM系统以中心处设有孔洞的刀盘为主,激震系统则包括:推进梁、推进油缸、钻杆、激振设备。整体过程为刀盘在掘进过程当中遇到软岩地区,停止掘进,从中心孔洞处启动推进油杆进行导洞的钻进,在钻进到合适的深度之后,再采用激振器进行振动,从而在一定范围内完成对应力的释放,振动预定的时间之后,再次启动推进油缸将钻杆与激振器收回并拆卸,之后重新启动TBM进行掘进,掘进一定进深之后再次进行以上的操作,重复数次完成对软岩地段的开挖,从而达到对于高地应力的超前释放,降低管片后续变形以及卡机事故出现的几率。

图1 适配TBM小导洞激振设备图Fig.1 TBM small hole vibration equipment

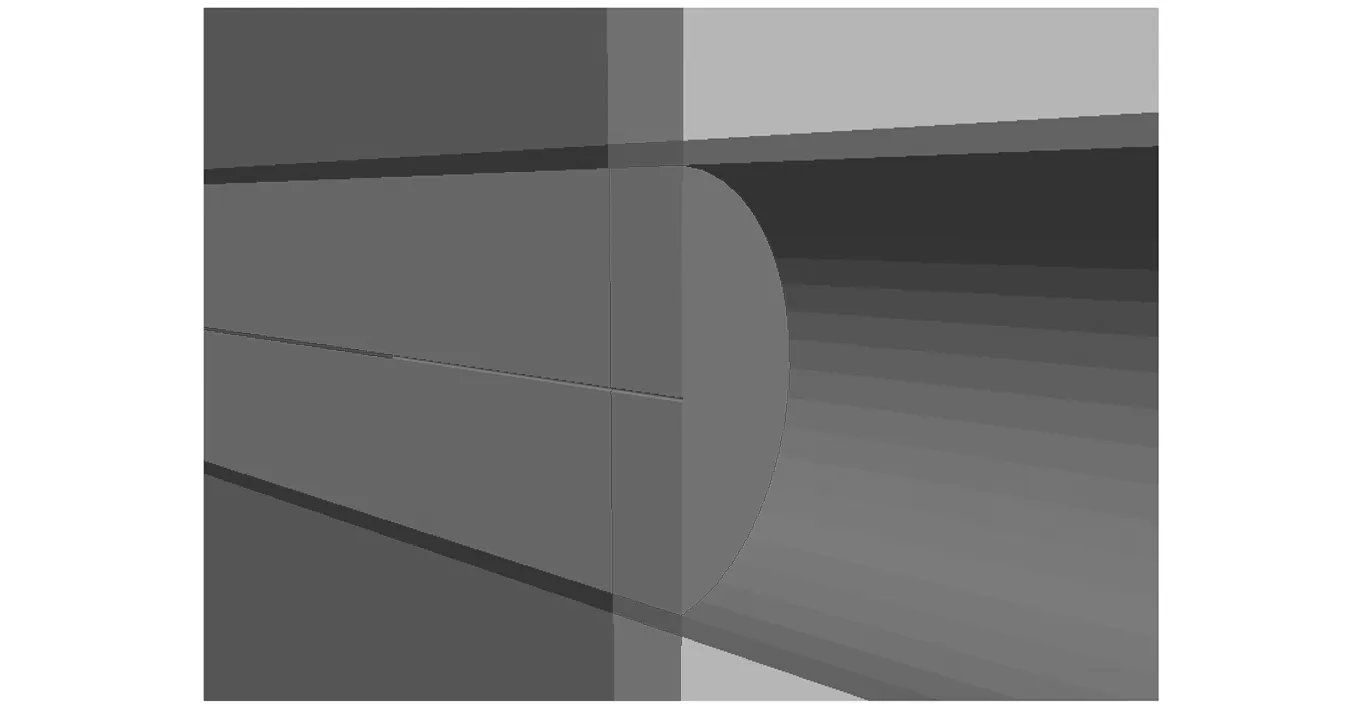
图2 隧道模型Fig.2 Tunnel model

2 数值模拟

2.1 建立模型

针对上述TBM小导洞模型进行建模,本文采用FLAC3D有限差分软件进行模拟,对TBM小导洞掘进模型进行计算,模型整体为立方体,长宽高均为90 m,掌子面直径为10 m,在掘进掌子面中心处开挖直径0.1 m小导洞,深度为10 m,模型上部压力为10 MPa,围压为5 MPa,荷载加载方式为在导洞的左右两侧进行施加相差半个周期的正弦变化式荷载,模型底部采用固定位移边界,施加三向位移约束,四周采用黏性边界对振动能量进行吸收,模拟无限大边界条件,顶部采用自由边界。岩土体本构选择摩尔库伦本构进行模拟并为岩体赋予参数,如表1所示。

表1 岩土体参数Tab.1 Parameter of rock

2.2 寻找共振频率并研究频率对于整体结果影响

针对岩石体,选择开尔文体作为岩石的振动模型,该模型是一种典型的、具有一定代表性的岩石力学组合模型,也是岩石动力学的基本模型。开尔文体的组合模型如图3所示。

图3 开尔文本构模型Fig.3 Kelvin model

加载的谐振激励符合正弦变化规律,振动方程为

(1)

式中:m为质量,kg;C为阻尼系数,Ns/m;X为振动位移,m;t为时间,s;k为刚度,N/m;F为谐振冲击力;ω为谐振冲击力频率, Hz;A为谐振冲击力振幅,m。

(2)

式中,a为位移响应振幅。

(3)

(4)

式中,ω0为岩石的固有频率。

由公式可知,当冲击力频率接近共振频率时,位移响应振幅最大,响应最强,同时响应的范围最广。

激振频率从1～2 000 Hz取若干工况进行激振模拟,通过与初始应力状态对比,可以得到如图4所示的在激振完毕后有效的应力释放范围随频率变化曲线,通过曲线我们明显可以发现一个十分突出的波峰,因此我们认为在此频率下,产生了共振现象。当频率小于共振频率时,应力释放范围随频率升高而增大,在达到共振频率100 Hz左右,应力释放范围达到峰值,后续当频率继续的增大,远离共振频率之后,激振所影响的范围明显减小。

图4 应力释放深度范围Fig.4 Stress relief range

在激振后,进行隧道的开挖并对隧道衬砌顶部选择若干测点进行沉降量数据进行检测,得到如图5所示沉降曲线。横轴对标为隧道的进尺,纵轴坐标为隧道沉降量。

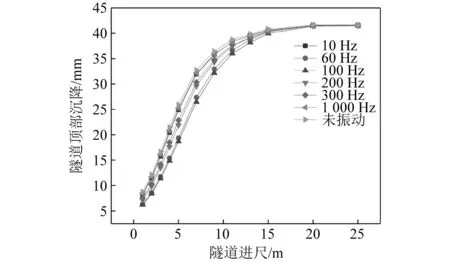
图5 后续开挖隧道沉降曲线Fig.5 Tunnel excavation settlement curve

由图5可知,我们可以确定激震法可以完成应力超前的释放和降低后续隧道开挖的沉降变形且在100 Hz频率工况下隧道沉降最小,在隧道进尺5 m处,对比未振动工况沉降量有效降低了28%。因此针对本工况,在100 Hz共振频率下对于隧道的超前应力释放效果最优。在实际施工过程当中我们认为相较于其余振动频率,共振频率对于改善隧道沉降效果更好,共振能够有效地促进应力的释放,故应当在施工过程当中将激振频率尽量贴近实际共振频率,以达到最优应力释放效果。

2.3 振幅对于整体卸荷效果的影响

在得到最优频率即共振频率之后,继续针对振动幅值进行了多工况模拟以期望得到激振法的最优激振幅值。

图6为应力释放范围随振动幅值变化曲线,我们在0.1～5 GPa合理选择若干工况来进行了激振分析。可以发现在激振幅值达到2 GPa之前,应力释放范围是随着幅值增大而不断增大,应力释放范围在2 GPa时达到峰值,后续略有降低,但整体降低幅度较小。为了进一步探究最优激振幅值,在激振完毕之后进行隧道的开挖模拟,开挖方式与2.2节相同相同,对后续隧道开挖以及衬砌施作采用一次开挖成型的方式。

图6 应力释放深度范围Fig.6 Stress relief range

图7为不同激振幅值下隧道沉降量监测曲线。可以明显观察到当振动幅值达到在2 GPa后,隧道沉降量最小,在隧道进尺7 m处,沉降量相比未振动工况降低了45%。继续增大振动幅值后,对隧道沉降的改善效果在10 m之前略低于2 GPa,在10 m之后又小幅度的提升,超过2 GPa这一振幅阈值之后,后续加大振幅所得到的效果不明显,相对于能量的额外增加,所得收益不成比例。对于实际施工当中,应选择性价比更高的激振施加方式,同时考虑到预期的激振施工方式为在软岩段不断重复激振—开挖—再激振的模式,因此我们认为2 GPa这一激振幅值为针对本工况的最优振幅。

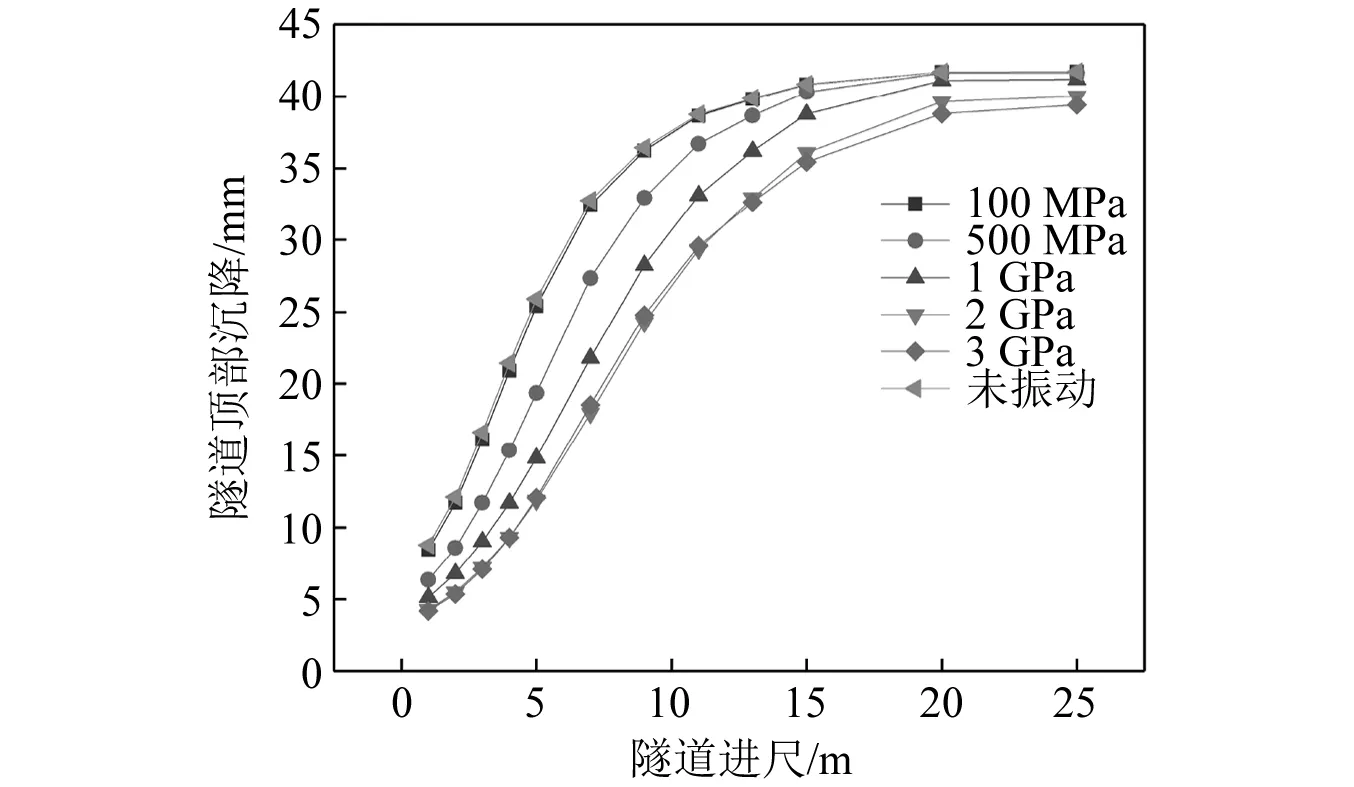
图7 后续开挖隧道沉降曲线Fig.7 Tunnel excavation settlement curve

2.4 激振深度对整体协和效果的影响

在分别对于激振频率以及激振幅值进行一定程度研究后,针对探究深度进行研究。多次改变激振点的深度,从深6 m开始,每加深2 m进行一次激振模拟直到深度达到16 m为止,得到如图8所示各工况下竖向应力分布云图并将各工况有效应力释放范围数据进行汇总,如表2所示。

表2 不同激振点深度工况下应力释放范围Tab.2 Stress relief range in different vibrate position 单位:m

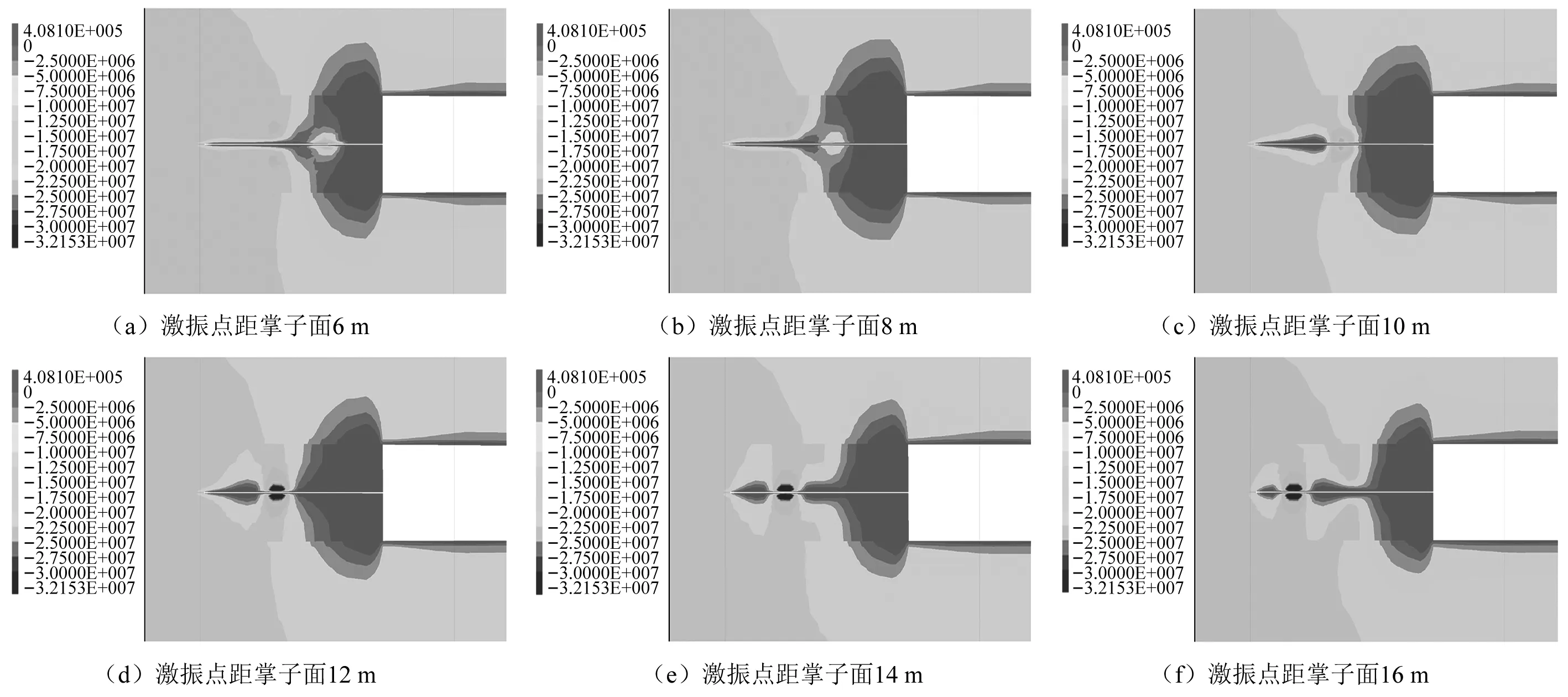
图8 不同激振点深度工况下竖向应力云图Fig.8 Vertical stress in different vibrate position

图8为不同激振深度下的竖向应力云图,展示了不同深度工况下的应力释放效果,维持激振频率为100 Hz,激振幅值为2 GPa,可以明显观察到当激振点深度为8 m时,应力释放范围最大,当激振点距离掌子面超过10 m之后,应力释放范围逐渐减小,同时激振点附近位置产生比较明显应力集中现象。综合分析原因为当激振点距离掌子面过近时,由于靠近掌子面部分已经由于开挖所导致部分应力释放,所以激振效果不明显;当激振点距掌子面过远,受扰动岩体无法依靠自由凌空面的空间进行应变,从而无法完成整个应力释放过程,在激振点处产生应力集中的现象。

图9为距离掌子面6～16 m不同工况下的激振后隧道开挖沉降曲线,进一步证明上述的总结:8～10 m的激振深度下,应力释放的效果最优秀,过大以及过小的激振深度,都不利于掌子面处的应力释放,过小的激振深度会导致激振影响区与开挖所导致的应力释放区重叠,使得激振应力释放效果不明显;过大的激振深度会使得激振影响区与掌子凌空面距离过远,无法充分的释放影响区的应力,从而减少后续的开挖变形。

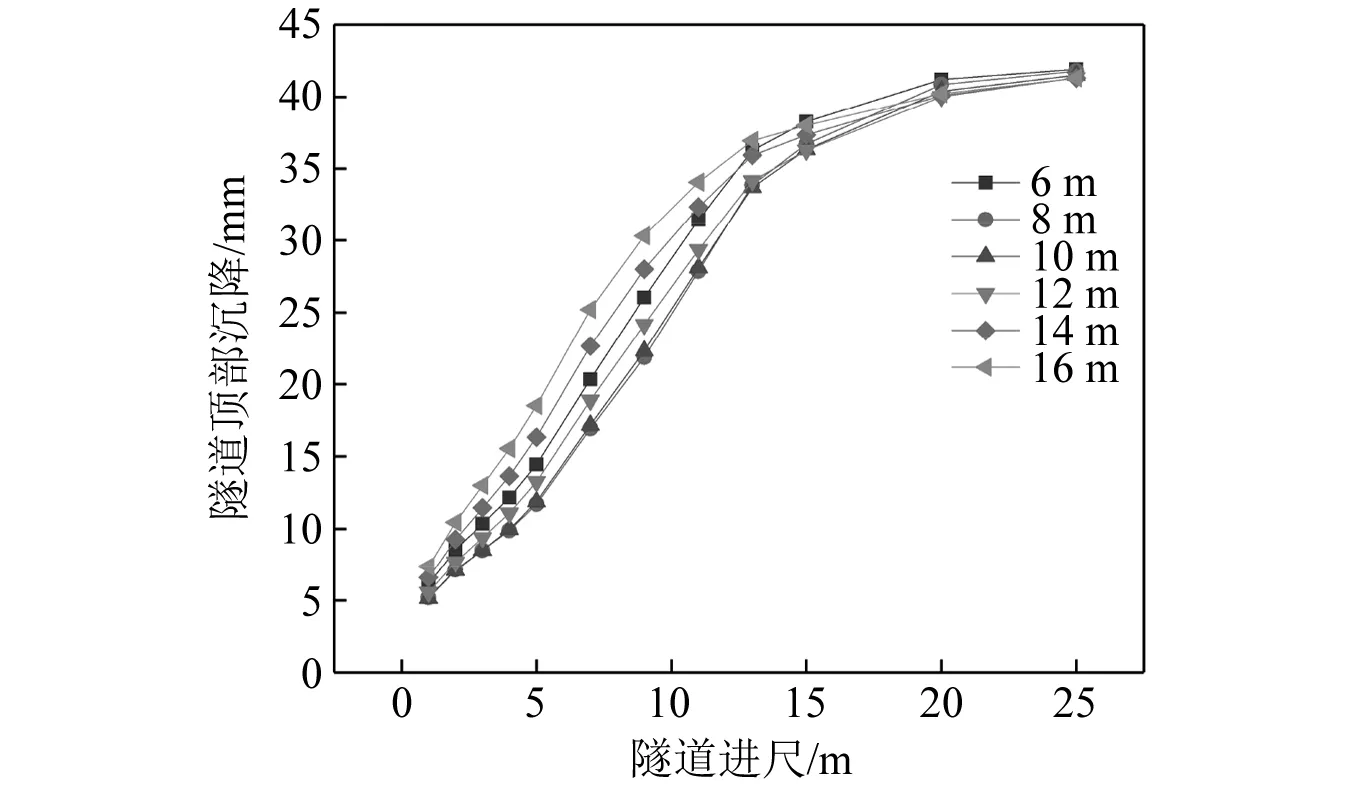
图9 后续开挖隧道沉降曲线Fig.9 Tunnel excavation settlement curve

2.5 最优激振结果组合

综合上述结果,选择8 m的激振深度、2 GPa的激振幅值以及100 Hz的振动频率做为最优激振方式,并以此方式来对TBM小导洞模型进行激振处理,从而得到如图10所示的隧道沉降曲线,通过对比未经过激振处理以及激振后的隧道沉降曲线,发现隧道沉降情况有了明显的改善,证明机械激振法可以完成应力的超前释放,对于隧道后续的开挖是有益的,可以显著的降低隧道的变形,防止TBM卡机等事故的发生。同时可以发现机械激振的处理效果范围有限,不能做到一劳永逸,所以在实际施工过程当中,应考虑采取激振处理开挖一段距离再进行激振的循环施工操作,采取此种操作通过软岩区之后再恢复为正常TBM掘进施工进度。

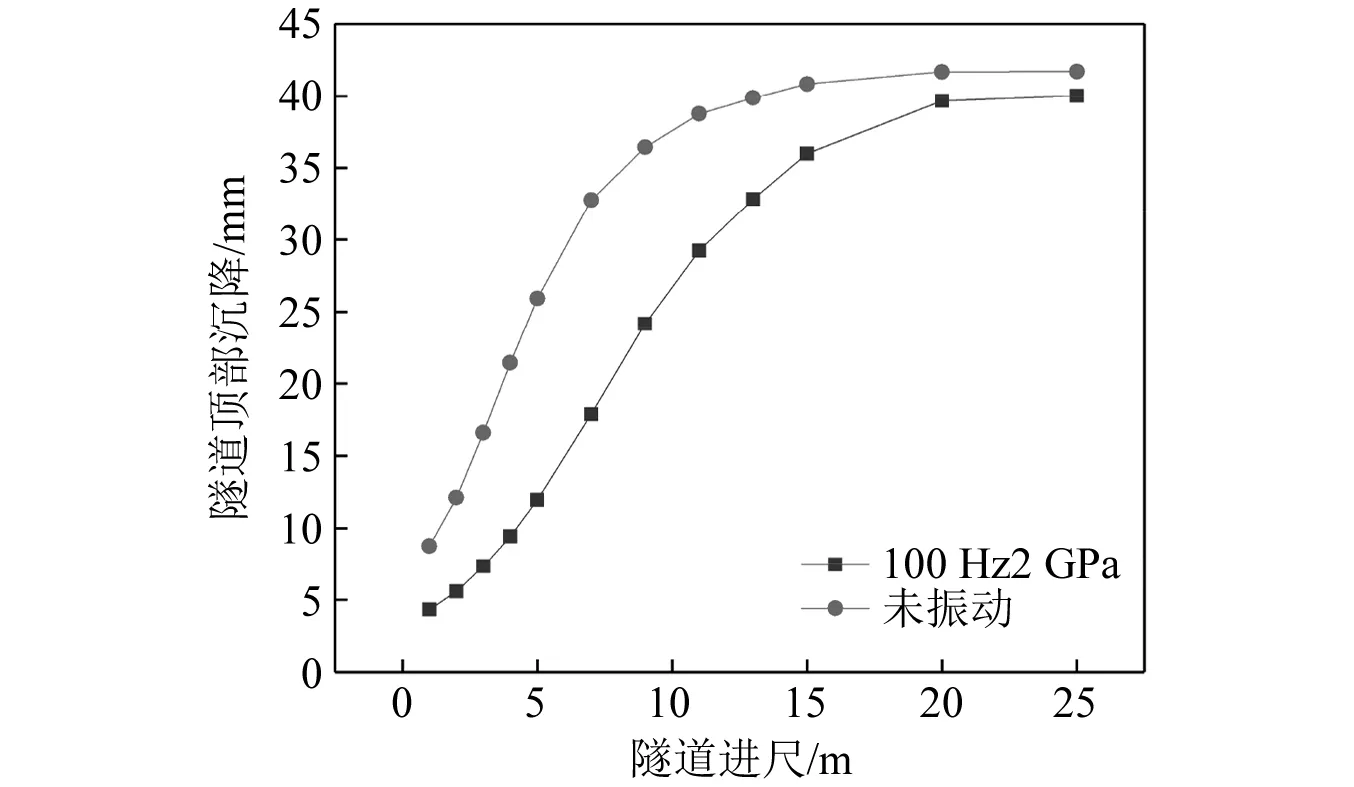
图10 最优组合隧道沉降曲线Fig.10 Tunnel settlement curves of optimum combination

3 结 论

本文采用FLAC3D软件,根据目前应力释放现状针提出一种新的超前应力释放方法,并基于一种依托TBM的综合激振设备,进行数值模拟研究,研究了频率、振幅以及激振深度三方面因素对于应力释放效果的影响,并依据数值模拟结果总结了合理的激振频率、幅值,其结果为:

(1) 首先针对模型在不同频率下的响应,确定其共振频率,将不同频率下激振后的应力释放深度范围以及后续隧道开挖沉降的结果绘制成图,发现在共振频率下相对于未振动工况隧道沉降量降低了28%,同时共振频率下的隧道变形也明显小于其他频率,证明在共振频率的优越性,初步证明方法可行性,并且针对实际施工当中应将激振频率尽可能的贴近实际集镇频率,以此达到应力释放的最优效果。

(2) 在共振频率的基础上改变激振幅值,通过数值模拟结果发现增大幅值一定程度上有利于应力释放效果的提升,但幅值存在提升的阈值。在本模型当中,当超过2 GPa这一阈值之后,后续继续加大振幅所得到的释放效果提升不明显,相比于能量的额外增加,所得到的收益不成比例,因此针对本方法确定了2 GPa为本次模拟合理的激振幅值。

(3) 针对激振深度进行大范围的改变并观察不同深度对于激振效果的影响,可以发现当采用8 m激振深度时,应力释放范围最大可以提升30%。因此针对此模型选取8 m作为合适的深度,过大或者过小都不利于应力的释放,导致应力释放范围的降低。当激振位置过浅会使得激振应力释放区与由于开挖导致的应力释放区重叠,造成能量的浪费;当采取过深的激振位置时,激振点与掌子面中间的未扰动岩体会使得深处受到扰动的部位无有效的凌空面释放应力。故激振点位置需选择较合适位置,针对实际工程当中需要结合现场情况进行合理选择。