S空位与Tc掺杂单层MoS2的电子结构和磁学性质模拟

付斯年,朱瑞华

(牡丹江师范学院物理与电子工程学院,牡丹江 157011)

0 引 言

稀磁半导体 (diluted magnetic semiconductor, DMS)因兼具电荷和自旋的属性而引起人们广泛关注[1],其中MoS2结合了光学、电子和磁学特性,是一种非常有潜力的稀磁半导体,在自旋电子器件中得到广泛研究[2]。块体MoS2是间接带隙半导体,禁带宽度为1.29 eV[3]。由于具有较窄的禁带宽度和缺乏光致发光行为,块体MoS2在自旋电子应用方面存在局限性。单层MoS2(ML-MoS2)作为新兴的二维材料,因具有不同于块体MoS2的物理和化学性质而引起了科学界的广泛关注[4-5]。ML-MoS2是一种直接带隙半导体,禁带宽度为1.80 eV[6]。然而与块体MoS2相同,ML-MoS2也是非磁性材料。因此,实现和调节 ML-MoS2的磁学性质已成为快速开发MoS2基自旋电子元件的关键[7-8]。

目前,关于ML-MoS2中空位和掺杂剂的研究已通过理论和实验方法广泛开展。理论上,Yun 等[9]研究了3d过渡金属掺杂的ML-MoS2,计算表明V、Mn、Fe、Co、Ni 的掺杂可使体系具有磁性。Pan等[10]利用第一性原理计算研究了Tc掺杂MoS2纳米带的电子结构。实验上,Xia等[11]制备了Cu掺杂的ML-MoS2纳米片,证明了饱和磁化强度随着Cu浓度的增加而增加。目前,掺杂与引入缺陷依然是调节半导体性能的有效手段。4d过渡金属原子具有较多的未饱和d轨道,掺杂后会使半导体的能带结构及磁学性质发生改变。4d过渡金属Tc 掺杂与S空位对ML-MoS2电子结构的影响较少被关注。因此,本文对Tc 掺杂与S空位对ML-MoS2电子结构的影响进行模拟计算,以期为MoS2基的自旋电子器件应用提供理论指导。

1 模拟方法

1.1 计算方法

基于密度泛函理论,使用平面波超软赝势法进行几何优化和电子结构计算,并在 CASTEP模块中实现运算。根据 PBE (perdew-burke-eruzerhof)方案的广义梯度近似描述电子交换能[12]。文中所选价电子组态分别为 S-3s23p4、Mo-4d55s1、Tc-4d55s2。计算中,选择平面波截止能量为480 eV,能量计算的收敛精度为1.0×10-5eV/atom,布里渊区的采样网格选取为6×6×1。所有原子完全弛豫,作用在每个原子上的力小于0.5 eV/nm,应力偏差小于0.05 GPa。

1.2 理论模型

本文计算模型选取2H态MoS2,并建立了4×4×1超晶胞,用于各种掺杂系统。图1为单层MoS2原子结构模型。由图1可知,Mo原子被 Tc 原子取代的位点分别标记为 0～5,VS表示S空位。同时,沿原子层变化的方向创建1.5 nm厚的真空层。在几何优化的基础上,研究各种掺杂体系的电学及磁学性质,并且所有计算均使用自旋极化进行。为了探索不同构型的稳定性,引入了形成能Ef计算公式,具体如式(1)所示。

图1 单层MoS2原子结构模型Fig.1 Atomic structure model of monolayer MoS2

Ef=Edoping-Epure-nETc+mEMo+ES

(1)

式中:Edoping和Epure分别为掺杂体系和纯ML-MoS2的总能量,ETc、EMo、ES分别为Tc、Mo、S的化学势,n为Tc原子数,m为Mo原子数。

2 结果与讨论

2.1 体系磁性与态密度分析

图2为ML-MoS2、VS掺杂ML-MoS2、Tc掺杂ML-MoS2、(Tc,VS)掺杂ML-MoS2和2Tc(2个Tc原子)掺杂ML-MoS2的态密度和分波态密度(PDOS)。在研究各种掺杂模型的电子结构和磁性之前,本文计算了纯ML-MoS2体系的总态密度(TDOS),并将费米能级设置为0 eV。如图2(a)所示,纯ML-MoS2的自旋态密度呈对称分布,表明该体系是非磁性的,计算所得禁带宽度为1.772 eV,与实验值接近[6]。此外,本文还计算了VS掺杂ML-MoS2体系的总态密度。由图2(a)可知,VS掺杂ML-MoS2体系的TDOS曲线呈对称分布,这说明VS单掺杂无法诱导出体系的磁矩。另外,VS的存在相当于引入了电离施主,因此与纯ML-MoS2体系相比,VS掺杂ML-MoS2体系的带隙变小。

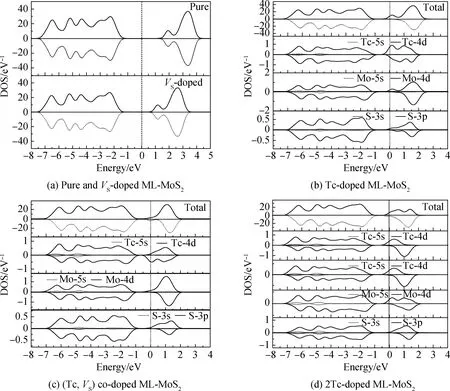
图2 ML-MoS2、VS掺杂ML-MoS2、Tc掺杂ML-MoS2、(Tc, VS)掺杂ML-MoS2和2Tc掺杂ML-MoS2的态密度Fig.2 Densities of states of ML-MoS2, VS-doped ML-MoS2, Tc-doped ML-MoS2, (Tc, VS) co-doped ML-MoS2 and 2Tc-doped ML-MoS2

首先研究Tc掺杂ML-MoS2体系的电学及磁学性质。在Tc掺杂ML-MoS2体系中,Tc—S键长为0.240 4 nm,与Mo—S键长(0.240 0 nm)非常接近,没有明显的晶格畸变,这可以归因于 Tc 的原子半径几乎与 Mo 原子半径相同。从图2(b)可看出,Tc掺杂ML-MoS2体系的TDOS不对称性很明显,说明该体系呈现出明显的磁性特征。并且在Tc-4d电子态诱导极化作用下,由于轨道杂化作用,Mo-4d和S-3p电子态密度分布产生了明显的非对称性,从而使体系产生了磁矩,该体系磁矩主要由Tc-4d、Mo-4d和S-3p电子态所贡献。考虑到Tc-4d55s2和Mo-4d55s1的价电子组态,Tc的替位掺杂可被看作是n型掺杂。这一点在图2(b)中也可得到证明,该体系的导带底位于-0.5～0 eV。经计算,Tc掺杂ML-MoS2体系的总磁矩为1.068 μB。

在(Tc,VS)掺杂ML-MoS2体系中(见图1),VS被固定在S原子的最顶层,并且在标记的位置(1～5)处,Mo原子被Tc原子取代。(Tc,VS) 掺杂ML-MoS2体系中5种不同构形的计算结果如表1所示。在表1中,使用符号(Tcx,VS)来标注不同的构型,其中x代表Tc原子的位置,Ef代表构型的形成能,并且这些值都是正的,这意味着共掺杂体系需要吸收更多的能量来实现5种构型。从表1可以看出,(Tc2,VS)构型具有最小的形成能,因而在5种结构中是最稳定的,这可能是由于当Tc-VS距离最小时,VS部分缓解了Tc掺杂引起的晶格畸变。基于以上分析,本文将重点讨论(Tc2,VS)构型。图2(c)为(Tc,VS)掺杂ML-MoS2体系的分波态密度曲线。从图2(c)中可看出,导带主要由Tc-4d、Mo-4d和S-3p态组成,并且在-8～-1 eV,TDOS主要由Tc-4d、Mo-4d和S-3p态贡献。如图2(c)所示,(Tc,VS) 掺杂ML-MoS2体系的TDOS是不对称的,说明该体系表现出铁磁特征。如表1所示,共掺杂体系的磁矩约为1 μB,Tc原子的磁矩为0.704 μB。与Tc掺杂ML-MoS2体系相比,VS的引入并没有导致(Tc,VS)掺杂ML-MoS2体系的总磁矩显著变化,且掺杂体系磁矩主要由Tc原子贡献。

表1 (Tc, VS) 掺杂ML-MoS2中5种不同构形的计算结果Table 1 Calculation results of 5 configurations for (Tc, VS) co-doped ML-MoS2

为了分析耦合相互作用导致的长程磁序,本文研究了2Tc掺杂ML-MoS2体系的磁矩。在该体系中,两个Mo原子分别被两个Tc原子替代。如图1所示,其中一个Tc原子被固定在0位置,另一个Tc原子的位置分别为1～5。在2Tc掺杂ML-MoS2体系中的5种不同构型的计算结果如表2所示。在所有构型中,(0, 4)构型的形成能Ef最低,说明(0, 4)构型最稳定。在表2中,ΔE代表铁磁态(FM)和反铁磁态(AFM)的能量差,ΔE的负(正)值意味着 FM(AFM)基态更稳定。如表2所示,(0, 4) 构型的ΔE为负值,说明该体系是FM。经计算,两个Tc原子的磁矩均为0.603 μB,且2Tc掺杂ML-MoS2体系的总磁矩为2.048 μB。

表2 在2Tc掺杂ML-MoS2中的5种不同构形的计算结果Table 2 Calculation results of 5 different configurations in 2Tc-doped ML-MoS2

对于2Tc掺杂ML-MoS2体系,本文计算了(0, 4)构型的PDOS,如图2(d)所示。从图2(d)中可以看出,Tc-4d 态的PDOS曲线具有不对称性,并且电子态密度分布呈现出明显的局域性特征,这意味着自旋极化出现在Tc原子周围。从图2(d)可以看出,TDOS 主要由 Tc-4d、Mo-4d 和 S-3p电子态贡献,而Tc-5s、Mo-5s和 S-3s电子态贡献较小。

2.2 自旋电子密度分析

图3为2Tc掺杂ML-MoS2体系中的自旋电荷密度分布,其中等值面设置为30 e/Å3。在图3中,蓝色区域由相同自旋电荷密度的点组成,主要分布在Tc原子周围,这意味着2Tc掺杂ML-MoS2体系的磁矩主要由Tc原子贡献,这一结论与前面的磁矩计算结果是一致的。两个Tc原子之间的最近Mo原子对磁矩耦合具有重要的调制作用。如图3所示,在2Tc掺杂ML-MoS2体系中,(Tc-4d)-(S-3p)-(Mo-4d)-(S-3p)-(Tc-4d)耦合链可能是2个Tc原子发生铁磁耦合的原因。该现象可用Zener双交换理论解释,铁磁耦合过程为

图3 2Tc掺杂ML-MoS2中的自旋电荷密度分布Fig.3 Spin charge density distribution of 2Tc-doped ML-MoS2

(2)

2.3 与自旋相关的能带结构分析

Tc掺杂ML-MoS2、(Tc,VS)掺杂ML-MoS2和2Tc掺杂ML-MoS2的能带结构如图4所示。由图4可知,无论Tc掺杂还是Tc与VS共掺杂都会使ML-MoS2的带隙变小,这说明Tc原子与VS可以很好地调制ML-MoS2的带隙,同时三个体系都呈现出不同程度的n型半导体特征。由图4可知,在费米能级附近,三个体系自旋向上及自旋向下的能带结构都不具有对称性,说明三个体系都产生了自旋磁矩,这与前面的态密度分析结果一致。

图4 Tc掺杂ML-MoS2、(Tc, VS)掺杂ML-MoS2和2Tc掺杂ML-MoS2的能带结构Fig.4 Band structures of Tc-doped ML-MoS2, (Tc, VS) co-doped ML-MoS2 and 2Tc-doped ML-MoS2

3 结 论

1)Tc掺杂的单层MoS2是一种具有铁磁性的n型半导体。

2)与Tc掺杂ML-MoS2体系相比,VS的引入不会导致(Tc,VS)掺杂ML-MoS2体系的总磁矩发生显著变化, 且掺杂体系磁矩主要由Tc原子贡献。

3)在2Tc掺杂ML-MoS2体系中,通过形成能分析确定出最稳定构型,2Tc掺杂ML-MoS2体系的磁矩为2.048 μB,主要来自于两个Tc 原子。自旋电荷密度分析表明,(Tc-4d)-(S-3p)-(Mo-4d)-(S-3p)-(Tc-4d)耦合链可能是2Tc掺杂ML-MoS2体系发生铁磁耦合的原因。