叶片前后缘识别及百叶轮抛磨工艺研究

2023-12-01杨胜强张晶晶赵旭辉

中国机械工程 2023年22期

琚春刘佳杨胜强张晶晶赵旭辉

1.太原理工大学机械与运载工程学院,太原,030024 2.精密加工山西省重点实验室,太原,030024

0 引言

随着现代发动机性能的提升,涡轮前燃气温度不断提高,对涡轮叶片的冷却设计要求也不断提高,因此,涡轮内部的流动特性和传热特性的研究极为重要,传热特性通常受到边界层转捩、流动分离、表面粗糙度等因素的影响[1]。研究表明,涡轮叶片表面粗糙度增大会影响边界层的传热系数和流动状态,进而影响叶片的传热特性[2-3]。李本威等[4]发现,与光洁较好的涡轮叶片相比,表面粗糙度大的叶片会导致发动机的轴向推力、效率、压比和轴向力矩等特性参数明显降低,造成涡轮整体性能衰退。另有研究表明,叶片前缘的形状对其性能有很大影响,椭圆型前缘和前缘叶身之间的连续性对叶型造成的损失更小[5-7]。目前对镍基高温合金精铸叶片的抛磨通常采用人工抛磨方式,叶片前后缘部位单薄,厚度小,且有着极高的加工精度要求,弦长小于16 mm的叶片要求加工后前后缘轮廓度公差小于0.1 mm,表面粗糙度小于0.8 μm[8]。由于前后缘与叶身曲率变化急剧,现有抛磨方式大多为分区域抛磨,而在区域划分时无法确定前后缘与叶身分界,在抛磨时容易产生过抛、欠抛等现象,故对叶片前后缘区域识别的研究有着重要意义。

叶片前后缘的拟合研究方面,裴景东等[9]在最小二乘法的基础上引入改进粒子群算法进一步求解,提高了拟合精度。张力宁等[10]运用一种基于带约束的最小二乘方法对数据点进行拟合,然后以拟合的结果作为初值,根据椭圆的极线性质进行更精确的求解,该方法具有很好的鲁棒性与精确度。程云勇等[11]通过设定迭代误差对拟合过程进行控制,提出一种考虑叶片纵向光顺要求的各截面椭圆参数调整方法,实现了前后缘椭圆区域光顺曲面的生成。鲍鸿等[12]使用自适应迭代最小二乘法解决了叶片后缘轮廓参数估计误差大的问题。同时,叶片的抛磨需要保证抛磨轮与叶片型面曲率变化高度适应,许多学者对叶片类曲面零件的轨迹规划和柔性抛磨工具开展了大量研究。淮文博等[13]分析了百叶轮抛光机理,提出了影响抛光力的参数为压缩量、转速、初始半径、粒度,并通过设计正交试验得到了百叶轮抛磨力预测模型。毕超等[14]提出了基于柔性砂轮的叶片前后缘柔性磨削工艺方法,进行了柔性磨削探索和实验验证,发现加工后叶片前后缘部位所有截线的加工误差均在允许加工误差范围内。LYU等[15]提出了一种基于材料去除轮廓模型的等残留高度法和一种考虑弹性变形影响的改进等弦高误差法,构造了一种自适应轨迹规划算法,提高了机器人砂带磨削叶片的表面粗糙度、轮廓精度和加工效率。WANG等[16]在经典截面轮廓法的基础上提出了一种新的优化曲线区间算法,在大曲率局部曲面上生成更多的刀位,在小曲率局部曲面上生成更少的刀位,利用优化算法提高了机器人砂带磨削的精度和效率。

国内叶片机器人辅助抛磨技术发展迅速,百叶轮磨削率高,噪声低,具有较强的弹性,自锐性好,耐热耐磨,并且百叶轮抛磨摆脱了柔性砂轮包角小的局限性,适用于叶片前后缘的抛磨。机器人辅助柔性百叶轮抛磨技术利用工业机器人末端夹持叶片,按照规划的轨迹,使叶片与外部高速旋转的百叶轮接触摩擦,达到提高叶片表面质量的目的。本文以某型精铸叶片为加工对象,首先用最小二乘椭圆拟合法识别前后缘,保证抛磨区域的精确性;其次,根据叶片选取良好的弹性抛磨工具百叶轮,分析百叶轮和叶片接触模型中的变形和力,建立抛磨力和百叶轮压缩量的关系;最后利用等弦高误差法和Hertz接触理论确定百叶轮抛磨前后缘的步长和行距,并进行实验验证。

1 叶片前后缘的识别

1.1 最小二乘椭圆拟合法

常用的椭圆拟合方法有两类：一类是基于Hough变换[17]的拟合方法,当拟合点集中在椭圆一侧时,这种方法存在较大误差;另一类是基于最小二乘法的椭圆拟合方法,它是椭圆拟合的基本方法,基本思想是以离散点到所拟合椭圆的距离之和为优化目标,寻找误差最小时的椭圆参数。椭圆的一般方程表达式为

F(x,y)=Ax2+Bxy+Cy2+Dx+Ey+F=0

其中,x、y为椭圆上任意一点的横纵坐标。F(x,y)为关于x、y的函数。A～F为任意椭圆方程未知数的系数。令

W=[ABCDEF]T

X=[x2xyy2xy1]

则优化目标为

|F(xi,yi)|2=min‖WXTW‖2=WTXXTW

式中,(x1,y1),(x2,y2),…,(xi,yi)为所有拟合点的横纵坐标。

由于拟合点不完整或噪声的干扰,上述优化目标的拟合结果可能是双曲线,故要满足椭圆的参数约束：4AC-B2>0。构造拉格朗日函数：

L(W,λ)=WTXXTW-λ(WXTW-1)

式中,λ为方程的特征值。

对以上拉格朗日函数求导得零,转化为求W的特征值和特征向量(λi,μi)的问题,并根据以下条件筛选符合要求的特征向量：

I1=A+CI2=AC-B/4

符合I1I2<0,I1I2>0,I3=0中任一条件的特征向量可以作为椭圆的参数方程。

以某型精铸叶片为对象,使用华朗三维扫描仪扫描叶片得到表面点云,如图1所示,截取Z=145 mm高度处截面轮廓点云,用拟合公差为0.001的样条曲线拟合截面轮廓点得到截面轮廓线,再将曲线以0.05 mm等距离离散化处理,得到后缘及部分叶盆叶背的离散点,如图2所示。

图1 截取叶片截面轮廓Fig.1 Cut section profile of blade

图2 包含后缘及部分叶盆叶背的离散点Fig.2 Discrete points containing trailing edge and part of blade

(a)拟合点过多

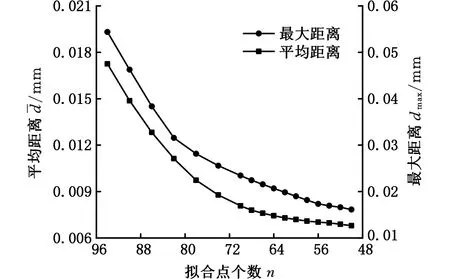
图4 平均距离与最大距离Fig.4 Average distance and maximum distance

图5 斜率差示意图Fig.5 Slope difference diagram

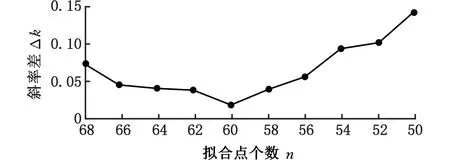
图6 不同拟合点的ΔkFig.6 Δk at different numbers of fitting points

1.2 加噪声数据仿真验证

实际三维扫描仪数据含有一定高斯白噪声,为验证本文算法的准确性和鲁棒性,选取某叶片CAD模型某一截面曲线,并进行等间距加密离散处理,此截面曲线包含的叶片后缘参数如下：中心点坐标(Cx,Cy)=(63.828,48.450)mm,长半轴D1=2.431 mm,短半轴D2=1.354 mm,离心角θ=0.980。添加5种强度不同的高斯噪声N(0,0.0012),N(0,0.0052),N(0,0.012),N(0,0.052),N(0,0.12),并使用上述最小二乘椭圆拟合法对离散点进行椭圆拟合,椭圆参数误差见表1。根据6σ转换原则,三维扫描仪扫描误差0.02 mm相当于标准差为0.0033的高斯噪声,由表1可知误差可以保证在1%以内,由于系统还不可避免地存在其他噪声误差,该方法在添加标准差为0.1 mm的强噪声时拟合误差保证在7%以内,故本识别方法具有良好的抗噪性,并且对叶片前后缘与叶身区域的划分有较高精度。

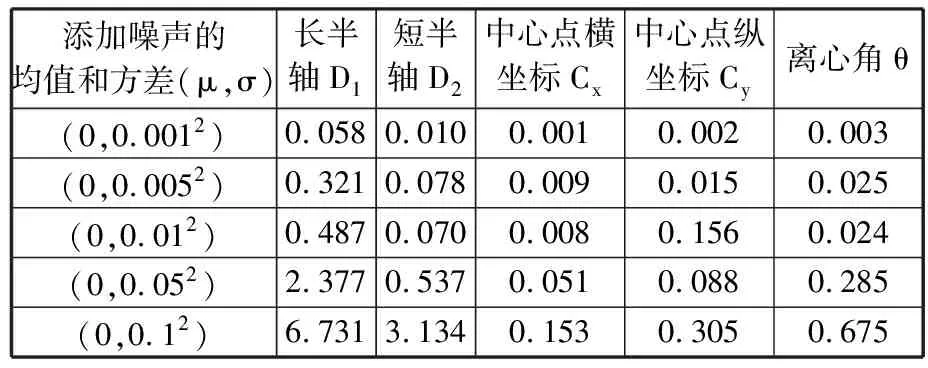
表1 不同噪声强度误差

2 百叶轮压缩量和抛磨力关系建模

2.1 百叶轮压缩过程分析

如图7所示,抛磨时百叶轮与叶片接触瞬间,抛磨系统无接触力产生,当施加一预压力Fn给百叶轮后,百叶轮发生弹性变形δt;增大预压力Fn,磨粒压入叶片,叶片发生弹性变形δwe;继续增大Fn,磨粒压入叶片更深,叶片发生塑性变形δwp,百叶轮高速旋转带动磨粒在叶片表面划擦,叶片表面材料开始去除,抛磨过程开始。

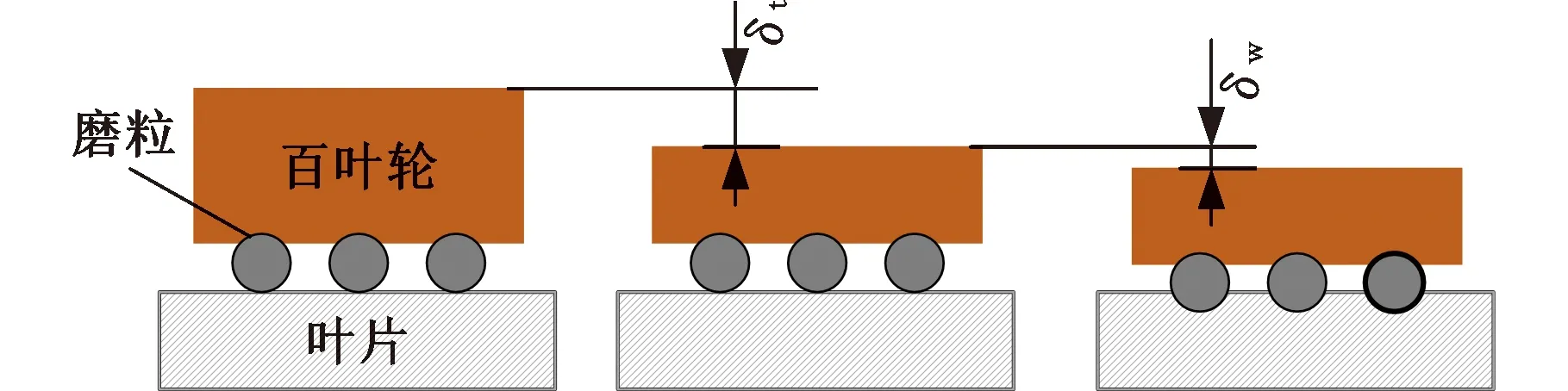
图7 百叶轮抛磨叶片模型Fig.7 Flag wheel and blade polishing model

若要定量分析百叶轮压缩量δt和抛磨力F的关系,需知道百叶轮抛磨系统中所有变形与力的关系。百叶轮抛磨模型受力情况简化为图8,其中,Fn为提前施加给百叶轮的预压力,百叶轮砂布发生弹性变形,将力Fn传递到磨粒,由于磨粒刚性远大于百叶轮砂布与叶片,故此处将磨粒看作刚体,根据磨粒的受力平衡,叶片受到的抛磨力F与预压力Fn相等。F使工件同时发生弹性变形δwe和塑性变形δwp,由以上分析可知：

图8 抛磨受力示意图Fig.8 Polishing force diagram

Fn=F=Fwe+Fwp

δ=δt+δwe+δwp

式中,Fwe为对应弹性变形δwe的力;Fwp为对应产生塑性变形δwp的力;δ为系统的总体变形,包括百叶轮砂布的变形和弹性变形、塑性变形。

2.2 单颗磨粒分析

对百叶轮和叶片接触模型进行以下简化：①百叶轮磨粒为球状;②由于磨粒半径远小于叶片前后缘曲率半径,将叶片抛磨接触区域看作平面;③将磨粒看作刚体,不发生变形。

根据Hertz接触理论[18],如图9所示,将磨粒简化为圆球之后,磨粒压入叶片表面的状态可以看作一个弹性半空间体,接触区域是一个半径为a的圆。其中,δwe为磨粒压入叶片的深度,a为接触圆半径,R为磨粒半径。由Hertz理论,有

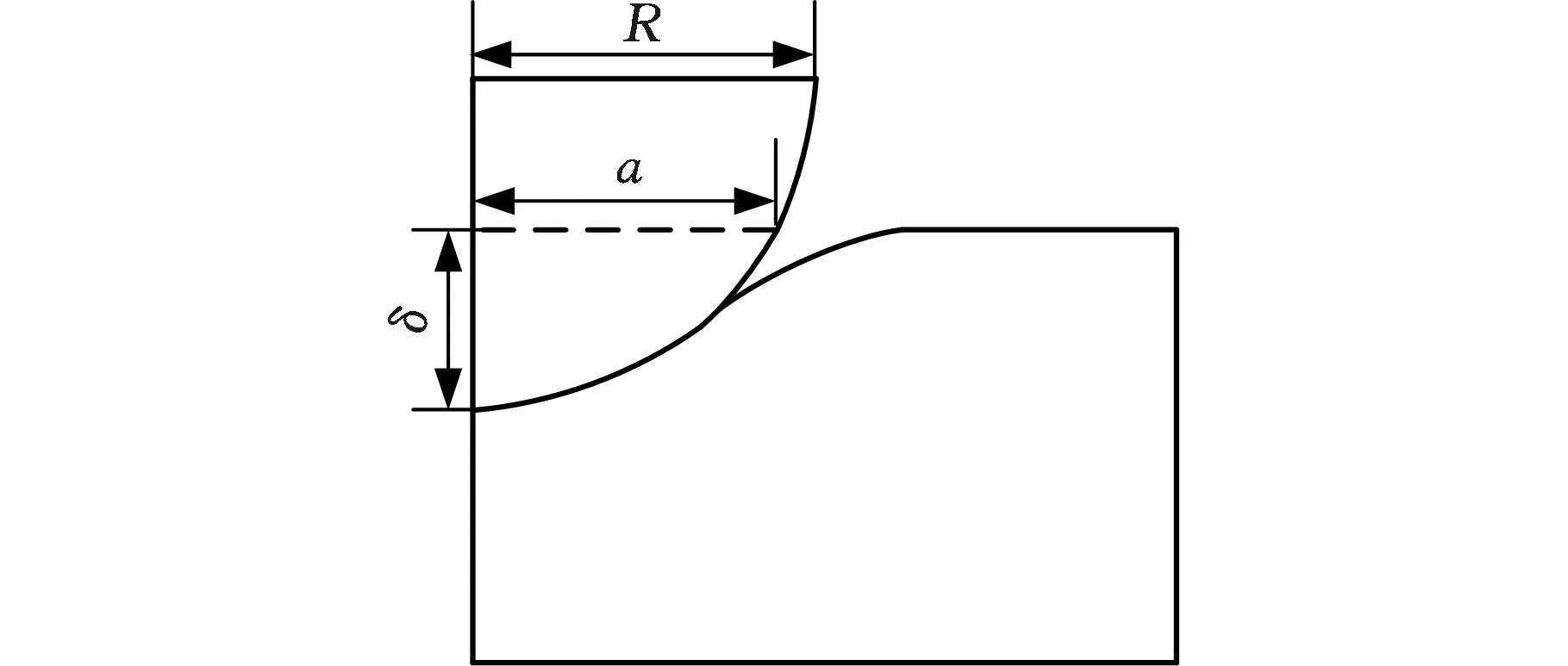
图9 磨粒压入叶片示意图Fig.9 Diagram of abrasive grain pressing into workpiece

a=πF0RE*/(2δwe)=πaF0E*/2

式中,F0为磨粒施加给叶片的最大压力;E*为磨粒和叶片的等效弹性模量;ν1、ν2分别为磨粒和叶片的泊松比;E1、E2分别为磨粒和叶片的弹性模量。

由文献[19]可知,当接触区域中心最大压力达到1.63σy(σy为叶片的屈服强度)时,接触中心正下方0.4811a处开始发生塑性变形,由Hertz接触理论可知,弹性变形与弹塑性变形临界状态发生在压入深度δp=0.4811a时。由文献[20]可知,弹塑性变形与塑性变形的临界压入深度δq=163δp。

磨粒从开始接触叶片到压入深度达到δp之前,叶片发生弹性变形,由Hertz理论可知,压入深度与接触力的关系为

(1)

继续施加压力,叶片同时发生弹性变形和塑性变形。由文献[20]可知,在弹塑性变形状态时,磨粒压入深度和接触力的关系为

(2)

(3)

(4)

式中,Fwep、δwep分别为弹塑性变形阶段的力和压入深度;κ为临界点处的接触应力系数;Fy、ay、δp分别为临界屈服状态时的接触载荷、接触半径和压入深度。

继续施加压力,叶片发生完全塑性变形。由文献[21]可知,发生塑性变形时平均接触压力Pm与接触圆半径、磨粒半径的关系为

Pm=cY=Y(2.845-0.4921a/R)

(5)

其中,Y为材料的屈服应力。又由文献[22],当工件在载荷作用下达到受压的屈服极限σy,此后接触位置的应力不再改变,只能依靠扩大接触面积来承受继续增加载荷,因此有

(6)

根据Hertz理论,球与平面处于完全塑性变形时,接触半径的接触变形的关系为

(7)

联立式(5)～式(7)可得到塑性变形阶段压入深度和接触力的关系。

2.3 多颗磨粒分析

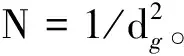
高度方向磨粒分布高度服从正态分布,99%的磨粒在-3σ～3σ之间,其概率密度函数如下：

分别对ψ(z)在弹性、弹塑性、塑性状态下求积分,再与百叶轮表面单位面积内磨粒数相乘可得不同接触状态下参与抛磨的磨粒数。由于每颗磨粒相对于z=0高度不同,无法确定每颗磨粒的压入深度,故以每个阶段的压入深度期望值代表此阶段期望深度。联立以上公式可得到单位面积内总抛磨力F：

F=Fwe+Fwep+Fwp

(8)

在整个系统中,变形δ包括两部分：百叶轮砂布与叶片之间的变形δt及磨粒与叶片接触产生的变形δw。根据以上分析已经得到δw,由Hertz接触理论可得δt：

δ=δt+δw

式中,Ee为百叶轮和叶片的等效弹性模量。

至此已经得到抛磨力F和抛磨过程所有的变形δ之间的关系,但式(8)过于复杂,不利于抛磨时压缩量的设置,需要简化。以320目、磨粒为碳化硅材质的百叶轮和镍基铸造高温合金K403为对象,在MATLAB软件中仿真分析其变形和力的关系,磨粒和K403的材料属性见表2。

表2 磨粒与叶片材料参数

图10所示为单颗磨粒抛磨力与压入深度的关系,可以看出,工件发生的弹性变形量比塑性变形量小两个数量级,因此忽略磨粒与叶片之间的弹性变形量。弹塑性变形和塑性变形曲线近似于直线,且由曲线可知弹塑性变形中曲线下凹的部分为弹性变形量,占比非常小,因此近似将塑性变形量代替叶片的变形。由力的传递及磨粒的受力平衡可知,磨粒与叶片之间的力等于叶片与百叶轮砂布之间的弹性变形力,由图11可以看出,当抛磨力F相同时,工件的变形量远小于百叶轮变形量,因此抛磨系统中的变形量可用百叶轮的变形量表示。

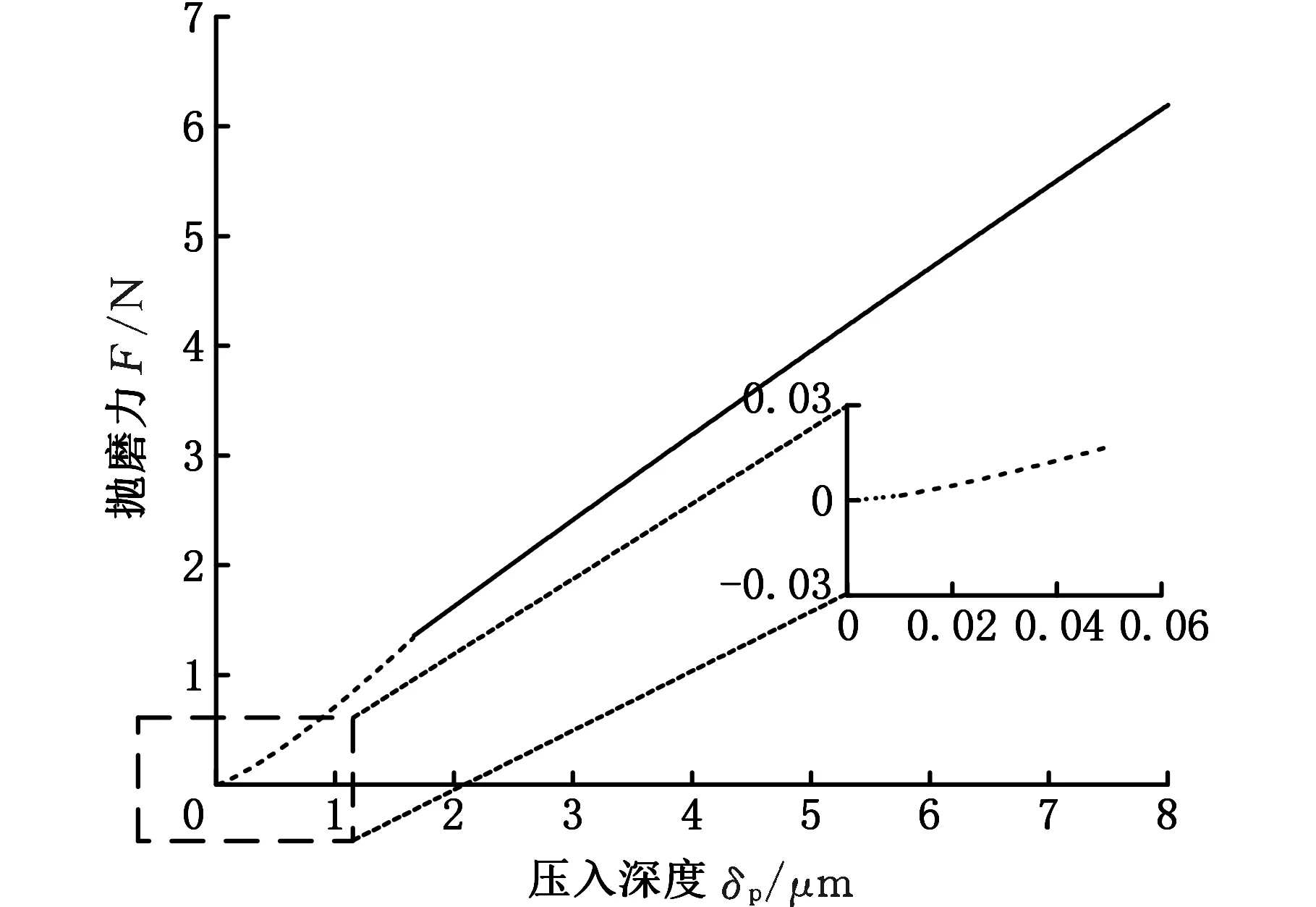
图10 压入深度与抛磨力的关系Fig.10 Relationship between pressed depth and polishing force

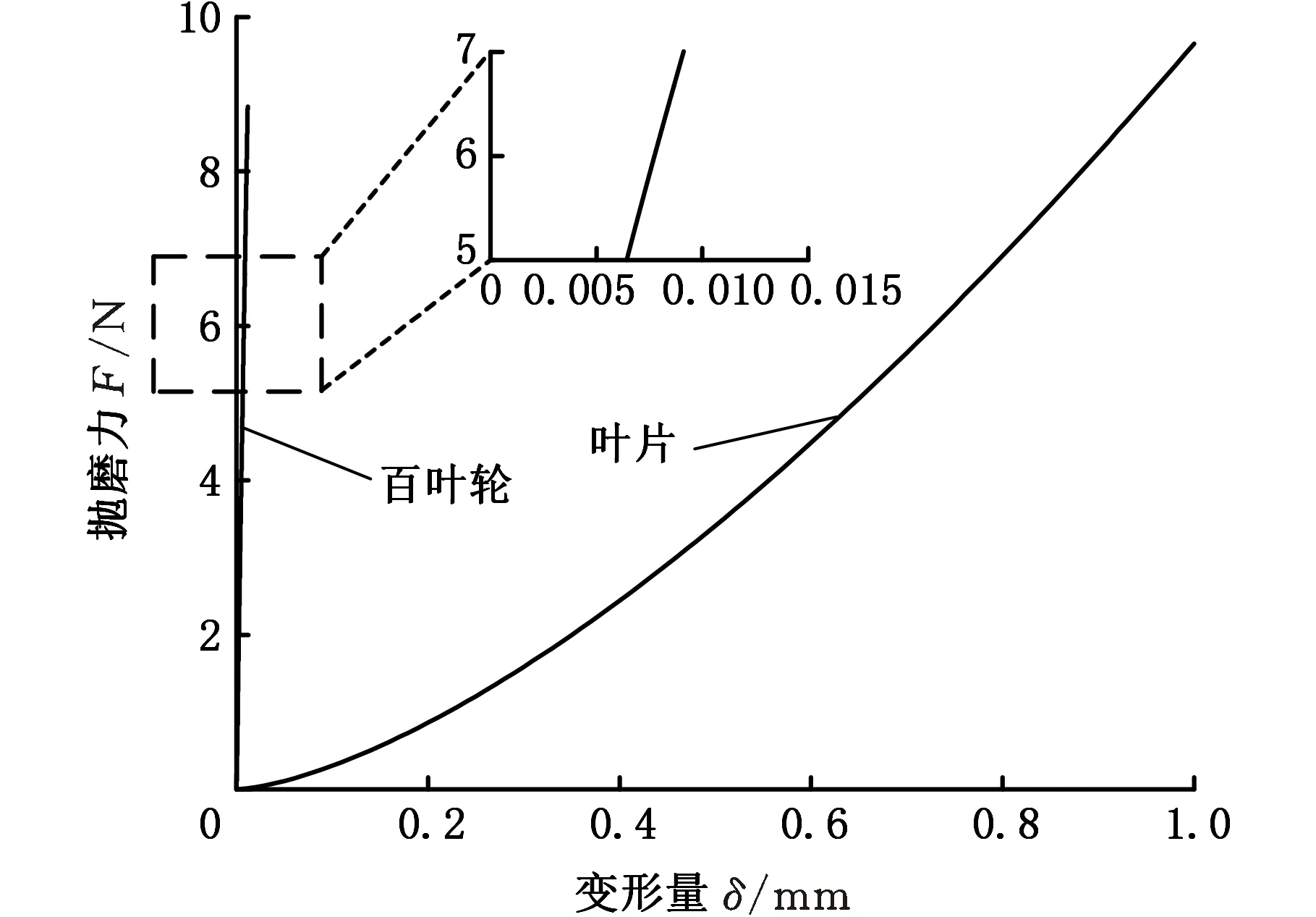
图11 变形与力的关系Fig.11 Relationship between deformation and force

根据Herts理论,用百叶轮砂布与工件之间的弹性变形量δ建立与抛磨力F的关系：

(9)

其中,Eb为百叶轮内部树脂胶和工件的等效弹性模量,由于百叶轮纱布的弹性模量无法得到,可能会对百叶轮的弹性模量有影响,因此设置一比例系数k。

2.4 关系模型实验验证

采用Kwasaki RS20N六自由度工业机器人,末端连接ATI六维力/力矩传感器采集抛磨压力,机器人末端夹持镍基高温合金K403试件,抛磨工具采用直径30 mm、320目,磨粒为碳化硅材质的百叶轮,转速为2900 r/min,预压量分别从0依次增加到1.0 mm,验证百叶轮压缩量与抛磨力关系。

如图12所示,实验曲线为传感器测得百叶轮压缩量从0到1 mm的力,理论曲线为式(9)推导的抛磨力与压缩量的关系,由于k的取值只会影响曲线的陡峭程度,故两条曲线大部分吻合时即为合理的k的取值。当k取0.014时,在百叶轮压缩量为0～0.7 mm时抛磨力与推导关系较为吻合,压缩量为0.7～1.0 mm时实验得到的抛磨力较大,推测其原因是百叶轮压缩量较高,树脂胶轴芯与试件接触力增大,使得力增加,机器人发生振颤,造成力波动较大,因此在抛磨过程中,百页轮压缩量控制在0～0.7 mm时,关系模型较为准确。

图12 百叶轮压缩量与抛磨力的关系Fig.12 Relationship between length of compression and polishing force

3 抛磨路径规划

叶片前后缘由于厚度小,曲率变化大,合理的抛磨轨迹对前后缘的抛磨质量有影响。百叶轮杆与叶展方向平行称为平行抛磨方式,与叶展方向垂直称为垂直抛磨方式;百叶轮进给方向与百叶轮旋转方向相同称为横抛,垂直称为纵抛。如图13所示,针对叶片的曲面特点,以上抛磨方式的行距和步长计算方法主要可分为以下4类：

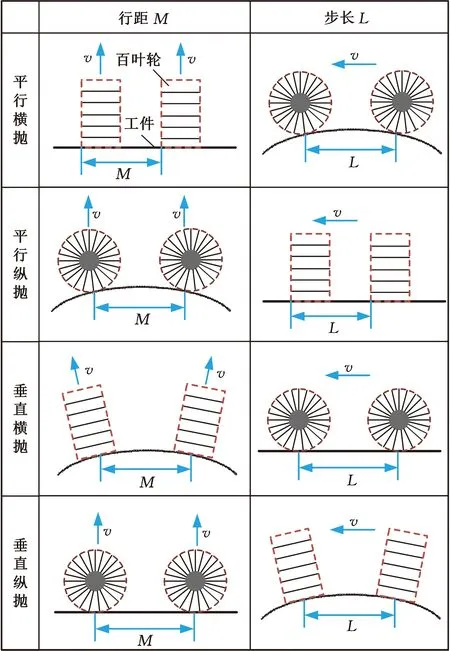
图13 不同方式抛磨示意图Fig.13 Schematic diagram of different ways of polishing

Ⅰ.平行横抛的行距为百叶轮宽度,无需计算;

Ⅱ.平行纵抛、垂直横抛的步长无需计算;

Ⅲ.平行纵抛、垂直横抛和纵抛,根据Hertz接触理论计算行距;

Ⅳ.平行横抛和垂直纵抛,根据等弦高误差法计算步长。

尽管抛磨方式多样,其计算行距和步长的方法主要可分为两类,即基于Hertz弹性接触理论和等弦高误差法的计算方法。

3.1 适用于弹性百叶轮的等弦高误差法

平行横抛和垂直纵抛的步长计算方法可用等弦高误差法,通常情况下等弦高误差法适用于刚性刀具,而叶片抛磨使用的弹性磨具百叶轮的磨削作用小于刚性磨具。因此有必要对等弦高误差法进行改进,图14a为刚性磨具步长计算示意图,由勾股定理可得步长：

(a)等弦高误差法 (b)改进等弦高误差法图14 等弦高误差法Fig.14 Equal chord height error method

图14b为百叶轮抛磨步长计算示意图,Pi、Pi+1为相邻的两个刀位点,h为百叶轮抛磨深度,若采用未改进步长计算方法,h将小于设定弦高ε,出现弦高误差Δδ=ε-h,因此需要将弦高误差δ补偿到设定弦长,此时改进后的弦高ε′=ε+δ,步长为

(10)

根据文献[24],百叶轮的材料去除深度与百叶轮的线速度、压缩量和工件进给速度的关系如下：

h=Kvsap/vf

(11)

其中,K是百叶轮的去除系数,不同尺寸、粒度的百叶轮K值不同。实验使用气动马达驱动百叶轮旋转,气压稳定后转速恒定为2900 r/min,因此选取320目、直径30 mm、磨粒为碳化硅材质的百叶轮设计实验,见表3,测量不同参数下材料去除深度,求得K=0.029 07。

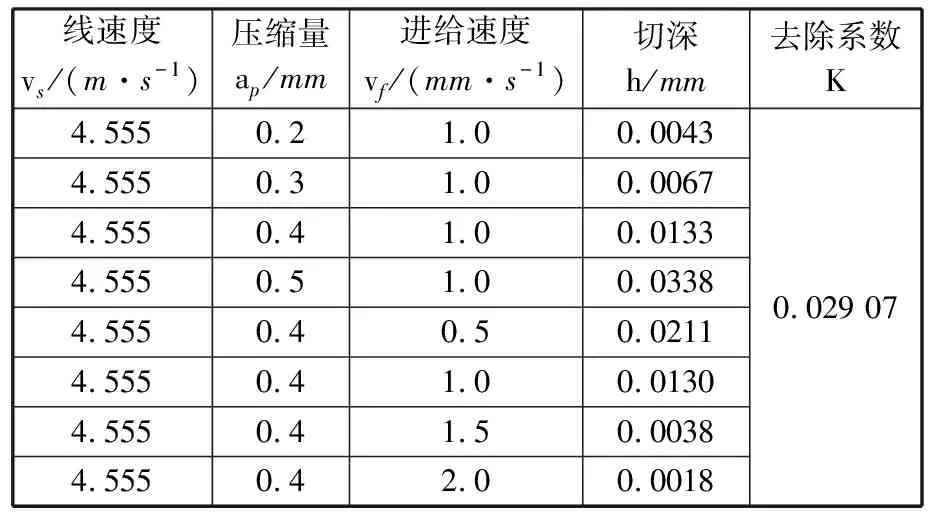
表3 实验安排和结果

将式(11)代入式(10),最终得到步长计算式：

3.2 Hertz弹性接触理论

图15为平行纵抛时百叶轮和叶片的接触简化示意图,抛磨宽度为百叶轮压缩后与叶片接触的接触宽度2a,百叶轮压缩载荷引起的Hertz压力在x方向上的分布为

图15 平行纵抛抛磨示意图Fig.15 Schematic diagram of parallel longitudinal polishing

(12)

由式(12)可知x=0处压力最大,x=-a,x=a时压力减为0。抛磨行距过大会导致叶片表面沟槽明显,抛磨后表面质量不高,减小行距虽然能够提高抛磨精度但降低了抛磨效率。又因恒定的抛磨力可以提升表面质量,因此有必要适当调整行距令抛磨轨迹重叠,使轨迹重叠处两次抛磨压力之和与设定抛磨压力接近,以得到较为恒定的抛磨压力。

分别使两条轨迹重叠半接触长度的0.5、0.6、0.7、0.8、0.9倍,设定抛磨压力为1.9 N,计算叶片x方向重叠区域抛磨压力之和,以抛磨压力之和的最大、最小值相对于1.9 N的浮动范围作为指标,选取合适的抛磨行距。图16所示为重叠0.8倍半接触长度时的压力之和,其中最大压力2.29 N,最小压力1.53 N,误差范围±0.4 N。由图17可知,随着重叠倍数的增加,最大抛磨力趋于设定抛磨力1.9 N,最小抛磨力远离1.9 N,重叠倍数为0.8时误差波动范围达到最小值,此时前后缘的材料去除最均匀,因此行距为0.8倍半接触长度时最适合抛磨。

图16 0.8倍半接触长度时的抛磨力Fig.16 Polishing force at 0.8 times half contact length

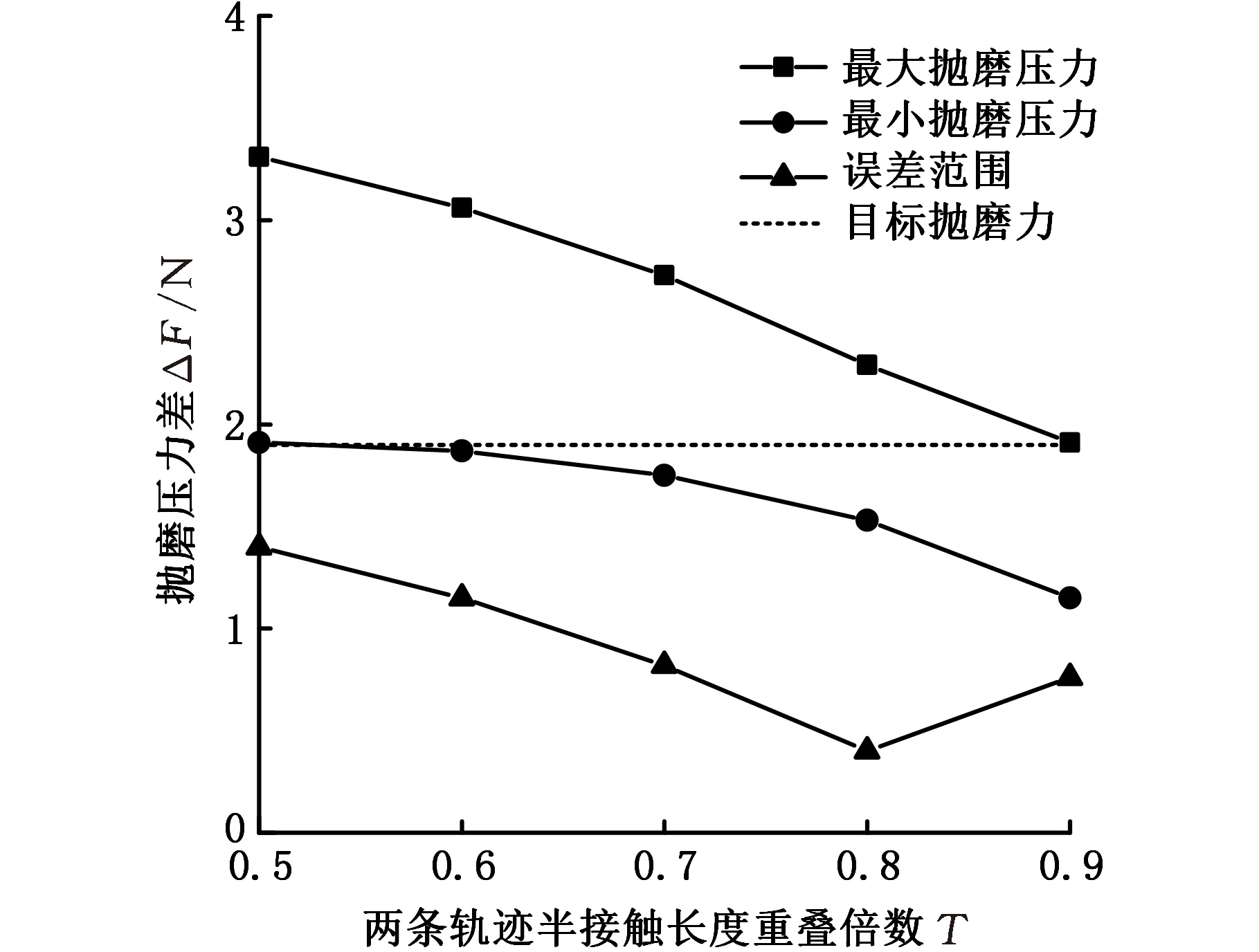
图17 压力误差Fig.17 Error of pressure

4 实验

前后缘的精确识别与抛磨轨迹的选择对叶片抛磨质量有着重要影响。针对上文提出的4种抛磨方式,根据不干涉原则与最大型面贴合原则,设计了机器人辅助百叶轮抛磨叶片前后缘实验,以分析不同抛磨方式对叶片表面质量的影响。若采用垂直抛磨方式,抛磨靠近叶根部位的前后缘时,叶片榫头与百叶轮发生干涉,不能做到一次完整抛磨,因此设计平行横抛方式抛磨叶片后缘,行距计算方法采用等截面法,即用一组平行的截面截取叶片后缘生成加工路径,如图18所示,在每条路径上根据改进的等弦高误差法计算步长;采用平行纵抛方式抛磨叶片前缘,行距为0.8倍半接触长度。使用超景深显微镜检测抛磨前后叶片前后缘表面形貌,由图19可以看出,抛磨前叶片前后缘表面存在较明显的划痕、凹坑和凸点,抛磨后表面出现密集的抛磨纹路,且无灼伤痕迹。

(b)后缘图19 前后缘抛磨前后表面对比Fig.19 Surface comparison before and after leading and trailing edge polishing

沿叶展方向抽取5个截面,使用Perthometer m2便携式粗糙度仪分别在抛磨前后进行测量。图20所示为截面粗糙度测量结果。可以看出,采用横抛和纵抛工艺对叶片前后缘抛磨之后,粗糙度均有明显降低。其中前缘粗糙度平均值从1.153 μm降至0.239 μm,后缘粗糙度平均值从1.236 μm降至0.301 μm。由此可见,横向抛磨和纵向抛磨对叶片前后缘表面粗糙度的降低都有明显效果。

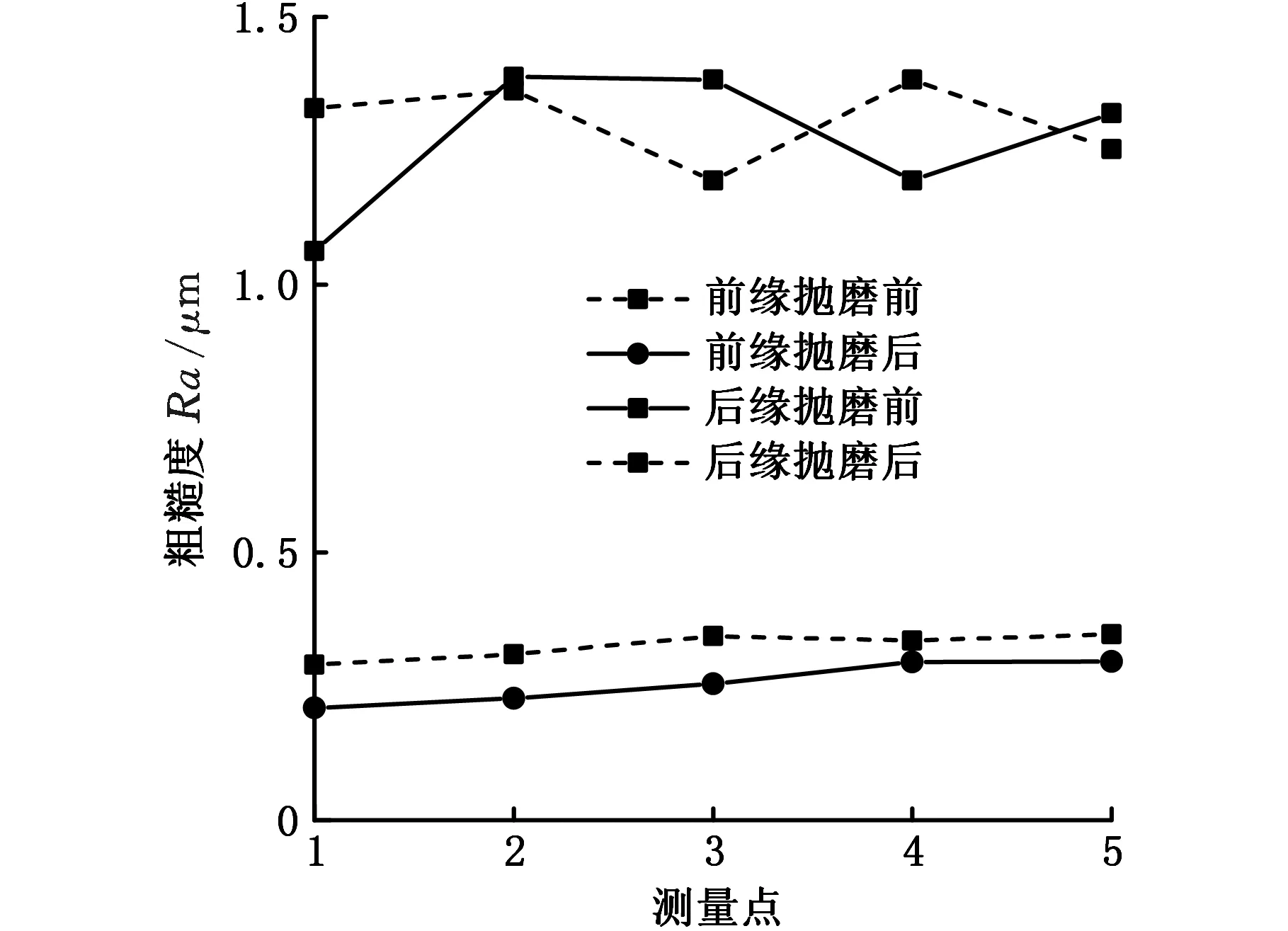
图20 前后缘抛磨前后粗糙度Fig.20 Roughness before and after leading and trailing edge polishing

沿叶展方向抽取5个截面,使用超景深显微镜分别检测抛磨前后截面线轮廓度误差。由图21可知,前缘轮廓度误差平均值从0.140 mm降至0.073 mm,后缘轮廓度误差平均值从0.133 mm降至0.070 mm,表明百叶轮对叶片抛磨叶片前后缘对降低其轮廓度误差有显著作用。其中,前缘轮廓度误差最大、最小值之差从0.028 mm降至0.014 mm,后缘从0.022 mm降至0.010 mm,表明百叶轮抛磨提高了前后缘的轮廓精度,由图22可以看出抛磨后的前后缘轮廓截面更为光滑。