考虑载荷交互影响的非均匀损伤累积模型

吴志峯 高建雄 徐蓉霞 朱鹏年

新疆大学机械工程学院,乌鲁木齐,830017

0 引言

构件可能受到不同负载的作用而导致损伤累积,其中因交变载荷持续加载而产生的疲劳破坏占据大多数[1],占失效概率的80%～90%,因此,如何精准预测构件的疲劳寿命是当下亟待解决的重大问题。机械构件在服役历程中承受的载荷异常复杂,而交变载荷疲劳寿命试验数据相对较少,相反地,恒幅载荷疲劳寿命试验目前已积累了大量的试验数据。利用损伤等效法则结合恒幅载荷试验数据可预测交变载荷疲劳寿命[2]。

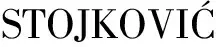
本文首先提出一种恒幅载荷下基于剩余寿命的非均匀疲劳损伤理论,然后阐述了载荷加载次序效应,并证明该非均匀损伤模型可考虑载荷加载次序效应。再次验证了载荷间的相互作用,提出相邻两级载荷存在相互影响,定义并引入了载荷交互影响因子,提出了等效损伤新模型。最后将非均匀损伤模型与等效损伤新模型结合,构造了多级变幅载荷下的非均匀损伤模型。

1 非均匀损伤累积模型

Miner法则认为损伤是均匀的,例如在恒幅载荷加载下,该法则认为每次循环产生的损伤是1/Nf,Nf是构件的疲劳寿命。实际上,材料的性能劣化促进损伤累积的进程,在损伤演化初期,每次循环产生的损伤相对较少,后期损伤相对较大。基于材料的剩余疲劳寿命,可认为载荷第一次循环造成的损伤为1/Nf,第二次循环造成的损伤为1/(Nf-1),以此类推,载荷第n次循环造成的损伤为1/(Nf-n+1),Nf可由S-N曲线求得。此时,面临的问题为循环次数n=N时,单次循环造成的损伤Di=1,即构件失效的所有损伤均由最后一次循环造成,这与事实不符。一般认为损伤是一个从0到1持续增加的数值。本文定义损伤D=Dr/Dc。Dr、Dc可表示为

(1)

(2)

综上所述,本文定义的损伤D可表示为

(3)

式(3)即恒幅载荷下的非均匀损伤模型的原理式。根据积分思想,式(3)可近似为

(4)

式(4)为恒幅载荷下的非均匀损伤模型的简易计算形式。

多级载荷下的寿命预测需要恒幅载荷下的损伤累积模型与损伤等效法则相结合,损伤等效法则如图1所示。

图1 等效损伤法则示意图Fig.1 Schematic diagram of equivalent damage law

(5)

联立式(4)与式(5),可估算两级载荷下的疲劳剩余寿命：

n2=(Nf1-n1)lnNf2/lnNf1

(6)

在两级载荷的剩余寿命基础上进行迭代,可得到三级载荷下的疲劳剩余寿命：

n3=[(Nf1-n1)lnNf2/lnNf1-n2]lnNf2/lnNf1

(7)

根据式(7),在三级载荷加载下的剩余寿命基础上进行迭代计算,可得到任意多级载荷下的疲劳剩余寿命表达式：

ni={[(Nf1-n1)lnNf2/lnNf1-n2]lnNf3/lnNf2-

…-ni-1}lnNfi/lnNf(i-1)

(8)

式(8)为多级载荷下的剩余寿命预测模型,此模型的未知参数相对较少,形式上非常简洁,具有一定的工程应用价值。

2 载荷间的交互影响

2.1 载荷加载次序效应的阐述

疲劳失效是一个极度复杂的物理过程,Miner法则从疲劳失效机理上进行了简化。金属材料的失效机理中包含了多种影响因素,且损伤变量与载荷变量之间表现出高度的非线性相关,损伤累积变量可描述为

D=F(σ,n,f,T,ϑ,κ,τ,ζ)

(9)

式中,σ为平均应力;f为载荷加载频率;T为环境温度;ϑ为环境湿度;κ为与金属材料属性相关的系数;τ为与结构特征相关的函数;ζ为与其他环境因素相关的系数。

在实际工况下,载荷加载频率、金属材料性能、结构细节特征等因素已给定,空气湿度与环境温度相对稳定,则式(9)可简化为

D=F(σ,n)

(10)

以两级循环载荷为例,非线性损伤演化曲线如图2所示。

图2 D-n非线性损伤演化曲线Fig.2 D-n nonlinear damage evolution curve

对式(10)进行偏微分,可得到损伤演化方程：

(11)

若载荷加载次数用累积损伤表示,则式(11)可表示为

(12)

为便于表达,特规定符号φ(D),可令

(13)

由式(13)可得

=φ(D)φ(σi)

(14)

式(14)等号两边对D偏微分并进行数学形式变换,可得

(15)

由式(15)可知,f(D,σi)是一个关于D和σi的可分离函数。f(D,σi)的分离性决定了损伤模型不具备载荷加载次序效应。特别地,就Miner法则而言,其损伤演化方程式可表示为

f(D,σi)=1/Nfi

(16)

结果可发现,Miner法则的损伤演化函数为一个载荷变量,具备可分离性。文献[2]指出,载荷变量与损伤变量的不可分离性是产生载荷加载次序效应的前提条件,因此Miner法则不具备载荷加载次序效应。根据式(15)和式(16),线性损伤累积法则和非线性损伤累积法则不具备载荷加载次序效应的根本原因是损伤演化函数的可分离性。

基于剩余寿命的非均匀损伤累积模型的损伤演化函数可表示为

(17)

将Basiquin公式代入式(17)可得

(18)

由式(18)可知,基于剩余寿命的非均匀损伤模型的损伤演化函数具备载荷变量与损伤变量的不可分离性,因此,该模型具备载荷加载次序效应。

2.2 考虑载荷间交互影响的等效损伤模型

疲劳损伤的破坏机理极为复杂,断裂力学理论认为,疲劳进程由内因和外因共同推进,应力强度因子k(σ,a)是描述整个疲劳失效过程的控制参量,其中σ为外加载荷,是推进疲劳进程的外因;a为裂纹长度,相当于损伤变量,是推进疲劳进程的内因。这种失效准则被称为“二元失效判据”。由式(10),以载荷循环比表征损伤变量,可得到损伤变量的函数表达式：

(19)

传统的损伤等效模型表达式可定义为

(20)

文献[14]指出,对于高层错能材料,高、低载荷加载产生的疲劳机理有所不同;对于低层错能材料,高、低载荷加载产生的位错结构也有所不同。因此,传统意义上的损伤等效模型的等效机理并不充分,不同应力水平下的等效损伤点并不存在。根据上述观点,可认为式(20)的等效机理存在一定局限性。

一般认为,当载荷为高-低顺序加载时,高载荷会破坏材料的晶粒结构,使裂纹提前形成,对损伤累积有促进作用。低-高顺序加载下,低载强化效应会阻碍损伤的发展。因此,可认为相邻两级载荷间存在交互影响。有研究指出[15],不同应力水平下的损伤演化规律会相互影响,前级载荷会影响后级载荷的损伤累积进程。

高-低载荷加载时,高载荷的持续加载使裂纹提前形成,如图3所示,高载荷的持续作用干涉低载荷的损伤演化趋势,假设未干涉前的损伤演化趋势为AF,则干涉后的损伤演化趋势应为AH,即此干涉作用可促进损伤趋势的发展。

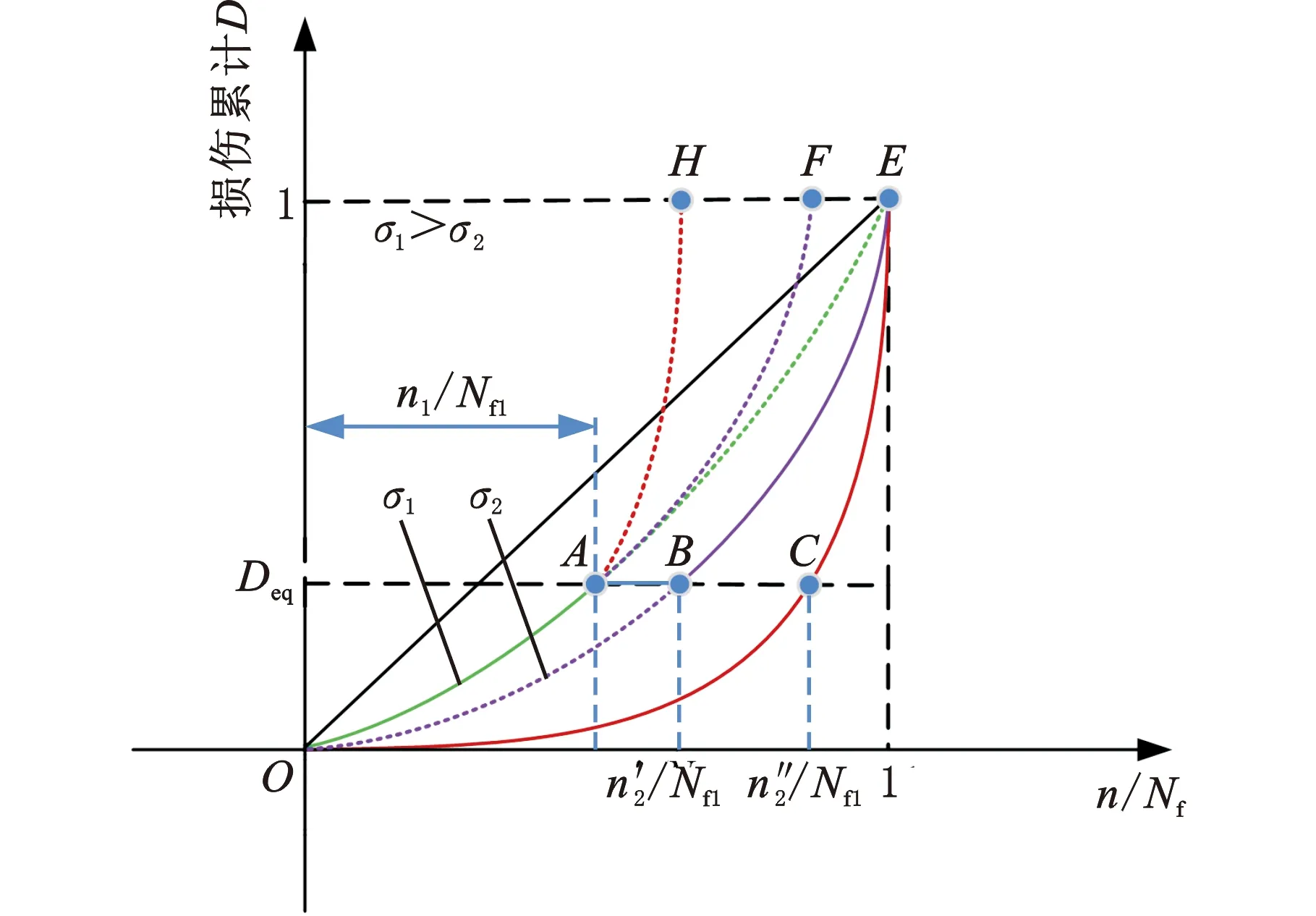
图3 高-低加载D-n/N损伤演化曲线Fig.3 High-low loading D-n/N damage evolution curve

将曲线AH平移到E点并进行延伸,可得到一条损伤曲线OCE,与曲线OBE不同的是,OCE这条曲线考虑了前级载荷对后级载荷的影响,假设此曲线的损伤方程与式(19)相似,可令其为

D=Φ(n/Nf,σ2)

(21)

根据损伤等效法则,构件在应力σ1下加载n1次产生的损伤等效于应力σ2下按照曲线OCE单独作用n2″ 次产生的损伤。如图3所示,考虑载荷间交互作用的损伤演化路径为OA→AC→CE,相应的损伤等效方程式可表示为

(22)

损伤曲线OCE是以曲线OBE为基础构造的,且F(n/Nf,σ)和Φ(n/Nf,σ)均与n/Nf有某种幂函数关系,因此可以假定Φ(n/Nf,σ)可由F(n/Nf,σ)改变幂指数来得到,故其方程可表示为

Φ(n/Nf,σ)=[F(n/Nf,σ)]ω

(23)

式中,ω为载荷交互因子,用于表征上级载荷与后级载荷之间的交互影响效应。

由图3可知,高-低加载时,ω>1;反之,低-高加载时,ω<1;若是恒幅加载,则不存在载荷间的交互影响效应,即ω=1。文献[16]认为,相邻两级载荷间,载荷水平相差愈大,载荷间的交互影响愈显著。根据以上分析,可将交互影响因子定义为

其中,σi为第i级载荷对应的疲劳寿命。则式(23)可表示为

(24)

为方便书写,特规定如下符号：

(25)

根据式(25),结合式(24),推广至任意多级载荷下的等效损伤新模型,模型表达式为

(26)

式(26)为考虑载荷交互影响的等效损伤模型,相较于传统损伤等效模型,新模型弥补了传统模型忽略载荷交互影响的缺陷。

2.3 多级载荷下的损伤累积模型

式(8)形式简便,且未知参数较少,但它是基于恒幅载荷下的非均匀损伤模型与传统损伤等效模型相结合建立的,其局限性在于忽略了载荷间的交互影响。基于剩余寿命的非均匀损伤模型与等效损伤新模型相结合,构造考虑载荷交互影响的非均匀损伤累积模型可弥补这一局限。

以两级载荷为例,将式(8)与式(26)结合,构建考虑载荷间交互影响的非均匀损伤累积模型的表达式：

(27)

其中,下标mp代表改进模型。以两级载荷下的表达式为基础进行迭代,可得到三级载荷下的损伤累积模型表达式：

(28)

根据式(28),将其推广至任意多级载荷下的考虑载荷交互影响的非均匀损伤累积模型,模型表达式为

(29)

式(29)为多级载荷下的考虑载荷交互影响的非均匀损伤累积模型的一般函数式,此形式结构简单,未知参数较少,且可通过S-N曲线进行求解,在工程应用中较为实用。

疲劳寿命预测模型为

(30)

3 算例验证与分析

以文献[17]中Al-2024-T45合金和文献[18]中30NiCrMoV12钢试验数据来验证本文模型的正确性。30NiCrMoV12钢的抗拉强度为1035 MPa,疲劳极限为391 MPa,试件经过回火及硬化处理,疲劳寿命数据见表1。

表1 30NiCrMoV12钢疲劳试验寿命

Al-2024-T45合金具有高强度、耐高温的特点,被广泛应用于航空航天领域,用来制作例如飞机螺旋桨、蒙皮、翼肋等零部件,其疲劳寿命试验数据见表2。

表2 Al-2024-T45合金疲劳试验寿命

载荷加载方式为应力控制,应力比R=-1,试验加载参数见表3、表4。由表3、表4可发现,模型式(30)的预测精度最高,预测稳定性最强,模型式(8)的精度和稳定性相对较差,但仍满足使用要求。Corton-Dolan模型的预测精度与稳定性接近Miner法则,且能满足使用要求,但预测精度稍显不足。

表3 Al-2024-T45合金疲劳试验数据及模型对比

由图4、图5可以发现,式(8)模型和式(30)模型的预测值都分布在1.5倍的公差带内,证明了所提模型的可行性,其中式(30)模型的预测稳定性相对较高。

图4 Al-2024-T45合金疲劳寿命及各模型对比Fig.4 Fatigue life of Al-2024-T45 alloy and model comparison

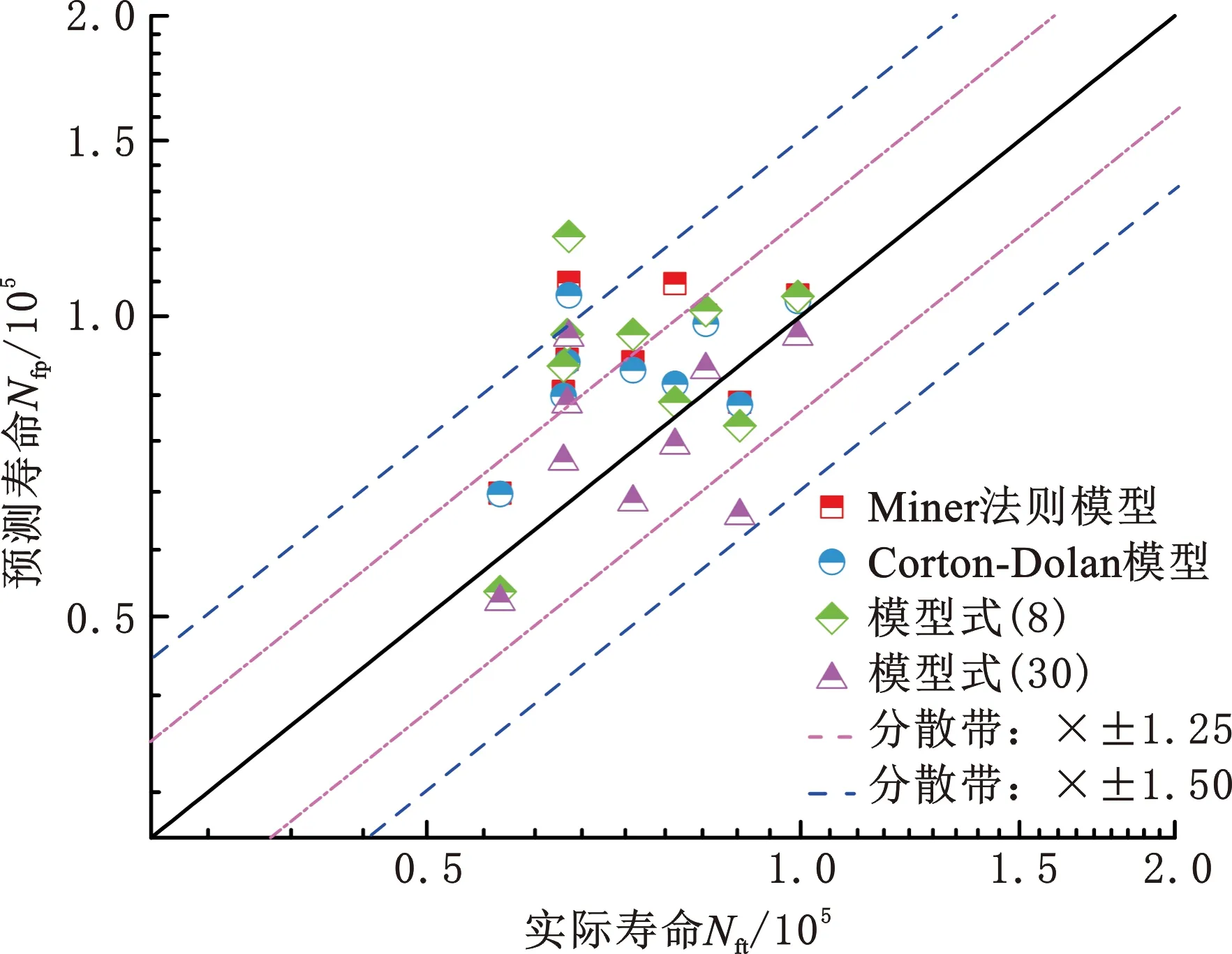
(a)前8行数据

式(8)与式(30)之间的差距在于是否考虑载荷间的交互影响,通过试验分析证明载荷间的交互影响是影响预测精度的重要因素,且这种影响会随着载荷加载次数的增多变得越来越大。实际情况下,构件承受的载荷异常复杂,载荷间的交互影响非常大,这也是Miner法则在使用中不满足精度要求的重要原因。

4 结语

本文针对变幅载荷加载过程的复杂性,从剩余寿命出发建立恒幅载荷下的非均匀损伤累积模型,结合传统损伤等效模型与考虑载荷间交互影响的损伤等效新模型分别建立多级载荷下疲劳寿命预测模型和多级载荷下考虑载荷交互影响的疲劳寿命预测模型,将模型应用于两级载荷加载中,通过与试验数据的对比,验证了模型具有较高的寿命预测精度。