素养导向下对一道2023 年高考试题的溯源探究与推广

福建省武夷山第一中学(354300)葛香珠

福建省南平市高级中学(353000)江智如 蔡珺

1 试题呈现

焦点三角形是圆锥曲线的重要性质,包含丰富的圆锥曲线背景知识,常作为情景载体出现在历年的高考试题中,文[1]给出了此类题型的解题策略.2023 年全国高考新课标Ⅰ卷第16 题是以焦点三角形为载体,求解离心率的题型,解题思路多样,方法巧妙,全方位反映双曲线的几何特征.

题目(2023 年高考新课标Ⅰ卷第16 题) 已知双曲线C:的左、右焦点分别为F1,F2,点A在C上,点B在y轴上,则C的离心率为____.

2 试题溯源

笔者查阅相关资料,发现本试题与2020 年全国高中数学联赛福建省预赛第5 题如出一辙,几乎就是同一题型,试题如下:

溯源题目1(2020 年全国高中数学联赛福建省预赛5)设F1,F2为双曲线C:(a＞0,b＞0)的左、右焦点,过F2的直线l交双曲线C的右支于A、B两点,且则双曲线C的离心率为____.

评析题目1 与高考试题的已知条件比较相似,区别在于:高考试题把题目1 中的点B换在y轴上,把题目1 中的焦点直角三角形更换为F1A与F1B的垂直关系.两道试题考查的难点都是如何利用“垂直”与“向量”关系求解离心率.二者考查的目标与解题思路一致,都是考查双曲线定义与几何性质相关知识,考查考生数学阅读能力、数形结合思想、推理论证能力和运算求解能力[4].

3 试题解析

思路1(从解三角形角度入手)如图1,设|AF2|=2m,则|BF2|=3m.因为点O为F1F2的中点,且点B在y轴上,所以|BF1|=|BF2|=3m.又|AF1|-|AF2|=2a,故|AF1|=2a+2m.

图1

在RtΔABF1中,F1A⊥F1B,故9m2+(2a+2m)2=25m2,化简得(a+3m)(a-m)=0,故a=m或a=-3m(舍去),所以|AF1|=4a,|AF2|=2a.又|BF2|=|BF1|=3a,故|AB|=5a,从而cos ∠F1AF2=因此,在ΔAF1F2中,由余弦定理得,cos ∠F1AF2=整理得5c2=9a2,因此,C的离心率为

思路2(从坐标运算角度入手)由已知可设F1(-c,0),F2(c,0),A(x0,y0),B(0,t),则由即化简得又0,化简得t2=4c2.

又点A在双曲线C上,则=1,去分母得,25c2b2-16c2a2=9a2b2,即25c2c2-a2-16a2c2=9a2(c2-a2),化简得25c4-50c2+9a4=0,于是(5c2-9a2)(5c2-a2)=0,解得5c2=9a2或5c2=a2,从而故又e＞1,所以

思路3(从三角形相似角度入手)如图2,过点A作AC⊥x轴于点C,则ΔBF2O∽ΔAF2C,于是令AC=h,则又OF2=c,故从而因为∠BF1A=90°,得ΔAF1C∽ΔF1BO,所以化简得从而在RtΔAF2C中,AF2=在RtΔAF1C中,AF1=故由双曲线定义得,AF1-

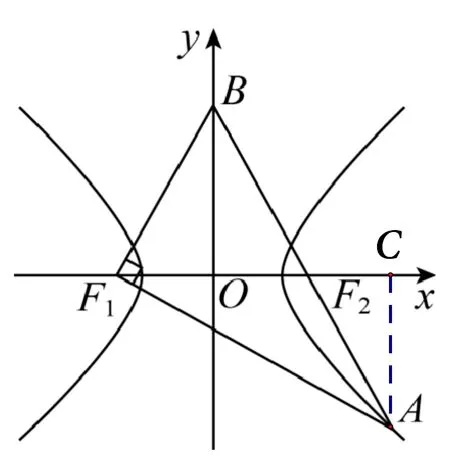
图2

评析本试题考查双曲线的定义与几何性质相关知识,背景知识是圆锥曲线的焦点三角形相关性质,考查范围来源于教材,又高于教材.试题将平面向量与解析几何等知识综合应用做了较好的设计,通过问题的简单情境,依据双曲线的定义分析问题,探索解题思路.解答过程繁简适度,体现思维的灵活性.试题提供多种思考角度,为不同能力的考生构建展示平台.思路1 从解三角形角度入手,面向大部分考生,考生只须把“垂直”与“向量共线”关系转化为a,c关系便可解决问题.思路2 从坐标运算角度入手,体现解析几何的通性通法.思路3 从三角形相似关系入手,计算量小,方法巧妙,要求考生有扎实的数学功底.不同层次的考生可以根据自身的能力水平找到不同的解题思路与方法,对数学运算和逻辑推理等数学核心素养的考查有较好导向作用,体现试题的区分与选拔功能.

4 试题推广

根据思路1,我们把试题已知条件中的向量系数一般化,将试题结论进行推广,可以得到结论1:

结论1已知双曲线C:的左、右焦点分别为F1,F2,点A在C上,点B在y轴上,则C的离心率

证明设|F2B|=t,则|F2A|=λt,从而|F1A|=λt+2a,|F1B|=t.因为F1A⊥F1B,所以在RtΔABF1中,|F1A|2+|F1B|2=|AB|2,即t2+(λt+2a)2=(λt+t)2,展开得2a2+2aλt=λt2.又在ΔAF1F2中,

而

故联立得

即

因为

所以

于是

故

因此,结论1 是试题的推广.此外,类比椭圆的定义与几何性质,我们还可以将结论1 推广到椭圆的情形,得到结论2,限于篇幅的限制,证明过程就留给读者来完成.

结论2已知椭圆Γ:的左、右焦点分别为F1,F2,点A在Γ 上,点B在y轴上,则Γ 的离心率e=

5 高考链接

题目1 解析如图3,设|AF2|=t,则依题意有|BF2|=2t,从而|AB|=3t|AF1|=t+2a,|BF1|=2a+2t.因为知AF1⊥AF2,所以

图3

即

题目2(2016 年高考ⅠⅠ卷理科第11 题)已知F1,F2是双曲线E:的左、右焦点,点M在E上,MF1与x轴垂直,则E的离心率为()

解析如图4,在Rt △MF1F2中,∠MF1F2=90°,因为所以cos ∠MF2F1=于是又点M的横坐标为-c,且点M在双曲线上,故可求点M的纵坐标为为从而

图4

而e＞1,解得因此,选择A.

评析本试题重点考查考生对双曲线基本概念、性质以及双曲线和直线位置关系的理解与掌握情况,并结合双曲线定义与焦点三角形的度量关系,考查考生直观想象的数学核心素养.需要考生有清晰的逻辑思维能力、良好的直观想象能力、知识的综合理解能力.此外,本试题也具有较好的选拔功能与良好的区分效果,凸显数学课程标准的基本理念与要求[3],对教学实践有导向作用.

结束语在高考评价体系指引下,高中圆锥曲线的教学应由传统的“结果性教学”转变为素养立意的“过程性教学”,这就要求学生不仅要知其然,更要知其所以然,同时引导学生探究问题的“本源”,学会举一反三,夯实数学基础.一方面,教师探寻几何问题的本“源”,追溯数学思维发展的源泉,可以提升教师自身数学专业素养和专业化水平[4];另一方面,教师把握几何问题的“流”,登高望远,拓展视野,培养学生思维的深度和广度,设置精致练习[5],摒弃“题海战术”,提高数学学习的兴趣,挖掘数学学习的潜能,提升学生数学综合素养[6].