一道斜率之积为定值的解析几何试题探究与推广

广东省华南师范大学附属中学汕尾学校(516600)刘光明

爱因斯坦提倡“探索真理比占有真理更为可贵”,解析几何问题无论是解答方法的相似性还是结论的可类比性都深深的吸引着广大数学爱好者.本文通过对一道斜率之积为定值的解析几何试题进行多解阐述,运用类比思想在双曲线和抛物线情境中进行相应的结论探索,借助几何画板动态探索其相关的逆命题情况,经过严谨的数学逻辑推理得到了一些相关结论,梳理成文,与数学爱好者交流.

1.试题呈现与解答

题目已知椭圆C:的离心率为且过点过C的右焦点F且不与x轴重合的直线C交于P,Q两点.

(1)求C的方程;

(2)设C的左顶点为A,直线AP,AQ和直线l:x=a分别交于点M,N,记直线MF,NF的斜率分别为k1,k2,求证:k1·k2为定值.

解第(2)小问解答:设P(x1,y1),Q(x2,y2),由题意可设直线PQ的方程为x=ty+1,将其与椭圆方程联立并消去x可得(t2+2)y2+2ty-1=0,则

故

又直线AP的方程为从而得到点M坐标为同理可得点

于是直线MF和直线NF的斜率分别为

因此

将(*)代入可得

因此k1·k2为定值-4.

评注“设而不求”是解决直线与曲线相交这一解析几何问题的通法,思维层次要求不高,但运算推理能力要求较高.

2.结论推广

2.1 椭圆中的推广

结论1椭圆Γ:= 1(a＞b＞0)的左顶点为A.过其右焦点F的直线l(与x轴不重合)与椭圆Γ 相交于P,Q两点,直线AP,AQ和直线x=a分别交于点M,N,记直线MF,NF的斜率分别为k1,k2,则k1k2=-4.

结论1 的证明可以参照前面试题的解法进行推导证明,在此不作赘述.通过几何画板动态演示可得其更一般的结论也是成立的,详细阐述见结论2.

结论2如图1,椭圆Γ:= 1 (a＞b＞0) 的左顶点为A,点E(m,0),P,Q是Γ 上的两点,直线AP,AQ和直线x=t分别交于点M,N,记直线EM,EN的斜率分别为k1,k2.与x轴不重合的直线PQ过点E的充要条件是

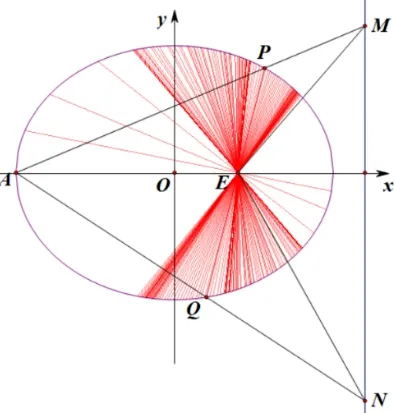
图1

证明首先证明必要性.设P(x1,y1),Q(x2,y2),直线PQ的方程为x=ny+m,将其与椭圆方程联立消去x可得

由题意Δ＞0,则

又直线AP的方程为令x=t可得点M的纵坐标为同理可得因此

以下证明充分性.设P(x1,y1),Q(x2,y2),直线PQ的方程为x=ny+k,将其与椭圆方程联立消去x可得

由题意Δ＞0.故

又直线AP的方程为令x=t可得点M的纵坐标为即点M坐标为同理可得点于是

结论2 中,令m=c,t=a,

2.2 双曲线中的推广

结论3如图2,双曲线Γ:的左顶点为A,点E(m,0),P,Q是Γ 上的两点,直线AP,AQ和直线x=t分别交于点M,N,记直线EM,EN的斜率分别为k1,k2.与x轴不重合的直线PQ过点E的充要条件是

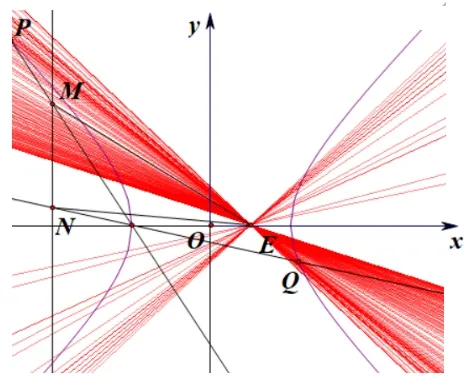
图2

结论3 的证明,有兴趣的读者可以参照结论2 的证明思路进行运算推理,在此不作过多的详细验证.

2.3 抛物线中的推广

结论4如图3,抛物线Γ:y2=2px(p＞0),O为坐标原点,点E(m,0)异于原点,P,Q是Γ 上的两点,直线OP,OQ与直线x=t分别交于点M,N,记直线ME,NE的斜率分别为k1,k2.直线PQ过点E的充要条件是

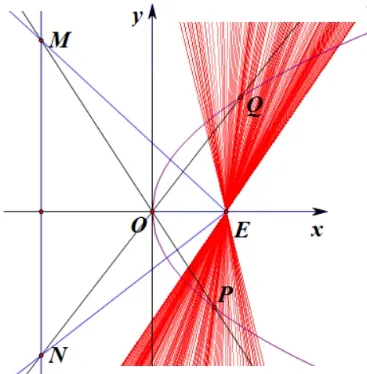
图3

证明首先证明必要性.设P(x1,y1),Q(x2,y2),直线l的方程为x=ny+m,将其与抛物线方程消去x可得y2-2npy-2mp=0,由题意直线与抛物线有两个交点,故Δ＞0,则

又直线OP,OQ方程分别为令x=t可得点因此

于是直线PQ的斜率为直线PQ的方程为

历经上述解析几何试题的探索,不难发现解析几何知识之间的联系是紧密的,教师要充分运用信息技术帮助学生养成敢于质疑,善于思考,理解概念、把握本质,数形结合、明晰算理,厘清知识的来龙去脉的良好数学学习习惯[1].解析几何教学,需要大胆猜想和小心求证的探索精神.深挖数学问题,拓展与延伸结论的一般性,才能更好的促进数学本质和数学通性通法的理解.期待通过类比、归纳、演绎等逻辑推理方式挖掘更多的解析几何精彩结论.