离散时间姿态互补滤波器及其参数整定研究∗

李 翔，王 涛

(桂林电子科技大学电子工程与自动化学院，广西 桂林 541004)

微机电系统(Micro-Electro-Mechanical System，MEMS)陀螺仪和加速度计具有体积小、成本低等显著优点，被广泛用于无人机等领域实现姿态测量[1－2]。为实现这两种传感器间的数据融合，一种普遍采用的解决方案是互补滤波(Complementary Filter，CF)算法。CF 的主要优势在于计算量小，适合于在计算能力有限的单片机上使用，且能达到与卡尔曼滤波(Kalman Filter，KF)相近的姿态估计精度[3－5]。然而，姿态测量领域目前所用的各种CF 算法存在如下两个不可忽视的问题。

第一个问题是各种CF 算法普遍基于连续时间架构，然而CF 算法在单片机或其他处理单元上实际是以离散时间的方式运行。尽管这种从连续时间到离散时间的转换可通过双线性变换等方法实现，但直接在离散时间条件下设计并实现CF 显然更为简便可靠。

第二个问题是CF 的参数整定。在姿态测量领域，针对加速度计测量值易受动态干扰的问题，出现了各种对CF 参数作自适应调节的算法[6－10]，以及对参数变化不敏感的CF 算法[11]等。然而此类自适应算法往往未能充分考虑传感器噪声及误差的统计特性，使得其参数调节缺乏严谨客观的依据。仅有极少数文献对传感器噪声频谱进行了实测，并据此进行CF 的参数整定[12]。

针对上述问题，本文提出了用于姿态估计的离散时间互补滤波(Discrete-Time Complementary Filter，DTCF)算法，推导了根据传感器噪声统计特性实现DTCF 参数整定的方法，通过仿真和实验验证了DTCF 用于姿态估计的有效性。

1 姿态测量及互补滤波原理

1.1 姿态测量

三轴加速度计可测量载体坐标系下的重力加速度矢量g＝(g1g2g3)T，由此即可利用反三角函数计算俯仰角θ与横滚角φ，分别如式(1)及式(2)所示[11，13]:

三维姿态的完整描述需要横滚、俯仰和航向这三个欧拉角，航向角的测量可借助三轴磁强计测量载体坐标系下的地磁场矢量h＝(h1h2h3)T来实现。航向角ψ的计算如式(3)所示[14－15]:

三轴陀螺仪可测量载体的角速度ω＝(ω1ω2ω3)T，进而可根据角速度测量值来推算姿态变化率[10]。将重力矢量和地磁矢量分别与角速度叉乘，即得它们对时间的导数，如式(4)所示:

1.2 互补滤波

传统CF 在频域实现数据融合。以姿态估计为例:由加速度计测量值解算的姿态xA采用具有低通特性的滤波器G(s)，以滤除噪声及动态干扰；对陀螺仪测量值积分得到的姿态xB则采用具有高通特性的滤波器[1－G(s)]，以抑制陀螺漂移引起的累积误差；由此可得CF 的s域传递函数，如式(5)所示。

Mahony 等[16]针对姿态估计问题，将传统CF 改造成具有闭环反馈结构的广义互补滤波器(Generalized Complementary Filter，GCF)，如图1 所示。GCF 的传递函数如式(6)所示，其中的G(s)若仅含比例环节，即G(s)＝KP，则为一阶互补滤波；若G(s)为比例与积分环节的结合，即G(s)＝KP＋KI×s－1，则构成二阶互补滤波。目前姿态估计领域所用CF算法大多以图1 所示GCF 架构为基础[17－20]。

图1 Mahony 型互补滤波框图

2 离散时间姿态互补滤波器设计

2.1 DTCF 算法原理

k时刻载体坐标系下的重力矢量既可直接由加速度计进行测量，也可由陀螺仪测得的角速度结合式(4)进行计算。将上述两途径进行加权融合，即构成本文的DTCF 算法，其具体步骤如下:

DTCF 第2 步:设k时刻加速度计测得的重力矢量为，按式(8)进行加权融合得到k时刻的重力矢量估计值，其中0≤G≤1 为加权系数，亦是DTCF 的唯一参数。

式(7)和式(8)所构成的DTCF 似乎只是在时域对加速度计和陀螺仪的测量值进行了简单的加权，但将它转换为z域形式即可看出其互补特性。在上述DTCF 中，待估计物理量x为重力矢量，加速度计给出的是x的直接测量值序列xA，k，而陀螺仪测量值代入式(7)所得到的则是x的增量序列ΔxB，k。又注意到z域中的差分算子可表示为(1－z－1)，故可得式(9)所示的z域表示式:

由式(9)可以看出，式(7)和式(8)构成的DTCF 算法在频域确实具有互补性，因而将其称为离散时间条件下的互补滤波器是恰当的。

2.2 DTCF 参数整定

DTCF 的参数G可根据方差最小化原则决定。在式(8)中，记协方差矩阵为Pk－1，Δgk协方差矩阵为Q，协方差矩阵为R，则的协方差矩阵Pk可由式(10)表示:

一般而言，传感器各轴的噪声大小近似相同且相互独立，则式(10)中各协方差矩阵可近似为标量矩阵(即各对角元大小相等且非对角元为零)，故可将式(10)改写为标量形式，如式(11)所示:

为使DTCF 保持稳定，应当有Pk－1＝Pk＝P为常数，故可得式(12):

为获得最佳滤波效果，应使P为极小，即令∂P/∂G＝0，且注意G为正数，由此解得

式中:Q和R可由实测数据统计得到。Q是由陀螺仪噪声及矢量更新算法所引起的误差，可由式(14)计算，其中:N为采样点个数，gr，k为k时刻重力矢量真值，Δgr，k为从(k－1)时刻到k时刻重力矢量真值的改变量，其余记号与式(7)和式(8)中一致。

另一方面，R反映加速度计的测量误差，可由式(15)计算:

值得注意的是，若记λ＝R/Q，则式(13)可改写为:

亦即DTCF 的参数整定结果实际是由Q和R的比值决定。

3 算法验证

3.1 半实物仿真

为验证上文所述DTCF 及其参数整定方法，采用荷兰Xsens 的MTi300 微型航姿模块采集两组姿态数据，分别记为数据集A 和数据集B，如图2所示。

图2 仿真所用姿态数据

仿真中，首先由图2 所示姿态数据生成加速度计和陀螺仪采样数据，两个数据集A 和B 各自对应的时间长度均为40 s，采样频率为20 Hz，故每一数据集中的采样点个数均为N＝800。由三维姿态得到载体坐标系下的重力矢量后进行归一化处理(即令重力矢量模长为1)，并加入标准差为0.1 的白噪声后得到加速度计测量值。另一方面，三维角速度加入标准差为0.005 rad/s 的白噪声以及随机游走误差后得到陀螺仪测量值。

生成加速度计及陀螺仪采样数据后，分别按式(14)和式(15)进行误差统计，得到方差Q和R，再按式(13)计算DTCF 的参数G，其结果列于表1。由表1 可见，两个数据集对应的DTCF 参数整定结果相互吻合得很好。

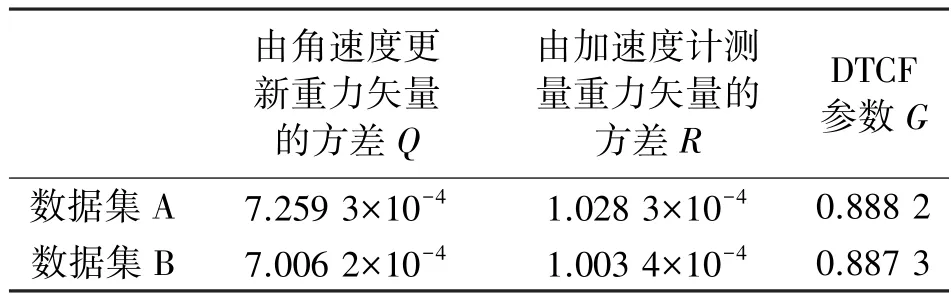
表1 误差统计及DTCF 参数整定结果

为进一步验证表1 所列DTCF 参数整定结果的可靠性，改变DTCF 的参数G取值，并观察其滤波效果随G取值的变化。图3 所示为两个数据集分别采用DTCF 进行姿态估计时，俯仰角与横滚角的均方根误差(Root-Mean-Square Error，RMSE)随参数G取值而变化的情况。由图3 可见，使俯仰角与横滚角的RMSE 达到最小的参数G取值确实与表1 所列参数整定结果非常接近。因此，本文所述DTCF 及其参数整定方法是可行的。

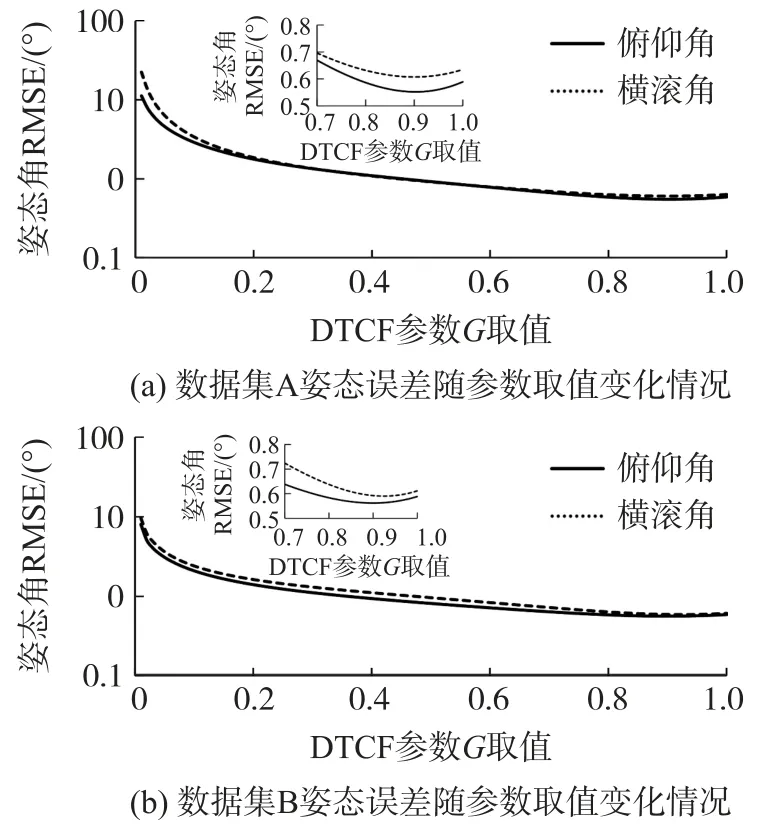
图3 DTCF 参数取值对姿态误差的影响

3.2 无人机飞行实验

采用基于开源飞控PIXHAWK2.4.8 的四旋翼无人机对本文提出的DTCF 算法作进一步测试，并与常用的扩展卡尔曼滤波(Extended Kalman Filter，EKF)[4]及GCF[3]算法进行对比。实验中，由PIXHAWK 的飞行日志文件中读取无人机姿态作为参考值，并分别采用EKF、GCF 和DTCF 三种滤波算法各自根据传感器测量数据估计姿态角。图4、图5和图6 依次为各算法的航向角、俯仰角、横滚角估计值与参考值对比情况。

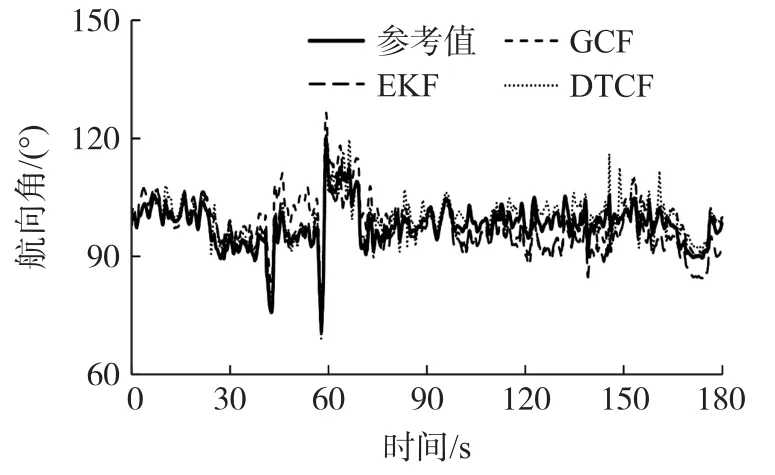
图4 不同滤波算法估计的航向角对比

图5 不同滤波算法估计的俯仰角对比

由图4～图6 可见，无人机飞行过程中姿态变化较剧烈，但在此种高动态条件下，EKF、GCF 以及DTCF 三种算法估计的姿态相差不大。对三种算法各自的均方根误差进行统计，结果如表2 所示，可见本文的DTCF 算法具有与EKF 和GCF 相当的姿态估计精度。

表2 三种滤波算法姿态误差对比

3.3 运行时间对比

采用基于增强型8051 内核的STC15W4K56S4单片机对上述三种算法(EKF、GCF 及本文的DTCF)的运行时间进行对比。STC15W4K56S4 单片机内部具有5 个16 位定时器，可分别记录EKF、GCF 和DTCF 三种算法各自的运行时间(以单片机的系统时钟周期为单位)。

图7 所示为传感器的每个采样周期中，以上三种算法在单片机上各自需要的时钟周期数的对比。此处所用的传感器原始数据来自上文所述无人机飞行实验，PIXHAWK 飞行日志文件记录时长为3 min，采样频率为10 Hz，故采样点个数N ＝1 800，即每种算法均进行了1800 次递推计算。对图7 所示各算法所需时钟周期数分别取平均值，再乘以单片机系统时钟频率的倒数，即得各算法在单片机上的平均耗时。在11.059 2 MHz 时钟频率下，上述三种算法的平均耗时如表3 所示。

表3 三种滤波算法耗时对比

由表3 可见，GCF 和DTCF 的运行时间均远低于EKF，这是由于EKF 涉及大量的矩阵运算。另一方面，DTCF 的运行时间又比GCF 减少了约一半，其原因在于DTCF 直接对重力和地磁矢量进行估计，而无需在这两个矢量和姿态四元数之间相互转换，从而比GCF 进一步降低了计算量。

3.4 讨论

GCF 的估计对象为姿态四元数，而四元数与重力矢量(或地磁矢量)间的关系是非线性的，这就使得其参数与传感器噪声特性间的关系变得复杂，故而在实践中往往直接采用试凑来进行参数调节。

DTCF 直接以重力矢量为估计对象，如2.2 节所述，DTCF 的参数可由方差Q和R的比值来确定，而这两个方差分别反映了获取姿态的两种途径(通过角速度积分推算姿态以及直接由重力矢量定姿)各自的误差大小。在实际应用中，方差Q和R可分别由式(14)和(15)统计得到，从而使DTCF 的参数选取充分反映传感器误差特性。3.1 节的仿真结果证明了2.2 节的理论推导与实际情况相吻合，从而为DTCF 参数整定提供了可靠依据。

对于需要输出完整三维姿态信息(即同时提供航向角、俯仰角、横滚角)的场合，由于姿态解算需同时用到重力矢量和地磁矢量，因而滤波器参数整定必须兼顾加速度计与磁强计各自的特性。对于GCF 而言，这将进一步增加其参数整定的难度。而DTCF 可以利用两个子滤波器分别估计重力矢量和地磁矢量，且这两个子滤波器的参数可相互独立地进行调节，从而能更好地分别适应加速度计及磁强计的噪声特性。

4 结论

本文提出的DTCF 可根据传感器噪声的统计特性直接确定其参数，为姿态估计所用的互补滤波器提供了新的设计思路。本文提出的DTCF 及其参数整定方法具有明确的理论基础和简便的实施步骤，达到了理论与实践的统一。实验表明，DTCF 的姿态估计精度与常用的EKF 及GCF 相近，但DTCF 具有更低的计算量及耗时，非常适合在计算能力有限的单片机上使用，有助于提高三维姿态估计的实时性。