重载铁路路堑边坡极限状态法稳定性分析研究
2023-11-29刘俊俊胡朋荣
曹 博 李 明 刘俊俊 胡朋荣
(中铁西安勘察设计研究院有限责任公司,西安 710054)
我国铁路工程领域的大部分设计以容许应力法作为计算结构设计安全性的理论方法,该方法将实际工程中的不确定性因素,统一用安全系数K 来评价设计的稳定性。
铁路线路穿越众多复杂地质区域,易形成不同类型的边坡。自然条件、地质环境的劣化,致使铁路路堑边坡灾害(溜坍、坍塌及滑坡)频发,对铁路的安全运营产生极大危害[1],也对铁路边坡的安全设计、整治加固设计提出了较为严格的要求。研究发现影响边坡设计稳定性的因素众多,例如:地震、降雨、人为、车载等,且以上因素都具有随机性。TB 10001-2016《铁路路基设计规范》的边坡安全系数,是在长期经验积累中形成的一种评判边坡设计稳定性的标准数值。众多研究表明,边坡灾害大都具有随机变异性,用单一的经验数值去评定其稳定性已不适应铁路的设计趋势[2-4]。Q/CR 9127-2018《铁路路基设计规范(极限状态法)》的颁布,标志着铁路行业的边坡设计从容许应力法向极限状态法的转变。该规范将极限状态理论引入到铁路路基设计中[5-6]。极限状态法是一种概率论的方法,该方法将影响因素随机抽样化,然后进行多种组合得出边坡的设计稳定性,极限状态法更符合实际情况。专家学者基于铁路的边坡设计,对比研究了容许应力法和极限状态法的差异,统一认为极限状态法的经济性、合理性更好,公式的分项系数更接近实际工程[7-9]。建筑、公路及水利行业等领域的极限状态法的规范相对出版较早、比较完善,是一半概率或概率性的一种极限状态[10]。
基于此,本文在极限状态理论和Q/CR 9127-2018《铁路路基设计规范(极限状态法)》的基础上,以朔黄铁路龙宫站区的典型路堑边坡为实例,利用极限状态法计算了该路堑边坡的可靠指标和失效概率,同时采用一般分离法计算了重载铁路下岩土边坡的各类分项系数,并为解决重载铁路在边坡稳定性分析方面提出了有利的指导建议。
1 极限状态理论(可靠度理论)
概率极限状态设计法是以概率理论为基础,将荷载效应和影响结构抗力的主要因数视为随机变量,通过统计分析确定可靠概率来度量结构可靠度的结构设计方法[11-12]。在边坡工程设计中,可靠度分析已被众多学者所接受,通过建立不确定模型对边坡稳定性能进行评估。这种评估方法采用了可靠度和失效概率。将衡量工程结构可靠的计算方法归结于岩土工程和概率论相结合的产物[13]。
结构概率极限状态的分项系数设计,从方法上讲,将经典的概率论、数理统计与先进的计算技术和结构的分析方法融为一体,形成一套严密、科学的设计体系,促进运用统计数学来处理工程结构的设计问题;从理论上讲,该设计理论摒弃了以往的定值设计概念,使结构设计理论第一次真正地由确定性设计走向不确定性设计,较全面地考虑影响结构可靠性诸因素的客观变异性,实现了运用概率理论来度量结构的可靠度,使所设计的结构具有明确的可靠含义。
结构构件承载能力的极限状态可表达为式(1),随着抗力效应和作用效力的概率统计和随机组合,得到完成设计的可靠性,将其称之为可靠概率Ps,Ps+Pf=1。
式中:R——结构的抗力效应;
S——作用效力;
Z——功能函数。
根据Z 值的大小,边坡的状态可划分为以下3 种:
(1)Z <0,即R <S,边坡处于破坏状态。
(2)Z=0,即R=S,边坡处于极限状态。
(3)Z >0,即R >S,边坡处于安全状态。
失效概率和可靠概率关系如图1所示。

图1 失效概率与可靠概率关系图
铁路工程结构可靠指标计算可根据结构极限状态方程和随机变量的特征,常用的方法有蒙特卡洛模拟法、一次二阶矩法、JC 法、响应面法[14-15],必要时需要考虑随机变量的相关性对结构可靠指标计算值的影响。结构的分项系数是指为保证所设计的结构具有规定的可靠度而在设计表达式中采用的系数,它根据有关基本变量的概率分布类型和统计参数及规定的可靠指标。通过大量的迭代计算并结合工程经验,分为抗力分项系数和荷载分项系数两类。
根据Q/CR 9127-2018《铁路路基设计规范(极限状态法)》中对路堑边坡的规定,当采用圆弧滑动法进行边坡稳定性分析计算时,持久设计状况下应符合式(2):
引入极限状态理论中的功能函数Z,高路堑边坡的功能函数表达式为:
式中:γ1、γ2——抗力效应分项系数;
γ3——作用效应分项系数;
Sd——持久设计状况下路堑边坡滑动作用效应设计值;
Rd——持久设计状况下路堑边坡滑动抗力设计值;
Wi——土条i 重力标准值;
θi——土条i 的底面法向力与铅直轴的夹角;
ci——土条i 的土体黏聚力标准值;
li——土条i 的底边长度;
φi——土条i 的土体内摩擦角标准值。
分项系数是一种为保证所设计的结构或构件具有规定的可靠指标,在结构极限状态设计表达式中作用和抗力所采用的取值系数。分离函数是将安全系数与可靠指标联系起来,并把安全系数加以分离,使其表达为分项系数的形式。
目前常用的分项系数方法为一般分离法。通过一定的数学变换,定义分离函数Φi,然后进行分离。该方法适用范围广,不仅可用于2 个变量的情况,而且容易推广到多个非正态变量的情况[16-17]。
采用一般分离法对式(4)~式(6)进行分析,得出相应的分离函数Φ:
式中:Φ1、Φ2和Φ3——cili、Wicosθitanφi、Wisinθi的分离函数;
σ1、σ2和σ3——cili、Wicosθitanφi、Wisinθi的标准差;
δ1、δ2和δ3——cili、Wicosθitanφi、Wisinθi的变异系数;
β——结构的可靠度,根据分离法得出边坡作用效应和抗力效应的分项系数。
2 工程案例
为研究山区重载铁路下路堑边坡在不同工况下的极限状态和抗力、作用分项系数的取值,以朔黄铁路龙宫站区的高路堑边坡为例,讨论其边坡稳定性和分项系数取值。朔黄铁路是我国首开2 万t 级的重载运营铁路,为国家Ⅰ级干线双线重载电气化铁路,所穿地区地质条件复杂,山区地势崎岖,属典型山区铁路。选用该铁路龙宫站的高路堑边坡。
根据国家地震局GB 18306-2015《中国地震动参数区划图》,地震动峰值加速度为0.15 g(地震基本烈度为Ⅶ度),地震动反应谱特征周期为0.40 s。
根据现场勘察和室内土工实验结果,绘制该铁路路堑边坡的土体强度参数,如表1所示。
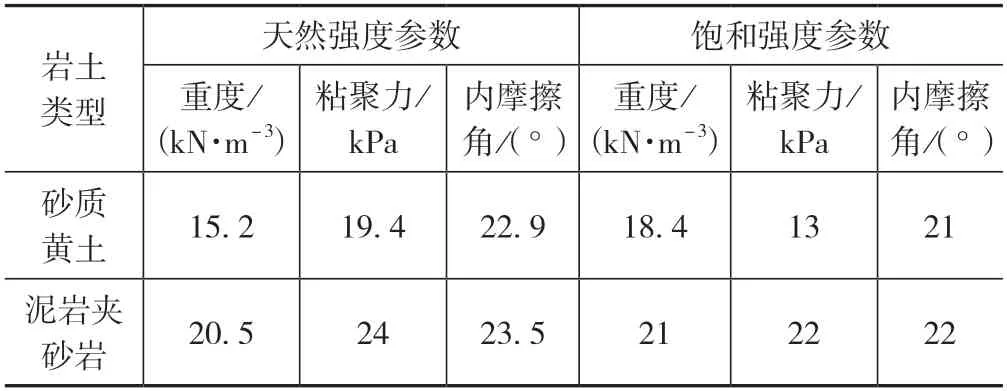
表1 岩土体强度指标统计表
3 极限状态研究
3.1 边坡稳定性分析
不同因素对边坡的稳定性的影响存在差异,对于特殊边坡,其稳定性的要求更为严格。本文以摩根斯坦法进行边坡稳定性分析,同时采用蒙特卡洛法对边坡的土性参数(如内摩擦角、粘聚力和重度等)进行随机抽样和组合,搜索边坡的最危险潜在滑动面,计算边坡极限状态下的稳定性、可靠度、平均安全系数和失效概率[18]。李萍[19]等人分析了土性参数分布类型对边坡稳性的影响,认为粘聚力和内摩擦角服从正态分布、重度对边坡稳定性的影响较小,可忽略不计。因此,在分析计算中,采用正态分布类型将3 种不同工况的模型进行计算,如图2所示。

图2 不同工况下铁路路堑边坡极限状态及受力图
不同的失效概率所得的分项系数也不一样,理论极限状态(即Z=R-S=0 时的状态)在可靠指标和失效概率的对应关系下,可靠指标β趋于0,边坡的失效概率趋于50%。一旦超越这个失稳临界点,边坡稳定性都会有不同程度的变化。
自重条件下,路堑边坡的稳定系数为1.13,失效概率为38.24%;自重+地震条件下,路堑边坡的稳定系数为0.982,失效概率为55.88%;自重+暴雨条件下,路堑边坡的稳定系数为0.941,失效概率为64.71%。根据铁路路基设计规范,在评估边坡稳定性时,应满足以下规定:一般工况下边坡的最小稳定安全系数应为1.15~1.25;地震工况下边坡的最小安全系数应为1.10~1.15。该工程在正常状态下,有38.24%的概率形成滑坡。根据条分法将边坡分成34 个条块,并将不同条块的抗力效应和作用效应绘制成图,如图3所示。

图3 边坡不同条块力学性能图
由图3 可知,自重条件下,坡体中部作用效应S >抗力效应R,因此是易发生滑坡的部位;自重+地震条件下,坡体顶部以及中部同样都易发生滑动;自重+暴雨条件下,坡体顶部及中部会发生滑动,特别是坡体中部的条块,其抗力效应R 远小于作用效应S。
对滑体条块进行力学分析,发现朔黄铁路龙宫站区铁路边坡的稳定性分析中,当超过边坡的极限状态(Pf>50%)时,坡体顶部和中部更易发生滑动,最低滑坡处位于坡高h 的0.47 倍处。
通过工程实例、数值模拟等手段,发现该地区的坡体都存在潜在滑移的可能,且滑坡形成位置主要位于岩土界面(坡高的0.47 倍处)。针对这一计算结果,朔黄铁路在龙宫站区路堑边坡治理时,以坡高的0.47 倍为治理方案的依据,对该地区边坡治理提供了极大的帮助。同时,通过多次搜索的最危险的潜在滑面、失效概率、滑移方量等结果,为工程治理提供了指导。
3.2 分项系数研究
分项系数是根据基本变量的概率分布类型和统计参数,通过计算分析并结合工程经验优化确定的。根据实际工程案例的数值模拟计算得到的可靠指标和一般分离法计算所得分项系数,将极限状态理论、铁路路基设计规范(极限状态法)以及理论极限状态等3 种分项系数的计算绘制,如表2所示。

表2 山区重载铁路路堑边坡分项系数统计表
由表2 可知,相较于土质边坡,山区铁路[20]的高路堑边坡自身就存在潜在滑动面(岩土分界面),在暴雨、地震的作用下,岩土界面更容易产生滑动面,相较于铁路路基设计规范中的一般边坡,其安全系数相对较小。
山区重载铁路在自重条件下所得抗力和作用效力均小于铁路路基设计规范中规定的分项系数取值;极限状态下,边坡的失效概率为50%,即Z=R-S=0,且可靠指标在此处为0;根据分项系数计算方法,极限状态下此下滑力和抗滑力的分项系数取值均为1.0。自重+地震、自重+暴雨条件下,该路堑边坡超出极限状态,其各分项系数均小于1.0。Q/CR 9127-2018《铁路路基设计规范(极限状态法)》中未确定这种特殊工况下的边坡进行分项系数。极限状态法得出自重+地震、自重+暴雨的各分系数取值约为0.9。因雨水渗入土体,增加了原土体重量,因此应提升与土体质量有关的抗力,从而降低分项系数。
自重+暴雨条件下,∑ Wisinθi项增加较剧烈,土体的抗剪强度降低,边坡失效概率下降10%,∑Wisinθi的分项系数降低0.1~0.2,呈急剧下降状态。
针对该工况的两种特殊工况,分项系数取值的普适性还需进行多次验证和统计分析。
4 结论
以朔黄铁路龙宫站区高路堑边坡为例,采用极限状态法和数理统计相结合的方法,计算了自重工况、自重+地震工况及自重+暴雨工况下的边坡极限状态,得到主要结论如下:
(1)该路堑边坡超出极限状态,即Pf>50%时,最低滑坡处位于坡高h 的0.47 倍处。
(2)各分项系数取值均小于铁路路基设计规范中规定取值。为提高结构的目标可靠指标,需在设计支护结构中进行调整。
(3)边坡自重+暴雨条件下,∑Wisinθi项增加剧烈,边坡失效概率下降10%,因此∑Wisinθi的分项系数会降低0.1~0.2。
(4)研究成果可为山区重载铁路路堑边坡稳定性分析设计提供一定的借鉴。
