AT供电方式下直接供电分支接触网的故障测距方案
2023-11-29林国松吴泽方杜欧洋朱志龙
洪 彬 林国松 吴泽方 杜欧洋 朱志龙
(1.西南交通大学,成都 610031;2.中国铁路广州局集团有限公司,广州 518001)
AT(Auto Transformer)供电方式的供电系统电压稳定、供电能力强,在我国重载铁路和高速铁路中得到广泛应用[1]。接触网不仅有电连接还有机械连接,是牵引供电系统较为薄弱的环节,接触网的稳定影响着整条线路的运行。当故障发生后,接触网故障测距是快速发现并排除故障的重要技术保障。
在一些特殊供电区段(如正线间的联络线、变电所上网点、站场和电力机车整备线等),为了节约建设成本或方便维护,通常在邻近的正线供电区间上“T”接出分支直接供电线路,以获取电能。随着AT供电方式在我国的广泛应用,以AT供电方式牵引网“T”接出直接供电分支线路(以下简称“支线”)的牵引网结构逐渐增多。由于在支线上并未安装断路器及保护设备,当分支线路发生故障时,既有故障测距装置无法提供准确的故障距离,进而导致故障排除和供电恢复延缓,影响铁路的运输速度和效率。
文献[2-4]说明了AT供电方式下的故障测距原理、方法及其适用范围;文献[5-6]介绍了复线直接供电方式下的故障测距方法和应用效果。然而,既有的故障测距装置或系统无法实现对AT 牵引网带直供支线的故障测距。文献[7]推导了AT 加直供越区供电方式下的阻抗分布;文献[8]介绍了全并联AT 越区供电方式下不同区段的故障测距方法;文献[9-11]介绍了站场等含有众多分支线路的接触网,通过在分支点处安装电流测量装置,检测电流突变增量,从而判断支线故障。然而,该装置只有对同一股道多组安装,才可实现对分支线路的故障区分。文献[12]利用小波神经网络拟合行波特征值与故障之间的关系,实现故障测距;文献[13]采用行波法对AT供电方式下的多分支接触网进行故障测距,通过在分支线路正馈线增设流互,借助电流方向来区分正线以及支线故障。
本文以AT供电方式下直接供电分支牵引网为研究对象,分析了传统吸上电流比和电抗距离表法在应用中的局限性。在不增加硬件设备的前提上,提出了一种综合吸上电流和电抗法的故障测距方案,实现了直接供电分支接触网的故障测距功能。
1 AT供电方式的直接供电分支接触网及其电路分析
1.1 AT供电方式下直接供电分支接触网
典型的单线AT供电方式和直接供电分支接触网如图1所示,SS、ATP 和SP 分别为牵引变电所、AT 所和分区所,牵引变电所至AT所区段为第AT1段,AT所至分区所为AT2 段。AT1 段存在分支点T0,从AT 牵引网的接触网分支点T0 到末端的T1、轨道分支点R0到末端R1 的线路为支线。E 是牵引变电所等效电源,T、R 和F 分别为接触网、钢轨和正馈线。

图1 AT供电方式下直接供电分支牵引网图
AT供电方式牵引网故障分T-R 型、F-R 型和T-F 型故障,直接供电方式牵引网没有F 线,当直供支线接触网发生故障时,只存在T-R 型短路故障,且支线牵引网电流必然全部流经分支点。由图1 列出电压回路方程:
式中:D1——AT1 段线路长度(km);
D2——AT2 段线路长度(km);
l1——支线上网点到牵引变电所的距离(km);
l2——支线上的短路故障到分支上网点的距离(km);
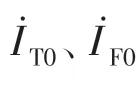
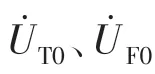
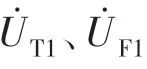
ZT——AT 线路接触网单位自阻抗(Ω/km);
ZR——AT 线路钢轨单位自阻抗(Ω/km);
ZF——AT 线路正馈线单位自阻抗(Ω/km);
ZTF——AT 线路接触网与正馈线间的单位互阻抗(Ω/km);
ZFR——AT 线路钢轨和正馈线间的单位互阻抗(Ω/km);
ZTR——AT 线路接触网和钢轨间的单位互阻抗(Ω/km);
ZT1——支线接触网单位自阻抗(Ω/km);
ZR1——支线钢轨单位自阻抗(Ω/km);
ZT1R1——支线接触网和钢轨间的单位互阻抗(Ω/km)。
根据基尔霍夫电流定律,得:
式中:IT1——变电所流向分支点T0 的T 线电流;
IR0——变电所流向分支点T0 的钢轨电流;
IR1——分支点T0 流向正线钢轨的电流。
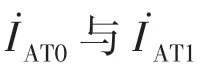
式中:IAT0——变电所的吸上电流;
IAT1——AT 所的吸上电流。
根据式(4)推导出分支上网点处吸上电流比为:
式中:Qx1——分支上网点的吸上电流比。
随着故障点在AT1 段距离的变化,得到该AT 段的电流比距离关系[14]:
式中:D——故障AT 段长度(km);
l——远离牵引变电所方向上,距故障AT 段始端的距离(km)。
变电所测得的吸上电流与故障距离呈线性关系[15]。
1.2 直接供电分支牵引网短路阻抗计算
牵引变电所馈线阻抗计算[16]公式为:
根据式(7)可计算出AT1 段分支上网点处发生T-R 故障时,牵引变电所测得的短路阻抗为:
式中:ZAT(l1)——分支上网点发生短路故障的短路阻抗;
Rg——短路点接触电阻。
当支线上发生短路故障时,在牵引变电所测得的短路阻抗为:
式中:ZD——支线发生短路故障的短路阻抗。
根据式(8)可得到发生在分支上网点处的短路故障电抗:
式中:XAT(l1)——支线上网点发生短路故障的短路电抗。
根据式(9)可得到故障发生在支线时的短路电抗:
式中:XD——支线发生短路故障的短路电抗;
XAT(x1)——变电所到支线上网点的电抗;
XT1——T 线的自电抗;
XR1——钢轨的自电抗;
XT1R1——T 线和钢轨路的互电抗。
根据式(10)、式(11)可以得出AT 线路发生T-R短路故障以及当支线短路故障时电抗随距离的曲线,如图2所示。当AT供电方式下发生T-R 短路故障时,短路电抗和距离呈非线性关系。当支线发生短路故障时,支线的短路电抗和距离呈线性增长关系,符合直供线路的短路阻抗特性。
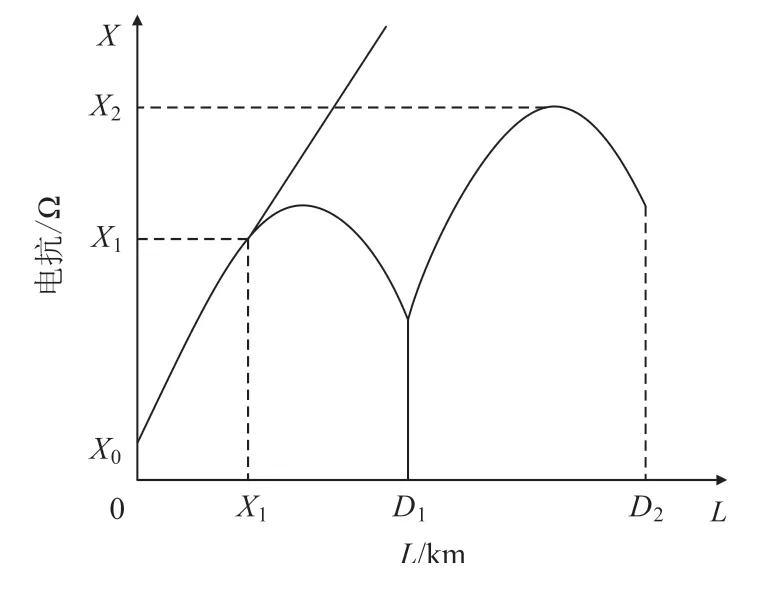
图2 短路电抗与故障距离曲线图
2 AT供电方式下直供分支接触网故障测距方法
2.1 AT供电方式下直接供电分支接触网故障测距的局限性
当单线AT供电方式牵引网发生T-R、F-R型故障,通常采用吸上电流比法;对于T-F 型故障,则采用电抗距离表法。吸上电流比会受站场、大地泄漏、AT 漏抗等因素的影响,因此在程序设计中不采用整个AT 段直线测距公式,而采用分段线性法。直接供电方式下,单线时采用电抗法(电抗距离表),复线时采用上下行电流比法。
根据式(5),当支线上任一点发生短路故障时,牵引变电所测得的吸上电流比为固定值,且吸上电流比值的大小与在AT1 段分支上网点处发生TR 短路故障时相等。采用吸上电流比法只能将故障大致定位到分支上网点附近,无法对支线短路故障进行精确定位。
由图2 可知,若采用电抗法测距原理对AT 供电带支线接触网进行测距,会导致线路中出现同一电抗值对应多个故障距离的情况,故无法对AT 供电正线和直接供电支线上发生短路故障进行区分。
2.2 AT 正线与直供支线的判别
根据式(5),当支线发生短路故障时,与正线在分支上网点处发生T-R 型短路故障相比,在牵引变电所处测得的吸上电流比值相同,从而故障发生在支线的判据为:
式中:ΔQ——吸上电流比值差;
Q——牵引变电所在故障发生在AT1 段时的吸上电流比;
Qset——按AT1 段分支点接触网故障时的吸上电流比的整定值;
ΔQset——比值差整定值。
支线接触网沿线各处故障,按避免在牵引变电所得到的吸上电流比因系统误差引起的最大波动值来整定。也就是说,满足式(12)的故障点将被认为故障发生在支线上,这样会导致当故障发生在分支点附近的正线上时,误判为故障发生在支线上。在此,假设ΔQset取0.015,该值的意义为如果AT 段长15 km,吸上电流比的范围为0~1,比值差为0.015 导致正线牵引网故障被误判为支线故障的测距误差约为15 000 m×0.015=225 m,这完全满足企业标准对故障测距误差小于500 m 的精度要求。在实际应用中,可以在支线进行多点短路试验或机车负荷试验[17],以确定该电流比偏差整定值。
2.3 直供支线故障测距
支线故障时,在牵引变电所测得的短路电抗与故障距离呈线性增长的一一对应关系,此时可以采用电抗-距离查表法进行故障测距。AT供电方式下的直接供电线路故障测距方法流程如图3所示。
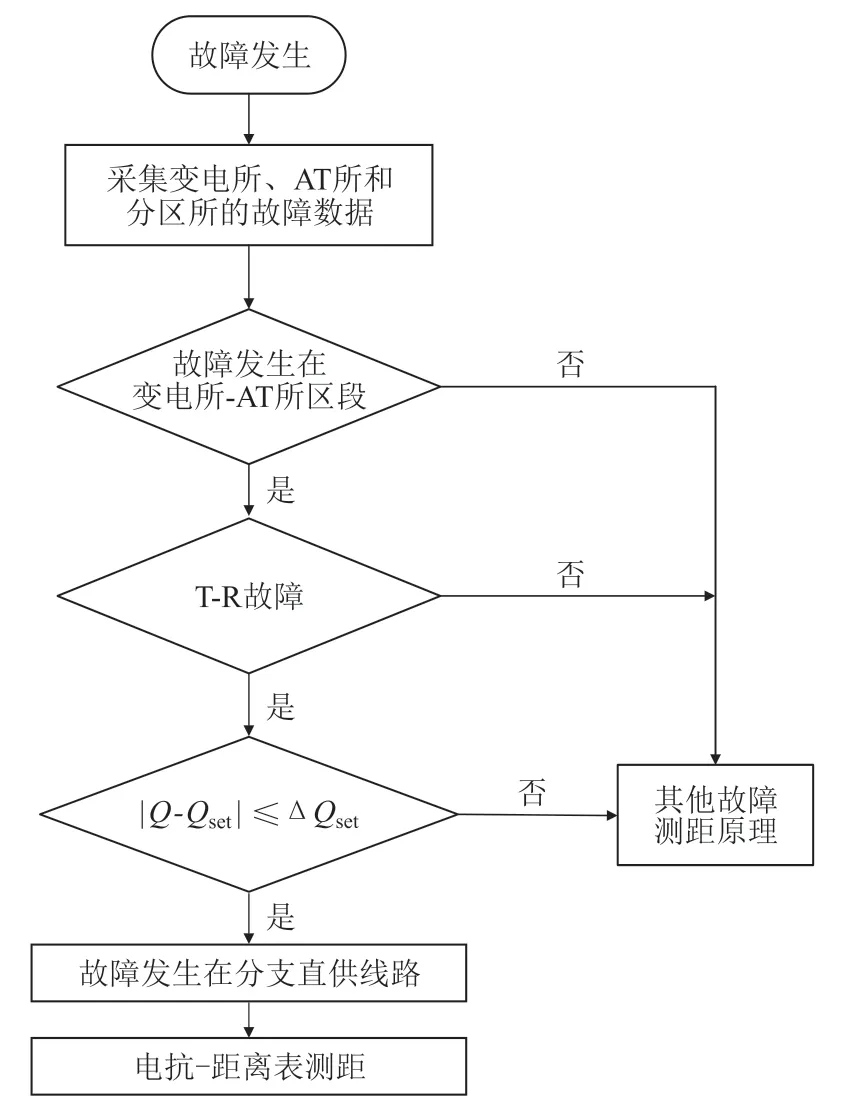
图3 AT供电方式下直供支线故障测距流程图
无论采用单线或复线全并联AT供电方式,每个供电段包含几个AT 段,在含有直接供电分支线路的AT 段,可采用类似的测距方法。
3 仿真验证
搭建单线AT供电方式带直供支线的仿真模型,模型参数如表1所示。其中,牵引网AT1 段长15 km,AT2 段长10 km,直供支线长6 km,在AT1 段距牵引变电所10 km 处T 接上网。

表1 AT供电方式下带直供支线仿真模型参数表
AT 线路牵引网单位阻抗矩阵为:
直供支线T 线单位自阻抗、R 线单位自阻抗和接触网-钢轨间的单位互阻抗分别为:0.145 + j 0.55、0.084 + j 0.407、0.05 + j 0.314。
仿真得到正线和直供支线发生T-R 故障时吸上电流比与距离的关系如图4所示。由图4 可知,正线牵引网上发生短路故障时的吸上电流比与距离呈线性增长的一一对应关系,支线(含分支点)上任意一点发生短路故障时,牵引变电所测得的吸上电流比值为固定不变的0.591。

图4 正线和支线T-R 故障时吸上电流比-距离关系曲线图
直供分支上网点处发生短路故障时的吸上电流比值为0.591,在其±0.015 范围内正线上的测距结果如表2所示。按式(12)的测距最大误差为322 m,满足故障测距的精度要求。

表2 AT 供电带直供支线测距误差表
正线和直供支线发生T-R 故障时变电所测量的短路电抗-距离曲线如图5所示,短路电抗与距离呈线性增长关系,支线上的起始电抗与正线分支上网点处T-R 短路电抗相同,可采用电抗法测距原理对直供支线进行故障测距。

图5 正线和支线T-R 故障时短路电抗-距离关系曲线图
仿真结果表明,首先可以通过固定的电流比整定值确定故障发生在分支点附近或支线上,再根据支线的短路电抗-距离关系计算实际故障距离。
4 现场实例验证
汉龙变电所至李朗分区所正线采用复线AT供电方式,李朗线路所至平湖南支线采用直接供电方式。杭深铁路汉龙变电所至李朗分区所供电示意如图6所示,具体线路距离参数如表3所示。

表3 汉龙变电所至李朗分区所线路距离参数表
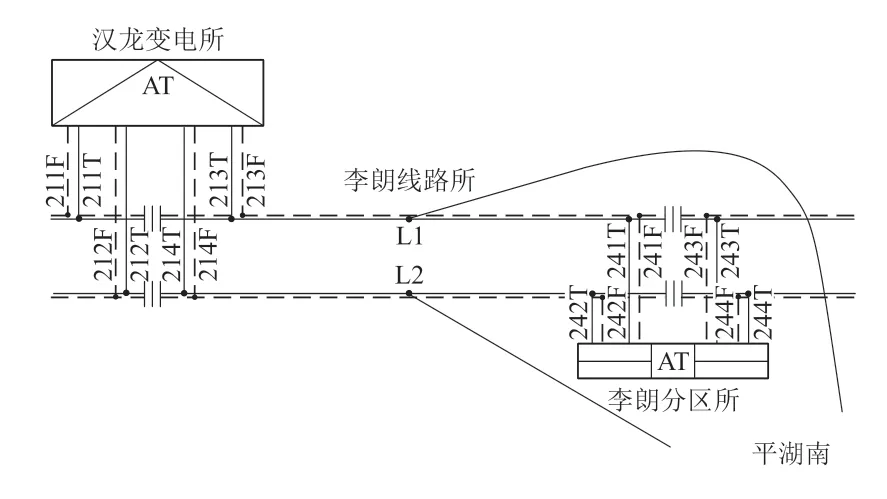
图6 汉龙变电所至李朗分区所供电示意图
以213 下行馈线为例,2014—2021年,下行支线L1 发生短路故障引起牵引变电所跳闸共计6 起,故障数据如表4所示。
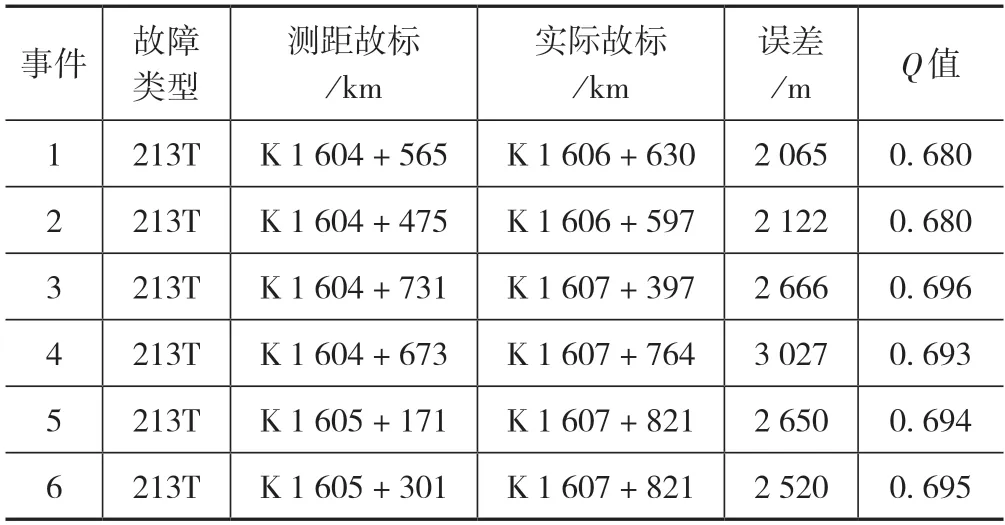
表4 支线L1 短路故障数据表
由表4 可知,故障测距误差远大于企业标准对故障测距精度的要求,这增加了故障排查和线路恢复供电的难度与耗时。
在牵引变电所测得Q 值在很小的范围变动,因此可以取(0.696+0.680)/2= 0.688 为分支点及支线故障的基准值,以0.01 为ΔQset整定值。由表3 可知,直供支线分支点所在AT 段正线长12.9 km,根据最大ΔQ值造成的最大测距误差为12.9×0.01=129 m,这满足企业标准对故障测距精度的要求,也验证了式(5)推导的正确性和对式(12)中确定ΔQset整定值原则的合理性。因此,通过式(12)可以实现故障发生在正线和支线上的区分。
5 结论
本文通过对AT 供电带直接供电分支线路进行分析,提出了一种综合AT 吸上电流比法和电抗距离表法的故障测距方法。首先通过吸上电流比法实现对正线和支线的区分,再通过电抗距离查表法实现对支线的故障测距。根据已有线路所发生的历史故障数据进行分析,验证了采用实测吸上电流与分支点吸上电流比近似的方法实现对正线和支线的区分的可行性。通过数值仿真验证了该方法的可行性、准确性。该方法不需要在接触网增加任何测量装置,仅通过改进既有故障测距系统程序即可实现。此外,该方法对现场该类供电方式提供了有益的参考。未来考虑站场和“T”接供电导致线路参数不均匀的情况,对Q 值做进一步的修订,从而提高故障测距的精度。
