基于点安全系数的边坡加固优化设计研究
2023-11-29刘剑光
刘剑光
(中铁二院工程集团有限责任公司,成都 610031)
随着我国交通建设的快速发展,大量工程项目和基础设施建成的同时,工程边坡问题也日益突出[1]。如何对这些边坡进行有效的加固成为热门的研究课题[2]。
现有方法大多通过各种极限平衡分析法来计算边坡的滑坡推力分布[3-4],并在边坡的下部设置抗滑桩。这样的设计方法虽然能对边坡做到较好地加固作用,但是往往会造成经济损失。这是因为边坡上覆土层的坡度和厚度在不同的部位存在差异,导致潜在滑面上的应力状态也具有差异性,即潜在滑面上各点的安全储备不同。闫玉平[5]提出根据强度将滑带分成不同的区域,分别进行抗剪强度的计算,充分考虑了滑带土体的峰值强度与残余强度的差异性,该方法得到的滑坡推力更加符合真实情况。李海涛[6]通过有限差分软件FLAC3D 研究了川北基坑高边坡的加固方案。侯超群[7]通过上限定理研究分析多级抗滑桩对有抗震要求的边坡加固方案,获得了最佳的抗滑桩加固方案。上述方法在一定程度上考虑了边坡的安全状况,但步骤繁琐,可能会影响施工速度。因此,需要提出一种能够综合考虑边坡区域安全的加固方案设计方法。
本文通过分析边坡的点安全系数分布情况,直观地得到边坡不同区域的安全状况,在点安全系数较小的区域布设抗滑桩进行加固,并通过有限差分软件FLAC3D 软件进行了对比验证。
1 点安全系数定义
杨涛[8]等根据摩尔-库仑强度准则将某一个单元体的抗剪强度与沿着滑面方向的剪应力的比值定义为点安全系数,表达为式(1):
式中:FF——点安全系数;
τu——单元的抗剪强度;
c、φ——土体的黏聚力和内摩擦角;
σn、τ——计算点的正应力以及滑动方向上的剪应力。
当一个单元的点安全系数等于1.0 时,说明该点处于极限平衡状态,若集中的大范围土体单元点安全系数小于或等于1.0,则说明该区域土体已经达到极限平衡状态,有较高的失稳风险。
由于空间应力为二阶张量,剪切面的方向是不确定的,这会导致点安全系数的具体值不唯一。真实的边坡局部稳定性指标,应是最危险剪切面上的计算值,也就是点安全系数的最小值。因此需要对式(1)求出极值,找出最小点安全系数及其所对应的最危险的截面[9-10]。
通过数学软件MATLAB 对该最小值进行求解,推导出最小点安全系数。
首先根据弹性力学空间问题公式:
式中:l、m 和n——斜面外法线与应力主项的方向余弦;
σ1、σ3——最大主应力和最小主应力;
σ2——中主应力。
将式(2)弹性力学空间问题公式代入到式(1)中可得到点安全系数的表达式:
点安全系数表达式是一个关于m 和n 的二元函数。在数学软件MATLAB 中进行求解极值,首先求解出一阶偏导方程组,得到4 个驻点,然后代入二阶偏导中判断是极大值点还是极小值点,最后得到最小点安全系数公式:
式中:FFmin——最小点安全系数。
最小点安全系数对应的最危险截面方向角(最危险截面法线方向与最大主应力的夹角)应满足[11]:
式中:α——最危险截面方向角。
由此可得到更加符合实际情况的最小剪切面所对应的点安全系数。将推导所得的最小点安全系数公式使用FLAC3D 的FISH 语言进行编程,能够得到计算模型所有区域的最小点安全系数值。
2 工程概况
2.1 地形地貌
西南地区某桥梁桥址区微地貌为河谷地貌,区域内河谷、盆地、山地相间分布。地势为北高南低,西高东低,且海拔高差悬殊大。斜坡地形陡倾,植被茂密,自然坡度为20°~35°,局部切坡段可达40°。地势从北向南总体上呈高中山峡谷地形。斜坡上土层厚度较大,属于典型的二元结构边坡,桥址区内未见基岩露头。
2.2 地层岩性
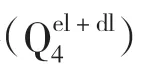
桥梁基础位于中部稍缓平台处,地表覆盖土层厚4.8~8.5 m,为粉质黏土,呈灰黄色,可塑状,干强度中等,韧性中等,含18%~26%碎石,无摇振反应。下伏基岩主要为变粒岩,灰色,细粒状变晶结构,片状构造,主要由石英和长石组成。岩芯呈短柱状、少量柱状。桥梁基础处于粉质黏土中,桩基承台下的地基土相对基岩的承载力及稳定性较差,但基本可满足承台基础的承载力要求。上覆粉质黏土在自然状态下处于稳定状态;但在开挖、降雨、地震等极端情况时,特别是下方边坡表土层滑走后而形成临空面,可能出现部分失稳,对桥梁长远期稳定产生不利影响。
根据钻探、物探成果,钻孔均未揭露出地下水,但桥梁基础位置地形较为平缓,上部为斜坡。从地形上来看,存在上部斜坡雨季汇排至平缓平台的可能。因此,要注意雨季期间降雨时,受降雨下渗补给,加之地表土层及全风化较厚、较松散,部分地表径流易下渗松散土层及浅部基岩裂隙中,故雨季时地表松散孔隙水有所增大、浅部较破碎岩层中的基岩裂隙水较旱季时有所增加。此时可加强地表截排水,以减少雨季时地表径流下渗,并防止对桩基承台的不利影响。
3 二元结构边坡模型及其参数
西南地区某桥梁基础架设于土-岩二元结构边坡之上,坡体上覆粉质黏土,厚度4.80~15.30 m,下部为基岩。根据坡面高程点坐标信息和地质调查结果,综合建立了其地质三维模型。模型高600 m,长1 100 m,宽200 m。模型边界条件为四周节点施加法向约束,底面节点施加固定约束。模型网格划分采用四面体单元模型,模型单元总数为60 743 个。本构模型采用Mohr-Coulomb 弹塑性本构模型,桩基础和承台采用结构单元模拟(Pile 单元和Shell 单元),土-岩分界面则采用接触面单元模拟。FLAC3D 提供了以库仑滑动和/或拉伸和剪切结合为特征的接触面单元。
岩土工程中涉及到很多的接触问题,例如土体沿着土-岩界面的滑动、挡墙与墙后填土之间的接触、土石坝中混凝土防渗墙与土体之间的接触等。接触面单元可以分析一定受力条件下2 个接触的表面上产生错动滑移、分开与闭合,故适合用于解决这一类问题。由接触面单元组成的界面具有摩擦、内聚、膨胀、法向和剪切刚度以及拉伸和剪切结合强度等特性,适用于模拟各种岩土界面。岩土参数取值如表1所示。
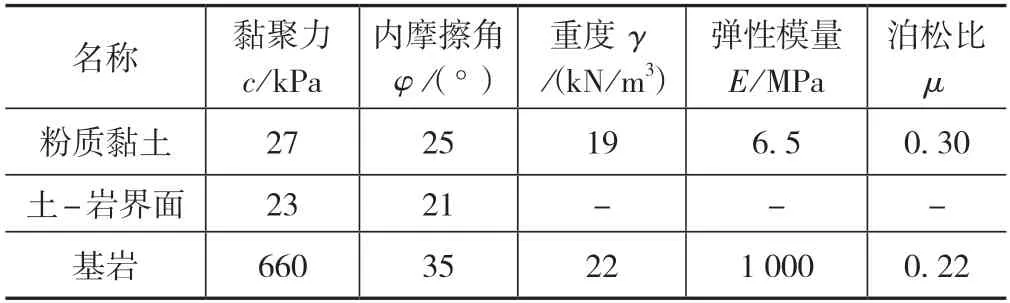
表1 岩土参数取值表
4 土-岩界面点安全系数分布
二元边坡的破坏模式通常为上覆土层沿土-岩界面或风化层界面发生滑动[12],故分析土-岩界面的点安全系数分布情况可以有效评价二元边坡的局部稳定性,对桥梁基础、隧道洞口等工程的选址具有指导意义,也可为加固位置的选择提供充分依据,进一步进行加固优化。土-岩界面点安全系数的计算过程如下:
(1)首先计算边坡自重条件下的应力状态,获取边坡的初始应力场。
(2)根据土-岩界面上的应力状态,通过FISH 语言自编程,提取边坡土-岩界面上各单元的应力值,计算求取点安全系数的分布情况。自然状态下土-岩界面点安全系数分布如图1所示。
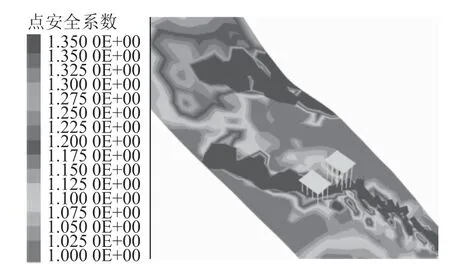
图1 自然状态下土-岩界面点安全系数分布图
分析土-岩界面点安全系数分布结果可知,该边坡桥梁基础附近区域存在集中分布的危险区域(点安全系数小于1.0 或在1.0 左右),不满足设计安全系数1.35 的要求,桥梁基础附近土体有沿着土-岩界面滑动的风险,故需要对边坡进行加固措施。
拟在桥梁基础前后各设置一排抗滑桩,设置加固宽度为150 m,抗滑桩桩径为2.5 m,间距为5 m,每排共31 根桩,如图2所示。上部抗滑桩的设置是为了抵抗上方的滑坡推力,下部抗滑桩的设置是为了防止下部土体滑动所引起的牵引力,减小桥梁基础区域内土-岩界面单元上的剪应力,从而使得点安全系数有所提高。在桥梁基础前后各设置一排抗滑桩后,土-岩界面的点安全系数分布产生了较大变化,桥梁基础区域点安全系数均大于1.35,满足了设计要求,如图3所示。

图2 抗滑桩加固方案图

图3 抗滑桩加固土-岩界面点安全系数分布图
5 基于点安全系数的加固方案优化
边坡的稳定性受滑面上应力状态的控制,在复杂边坡中,由于上覆土体的厚度、坡度等因素的变化,导致边坡的局部稳定性存在差异。因此,针对边坡不同稳定性的区域,可采取针对性的加固措施,如图4所示。点安全系数法可以很好地评价边坡的局部稳定性,有助于直观地判断边坡需加强支护的区域,优化多余的加固措施,在保证工程安全的前提下,减少支护工程数量,降低工程造价。
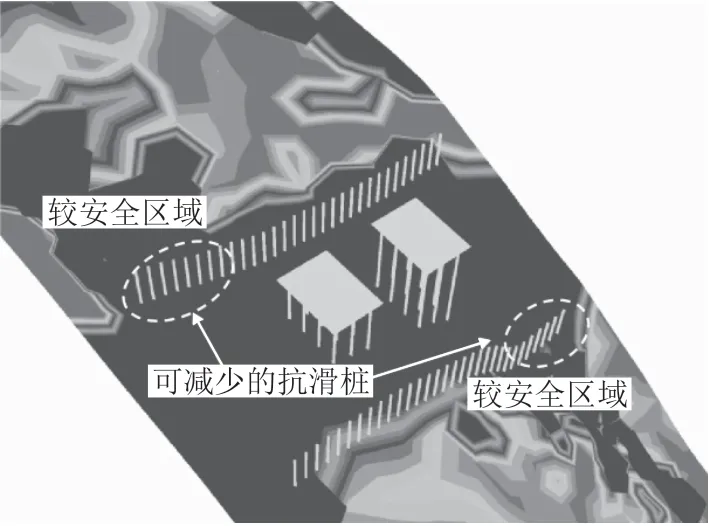
图4 基于点安全系数分布的优化加固方案分析图
由图4 可知,在原加固措施下,虽然桥梁基础范围内的点安全系数均大于1.35,但可见上排抗滑桩左上方和下排抗滑桩右下方的部分区域点安全系数也大于1.35。这表明这些区域的土体抗剪强度还未充分发挥,坡体稳定性较好,边坡能够自稳,故可以减少2 个区域内的抗滑桩数量,节约工程造价。
据此,提出了基于点安全系数的边坡加固优化方案,如图5所示。在减少了相应区域的抗滑桩后,再进行同样的计算得出土-岩界面的点安全系数分布情况,如图6所示。由图6 可知,在减少了部分抗滑桩后,土-岩界面上点安全系数小于1.35 的范围虽有所扩展,但并未影响到桥梁基础的区域。这表明在优化的支护方案下桥梁基础的安全性依然能够得以保障,也说明了基于点安全系数的边坡加固优化方案是可行的。
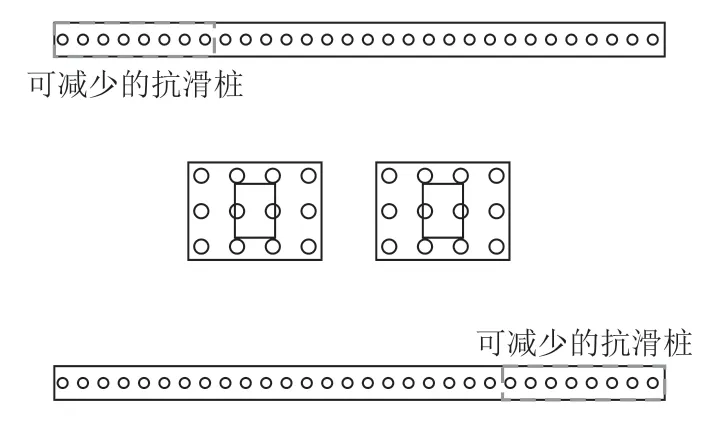
图5 基于点安全系数分布提出的优化加固方案图
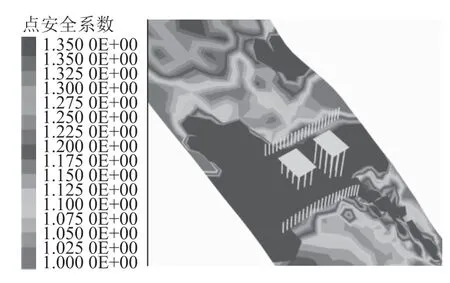
图6 优化加固方案土-岩界面点安全系数分布图
6 结论
本文建立了某桥梁边坡三维有限元计算模型,采用点安全系数法对其土-岩界面上的安全系数分布进行了分析。基于这一分布,提出了抗滑桩加固的优化措施,并通过对比分析,评估了基于点安全系数的二元结构边坡抗滑桩的加固效果,得到主要结论如下:
(1)通过求解边坡土-岩界面的点安全系数分布,可以全面、直观地反映边坡不同位置的安全状况。这一结果对于抗滑桩的加固选位具有较好的指导意义。
(2)根据点安全系数分布提出了抗滑桩的加固优化措施,对比验证了优化前后的点安全系数分布云图,发现只需在边坡点安全系数较小区域进行抗滑桩加固,即可达到规范所要求的加固效果,这最大限度地发挥了边坡体自身的抗剪强度。
(3)本文提出的边坡加固位置选择方法不仅能够提高边坡加固工程的设计施工效率,缩短工期,而且可以避免大量人力财力的浪费,从而降低工程造价。
