基于改进粒子群算法辨识永磁同步电机伺服系统负载转矩及转动惯量*

杨铭 李翔龙 陈兵

1.四川大学机械工程学院；2.创新方法与创新设计四川省重点实验室；3.东方电气股份有限公司

为降低伺服系统的响应时间、提高控制精度，基于神经网络等智能算法设计出的速度环伺服控制器与电机和负载的参数密切相关。对于伺服系统负载转动惯量和负载转矩难以实时测量的问题，本文提出用改进的粒子群算法进行辨识。通过使用非线性变化的学习因子和惯性权重来改善传统粒子群算法易陷入局部最小、收敛速度慢等问题。当电机启动处于加速阶段或运行过程中速度突变超过设定阈值时，采用改进粒子群算法来辨识负载转矩和惯量。论文首先分析永磁同步电机模型，抽象出参数辨识的基本问题，并用改进的粒子群寻优方法解决问题。仿真结果验证了方法的可行性和有效性。

以永磁同步电机(PMSM)为核心运动装置的交流伺服装置被用于高精度控制领域，如数控机床、多轴机械臂等。在实际应用中，复杂的运行工况、电机内部的材料变化等，使电机参数产生变化，例如，机械臂关节的位姿变化，使电机受到的负载转矩和转动惯量在实时变化。而应用于此的高性能控制器设计，大多需要电机和负载的实时参数。

负载端的惯量和转矩识别主要有：（1）离线识别[1]。主要方法有直流衰减法、直接计算法、实验测定法、加减速法等。虽然离线方法能为控制器参数整定提供初始依据，但难以解决电机在运行过程中因参数变化引起的控制性能降低的问题。（2）在线识别[2]。主要方法有滑模观测器法、神经网络拟合方法等智能算法以及递推最小二乘法等常规方法。在线方法虽能在设定的周期内辨识参数，但仍存在需要先验知识、算法复杂度高、收敛慢等问题。

粒子群优化[3](Particle Swarm Optimization，PSO)是受动物觅食行为启发而得到的一种全局随机寻优搜索算法。该算法有众多优点：如控制参数少、无需参数先验知识、计算内存需求少等。但同样存在收敛速度慢、精度低等问题。许多学者提出了不同的改进方式，主要分为对PSO 参数的改进、运动方程的改进和融合其他方法[4]。引用[5]提出了惯性权重随机线性递减的策略，解决了线性递减策略逐渐加强局部搜索而陷入局部最优的缺陷。引用[6]针对PSO 参数固定导致参数辨识精度较差的问题，提出学习因子随惯性权重变化的策略，摆脱局部最优解的陷阱。如图1 所示，引用[7]在引用[8]的基础上提出一个改进均值粒子群算法(MeanPSO)，使用个体极值和全局极值进行速度计算，使算法的搜索范围更大，在算法前期更容易得到最优解，位置更新采用随当前种群适应度大小而改变的方法，增强算法局部勘探能力，加快收敛速度。

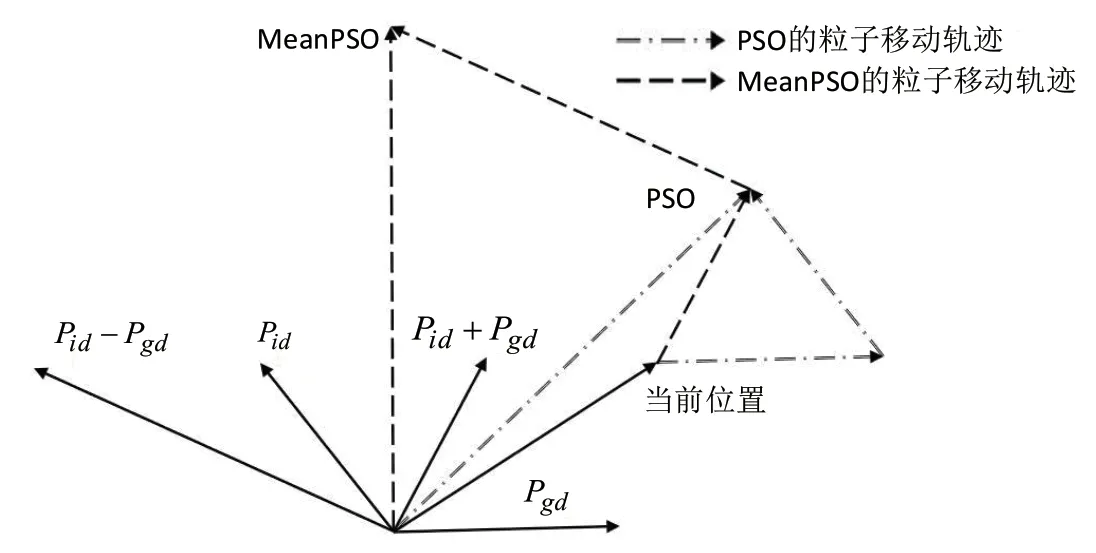
图1 均值粒子群算法原理图Fig.1 Schematic diagram of mean PSO

以上提出的方法虽能提高辨识精度，但也同样增加了算法的复杂性，与粒子群算法本身的原理简单、参数少的优点相悖。所以在不增加算法复杂程度的前提下，本文提出改进学习因子和惯性权重的粒子群算法来实时同步辨识负载转矩及惯量。通过仿真实验对比传统粒子群算法、引用[8]的改进算法和本文提出的改进算法的辨识效果。

1 负载转矩和转动惯量的辨识模型

1.1 永磁同步电机数学模型

在建立PMSM 的模型之前，补充如下条件便于简化分析，可将其视为理想电机[9]：

（1）忽略电机铁芯的饱和；

（2）不计电机中的涡流和磁滞损耗；

（3）电流三相正弦且对称。

这样可得出三相电压方程如式（1）所示：

其中，U、i、ψ分别表示电压、电流和磁链，R为每一相的相电阻。

将式(1)经过Clark 坐标变换和Park 坐标变换后得到dq坐标系下的电压方程如式（2）所示：

定子磁链方程如式（3）所示：

将式(3)代入式(2)中，得到d-q轴电压方程如式（4）所示：

其中，Ud、Uq表示d-q轴电压，id、iq表示d-q轴电流，ψd、ψq表示d-q轴磁链，ωe表示电角速度，Ld、Lq表示的d-q轴电感，ψf表示磁链。

此时电磁转矩方程可写为如式（5）所示：

其中，Te表示电机当前的电磁转矩，pn表示电机的极对数。

另外，电机的机械运动方程如式（6）-式（8）所示：

其中，ωm为电机机械角速度，J为转动惯量，B为阻尼系数，TL为负载转矩，Nr为电机的转速。

1.2 负载转矩和转动惯量的辨识模型

PMSM 模型的运动学方程为式(6)和式(7)，忽略阻尼系数B，式(6)可以简化为如式（9）所示：

伺服系统采样数据因电磁、温度等环境因素的影响存在扰动和噪声误差，要通过多个离散采样点来计算出近似斜率和截距。同样，伺服系统的位置信息由光电编码器采集，当电机处于低转速时，编码器信息会有较大误差。而通过微分得到的加速度数据将放大此误差。综上，式(9)实际上并不是一条直线，只能把采样的离散数据点经过筛选后拟合出一条近似的直线。

记采集的M个离散点为Pi(ω(i),Te(i)),i=1,2,...,M，根据最小方差原理，计算每个离散点到拟合直线距离的平方和，设计适应度函数如式（10）所示：

式（10）中，T是采样周期，表示电机转子和负载的惯量和的估计值， ˆLT表示负载转矩的估计值，C(ω(i),Te(i))为适应度函数。与每个时钟周期相比，假设负载转矩在一个时钟周期内不变化，则负载转矩可以被视为缓慢变化的量。适应度函数是点和拟合线之间距离的平方和的最小值。当取当前迭代的最小值时，可以获得最接近所有离散点的线，这是最佳近似线。

通过工程上的经验可以知道[11]：电机转动惯量的最小值为转子的转动惯量，最大一般为转子惯量十倍。电机空载时为负载转矩的最小值，看作为0，最大一般为额定转矩的三倍。因此，可以获得转动惯量和转矩的经验范围作为优化算法的解空间的搜索域。到目前为止，只需要在解空间中找到惯性矩的估计值和负载转矩的估计值，以最小化适应度函数。

2 改进粒子群算法进行求解

2.1 标准粒子群算法

对于d维的空间，种群中有i个粒子，每个粒子包含两个信息：位置和速度。在搜寻空间中，每一颗粒在各个时间上会对各个个体的方向进行简单的调节，并且将整体粒子的最优轨迹取向，从而寻找整体最优解。该方法采用迭代对各颗粒的速度及位置进行更新，并对多维空间内的运动轨迹进行了动态的调节。再利用适应度函数对各粒子的适应度进行运算，从而得到空间内更好的位置。通过如式(11)和式(12)所示的去更新每个粒子的速度和位置，以便在下一次迭代中进行适应度评估：

式中：i=1,2,…,x；d=1,2,…,D；ϑid(k+ 1)表示在k+1 时刻粒子i在第d维度的速度；pid为个体极值；pgd为全局极值；ω为惯性权重；c1和c2为学习因子；r1和r2是范围为(0,1)的随机数。

2.2 改进粒子群算法

通过式(11)可知，ωidϑ表示上一周期的速度值，它对于粒子的初始移动是非常必要的。接着，c1r1(pid-xid)表示单个个体的信息，是能够让粒子向目前最优的个体极值前进的启发项。第三项c2r2(pgd-xid)表示粒子之间的协同效应，启发粒子向当前全局极值移动。

当ω值过小时，粒子群优化算法全局求优能力较差，局部求优能力较好；当ω值过大时，粒子群优化算法的全局求优能力较强，而局部求优能力较差。因此提出改进的非线性变化惯性权重算法为[12]：提出Y与U两个可变算子，分别在不同情况下，对惯性权重ω进行优化，增强PSO 前期全局搜索能力与后期局部搜索能力，算子及惯性权重的算法如式（13）、式（14）、式（15）所示：

式中：k为当前迭代次数，kmax为最大迭代次数，Y算子与U算子可以通过因子c1和c2进行自适应调整。当c1=0、c2≠0 时，粒子群收敛速度快，容易出现早熟现象；当c1≠0、c2=0 时，粒子只考虑自己的信息，各个粒子之间却交流较少，大大降低收敛的速度，导致粒子会在一定的区间内漂移。

为了获得全局最优值，避免陷入局部最优状态，基于粒子群算法对学习因子c1和c2的值进行动态调整。使用如式（16）和式（17）所示的公式对c1和c2进行自适应优化：

式中：α=β=1。

算法的寻优过程如图2 所示，分为如下几个步骤：

图2 改进PSO 辨识流程图Fig.2 Improved PSO identification flowchart

步骤1：初始化种群粒子数、离散点数、搜索区间和最大迭代次数。在搜索空间对每个粒子赋随机初值。

步骤2：启动电机使之进入加速阶段。采样所需数据后，舍弃电机刚启动时速度100r/min 以下的爬行数据，取连续的离散点作为代入适应度函数的数据集合。

步骤3：把数据集代入适应度函数更新粒子的适应度值。

步骤4：迭代后粒子更新位置、速度、学习因子和惯性权重。比较每个粒子现期与前期的适应度，对个体极值进行记忆与更新。

步骤5：最优的个体极值将被保存为全局极值p_gd，每个个体极值也将被更新保存。

步骤6：当全局极值连续稳定5 次以上或达到最大迭代次数后，结束迭代，全局极值就是得到的解。否则继续迭代更新。

3 仿真结果及分析

为了证明本辨识负载及惯量方法的有效性，在搭建PMSM 仿真模型上进行带载实验。其中辨识转动惯量为0.52e-4，负载转矩为0.05，粒子群的粒子数为20，离散点数据组数为30，最大迭代数为100，传统PSO 和MeanPSO 的惯性因子为0.8，学习因子均为2[3]。本文提出的非线性学习因子和惯性权重变化曲线如图3 和图4所示。辨识结果如图5、图6 所示。

图3 改进PSO 的学习因子曲线Fig.3 Learning factor curve for improved PSO

图4 改进PSO 的惯性权重曲线Fig.4 Inertia weight curve of improved PSO

图5 转动惯量辨识曲线Fig.5 Inertia identification curve

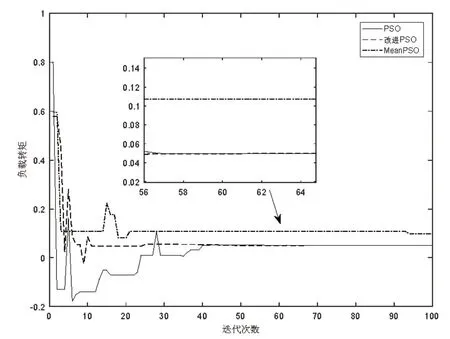
图6 负载转矩辨识曲线Fig.6 Load torque identification curve

通过分析图5 和图6 的辨识结果，经过迭代12 次左右后本文提出的改进粒子群算法收敛，辨识速度较快且精度高，与给定值的相对误差分别为0.07%和4%。而其他两种方法在迭代30 次以上收敛，同时存在精度不足的问题。

4 结论

本文基于针对永磁同步电机负载转矩及惯量的辨识问题，提出基于非线性学习因子和惯性权重的改进粒子群优化辨识算法。此时把伺服系统的负载和惯量辨识问题转化成直线拟合问题，这种问题可以通过算法进行求优。仿真结果显示，这种改进方法在不会增加算法复杂度的同时，可以有效解决粒子群算法本身较慢的收敛速度，容易得到极小值而不是全局最小值等问题。本文虽然验证了算法的有效性，但仍然存在抗干扰能力不足、响应是否及时等问题，在以后的实际使用中需要进一步研究并解决。