基于Relief-WGS 优化算法的图像分类方法*
2023-11-29纪峰马圆月刘莹
纪峰 马圆月 刘莹
1.陕西环保产业研究院有限公司;2.西安微电子技术研究所
针对图像特征选择问题,特征属性过多不但会造成维数灾难,而且会影响分类的正确率。在采用支持向量机分类时,特征维数较高,会造成分类准确率较低,运算速度较慢等问题。为了解决此问题,提出Relief 算法、鲸鱼算法、遗传算法和支持向量机相结合的Relief-WGS 优化算法,实现图像特征选择和分类。首先,使用Relief 算法对特征集进行初步筛选,其次,将筛选的特征子集个数和支持向量机参数编码到鲸鱼-遗传算法中,最后对特征子集进行优化的同时,对支持向量机参数也进行同步优化。计算结果表明,所提出的算法能在去除掉不重要特征的同时对支持向量机参数进行优化,有效地提高图像分类准确率。
近年来,随着图像技术的发展和相关应用的普及,为了能更好地反映图像特征,使图像更有效地应用在多个方面,为此需要在提高图像识别度的问题上不断地进行研究。图像分类准确率的高低取决于所利用的分类特征是否能够很好地反映所要研究的分类问题。一般而言,特征集中或多或少都包含着一些对分类结果无贡献的特征,这些特征也称为冗余特征,过多的冗余特征不仅会使运算变得复杂,处理速度下降,而且可能会导致分类精度降低,因此需要选用对分类识别作用较大的特征[1]。本文对提取的纹理特征进行筛选,根据各个特征和类别的相关性进行特征选择,降低特征空间维数,加快算法的运算效率。
支持向量机(Support Vector Machine, SVM)作为一种基本的监督学习方法,被广泛应用于文本识别、图像识别等[2]。SVM 的原理是通过构建分类超平面作为决策面来最大化不同类型数据之间的差异,有效避免局部最优,在处理有限样本、高维和非线性数据等复杂问题时具有独特的优势。本文结合鲸鱼优化算法和遗传算法来提高算法的精确度和获得全局最优解。遗传算法(Genetic Algorithm,GA)是通过模拟自然进化过程搜索最优化的方法[3]。它有着较好的全局搜索能力和保持种群的多样性,但是计算效率较低。鲸鱼优化算法(Whale Optimization Algorithm)具有强大的全局搜索能力,但是在迭代后期容易陷入局部最优解不能得到全局最优解[4]。因此,将两种算法结合既可以提高算法的精确度又可以达到全局最优解。为了减少前期的运算量,删除不相关的特征属性,减少特征维度,利用Relief 算法进行特征选择。Relief 算法是一种针对二分类问题通过计算特征权重对特征进行选择的方法。根据各个特征和类别的相关性赋予特征不同的权重,权重小于某个阈值的特征将被移除[5]。采用这种方法可以在分类前期降低样本维数,减少计算量。
综上所述,本文提出了一种Relief-WGS 优化算法。该算法首先使用Relief 算法对特征集进行初步筛选,其次,将筛选的特征子集个数和SVM 参数一起编码到鲸鱼-遗传算法中,再对特征子集进行优化的同时,对SVM 参数进行同步优化,实现图像分类。
1 原理与方法
首先利用Relief 作为特征预选器滤除相关性小的特征,以WSO-GA 作为搜索算法,SVM 的分类精度作为评估函数,在剩余特征中选择最优特征子集,最后利用SVM 分类器对所选择的最优特征进行分类。
1.1 Relief 算法
Relief 算法是一种典型的过滤式算法,在对特征样本进行选择与分类的过程中相互独立,过滤式算法的通用性比较强并且计算的复杂度比较低,适合对大数据的特征样本进行特征选择[6]。Relief 算法中特征和类别的相关性是基于特征对近距离样本的区分能力。核心原理是根据各个特征和类别之间的相关性给每个特征不同的权重,将权重和阈值进行比较,当权重比阈值小时则将该特征删除。权重值越大则表明该特征代表某图像的能力越强,反之权重越小则该特征代表某图像的能力越弱。
1.2 支持向量机
SVM 算法是一个凸优化问题,其原理是用分离超平面作为分离训练数据的线性函数,解决线性分类问题。假设训练样本集合其中,xi∈Rn表示训练样本,yi∈ {1 , - 1}表示输入样本的类别。训练的最终目的是找到一个最优分类面,使得两类样本之间以最大间隔分开,使泛化误差达到最小或者有上界。这个最优分类面即超平面,该超平面可描述为如式(1)所示:
式(1)中x为样本,ω为权向量,b为分类阈值。
1.3 鲸鱼-遗传算法
遗传算法(Genetic Algorithm, GA)是一种依据生物界优胜劣汰的进化准则衍生出的随机优化搜索方法。GA 算法的核心思想是先随机得到一个父代种群,通过计算种群中每一个个体的适应度值,然后对得到的值进行排序,从中找出适应度值最大或最小的n个个体,确定种群的进化方向,然后对个体中的染色体进行遗传操作,得到新的子代种群,经过有限次迭代之后,得到问题的近似最优解,GA 算法包括三个基本操作:选择、交叉和变异。
鲸鱼优化算法是一种基于复杂优化问题进行寻优的算法,模拟了座头鲸群体的捕猎行为。该算法可分为包围收缩、螺旋捕食和搜索猎物三步。
(1)包围收缩。该阶段对鲸群识别猎物并且收缩包围圈的动作进行模拟。
(2)螺旋捕食。在围捕猎物时,鲸鱼通过螺旋向上游动的方式向猎物移动并吐出气泡对猎物进行捕食,即在螺旋更新位置的同时对包围圈进行收缩。
(3)搜索猎物。当≥1时,鲸鱼随机选择一个领导个体,以此进行全局搜索。
对于参数优化问题,GA 算法有着较好的全局搜索能力和种群的多样性,但由于要经历选择、交叉和变异三步操作才能得到下代种群,因而计算效率较低,收敛速度较慢。由于鲸鱼算法在控制参数寻优时会出现实际的优化搜索过程不能完全体现,导致存在求解精度低、收敛速度慢和易陷入局部最优的缺点。因此,将遗传算法与鲸鱼算法进行结合可以提升算法的收敛效果[7]。
2 Relief-WGS 优化算法
基于以上研究,提出Relief-WGS 优化算法,其流程图如图1 所示。该算法首先使用Relief 算法对数据特征集进行初步的筛选,然后将SVM 的参数和筛选的特征子集编码到WOA-GA 算法中,以SVM 的分类精度构建适应度函数,同时优化特征子集和SVM 的参数,具体流程分为如下几个步骤:

图1 Relief-WGS 算法流程图Fig.1 Relief-WGS algorithm flowchart
步骤1:采用Relief 算法对图像特征进行第一次提取,得到特征矩阵;
步骤2:WOA-GA 算法进行参数初始化,种群大小为30,迭代次数为50,算法的终止条件为达到迭代次数或连续十代的适应度值不变;
步骤3:生成初代种群,由于SVM 的惩罚系数C和核参数σ采用实数编码,而对特征的二次筛选是通过0、1 进行,0 表示没有选择该特征,1 表示选择该特征,采用二进制编码;
步骤4:将个体的后N位带入样本中进行特征的第二次筛选;
步骤5:将个体的前两位带入SVM 模型中,结合二次筛选的训练样本,确定SVM 分类模型;
步骤6:将二次筛选测试样本带入确定的SVM 中,得到分类结果;
步骤7:计算初代种群的适应度值;
步骤8:根据初代种群的适应度值进入鲸鱼算法中,计算每一头鲸鱼的适应度值,更新个体位置;
步骤9:将位置更新的鲸鱼个体代入到遗传算法中,经过交叉和变异操作,得到新的种群;
步骤10:返回步骤4,计算新种群的适应度值;
步骤11:判断是否满足终止条件,若满足,则输出最终结果;若不满足,继续对种群进行处理,直至满足终止条件,得到最终结果。
3 实验结果
本实验为了验证Relief-WGS 算法的有效性,将特征子集个数和SVM 参数一起编码到WOA-GA 算法中,在对SVM 参数进行优化的同时对所有特征进行同步优化。在实验时需要对数据和参数进行如下几步处理。
3.1 数据的预处理
为了提高SVM 的分类准确率,将需要用于分类的所选数据样本进行归一化处理,并将其分为训练样本和测试样本进行后续分类。
3.2 参数选择方法
本文使用WOA-GA 算法对SVM 的参数进行优化。设置算法的迭代次数为50,个体长度设定为2,遗传算法中交叉和变异概率是基于适应度值自适应计算得来的,鲸鱼算法位置更新是根据适应度值计算。
适应度函数统一设置为如式(2)-式(4)所示:
式(2)中we1为训练样本识别结果的权重,we2为测试样本识别结果的权重,m1为训练样本的总数,m2为测试样本的总数,nsv1为训练样本分类正确的结果,nsv2为测试样本分类正确的结果,fitness越小,表明综合的分类准确率越高[8]。
3.3 模型建立
利用从每组训练样本中选择优化后的核参数来对样本进行新一轮的训练,获得SVM 的分类模型,然后通过测试样本来测试模型的分类精度。实验选取UCI 数据库中的5 种数据集进行试验,所选取数据集的基本信息如表1 所示。

表1 实验数据集Tab.1 Experimental datasets
利用Relief 算法对提取的特征进行筛选,保留与目标类别相关性较大的特征,然后利用WOA-GA 算法优化参数的SVM 算法对特征子集和核参数进行同步优化,获得优化后的特征子集。优化特征子集的个数如表2 所示。
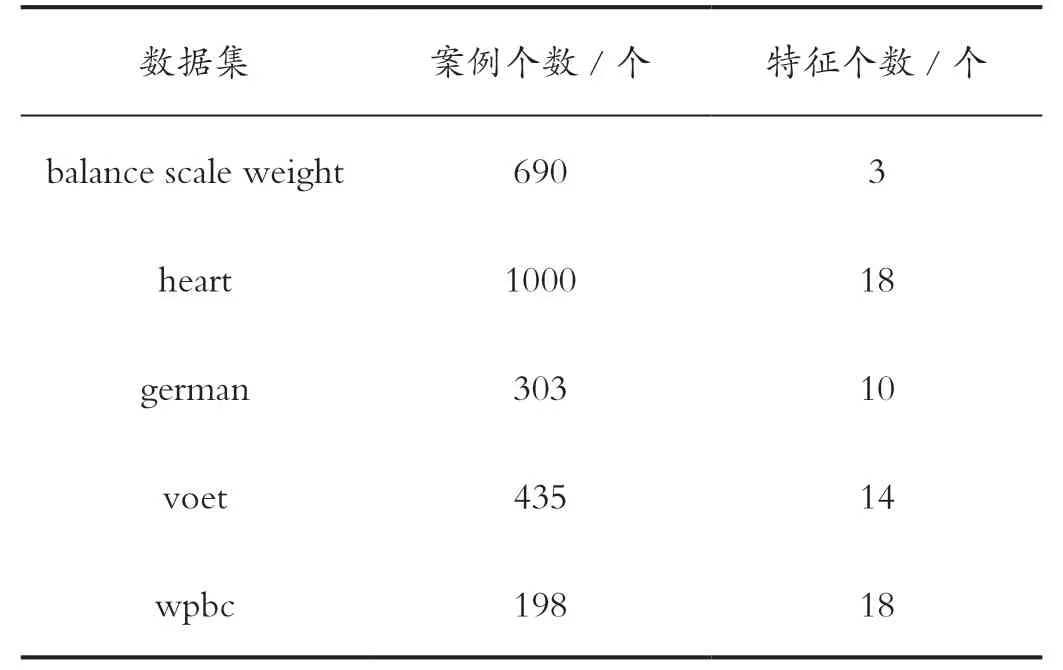
表2 优化特征子集个数Tab.2 Number of optimized feature subsets
获取的优化特征子集通过表2 可知,利用选择的多个优化特征,以SVM 为分类器进行分类,其中SVM 选用RBF 为核函数。为进一步验证Relief-WGS 优化算法的有效性,分别和默认核参数的SVM、采用WSO-GA算法优化参数的SVM(WGS)、Relief 算法优化特征的SVM(Relief-SVM)进行分类结果的比较。通过比较分类准确率来评价特征选择方法的优劣,如表3 所示。
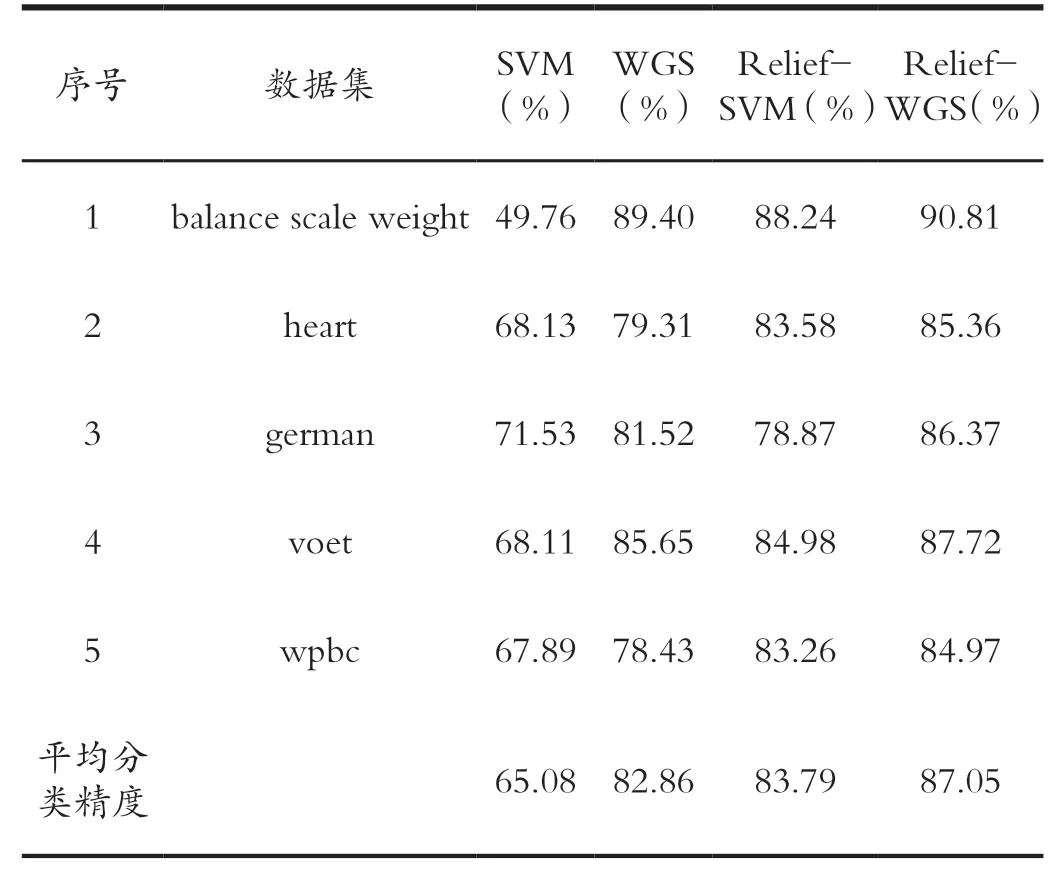
表3 数据集分类结果对比Tab.3 Comparison of dataset classification results
通过表3 可知,本文提出的Relief-WGS 优化算法可以同时优化特征子集和SVM 的参数,实现以优化的特征子集和优化的SVM 参数来提高分类的准确率。为了进一步验证Relief-WGS 优化算法的有效性,将其与SVM、WGS 和Relief-SVM 进行比较,实验结果显示:
(1)对于任意的特征数据而言,使用WGS 优化算法进行参数寻优后的分类准确率比采用默认参数的SVM高,证明了对传统的SVM 中的参数进行寻优,找到优化的控制参数,可以提高SVM 的分类准确率。
(2)使用Relief-SVM 优化算法对输入的特征向量筛选后进行分类,分类准确率均有提高,证明了利用Relief-SVM 对输入的特征数据集进行筛选和优化,得到优化的特征子集,去除掉一些特征不明显的影响因素,减少不重要因素对分类造成的影响,可以提高分类的准确率。
(3)使用本文提出的Relief-WGS 优化算法得到的分类准确率最高,证明在对特征子集和SVM 的参数同步进行优化时,去除掉不重要的特征并对参数进行优化可以得到更好的分类效果。
4 结论
本文提出一种Relief-WGS 优化算法,同时优化特征子集和SVM 的参数,实现用优化的特征子集和优化的SVM 参数来提高分类的准确率。通过与传统的SVM、WGS 算法和Relief-SVM 算法相比,本文所提算法将图像的平均分类准确率分别提高了21.97%、4.19%和3.26%,证明了图像分类识别的准确性。结果表明,本文提出的特征选择方法利用最少的特征获得了最高的分类精度,更有效地用于特征选择分类。
