中国城市全要素生产率变化测度与收敛性检验研究

夏永红

（江苏师范大学 商学院，江苏 徐州 221116）

一、引言及文献综述

2015 年3 月中国政府首次在政府工作报告中提出“增加研发投入，提高全要素生产率”。2017 年10 月，党的十九大报告中明确提出“推动经济发展质量变革、效率变革、动力变革，提高全要素生产率”。2022 年10 月，党的二十大报告中进一步明确提出，为了实现中国式现代化发展，推动经济实现高质量发展，并提出三个“着力”，即“着力提高全要素生产率，着力提升产业链供应链韧性和安全水平，着力推进城乡融合和区域协调发展”。自2017 年以来，我国经济已由高速增长转向高质量发展阶段，经济增长方式也由要素投入型增长转向由科技进步、组织创新和生产创新带来的全要素生产率增长。推动我国经济高质量发展，就必须将经济增长方式由要素驱动型为主向创新驱动型为主转变，就必须提高全要素生产率。探寻提高全要素生产率的对策建议，以期为促进国家及城市高质量发展具有重要的现实意义。

目前，关于全要素生产率(TFP)的研究主要从研究对象和研究方法两个层面展开分析。从研究对象来看，现有文献主要从企业、部门、区域或国家视角进行分析；从研究方法来看，主要有生产函数、增长核算、随机前沿分析(SFA)，以及数据包络分析(DEA)等方法[1，2]。其中，DEA 方法是利用非参数估计生产前沿面的技术进步效率，该方法无需对函数形式和数据分布进行假设，同时具有计算简单和对全要素生产率变化进行分解的优点，因此，基于DEA 分析的各种Malmquist 生产率指数得到广泛的应用。Malmquist 指数由瑞典经济学家Sten Malmquist 于1953 年提出，Caves 等(1982)将其引入到了生产领域，使用距离函数之比来度量生产率的变化[3]。随后，Fare 等(1994)基于DEA方法测算Malmquist 生产率指数，并将其分解为技术变化、纯效率变化和规模变化[4]。Paster&Lovell(2005)提出了Global Malmquist 生产率指数，基于Global 技术求得的结果具有乘法完备性、允许技术退化，同时避免了线性规划无可行解的问题，Global Malmquist 生产率指数可以分解为效率变化和最佳实践差距变化(the Change in Best Practice Gap，BPC)，最佳实践差距变化(BPC)可以大于、等于或小于1，分别表示t+1 期的基准技术相较于t期的基准技术接近还是远离了全域的基准技术[5]。Oh&Lee(2010)为了解决基于技术异质性的效率评价问题，基于共同前沿面(Metafrontier)提出了Meta-Malmquist 生产率指数，Meta-Malmquist 生产率指数在Global Malmquist 生产率指数的基础上，Meta-Malmquist 生产率指数可以比较不同组群的生产率变化，进一步将其分解为同期基准技术的效率变化(EC)、同期基准技术和跨期基准技术之间的最佳实践差距变化(BPC)，以及跨期基准技术与全域基准技术之间的技术领先变化(TGC)[6]。

关于经济增长的收敛性分析主要集中在收入方面，对全要素生产率的收敛分析相对较少。Miller &Upadhyay(2002)利用Cobb-Douglas 生产函数的索罗余值测算OECD 国家全要素生产率并对其进行收敛性检验[7]。彭国华(2005)利用该方法进行了类似的研究，认为中国全国范围内的全要素生产率不存在绝对收敛，只有条件收敛，同时，三大地区中只有东部地区存在俱乐部收敛现象[8]。李静等(2016)采用超越对数形式的SFA 模型对中国2002—2012 年285 个城市的全要素生产率变化进行测算，并对其进行了收敛性检验[9]。何彬、范硕(2013)对中国31 个省份国有经济基于Meta-Malmquist 生产率指数进行了随机收敛性检验[10]。李健和盘宇章(2018)、保永久和丁君涛(2021)采用基于DEA 模型的Malmquist 指数分别对中国城市全要素生产率进行了测度和收敛性检验分析[11，12]。

综上所述，文章在现有文献研究的基础上，考虑到我国东部、中部和西部地区存在的技术异质性，利用Meta-Malmquist生产率指数对中国2005—2020 年284 个城市全要素生产率变化进行测度并对其进行分解，以便考察不同地区的追赶效应、创新效应和技术领先效应，同时，通过σ 收敛和β 收敛检验中国及各地区的全要素生产率变化是否存在收敛性。

二、全要素生产率变化的测度

1. 基本方法

Oh&Lee(2010)提出的Meta-Malmquist 生产率指数主要通过分别定义组群前沿和共同前沿，以便更好地刻画不同地区生产率变化的异质性[6]。假设有K个决策单元进行了T期生产，全部决策单元可分为j个组群，依次为R1，R2，…，Rj，每个组群具有不同的生产技术集，每个决策单元i均使用N种投入，得到M种产出，，则生产技术集被定义为：P={(x，y)计算Meta-Malmquist 生产率指数需要定义三个基准技术集，即当期的基准技术、跨期的基准技术和全域的基准技术集。

Rj组的当期的基准技术定义为（表示规模报酬不变），t=1，…，T，λ>0。Rj组中决策单元i的当期Malmquist 生产率指数定义为，具体公式如下：

公式(1)表示产出方向的距离函数为：Ds(x，y)=inf{φ>0被定义为当期的生产技术集。

Rj组的跨期基准技术由Rj组的整个观测值和整个时间段的观测值构成的一个生产可能集，有j种不同的跨期基准技术，一种跨期基准技术中的生产者不能轻易进入另一种跨期的生产技术集进行生产。Rj组的跨期基准技术定义为的基础上，Rj组的跨期Malmquist 生产率指数定义如下：

公式(2)表示产出方向的距离函数为：DI(x，y)=inf

全域基准技术由所有组、所有时期的全部观测单元构成的一个生产可能集。所有组全域的基准技术集定义为：PG=conv在PG生产技术集的基础上，Meta-Malmquist 生产率指数定义为：

公式(3)表示产出方向的距离函数为：DG(x，y)=inf{φ>0

Meta-Malmquist 生产率指数可以分解为组内效率变化、组内技术变化和技术领先变化三个部分，即反映了追赶效应、创新效应和技术领导效应，表示如下：

公式(4)中，TGs、BPGI，s(s=t、t+1)分别表示观测单元的技术效率和最佳实践差距；EC表示效率的变化；BPC表示在之间的最佳实践差距的变化，主要测量组内技术的变化，当BPC>1 时，表明t+1 期的当期基准技术相较于t期更接近于跨期基准技术，表示技术进步；当BPC<1 时，表明t+1 期的当期基准技术相较于t期远离了跨期基准技术，表示技术退步。TGRs(s=t、t+1)表示Rj组观测单元的技术差距比例，Rj组技术水平与全域技术集定义的潜在技术水平之间的技术差距。TGR越小，Rj组的技术水平越远离全域前沿技术。TGR=1 的观测单元表示位于全域前沿面上，是新技术创新的领导者。TGC测量技术领导地位的变化。

为了计算和分解城市k′在时期t和t+1 之间的Meta-Malmquist 生产率指数变化，需要解决以下六个不同方向距离函数的线性规划问题：Ds(xs，ys)，DI[xs，ys/Ds(xs，ys)]和DG[xs，ys/DI(xs，ys)]，s=t，t+1。产出方向距离函数是Farrell 基于产出技术效率倒数的关系计算当期、跨期和全域六个方向距离函数。

当期产出距离函数的线性规划求解如下：

公式(5)中，λk，s是一个强度变量，表示参考标杆的权重系数。

跨期产出距离函数的线性规划求解如下：

全域产出距离函数的线性规划求解如下：

根据方程(5)~(7)的最优解可以计算Meta-Malmquist 的生产率指数。

2. 数据来源

文章选取2005—2020 年中国大陆284 个地级及以上城市作为研究对象。根据2021 年《中国城市统计年鉴》中城市区划主要有地级市及以上城市297 个，在2005—2020 年间，由于城市的调整和部分数据缺失等原因，将安徽巢湖（2011 年调整为县级市）、山东莱芜（2019 年调整为济南市莱芜区）、海南三沙和儋州、贵州毕节和铜仁、青海海东、新疆吐鲁番和哈密，以及西藏自治区的6 个地级市样本去掉。其相关数据来源于历年《中国城市统计年鉴》《中国统计年鉴》和EPS 数据库。

3. 变量选取

基于DEA 方法的Meta-Malmquist 生产率指数的计算，需要从投入要素和产出要素两个层面选取评价指标，其中，投入要素包括劳动和资本投入，产出要素可以用总产值、增加值或利润指标来衡量。

（1） 劳动投入变量

劳动投入主要采用城市劳动就业人数进行衡量，劳动就业人数包括城镇单位从业人员和城镇私营与个体从业人员。

（2） 资本投入变量

资本投入通常可以采用城市资本存量和城市固定资产投资水平进行衡量，文章选取资本存量水平进行估算。估算资本存量一般采用Goldsmith 于1951 年提出的永续盘存法[13-15]，资本存量的估算公式为：

公式(8)中，i表示城市，t表示年份；Kit表示第t年的资本存量，Kit-1表示第t-1 年的资本存量，在此表示基期的资本存量。借鉴张军等(2004)[14]的方法，利用2005 年城市固定资产投资额除以10%作为城市的初始资本存量；δ 表示经济折旧率，张军等(2004)和单豪杰(2008)计算固定资本形成总额的经济折旧率分别为9.6%和10.96%[14，15]，文章选取10.96%作为城市固定资本形成总额的经济折旧率；Iit表示i城市第t年固定资产投资总额，固定资产投资额利用固定资产投资价格指数，以2005年为基期进行指数平减。

（3） 产出变量

产出指标主要以中国284 个地级及以上城市的地区生产总值(GDP)进行衡量，同时利用地区生产总值指数以2005 年为基期进行平减处理，以消除价格因素的影响。具体变量的描述性统计如表1 所示。

表1 变量的描述性统计

三、城市全要素生产率变化结果分析

1. 全国城市全要素生产率变化的结果分析

基于Meta-Malmquist 生产率指数的求解方法，借助Stata17软件计算2005—2020 年中国284 个城市全要素生产率指数，并将其分解为组内效率变化(EC)、最佳实践差距变化(BPC)和技术领先变化(TGC)，其中，2005—2020 年中国284 个城市的全要素生产率变化的演变趋势如图1 所示。

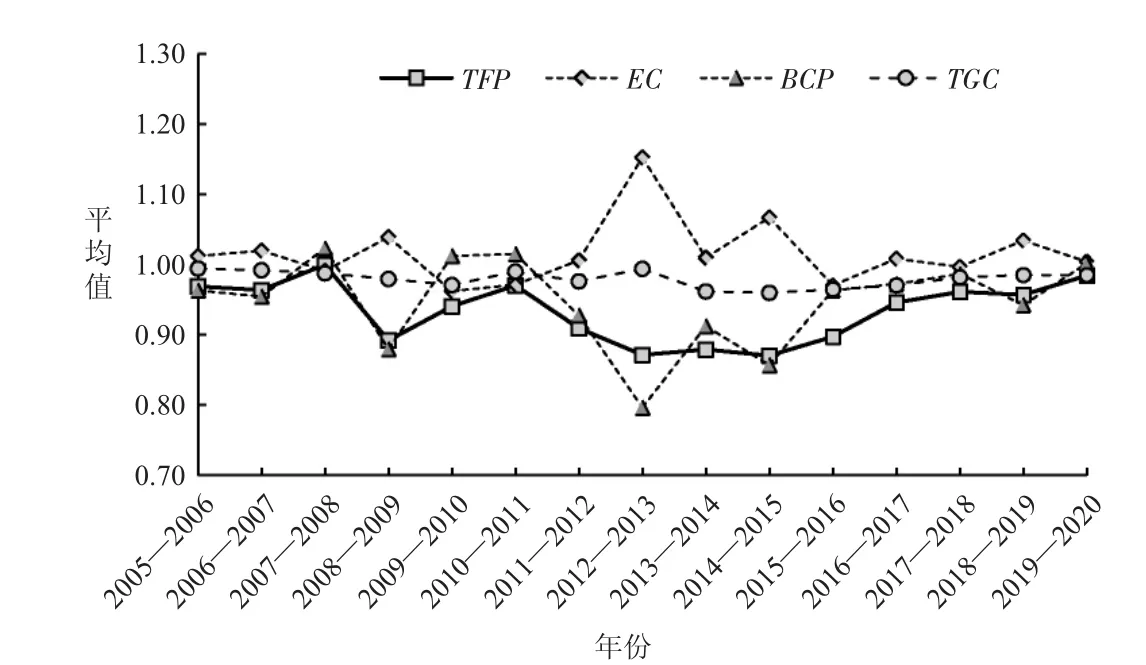
图1 全国城市全要素生产率变化及其分解指数的演变趋势

由图1 可以看出，在2005—2020 年间，中国城市全要素生产率(TFP)由0.9688 上升到0.9841，期间上升了0.0153。其中，2015 年城市全要素生产率降到了最低点(0.8703)，在2005—2015 年间呈现波动下降趋势，而在2016—2020 年间，即整个“十三五”期间呈现不断上升的趋势。从中国城市全要素生产率的分解指数中可以看出，同期基准技术的组内效率变化(EC)略有下降，从2006 年的1.0121 下降到2020 年1.0038，2013 年出现较大幅度的波动，研究期间组内效率均值大于1，说明284 个城市的组内效率不断提升；同期与跨期之间的最佳实践差距(BPC)提高了0.0380，2013 年出现较大幅度的下降，达到期间最低点(0.7963)，2020 年最佳实践差距变化大于1，代表生产技术的进步；技术领先变化(TGC)相对较为稳定，在2005—2020 年间下降了0.0088。总体而言，在2005—2020 年间，中国城市全要素生产率变化增长了0.0154，最佳实践差距(BPC)提高了0.0380，而组内效率变化(EC)和技术领先变化(TGC)分别下降0.0084 和0.0088。

2. 区域城市全要素生产率变化的结果分析

Meta-Malmquist 生产率指数解决了不同组间的可比性问题，因此，更能有效地对不同区域的全要素生产率及其分解指数进行对比分析，全国及东部、中部和西部地区城市全要素生产率变化及其分解指数的均值如表2 所示。

表2 2005—2020 年区域城市全要素生产率变化及分解指数的平均值

由表2 可以看出，在2005—2020 年间全国和三大区域城市全要素生产率变化主要来自于组内效率变化(EC)，组内效率变化均值大于最佳实践差距变化(BPC)和技术领先差距变化(TGC)。在此期间，284 个城市全要素生产率的组内效率变化提高了1.62%，其中，东部地区城市全要素生产率的组内效率变化(EC)最大，年均提高3.19%；中部地区提高了1.41%，西部地区接近1。284 个城市同期基准技术和跨期基准技术之间的最佳实践差距变化(BPC)平均下降了5.30%，东部、中部和西部地区分别下降了7.70%、2.58%和5.68%，其中，西部地区最佳实践差距变化均值最大。284 个城市跨期基准技术与全域基准技术之间的技术领先变化(TGC)平均下降了2.06%，通过比较东部、中部和西部地区的跨期基准技术与全域基准技术之间的技术领先差距变化(TGC)，能更好地分析东部、中部和西部地区的技术领先地位的变化，其中，西部地区基准技术与全域基准技术的技术领先差距下降了0.67%，而中部地区与全域基准技术的技术领先差距下降了5.30%，东部地区则一直处于技术领先地位，具有技术领先效应。

四、中国城市全要素生产率变化的收敛性检验分析

检验经济增长收敛性的方法主要有σ 收敛和β 收敛，其中，β 收敛又可以分为绝对β 收敛和条件β 收敛[16-18]。σ 收敛体现经济发展水平随着时间的推移而趋于一致，经济发展水平的差距不断缩小；而β 收敛则表现为落后地区相对于富裕地区有更快的经济增长速度或较高的全要素生产率增长，但经济发展水平不一定趋于一致，因此，σ 收敛与β 收敛具有如下关系：β收敛是σ 收敛的必要非充分条件，σ 收敛则是β 收敛的充分非必要条件，即如果存在σ 收敛则必然存在β 收敛，如果不存在σ 收敛，通常需要进一步检验是否存在β 收敛。

1. σ 收敛检验

σ 收敛意味着城市全要素生产率变化的离散程度随着时间的推移不断降低，否则不存在σ 收敛，σ 收敛可以采用标准差、方差和变异系数进行衡量，文章主要采用城市全要素生产率变化对数的标准差进行σ 收敛性检验，检验公式如下：

公式(9)中，Std(lnTFP)t是t时期城市全要素生产率变化对数的标准差。φ2为σ 收敛系数，如果φ2为负值且显著，则说明存在收敛；如果φ2为正值且显著，则说明存在发散；如果φ2值不显著，则说明不存在σ 收敛或发散。φ1和εt分别代表常数项和随机误差项。中国284 个城市及三大区域2005—2020 年全要素生产率变化的σ 收敛检验和全要素生产率变化对数的标准差如表3 和图2 所示。

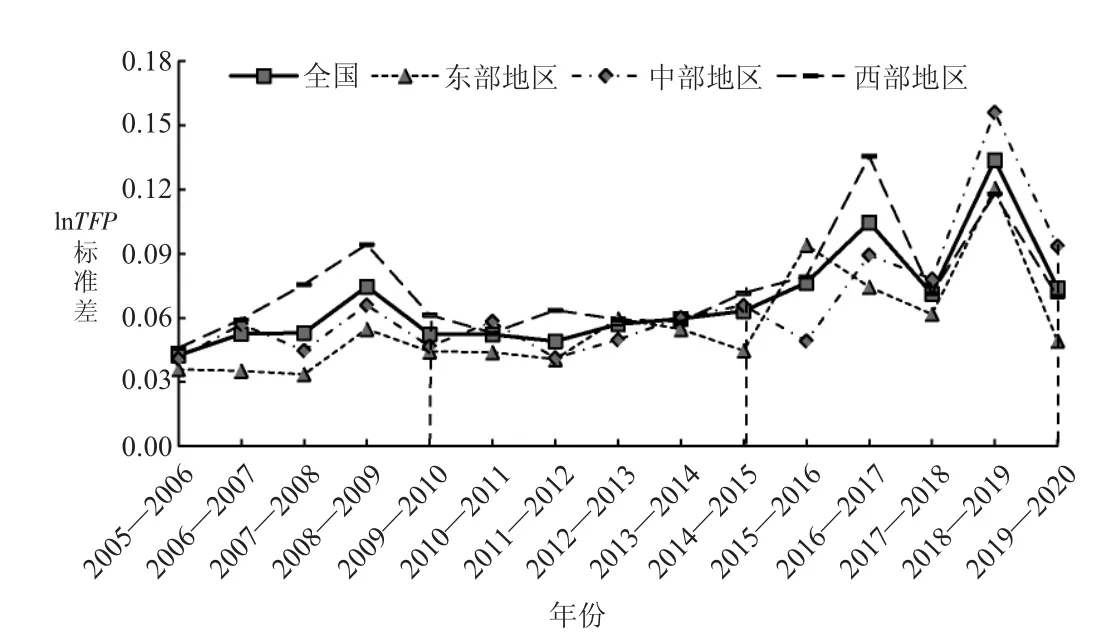
图2 全国和三大区域城市全要素生产率变化对数的标准差

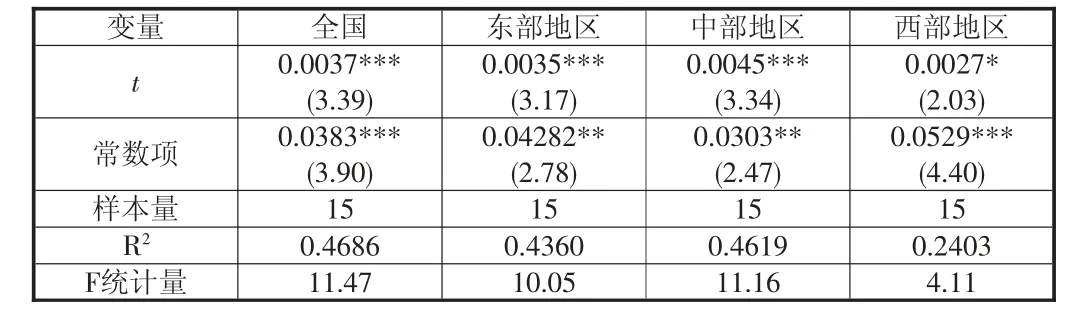
表3 全国和三大区域城市全要素生产率变化的σ 收敛检验结果

从表3 可以看出，在2005—2020 年间，全国和三大区域城市全要素生产率变化不存在σ 收敛，其回归系数φ2均为正值且在1%或10%的显著性水平下显著，说明全国和三大区域城市全要素生产率变化的离散程度随着时间的推移不断提高，存在发散趋势。结合表3 和图2 可以看出“三个五年计划”期间全国和三大区域城市全要素生产率年平均变化的离散程度不同，其中，在“十一五”期间，全国和三大区域城市全要素生产率变化的标准差呈现先上升后下降的趋势；在“十二五”期间相对较为稳定，全国和三大区域城市全要素生产率变化没有呈现明显的收敛和发散特征；而在“十三五”期间全国和三大区域城市全要素生产率变化呈现出“发散、收敛、再发散、再收敛”的“M”型演变特征。总之，在2005—2020 年间全国和三大区域的城市全要素生产率变化不存在σ 收敛，因此，需要进一步检验中国城市全要素生产率变化的σ 收敛。

2. β 收敛检验

（1） 绝对β 收敛

绝对β 收敛是指一定时期内某个国家、地区或城市的某一经济增长变量是否趋于相同的稳定状态，如果城市全要素生产率变化的增长率与初始城市全要素生产率变化呈现负相关，即全要素生产率变化较低的城市比全要素生产率变化较高的城市有更快的增长速度，说明不同城市全要素生产率变化存在绝对β 收敛。在Sala-I-Martin(1996)[18]、Miller&Upadhyay(2002)[7]研究的基础上，通过以下模型检验城市全要素生产率变化的绝对β收敛性。

其中，i表示第i个城市；t0表示初始年份；T表示研究期间的时间跨度；TFPi，t0和TFPi，t0+T分别表示基期和末期的全要素生产率变化；α 为常数项，β 为收敛系数，如果β 值小于0，则说明不同城市全要素生产率变化存在绝对β 收敛；μit表示随机误差项。通过模型(10)对全国及三大区域进行估计，其估计结果如表4 所示。

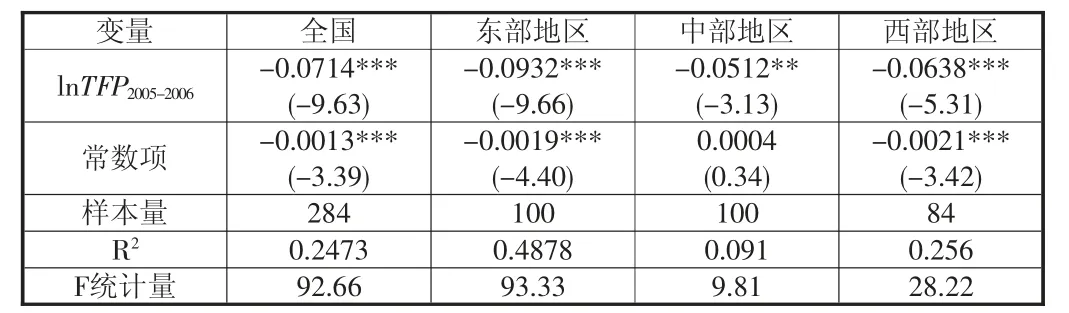
表4 全国和三大区域城市全要素生产率变化的绝对β 收敛检验结果

从表4 可以看出，在2005—2020 年间，全国和三大区域的回归结果显示其收敛系数β 均小于0，且在1%或5%的显著性水平下显著，即在全国和三大区域范围内，全要素生产率增长较低的城市比全要素生产率增长较高的城市具有更快的增长速度，存在绝对β 收敛。从三大区域收敛系数β 值的大小可以看出，东部地区全要素生产率变化的收敛速度最大，其次是西部和中部地区。

（2） 条件β 收敛

条件β 收敛表明每个城市全要素生产率变化都拥有自己的稳定状态，每个城市全要素生产率率变化的稳定状态取决于城市的经济状况。具体估计模型如下：

其中，i表示第i个城市；TFPi，t和TFPi，t-1分别表示第 期和滞后一期的全要素生产率变化；αc为常数项，βc为条件收敛的估计系数；X表示一系列控制变量，ψ 表示相应的估计系数，文章选取城市产业结构(instr)和科技创新发展(sciedu)两个控制变量。其中，城市产业结构指标借鉴徐敏和姜勇(2015)[19]的方法，同时考虑第一、第二和第三产业，具体计算公式为：instr=∑qi×i=q1×1+q2×2+q3×3，其中qi为城市第i产业增加值的比重；科技创新发展水平指标主要采用城市科技和教育支出占财政一般预算内支出的比重进行衡量，城市科技教育经费支出比重越大越有利于吸引高水平科技人才，有利于城市科技创新水平的提升。通过模型(11)对全国及三大区域进行估计，其估计结果如表5 所示。

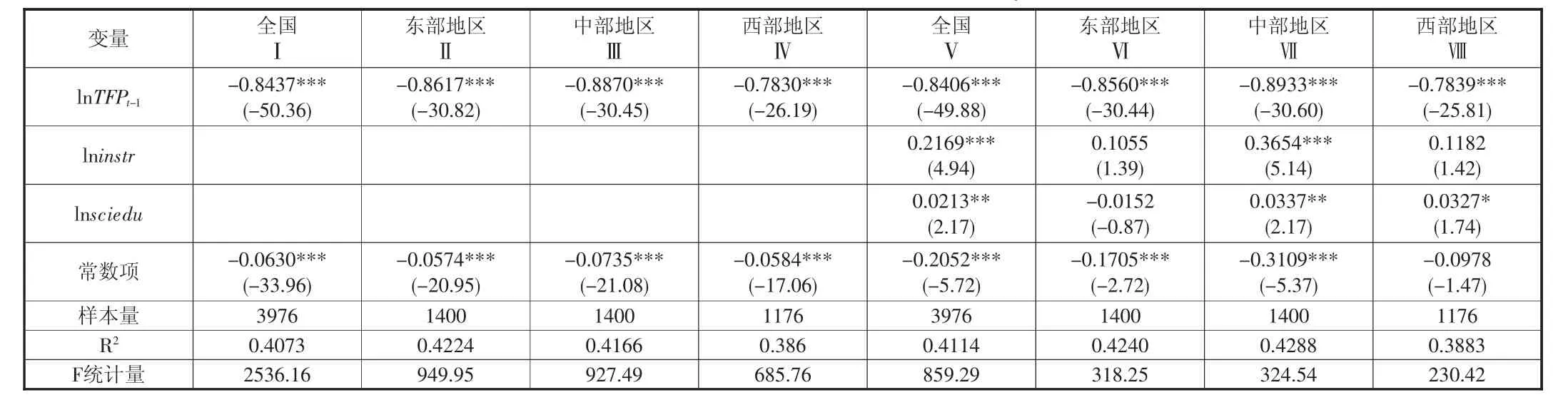
表5 全国和三大区域城市全要素生产率变化的条件β 收敛检验

从表5 可以看出，列Ⅰ~列Ⅵ显示了不考虑控制变量中国284 个城市与东部、中部和西部地区城市全要素生产率变化的条件β 收敛估计结果，即β 收敛系数均小于0，且在1%的显著性水平下显著，说明中国和三大区域城市全要素生产率变化存在条件β 收敛，其中，中部和东部地区条件β 收敛系数的绝对值大于全国平均值，西部地区城市全要素生产率变化的条件收敛系数低于全国平均值。考虑到估计结果是否具有稳健性，分别加入城市产业结构和科技教育发展水平两个控制变量，列Ⅴ~列Ⅷ显示了全国及三大区域条件β 收敛的回归结果。从考虑控制变量的回归结果可以看出，全国和三大区域城市全要素生产率变化的β 估计系数仍然均小于0，且在1%的显著性水平下显著，说明每个城市全要素生产率的变化都拥有自己的稳定状态，受到城市产业结构和科技创新发展水平的影响。从全国和中部地区的回归结果可以看出，城市产业结构和科技创新水平对城市全要素生产率变化增长率具有正向影响作用；而城市产业结构发展在东部和西部地区影响不显著，科技创新发展水平在西部地区影响不显著。总之，增加城市产业结构和科技创新发展水平两个控制变量后，并没有影响城市全要素生产率变化的条件β 收敛检验，即284 个城市和三大区域城市全要素生产率变化存在条件β 收敛。

五、研究结论与启示

文章主要对中国城市全要素生产率进行测度并对其收敛性进行分析，得到如下几点结论：

第一，利用Meta-Malmquist 生产率指数测算了中国284 个城市和三大区域城市的全要素生产率变化，并对其进行分解为组内效率变化、最佳实践差距变化和技术领先变化。在2005—2020 年间，284 个城市全要素生产率变化呈现先下降后上升的趋势，总体变化增长了0.0154，其分解指数最佳实践差距变化提高了0.0380，而组内效率变化和技术领先变化分别下降0.0084 和0.0088。在2005—2020 年间全国和三大区域城市全要素生产率变化主要来自于组内效率变化，组内效率变化均值大于最佳实践差距变化和技术领先差距变化，其中，东部地区组内效率变化均值最大；东部地区技术领先差距变化均值等于1，说明东部地区具有技术领先效应。

第二，利用β 收敛、绝对β 收敛和条件β 收敛三种方法对中国284 个城市和三大区域城市的全要素生产率进行收敛性检验。检验结果显示，在样本期间内全国和三大区域城市全要素生产率变化不存在σ 收敛，但是存在绝对β 收敛和条件β 收敛，说明中国城市全要素生产率变化随着的时间的推移波动较大，不存在明显的σ 收敛，同时，在284 个城市和三大区域城市中全要素生产率较低的城市，其全要素生产率有较高的增长速度，城市之间的全要素生产率增长差距在不断缩小，且都有向各自稳态收敛的趋势。

基于以上研究结论，主要有以下三点启示：

第一，加强城市规模效率和技术进步有助于提升城市全要素生产率，推进城乡整合和区域协调发展有助于加快城市全要素生产率变化的收敛，减少城市之间的差异。

第二，城市之间全要素生产率变化的差异受到城市产业结构和科技教育发展水平的影响，因此，地方政府部门应制定相应的产业政策，鼓励地方经济向高技术产业和第三产业转型，提升城市的产业结构水平，同时，应加大科技教育支出，鼓励加大产业、学校和研究机构联合创新，构建以市场为导向、多主体联合、产学研结合的技术创新体系，提升科研水平和科技成果转化能力。提升城市创新水平，进一步吸引人才，增加城市创新动力。

第三，本研究有待进一步研究的方向，如全市和市辖区全要素生产率变化收敛性的异质性分析和全要素生产率空间异质性分析，更深入的研究可以为驱动城乡协同和区域协同发展提供更多理论依据。