基于动态加权张量距离的多聚类算法

薛状状，李鹏，2*，樊卫北，2，张宏俊，孟凡朔

基于动态加权张量距离的多聚类算法

薛状状1，李鹏1，2*，樊卫北1，2，张宏俊1，孟凡朔1

（1.南京邮电大学 计算机学院、软件学院、网络空间安全学院，南京 210023； 2.南京邮电大学 网络安全与可信计算研究所，南京 210023）（ ∗ 通信作者电子邮箱lipeng@njupt.edu.cn）

基于张量的多聚类算法（TMC）在衡量属性重要性时忽略了对象张量内部属性组合的关联性，而且在不同的特征空间选择下，固定权重策略导致所选与未选择特征空间没有完全分离。针对上述问题，提出一种基于动态加权张量距离（DWTD）的多聚类算法（DWTD-MC）。首先，为提升各特征空间属性重要性衡量的准确性，建立了自-关联张量模型；其次，构建多视图权重张量模型，在不同特征空间选择下通过动态加权策略满足多聚类分析的需求；最后，使用DWTD衡量数据点的相似性，生成最终的多聚类结果。在真实数据集上的仿真实验结果表明，DWTD-MC在杰卡德指数（JI）、邓恩指数（DI）、DB指数（DB）和轮廓系数（SC）评价指标上均优于TMC等对比算法，而且可以在获得较高质量的聚类结果的同时，使各聚类结果之间保持较低的冗余度，满足多聚类分析的任务需求。

异构数据；多聚类；张量；张量距离；动态加权；社会物理信息系统

0 引言

随着网络化应用的发展，信息和物理系统被进一步融会贯通，网络与人类社会紧密联合，形成了融合人、机器、信息于一体的系统，即社会物理信息系统（Cyber-Physical-Social System，CPSS）［1］。从CPSS中产生了大量的多源异构数据，包括结构化、半结构化和非结构化数据。如何对这些数据进行分析，挖掘出其中潜在的知识和价值，对社会和企业有着重要意义。

聚类分析作为数据分析中的重要技术，可以揭示数据中的隐藏模式，但是单一的聚类模式难以充分挖掘出来源多样、特征高维、关系复杂的异构数据的隐藏信息。多聚类作为数据挖掘的新兴研究领域，近年来受到各领域学者的广泛关注［2］。CPSS中，从多个维度产生了大规模的多源异构数据，这些数据往往具有来源多样、类型复杂、维度高、特征模糊等特点。多聚类可以根据实际应用的不同，从数据多个角度产生多种不同的聚类结果，更深层次地揭示数据中的不同结构与隐藏信息，更好地满足当今大数据多分析任务的需求［3］。

在单聚类领域，典型的密度峰值聚类算法［4］能够高效地发掘任意形状的类簇，且不易发生错误，聚类质量较高；但算法计算复杂度较高，限制了它在大规模数据集中的应用。针对此问题，徐晓等［5］提出了一种基于网格筛选的大规模密度峰值聚类算法，使用网格化方法去除部分密度稀疏的点，可以在保证聚类准确性的基础上有效降低计算复杂度；Bo等［6］提出了一种结构化深度聚类网络将结构信息集成到深度聚类，克服了现有方法在数据结构表示方面的不足。多聚类分析的研究主要集中在多视图聚类［7］、可选择聚类［8］和子空间聚类［9］，这些方法虽然能在一定程度满足多聚类分析的需求，但也具有局限性。比如，Tzortzis等［10］提出了一种基于核的加权多视图聚类算法，该算法通过融合多源信息，从事物的不同角度生成多个特征描述视图，以此降低单个视图内的噪声，最终产生比只使用单一视图更高质量的聚类结果；但不能从多角度选择不同特征的组合产生不同的聚类结果。Yang等［11］提出了一种基于非负矩阵分解（Nonnegative Matrix Factorization， NMF）的非冗余多重聚类算法，该算法建立在NMF的基础上，利用非负性实现非冗余，能创建一个或多个高质量且彼此不同的聚类结果；但主要针对小规模、单领域数据集，不能通过结合多源信息来提高聚类质量。Gan等［12］提出了一种使用近邻传播的子空间聚类算法，该算法在近邻传播算法中引入属性权重，并根据当前分区迭代更新属性权重，以此识别嵌入簇的子空间，能够实现高维数据集聚类分析并通过提取的子空间发现良好的类簇；但是该算法不能从不同的角度产生不同的可解释的聚类结果。欧琦媛等［13］提出了一种基于压缩子空间对齐的多核聚类算法，使用线性压缩矩阵对采样过程进行建模，将采样和多核聚类任务合并到一个统一的框架，在融合多源信息提高聚类性能方面的同时大幅提高了计算效率；但只能生成单一的聚类结果。综上所述，这些多聚类算法主要针对低维、小规模、单领域数据集，它们的聚类结果难以解释，且无法根据现实需要灵活变化聚类对象生成不同的聚类结果。

Zhao等［14］提出了一种基于张量的多聚类算法（Tensor-based Multiple Clustering algorithm， TMC）能够克服上述局限性。TMC使用张量模型对异构数据进行统一表示，适用于高维、多领域的数据，使用多线性数据排名算法为多属性组合赋予权重，最后通过不同特征空间选择生成不同的聚类结果；但该算法在衡量属性重要性和固定权重策略导致的所选与未选择特征空间没有完全分离两方面存在不足。在聚类结果的评价指标领域，唐益明等［15］提出了一种新的基于数据集几何结构和大小集群的模糊聚类的有效性指标GSDC，解决了现有指标对数据结构复杂和集群大小差异悬殊的数据集难以作出精确判断的问题。严加展等［16］提出了一种改进的有效性评价指标CSC，该指标结合簇内数据平方误差和、隶属度权值等定义，能解决现有评价指标没有涉及到数据集真实几何分布结构和先验信息的问题。

为解决多聚类算法领域中，多聚类结果冗余度高、聚类结果难以解释等问题，本文在TMC的基础上提出一种基于动态加权张量距离的多聚类算法（Multiple Clustering algorithm based on Dynamic Weighted Tensor Distance，DWTD-MC）。本文的主要工作如下：

1）提出自-关联张量模型改进多线性数据排名算法，以更准确地衡量各属性的重要性。

2）构建多视图权重张量模型。在不同特征空间选择下，赋予各多属性组合对应的权重，分离各特征空间，减少未选择特征空间对已选特征空间的影响。

3）在上述两项工作基础上，提出动态加权张量距离（Dynamic Weighted Tensor Distance， DWTD）的概念，并将它作为不同数据间相似性衡量的标准。

4）在真实的数据集上进行对比实验验证，实验结果表明，DWTD-MC能够生成冗余度更低、类内结构更紧凑的多聚类结果。

1 TMC

1.1　张量与张量距离

1.1.1张量

张量理论起源于数学，在力学中有重要应用。现在，张量已成功应用于计算机视觉、图像识别等领域［17］。张量可以视为对矩阵的高阶推广。向量为一阶张量，矩阵为二阶张量，三阶或更高阶的张量称为高阶张量。

1.1.2张量距离

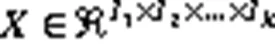
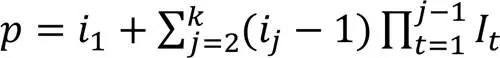
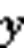
1.2　TMC

首先，使用多线性数据排名算法［19］计算各特征空间的属性排名向量，衡量特征空间属性的重要程度。该算法结合转移概率模型［20］对网页排名算法［21］的扩展。算法流程如下：

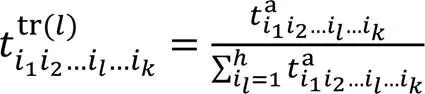
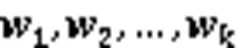
1.3　TMC的局限性

本文主要针对TMC以下两个局限性进行讨论。

1）在关联张量的构造过程中，仅考虑不同对象张量之间的各属性组合的关联性，忽视了一个对象张量内部各属性组合的关联，造成各特征空间属性权重度量不够准确。

2）在不同特征空间选择下，采用固定权重策略，忽视了不同特征空间选择的差异性，导致所选特征空间与未选特征空间没有完全分离，在衡量各属性组合重要性和对象张量之间相似性时，未选择特征空间对其他特征空间产生影响；同时固定权重会导致各聚类模式间相似度较大，多聚类结果之间冗余度过高。

2 基于动态加权张量距离的多聚类算法

针对TMC中存在的不足，本文提出了一种基于动态加权张量距离的多聚类算法DWTD-MC。首先，提出了自-关联张量衡量各对象张量之间关联，以此改进多线性数据排名算法；其次，提出多视图权重张量模型，采用动态加权策略，将各特征空间分离，降低聚类结果冗余度；最后在此基础上，使用动态加权张量距离作为对象张量相似性衡量的依据，生成多聚类结果。

2.1　动态加权张量距离模型构建

2.1.1自-关联张量模型

图1　三阶对象张量

2.1.2多视图权重张量模型

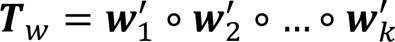
图2　三阶权重张量

算法1 多视图权重张量算法。

repeat

end for

for=1 todo

end for

2.1.3动态加权张量距离

张量距离能够有效衡量高阶空间对象之间的相似度，但根据相关定义可知，在张量距离中，坐标对应的属性组合被认为是同等重要的，并且反映元素位置内在关系的度量系数是固定的。这使张量距离的概念不能降低噪声属性的影响，同时不能满足多聚类分析的任务需求。而在TMC中，通过给属性组合添加权重因子能有效降低噪声属性的影响，但固定的加权策略忽视了不同特征空间选择之间的差异，也使聚类性能较差。基于此问题，本文提出动态加权张量距离的概念，在张量距离中引入特征空间选择向量和动态权重因子，可以根据情境选择特征空间进行多聚类分析，同时降低噪声属性的影响以及多聚类结果之间的冗余度。

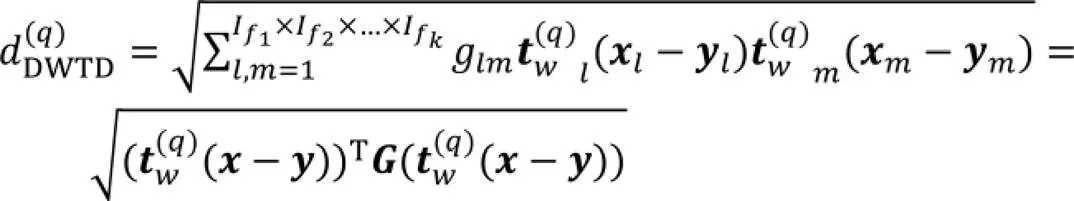
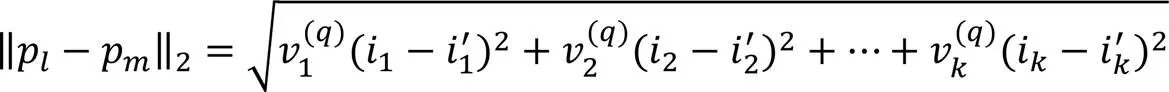
2.2　多视图相似度矩阵张量模型构建

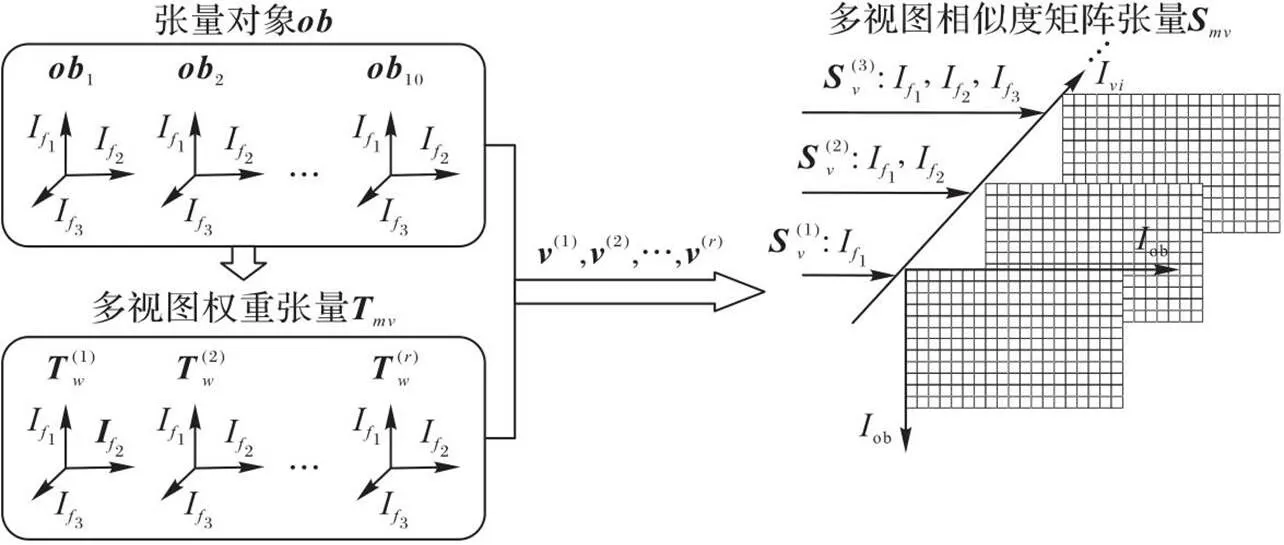
图3　多视图相似度矩阵张量

2.3　算法流程

基于上述介绍的理论和模型，本文结合密度峰值聚类算法，提出了基于动态加权张量距离的多聚类算法DWTD-MC。

算法2 基于动态加权张量距离的多聚类算法。

for=1 todo

end for

end for

end for

end for

end for

3 实验与结果分析

本章对DWTD-MC进行实验分析，并与以下算法进行比较：TMC、使用不加权的张量距离衡量相似性的多聚类算法（Multiple Clustering algorithm based on Non-Weighted Tensor Distance， NWTD-MC）［14］和基于张量分解的多聚类算法（Multiple Clustering algorithm based on Tensor Decomposition， TD-MC）［23］。

3.1　复杂度分析

3.2　数据集

本文使用真实数据集进行实验，数据集分别为：1）气候数据集（包括广州、北京、上海等地区气候状况），每条记录包括天气状况、温度、湿度特征（记录范围分别为晴/多云/阴/雨、［21，33］℃、［35，98］%rh），后文记为数据集1；2）空气质量数据集（包括多地空气质量状况），每条记录包括PM2.5、SO2、NO2、O3等特征，后文记为数据集2，它的详细信息见表1。通过不同的特征选取与聚类分析，可以将在此特征上相似度较高的地区进行分组，生成多聚类结果。

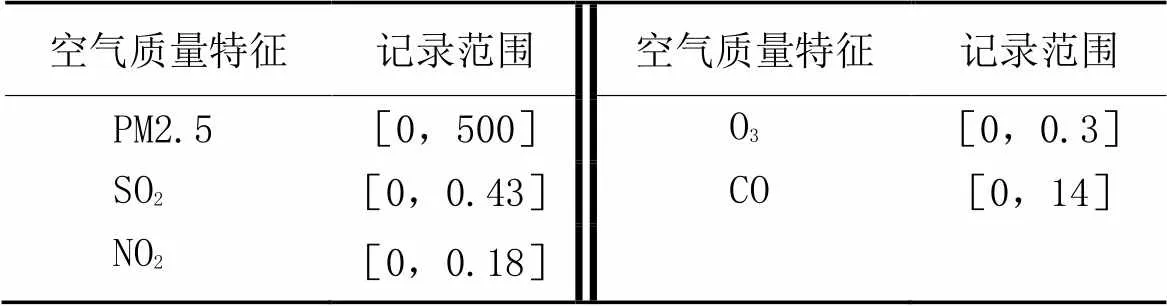
表1　空气质量数据集特征 单位： mg/m3

3.3　评价指标

评价指标的选取依据：1）对不同的聚类结果之间冗余度进行评价，分析算法在多聚类方面的性能；2）对各聚类结果的内部质量进行评价，分析算法的聚类性能。

1）杰卡德指数（Jaccard Index，JI）。JI用来度量两种不同聚类结果之间的相似性，衡量聚类结果之间的冗余度［24］。假设和是两种不同的聚类结果，JI定义如下：

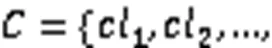
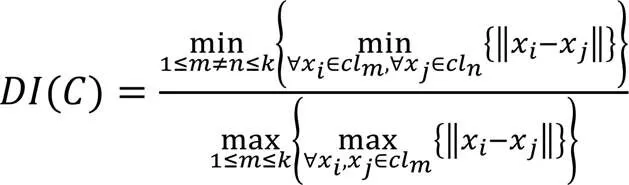
其中：分子部分是一种类间间距度量，表示不同类簇中数据点间的最小距离；分母是一种类内间距度量，表示同一类簇中数据点间的最大距离。根据式（18），DI值越大，表示类内越紧凑，类与类之间越能区分开，聚类质量越好。

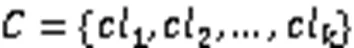
其中：avg（cl）、avg（cl）表示对应类簇内，样本间的平均距离；den（cl，cl）表示两个类簇中心点间的距离。根据式（19），DB值越小，表明不同类簇间分离度更好。

4）轮廓系数（Silhouette Coefficient， SC）。SC是所有样本轮廓系数的平均值，定义如下：

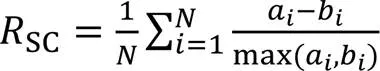
3.4　结果分析

首先对数据进行预处理：

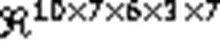
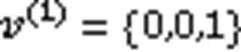
图6、7分别为数据集1和数据集2上的DI值， 其中：图6横轴的A～G分别表示特征空间选择向量｛0，0，1｝、｛0，1，0｝、｛1，0，0｝、｛0，1，1｝、｛1，0，1｝、｛1，1，0｝、｛1，1，1｝；图7横轴的A～G分别表示特征空间选择向量｛1，0，1，0，1｝、｛1，1，0，1，0｝、｛1，1，1，0，0｝、｛1，1，0，1，1｝、｛1，0，1，1，1｝、｛1，1，1，1，0｝、｛1，1，1，1，1｝。从直方图可以看出，DWTD-MC的DI值大多高于TMC、NWTD-MC与TD-MC。但也出现了部分DWTD-MC的DI值略低的情况，分析其原因：在此种聚类模式下，数据分布较为均匀，类簇与类簇之间划分不够明显，导致DI值较低。从表2中4组实验的平均DI值可以看出，DWTD-MC的平均DI值都相对较高。DWTD-MC通过动态地添加权重，将特征空间完全分离，区分了不同特征空间选择下，多属性组合重要程度的不同，降低了噪声属性的影响，最终提高了聚类结果的质量。

从表2中4组实验的平均DB值和平均SC值可知，DWTD-MC生成的聚类结果中不同类簇间分离度更好，同一类簇内更为紧凑。

综上所述，相较于TMC、NWTD-MC与TD-MC，DWTD-MC所产生的多聚果之间有着更低的冗余度，产生的聚类结果更为丰富，同时每种聚类结果的类内结构也更紧凑，聚类结果质量更高。

图5　数据集2上的JI值

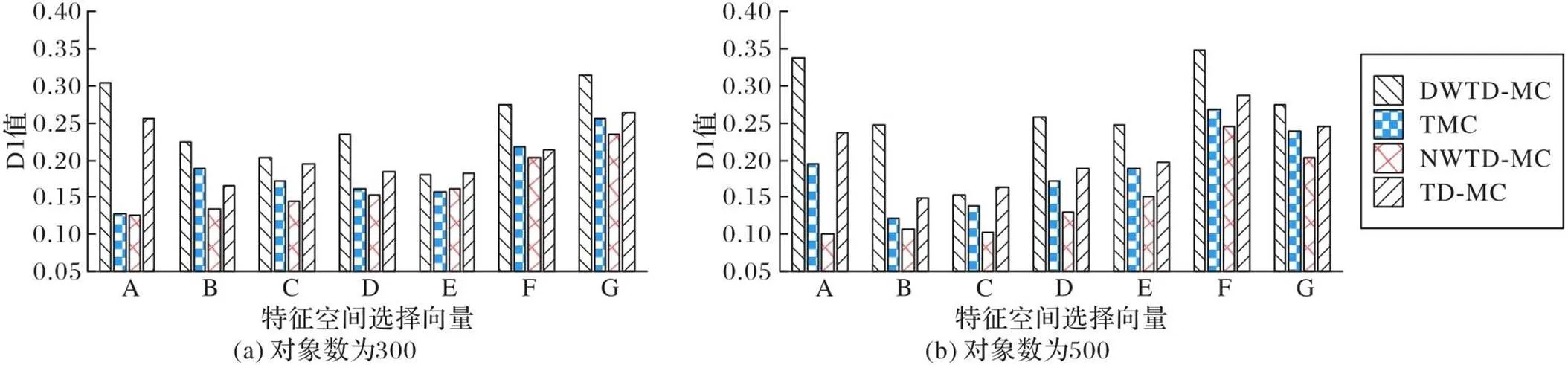
图6　数据集1上的DI值

图7　数据集2上的DI值

表2　指标平均值统计表

4 结语

本文针对TMC中关联张量模型无法准确衡量属性重要性，特征空间未完全分离导致的聚类结果冗余度高、质量差的问题，提出了一种基于动态加权张量距离的多聚类算法（DWTD-MC）。实验结果表明，DWTD-MC具有更好的聚类效果。但该算法中，使用张量模型统一表示异构数据时，并不能适用于所有种类的数据；聚类分析时仅将数据对象间的距离作为相似度衡量的依据，指标单一可能会使得聚类结果不够准确；在多视图相似度矩阵张量的构建过程与密度峰值聚类算法中，涉及到大量的张量、矩阵运算，这导致该算法的计算复杂度较高，影响算法的效率。因此，下一步要研究如何更全面表示多源异构数据，多角度衡量数据对象相似度，以及从并行化等角度提高计算效率的方法。

[1] ZHOU Y， YU F R， CHEN J， et al. Cyber-physical-social systems： a state-of-the-art survey， challenges and opportunities［J］. IEEE Communications Surveys and Tutorials， 2020， 22（1）： 389-425.

[2] MÜLLER E， ASSENT I， GÜNNEMANN S， et al.special issue on discovering， summarizing and using multiple clusterings［J］. Machine Learning， 2015， 98（1/2）： 1-5.

[3] WANG J， WANG X， YU G， et al. Discovering multiple co-clusterings with matrix factorization［J］. IEEE Transactions on Cybernetics， 2021， 51（7）： 3576-3587.

[4] RODRIGUEZ A， LAIO A. Clustering by fast search and find of density peaks［J］. Science， 2014， 344（6191）： 1492-1496.

[5] 徐晓，丁世飞，孙统风，等. 基于网格筛选的大规模密度峰值聚类算法［J］. 计算机研究与发展， 2018， 55（11）： 2419-2429.（XU X， DING S F， SUN T F， et al. Large-scale density peaks clustering algorithm based on grid screening［J］. Journal of Computer Research and Development， 2018， 55（11）： 2419-2429.）

[6] BO D， WANG X， SHI C， et al. Structural deep clustering network［C］// Proceedings of the 2020 Web Conference. Republic and Canton of Geneva： International World Wide Web Conferences Steering Committee， 2020： 1400-1410.

[7] LIU X， JI S， GLÄNZEL W， et al. Multiview partitioning via tensor methods［J］. IEEE Transactions on Knowledge and Data Engineering， 2013， 25（5）： 1056-1069.

[8] HE T， ONG Y S， HU P. Multi-source propagation aware network clustering［J］. Neurocomputing， 2021， 453： 119-130.

[9] ELHAMIFAR E， VIDAL R. Sparse subspace clustering： algorithm， theory， and applications［J］. IEEE Transactions on Pattern Analysis and Machine Intelligence， 2013， 35（11）： 2765-2781.

[10] TZORTZIS G， LIKAS A. Kernel-based weighted multi-view clustering［C］// Proceedings of the IEEE 12th International Conference on Data Mining. Piscataway： IEEE， 2012： 675-684.

[11] YANG S， ZHANG L. Non-redundant multiple clustering by nonnegative matrix factorization［J］. Machine Learning， 2017， 106（5）： 695-712.

[12] GAN G， NG M K P. Subspace clustering using affinity propagation［J］. Pattern Recognition， 2015， 48（4）： 1455-1464.

[13] 欧琦媛，祝恩. 基于压缩子空间对齐的多核聚类算法［J］. 计算机工程与科学， 2021， 43（10）： 1730-1735.（OU Q Y， ZHU E. Multi-kernel clustering algorithm based on compressed subspace alignment［J］. Computer Engineering and Science， 2021， 43（10）： 1730-1735.）

[14] ZHAO Y， YANG L T， ZHANG R. A tensor-based multiple clustering approach with its applications in automation systems［J］. IEEE Transactions on Industrial Informatics， 2018， 14（1）： 283-291.

[15] 唐益明，丰刚永，任福继，等. 面向结构复杂数据集的模糊聚类有效性指标［J］. 电子测量与仪器学报， 2018， 32（4）：119-127.（TANG Y M， FENG G Y， REN F J， et al. Fuzzy clustering validity index facing data set with complexity structure［J］. Journal of Electronic Measurement and Instrumentation， 2018， 32（4）： 119-127.）

[16] 严加展，陈华，李阳. 改进的模糊C-均值聚类有效性指标［J］. 计算机工程与应用， 2020， 56（9）： 156-161.（YAN J Z， CHEN H， LI Y. Improved fuzzy C-means clustering validity index［J］. Computer Engineering and Applications， 2020， 56（9）： 156-161.）

[17] KOLDA T G， BADER B W. Tensor decompositions and applications［J］. SIAM Review， 2009， 51（3）： 455-500.

[18] LIU Y， LIU Y， CHAN K C C. Tensor distance based multilinear locality-preserved maximum information embedding［J］. IEEE Transactions on Neural Networks， 2010， 21（11）： 1848-1854.

[19] 匡立伟. 基于张量的大数据统一表示及降维方法研究［D］. 武汉：华中科技大学， 2016： 32-35.（KUANG L W. A tensor-based approach for united representation and dimensionality reduction of big data［D］. Wuhan： Huazhong University of Science and Technology， 2016： 32-35）

[20] JOSE M， MARTINEZ V， REINALDO A， et al. On the limiting probabilities of theM/E/1 queueing system［J］. Statistics and Probability Letters， 2014， 88： 56-61.

[21] GUO P-C， GAO S-C， GUO X-X. A modified newton method for multilinear PageRank［J］. Journal of Mathematics， 2018， 22（5）： 1161-1171.

[22] KUANG L， HAO F， YANG L T， et al. A tensor-based approach for big data representation and dimensionality reduction［J］. IEEE Transactions on Emerging Topics in Computing， 2014， 2（3）： 280-291.

[23] ZHAO Y， YANG L T， ZHANG R. Tensor-based multiple clustering approaches for cyber-physical-social applications［J］. IEEE Transactions on Emerging Topics in Computing， 2020， 8（1）： 69-81.

[24] LIU S， ZHENG J， LIN Q， et al. Evolutionary multi and many-objective optimization via clustering for environmental selection［J］. Information Sciences， 2021， 578： 930-949.

[25] ZHENG X， LIU X， CHEN J， et al. Adaptive partial graph learning and fusion for incomplete multi-view clustering［J］. International Journal of Intelligent Systems， 2022， 37（1）： 991-1009.

Multiple clustering algorithm based on dynamic weighted tensor distance

XUE Zhuangzhuang1， LI Peng1，2*， FAN Weibei1，2， ZHANG Hongjun1， MENG Fanshuo1

（1，，210023，；2，，210023，）

When measuring the importance of attributes in Tensor-based Multiple Clustering algorithm （TMC）， the relevance of attribute combinations within object tensors are ignored， and the selected and unselected feature space are incompletely separated because of the fixed weight strategy under different feature space selection. For above problems， a Multiple Clustering algorithm based on Dynamic Weighted Tensor Distance （DWTD-MC） was proposed. Firstly， a self-association tensor model was constructed to improve the accuracy of attribute importance measurement of each feature space. Then， a multi-view weight tensor model was built to meet the task requirements of multiple clustering analysis by dynamic weighting strategy under different feature space selection. Finally， the dynamic weighted tensor distance was used to measure the similarity of data points， generating multiple clustering results. Simulation results on real datasets show that DWTD-MC outperforms comparative algorithms such as TMC in terms of Jaccard Index （JI）， Dunn Index （DI）， Davies-Bouldin index （DB） and Silhouette Coefficient （SC）. It can obtain high quality clustering results while maintaining low redundancy among clustering results， as well as meeting the task requirements of multiple clustering analysis.

heterogeneous data; multiple clustering; tensor; tensor distance; dynamically weighting; Cyber-Physical-Social System (CPSS)

1001-9081（2023）11-3449-08

10.11772/j.issn.1001-9081.2022101626

2022⁃11⁃09；

2022⁃12⁃29；

国家自然科学基金资助项目（62102194）； 江苏省“六大人才高峰”高层次人才项目（RJFW⁃111）。

薛状状（1997—），男，江苏睢宁人，硕士研究生，主要研究方向：机器学习、多聚类算法； 李鹏（1979—），男，福建长汀人，教授，博士，CCF会员，主要研究方向：计算机通信网络、无线传感器网络、信息安全； 樊卫北（1987—），男，河南开封人，讲师，博士，CCF会员，主要研究方向：并行和分布式系统、数据中心网络、云计算； 张宏俊（1985—），男，安徽皖和人，博士研究生，主要研究方向：基于张量链分解的多聚类及并行优化； 孟凡朔（1997—），男，江苏徐州人，硕士研究生，主要研究方向：张量链式分解。

TP181

A

2023⁃01⁃03。

This work is partially supported by National Natural Science Foundation of China （62102194）， “Six Talent Peaks” High-level Talents Project of Jiangsu Province （RJFW-111）.

XUE Zhuangzhuang， born in 1997， M. S. candidate. His research interests include machine learning， multiple clustering algorithm.

LI Peng， born in 1979， Ph. D.， professor. His research interests include computer communication networks， wireless sensor networks， information security.

FAN Weibei， born in 1987， Ph. D.， lecturer. His research interests include parallel and distributed systems， data center network， cloud computing.

ZHANG Hongjun， born in 1985， Ph. D. candidate. His research interests include multiple clustering and parallel optimization based on tensor chain decomposition.

MENG Fanshuo， born in 1997， M. S. candidate. His research interests include tensor chain decomposition.