针对大规模两重互异性矩形件组批排样方法*

邵柏岩,叶伯生,王宏磊,梁 广

(1.华中科技大学机械科学与工程学院,武汉 430074;2.北京化工大学数理学院,北京 100029;3.哈尔滨工业大学深圳校区机电工程与自动化学院,深圳 518055)

0 引言

矩形排样是一类经典的优化问题,其目的是合理规划矩形件在板材上的布局,以提高板材利用率、简化切割过程、保障加工质量。矩形排样常见于智能制造[1]、皮革剪裁[2]、家具加工[3]、玻璃切割[4]、钣金加工[5]等方面,是制造业自动化的关键环节,直接影响加工的成本与质量。求解该问题的方法主要分为3类:确定性算法、启发式算法和智能优化算法。最初,不少学者通过数学规划尝试给出该问题的精确解,这些方法对小批量排样问题有不错的效果。但在此之后,矩形排样被数学家证明是NP-Hard 问题,加之生产力的迅猛发展,企业常有对大规模订单加工的现实需求,两者之间的矛盾,迫使学者们转向寻找可以高效求解矩形排样问题近似解的算法。先后出现了BLF、最低水平线[6]、剩余矩形匹配[7]等诸多启发式算法,这些方法的主要思想是将矩形件按一定的规则和顺序进行排样。在面对大规模订单时可以快速的给出排样方案,但由于算法相对简单,求解出的板材利用率有待提高。随着智能优化算法的兴起,学者们利用改进后的邻域搜索算法[8]、蚁群算法[9]、模拟退火算法[10]、遗传算法[11-12]等对矩形排样问题进行求解,实验表明效果比原有算法有一定的提升。但大多数智能算法都要对样本进行反复迭代,算法内存在大量待调参数,使得智能算法在面对大规模订单时不仅求解时间过长,而且求解结果太过依赖于初始参数的选取,常出现结果不稳定或过早收敛现象。

当今注重个性化定制,待加工的订单中矩形件形状和所用材料均存在强互异性。但现有研究均是针对形状强互异性,鲜有研究考虑到所用材料的强互异性。针对此类大规模两重互异性问题,本文首先在现有研究基础上提出了一种稳定性好、高效快捷、板材利用率高的大规模排样算法,即带对偶项的降序有限首次适应算法来解决形状强互异性的问题。再进一步对订单组批问题加以研究,量化描述订单所用材料的相似度,通过对每个订单材料相似度以及工厂产能限制、生产效率等因素综合考量,提出了考虑材料相似度的二阶段贪心算法。通过该算法将总订单依材料的相似程度组成若干批次,再对每个批次进行排样加工来最大程度规避材料强互异性对板材利用率的影响。最后,利用多个测试数据集来验证算法的有效性。

1 形状强互异性的矩形件排样算法

1.1 数学模型的建立

1.1.1 排样过程命名约定

在矩形排样的过程中,考虑到加工的便利性与可靠性,采用三阶段齐头切精确排样[13],故加工中只会出现3种形式:对板材进行第1阶段切割得到的条带(stripe),对条带进行第2阶段切割得到的堆栈(stack),对堆栈进行第3阶段切割得到最终的产品项(item)。切割后不能成为完整产品项的部分视为废料(wasted)。为方便建立数学模型,对整个排样过程中各部分的命名进行约定:

如图1所示,对于一块待切割板材,可以视作由若干个产品项及未利用的部分组成的集合,其中产品项i的长度为li,不妨让产品根据其长度从高到低的顺序进行排序:

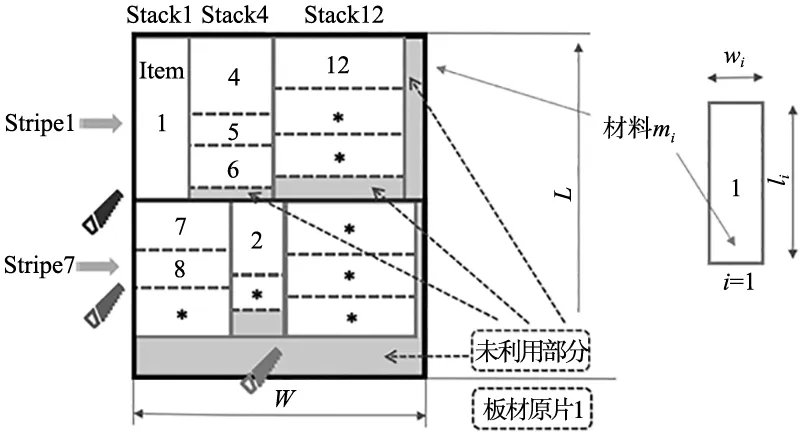
图1 命名约定示意图

l1≥l2≥…≥ln

(1)

规定了产品项的编号后,进一步定义堆栈、条带和板材的编号。采用文献[14]的方式,将堆栈中包含的长度最长的产品项所对应的编号定义为该堆栈的编号,即堆栈的编号是其所包含产品项中的最小编号。以此类推,条带的编号是其所包含堆栈中的最小编号,而板材的编号是其所包含条带中的最小编号。另外,规定板材按照水平、竖直、水平3个阶段依次进行切割。

1.1.2 多约束混合整数规划模型

对矩形排样优化问题,建立多约束混合整数规划模型。首先引入0～1变量为:

(2)

式中:αj,i=1当且仅当产品项i包含在堆栈j中,βk,j=1当且仅当堆栈j包含在条带k中,γh,k=1当且仅当条带k包含在板材h中。

可以注意到,遵从上述命名约定的情况下,如果板材h存在,那么板材h一定包含编号为h的条带、堆栈及产品项,且产品项h为板材h中编号最小的产品项。此时有:

γh,h=1,h∈{1,…,n}

(3)

由于板材利用率等于产品项总面积与所需板材总面积之比,最大化板材利用率等价于最小化板材使用数量,故矩形排样优化的整数规划模型为:

(4)

subject to:

(5)

αj,i=0,∀i>jorwi≠wjorli+lj>L

(6)

(7)

(8)

(9)

(10)

(11)

式(5)表示产品唯一性约束:每个产品项i有且仅有一个,因此每个产品项只能包含在一个堆栈中。式(6)表示堆栈同宽限长:根据三阶段齐头切精确排样要求,同一堆栈中产品项的长度或宽度相同且均与堆栈的宽度相同,同时任意产品项长度之和必须小于等于板材长度。式(7)表示堆栈唯一性:如果堆栈j存在,则该堆栈只能被包含在一个条带中。式(8)表示条带唯一性:如果条带k存在,则该条带只能被包含在一个板材中。式(9)表示条带长度约束:同一个条带中任意堆栈的产品项长度之和小于等于该条带长度。式(10)表示板材总宽度约束:同一个条带中的堆栈宽度之和小于等于板材宽度。式(11)表示板材总长度约束:同一个板材中的条带长度之和小于等于板材长度。

注意到,将产品项旋转90°并不会改变产品的本质,但是上述模型只考虑了产品不旋转的情形,下面改进模型来将旋转的情形考虑进去。

产品项具有不同的属性,包括编号、材料、长度、宽度和所属订单。产品旋转90°意味着将项目的长度与宽度互换。于是,对产品项i,若产品项i*满足其长度等于i的宽度,宽度等于i的长度,且其他属性完全相同,则将产品项i*称为产品项i的对偶项目。

将所有产品项的对偶项目作为虚拟项目引入规划,此时项目数等于原项目的2倍,即n′=2n。令i+n为i的对偶项目。于是改进后的数学模型只需要在原有基础上增添一个新的约束条件,称其为对偶约束:

(12)

1.2 带对偶项的降序有限首次适应算法

基于文献[14]中提出的有限首次适应算法(finite first fit algorithm,FFF),将对偶项考虑进去,并引入同宽产品聚集概率对FFF算法进行改进,提出了带对偶项的降序有限首次适应算法(descending finite first fit algorithm-dual,DFFF-dual)。

FFF算法,首先根据输入产品项列表的长度和宽度进行降序排列。然后顺序遍历所有产品,将产品项装入一个空的堆栈中并从产品项列表中删除已装入的产品项。然后通过一个概率阈值P(称为同宽产品聚集概率)来决定是否继续遍历寻找宽度相同的产品项放入同一堆栈中。后续将通过对概率阈值参数P寻优来进一步优化算法。当一个堆栈装满了所需的产品项后,生成一个长度与该堆栈相同的新条带来将其装入。在该新条带中生成一个新的空堆栈,按上述方式去遍历并装入新的产品项。以此类推,会得到被装满的条带,多条同样被装满的条带就会组成一块被装满的板材。如此循环,最终会得到包含数据集中所有产品项的板材合集,每块板材上有对应的产品排样方案,所有板材及对应的排样方案组成了输入数据集的最终排样方案。

DFFF-dual算法的实现流程大体与FFF相同。首先合并产品项列表和对应的对偶项列表,然后根据新列表降序排序。而在顺序遍历的过程中,删去产品项时连同其对偶项一并删去,其他排样过程与FFF算法相同,就可以得到DFFF-dual算法,算法的伪代码如表1所示。

表1 带对偶项的降序有限首次适应算法(DFFF-dual)

在算法中,P称为同宽聚集概率,表示相同宽度的产品出现在同一个堆栈的可能性。通过实验对概率值进行寻优,发现概率越小求解出的利用率越高,当P=0时,板材利用率较高。

2 材料强互异性的订单组批算法

2.1 多约束混合整数规划模型的建立

订单组批优化是在排样前,依据工厂产能等约束条件将总订单合理的分成若干加工批次,以提高生产效益的过程。可见它是排样加工的准备工作,要建立组批问题的数学模型,关键是在原有基础上添加下列约束条件:

(1)板材h只能在一个批次中,故有约束条件:

(13)

式中:ηq,h取值范围为{0,1},ηq,h=1当且仅当板材h包含在批次q中。

(2)相同订单的项目只能在同一批次处理,记:

(14)

则ξq,i=1当且仅当项目i在批次q中。设oi表示产品i的所属订单,注意到:

项目i,j都在批次q中等价于ξq,i=1∧ξq,j=1,等价于ξq,iξq,j=1,经推导该约束可写作:

(15)

(3)同一块板材上的产品项的材质必须相同,记:

(16)

则ψh,i=1当且仅当项目i在板材h上。设mi表示产品i的材料,于是该约束等价于:

(ψh,iψh,j=0∨mi=mj),i=1,…,n,j=1,…,n,h=1,…,n

(17)

(4)每批次加工的产品项个数要小于数量限制nm:

(18)

(5)每批次加工的产品项总面积要小于产能限制Sm:

(19)

于是,订单组批问题的混合整数规划模型为:

(20)

s.t. (5)(6)(7)(8)(9)(10)
(11)(12)(14)(16)(18)(19)

αj,i∈{0,1},j=1,…,n,i=j,…,n
βk,j∈{0,1},k=1,…,n,j=k,…,n
γh,k∈{0,1},h=1,…,n,k=h,…,n
ηq,h∈(0,1),q=1,…,n,h=q,…,n

2.2 二阶段贪心算法

设计模型的求解算法,只需要对总产品项列表做划分,其每个划分出的子项目列表都满足上述约束,再对每个子项目列表应用排样算法,就可以得出组批及排样结果。

为了保证交货期,要求订单相同的项目一定在同一批次中,于是可以采用二阶段贪心算法在保证约束条件的前提下不断地将某个订单的项目放入子项目列表,直到放不下为止,其算法流程如表2所示。

表2 二阶段贪心算法

同其他贪心算法类似,并在第3步之前,对订单列表依项目数进行排序,先处理规模大的订单,再处理小订单,所得的结果会更优良。

2.3 考虑相似度的二阶段贪心算法

对上述二阶段贪心算法求解的结果进行分析发现,由于订单中产品项除形状外,每个订单所用到的材料也具有强互异性。材料差异将导致一个加工批次常出现某种材料的板材上只有少数几个产品,这会大幅降低板材利用率。为使利用率最大化,要让材料相同的项目尽可能在同一批次中进行加工。这意味着,在“贪心”地选取订单的时候,要注意待选订单与已选订单所用材料的相似程度。优先选择材料相似度高的订单,最好是被包含在已有订单的材料集合中,这样可以让材料相同的产品项尽可能的凑在一起,以此提高板材的利用率。

为定量衡量订单所用材料的相似程度,对订单的材料相似度进行定义。记m(o)表示订单o中所有项目所用材料构成的集合。对订单集A={o1,o2,…,oq},记m(A)=∪o∈Am(o)。于是可以定量描述两个订单集A、B的材料相似度:R(A,B)=|m(A)∩m(B)|/|m(A)∪m(B)|。

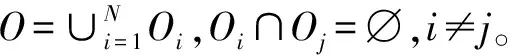
(21)

记t(o)为订单o的所有项目构成的集合,对订单集A,记t(A)=∪o∈At(o),于是组批问题中的约束(18)就变成了|t(Oi)|≤nm,i=1,…N。再记l(t)、w(t)分别表示项目t的长度和宽度,则约束(19)就变为:

(22)

于是,二阶段算法中第一阶段的数学模型为求订单集O的一个划分O1,O2,…,ON,使得:

(23)

subject to: (22) (24)

|t(Oi)|≤nm,i=1,…,N

(24)

在将订单之间材料相似度纳入考虑后,对上述二阶段贪心算法加以改进提出考虑相似度的二阶段贪心算法,其具体流程如表3所示。

表3 考虑材料相似度的二阶段贪心算法

3 实验与分析

现有矩形排样测试数据集所含的产品项数量都较少,并且所用材料都是相同的,不符合大规模个性化订单形状、材料两重强互异性的特点。所以,在进行实验验证时选用2022年中国研究生数学建模竞赛提供的工厂生产过程中真实的订单数据集作为实验对象。其中A1～A4数据集均包含800个左右形状存在强互异性的待加工矩形件;B1～B5每个数据集包含20 000～30 000个形状、材料都存在强互异性的待加工矩形件,适合于算法的验证。

3.1 矩形排样实验验证

在此假定每块板材的规格不变L×W=2440 mm×1220 mm,用DFFF-dual算法和文献[14]中FFF算法分别对数据集A的4个子数据集进行求解,并将两个算法求解的结果在表4中进行对比。

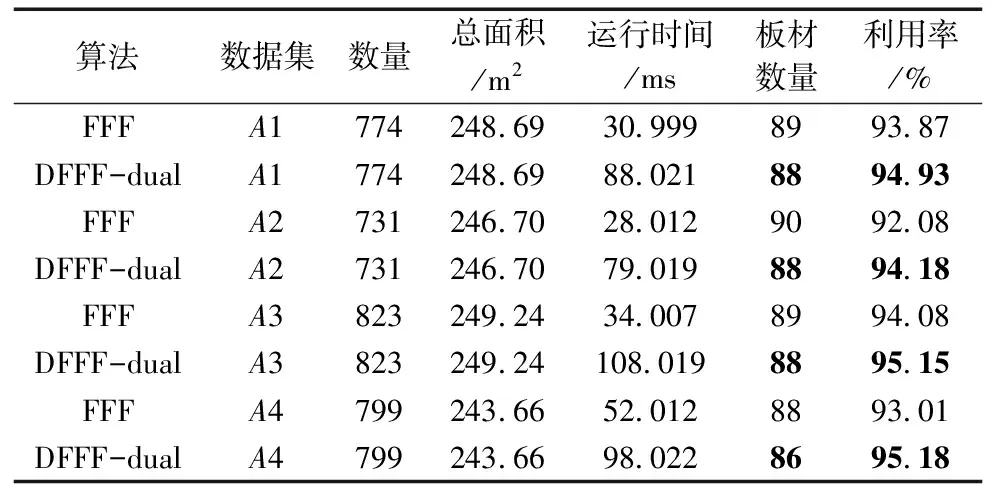
表4 FFF与DFFF-dual对A数据集求解结果对比

由于订单规模庞大,在此从A1、A2中各随机选取10个DFFF-dual算法求解的排样效果图进行范例展示,如图2和图3所示。

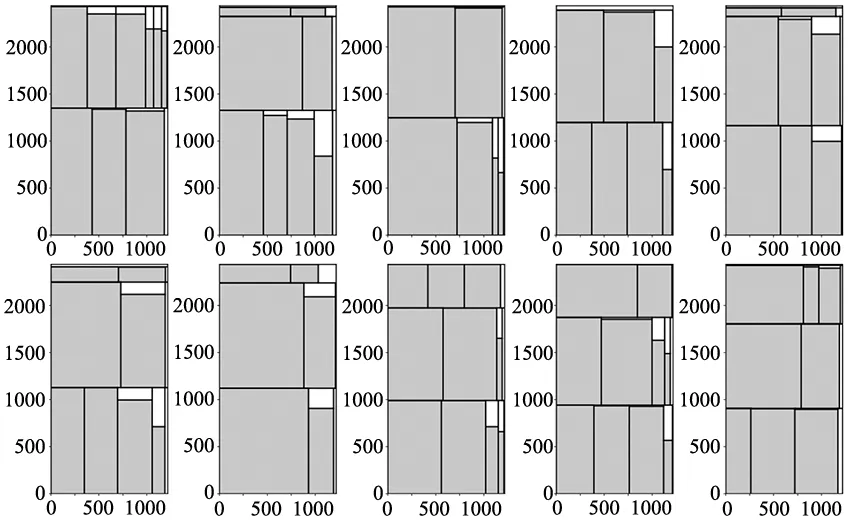
图2 数据集A1的部分排样效果图

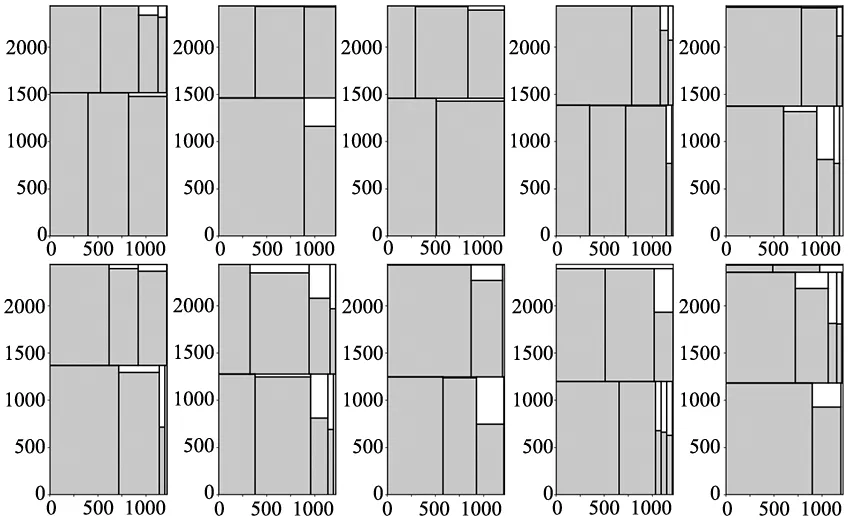
图3 数据集A2的部分排样效果图

3.2 矩形排样实验结果分析

通过DFFF-dual算法求解出的排样方案相比于FFF算法有2%的提升,并且板材的利用率可以高达95%左右,可以满足实际加工生产的要求。不仅如此,算法对数据集求解的时长均在1 s以内,由此证明DFFF-dual是求解排样问题快速高效的算法。通过观察数据集求解结果表格,对比FFF和DFFF-dual的输出结果和利用率可以得出结论:

(1)从板材原片利用率上看,DFFF-dual算法优于FFF算法,并且样本数量越大,样本形状越复杂多样,DFFF-dual算法求解结果相较FFF算法提升会越大;

(2)从算法时间复杂度上看,FFF算法优于DFFF-dual算法,DFFF-dual运行时间大致为FFF的2～3倍,这是由于引入对偶项目引起的。但两个算法的求解时长都在毫秒级别,对求解效率的影响可以忽略。

3.3 订单组批实验验证

以数据集B1～B5为对象进行实验验证,同样约定每块板材的规格不变。另外,假定单个批次产品项总数上限nm=1000,单个批次产品项的面积总和上限Sm=2502。分别使用TSG和TSG-S算法对数据集进行组批优化,得到不同批次的订单列表,之后均用DFFF-dual算法对每个单独批次的产品数据列表进行排样优化,得到组批排样方案。两个算法组批并排样的结果对比如表5所示。

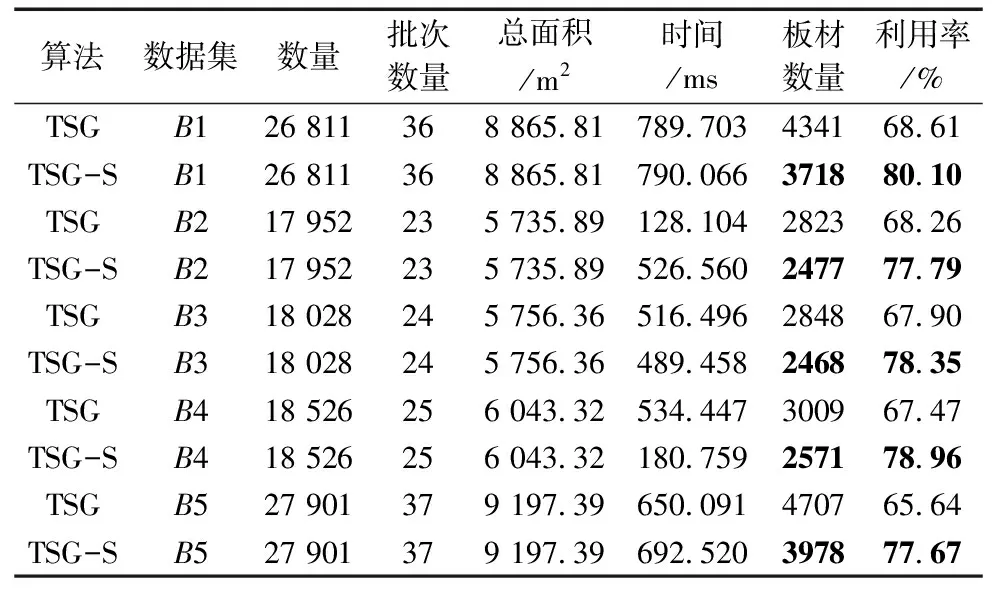
表5 TSG与TSG-S对B数据集求解结果对比

由于数据集B求解得到的图示数量庞大,故在此从B1、B3中各随机选取10个用TSG-S算法组批、用DFFF-dual算法排样的示意图进行范例展示,如图4和图5所示。

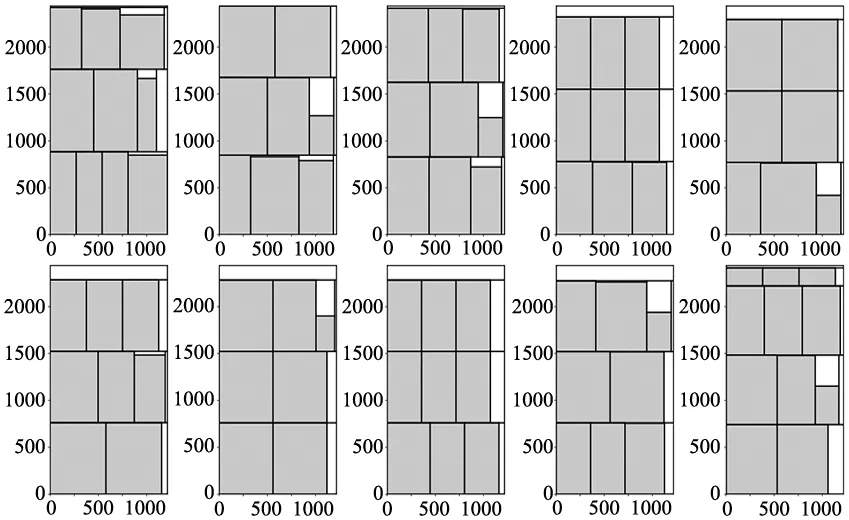
图4 数据集B1的部分排样效果图

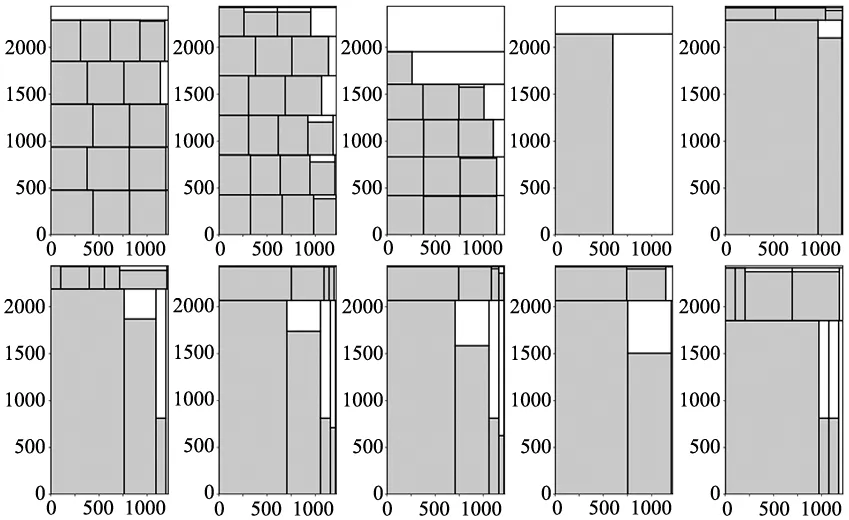
图5 数据集B3的部分排样效果图

3.4 订单组批实验结果分析

通过对比表4中两种组批优化算法的结果,可以发现,在使用相同排样优化算法的情况下,TSG-S算法的效果要远远优于TSG算法,每个数据集的利用率都能提高11%～12%,这说明了在组批优化问题中,用本文提出的方法将订单所用材料的相似度定量考虑进去后,能够大幅度减少每个批次中所使用板材的数量,提高利用率。

对两种组批优化算法的相似度矩阵进行可视化,绘制如下相似度热力图,如图6所示。

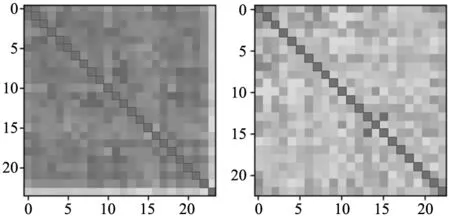
图6 TSG及TSG-S的相似度矩阵热力图

颜色越深相似度矩阵中所对应的数值越大。可以看出,TSG算法比TSG-S算法颜色深,这表明后者对组批优化问题数学模型的求解效果更加好,这与实际运行出的结果相一致,直观显现出TSG-S算法的优势。

4 结论

针对形状强互异性问题,本文在现有FFF排样优化算法的基础上,将旋转的情况纳入考虑,并引入同宽产品聚集概率对其进行改进,提出适用于三阶段齐头切精确排样的DFFF-dual算法。DFFF-dual算法优化效果相较性能优良的FFF算法还要有显著的提升。在对数据集A进行实验验证时,平均求解时长在100 ms以内,比现有的传统算法、启发式算法都快。并且,在保证速度的同时又不失性能,在测试的4个数据集上,板材利用率可达95%左右。

针对材料强互异性问题,提出定量描述订单之间材料相似度的方法,将所用材料相近的订单最大程度组合进同一加工批次,由此得到TSG-S算法。通过实验验证,使用TSG-S算法对数据集B进行组批优化后,再对每个批次使用DFFF-dual算法进行排样优化,最终板材利用率最高可以达到80.10%,TSG-S算法相较于TSG算法的性能提升了11%～12%。

综上所述,本文提出的DFFF-dual和TSG-S算法在解决大批量两重互异性矩形件组批排样优化问题上效果显著,对于实际生产活动具有指导意义。