基于遗传算法的高速永磁电机联合仿真优化*

周大伟,陆 丽,杨长青,代 阳,汪 夕

(上海电机学院电气学院,上海 201306)

0 引言

随着政策的提出,在工业、交通和生活等领域以体积小、重量轻、高可靠性和高功率密度为特点的永磁同步电机得到了快速发展[1-2]。因为永磁同步电机的转子侧永磁体提供磁势源,使此类电机功率密度大,允许的气隙大,非常适合高速运行[3]。

通常将电机转速10 000 rpm以上或者功率与转速的乘积大于1×105的电机称为高速永磁同步电机(HSPMSM)[4]。电机转速过高会使电机频率大幅增大,导致电机磁场谐波含量增多,容易导致电机产生较大的振动噪声[5]。同时,电机高转速也会使转子受到的离心力较大,对电机转子动力学的性能也提出来较高的要求,因此对于HSPMSM的优化至关重要,需要满足电机高转速性能的同时降低电机高速状态下的转矩脉动和齿槽转矩,改善由于电机高频率带来的振动噪声。

国内外学者对HSPMSM的优化方法研究主要采用传统磁路计算法、有限元法和田口法等。邱马顺等[6]以高速电机额定转矩、转矩脉动和磁密为优化目标,采用了田口迭代法研究了电机定转子结果参数对上述性能的影响。张娣等[7]为提高高速永磁同步电机性能,运用有限元法以隔磁桥和永磁体厚度为优化变量对电机进行参数优化,得到了这两个参数的最优解。周凤争等[8]以一台2.3 kW的高速永磁无刷直流电机为研究对象,讨论了不同转子充磁和支撑结构对电机气隙磁密和齿槽转矩的影响,结果表明电机平行充磁方式的磁密谐波含量低于径向充磁方式,有效削弱了电机齿槽转矩。

综上所述,大部分学者对高速永磁同步电机优化采用常规的有限元参数分析和田口法[9-10],且仅考虑了部分电机结构参数。本文提出一种基于遗传算法和TOPSIS法的HSPMSM联合仿真优化方法,首先通过ANSYS Maxwell有限元仿真软件对HSPMSM进行参数化建模,更进一步建立4极30槽HSPMSM的Maxwell &Workbench &Optislong联合仿真模型,然后运用遗传算法进行多目标优化得到Pareto解集,使用优劣解距离法(TOPSIS)从解集中选取最优方案,最后对比优化前后高速电机的各项性能,结果表明:采用遗传算法和TOPSIS法对电机进行联合仿真优化,不仅提升了高速电机多目标优化效率,还有效抑制电机转矩脉动和齿槽转矩,改善高速电机电磁性能。

1 HSPMSM参数化建模

高速永磁同步电机初始有限元模型如图1所示,该电机主要是由定子、转子、电枢绕组和永磁体构成,电机各部分初始结构参数如表1所示。

表1 电机初始结构参数

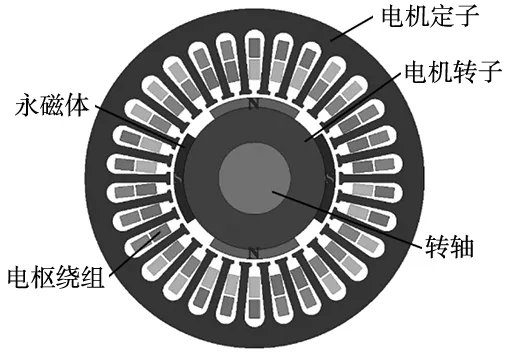
图1 HSPMSM有限元模型

对表1中电机定子、转子和电机气隙等8个主要结构参数进行参数化建模,对应参数化模型如图2所示。

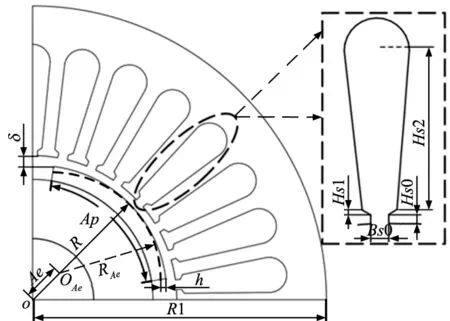
图2 HSPMSM主要结构参数化建模

电机定子外径R1和定子槽内深度Hs2大小会影响定子轭部磁密,影响电机出力;定子槽口和槽肩的尺寸会影响电机齿槽转矩大小,选择合适的尺寸会有效抑制电机齿槽转矩;电机转子极弧系数Ap、磁极偏心Ae和电机气隙的大小会对电机气隙磁密造成影响,也会影响电机转矩脉动和齿槽转矩等性能。因此对电机定子外径R1、定子槽口宽度Bs0、定子槽口深度Hs0、定子槽肩长度Hs1、定子槽内深度Hs2、电机气隙大小δ、磁极偏心距Ae和转子极弧系数Ap参数化建模,根据HSPMSM的实际尺寸规定以上参数变量的范围如表2所示。

表2 电机的优化范围

2 HSPMSM优化变量灵敏度分析

为了有效分析各个变量对电机性能的影响程度,以电机的平均转矩、齿槽转矩和转矩脉动作为优化目标。以ANSYS Workbench为仿真平台,通过Optislong灵敏度分析模块与Maxwell电磁场有限元仿真模块联合,对电机仿真参数化模型进行优化变量的灵敏度分析,优化变量的灵敏度分析直方图如图3所示。

图3 HSPMSM优化变量灵敏度直方图

灵敏度的正负分别表示优化目标随着优化变量的增大而上升和下降,敏感度绝对值较高意味着优化变量对优化目标的影响程度大[11]。由图3可以看出,电机定子外径R1和磁极偏心距Ae对电机平均转矩影响程度大;电机气隙大小δ和磁极偏心距Ae对电机齿槽转矩影响程度大;电机定子外径R1和定子槽内深度Hs2对电机转矩脉动影响程度大。

为了进一步研究灵敏度绝对值较大的变量对于优化目标的影响规律,分别对有限元仿真数据建立二阶多项式数学模型,进行多元二次回归拟合,得到影响程度较大的变量对于平均转矩、转矩脉动和齿槽转矩这3个优化目标的响应面模型。

二阶多项式数学模型如式(1)所示,其中Y为响应值,λ0为常数,λi为一阶系数,λii为二阶系数,λij为二阶相互作用的系数,ε为拟合误差。

(1)

以平均转矩Tavg为优化目标,因为电机定子外径R1和磁极偏心Ae对于平均转矩影响程度较大,因此以电机定子外径R1和磁极偏心距Ae作为优化变量拟合回归方程如式(2)所示,其对应的平均转矩响应面如图4所示。

图4 平均转矩响应面图5 齿槽转矩响应面

Tavg=-219.8+0.9135Ae+3.556R1+
0.01399Ae2-0.00839AeR1-0.0142R12

(2)

从图4可以看出,平均转矩Tavg随着磁极偏心Ae的减小而逐步增大,并且在电机外径R1较大时候增大明显。在磁极偏心Ae较大时,Tavg随着电机外径R1增大呈现先增大后减小的趋势;在磁极偏心Ae较小时,Tavg随着电机外径R1增大呈现增加的趋势。

同理,电机齿槽转矩Tcog关于电机磁极偏心Ae和气隙大小δ影响程度较大,分别以Ae和δ作为优化变量拟合回归方程如式(3)所示,其对应的齿槽转矩响应面如图5所示。

Tcog=-55.44-1.102Ae+1.867δ+
0.007217Ae2+0.01724Aeδ-0.01567δ2

(3)

由图5可知,电机齿槽转矩Tcog随着磁极偏心Ae的增大呈现先急剧减小后略微增大的趋势。在磁极偏心Ae较小时,齿槽转矩Tcog随着电机气隙δ增加而降低;在磁极偏心Ae较大时,电机气隙δ的增加对于齿槽转矩只是略微影响。

同理,电机转矩脉动Trip关于电机外径R1和定子槽深Hs2影响程度较大,分别以R1和Hs2作为优化变量拟合回归方程如式(4)所示,其对应的转矩脉动响应面如图6所示。

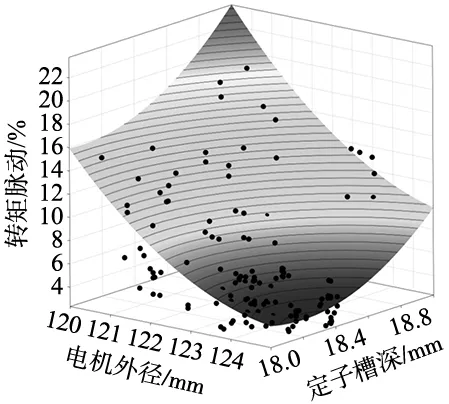
图6 转矩脉动响应面

Trip=7993-86.12R1-282.6Hs2+
0.3741R12-0.4382R1Hs2+9.271Hs22

(4)

由图6可知,转矩脉动Trip随着电机外径R1的增大而减小。在电机外径较小R1时,转矩脉动Trip随着定子槽深的增大呈现先减少后增大的趋势;电机外径R1较大时,转矩脉动Trip随着定子槽深的增大而增大。

因此,在优化HSPMSM电机参数时,由于参数之间复杂的耦合关系,参数的选取会对电机不同性能造成不同的影响,很难从各个参数变化规律中选择出最理想的参数数值,应综合考虑每个参数对电机不同性能的影响,从而确定电机参数的取值。

3 基于遗传算法和TOPSIS法的电机联合仿真优化

对于HSPMSM的优化设计涉及到8个输入变量和3个输出变量,如果采用有限元求解器的多参数优化需要大量运行时间和运算器内存,并且很难考虑全各个电机参数对不同电机性能的影响。

因此将电机Maxwell有限元模型通过Workbench与Optislong进行联合仿真,使用Optislong中集成的智能算法对电机进行优化,联合仿真优化模块介绍如图7所示。为更有效寻找多输入变量和多输出优化目标的全局最优解集,采用具有收敛速度快、计算精度高和需调整参数少优点的遗传算法[12-13],其优化流程如图8所示。

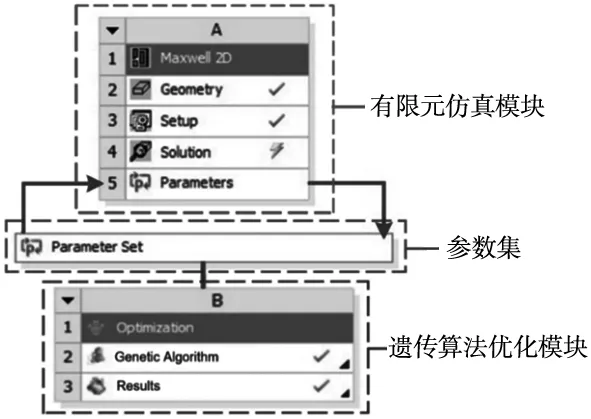
图7 联合仿真优化模块介绍

图8 遗传算法优化流程图

采用遗传算法进行多目标优化,以电机定子外径R1、定子槽口宽度Bs0、定子槽口深度Hs0、定子槽肩长度Hs1、定子槽内深度Hs2、电机气隙大小δ、磁极偏心距Ae和转子极弧系数Ap这8个参数为输入变量,为了确保平均转矩、齿槽转矩和转矩脉动这3个输出变量均得到一定程度优化。将平均转矩最大、齿槽转矩最小和转矩脉动最小作为目标约束,目标函数和约束条件如式(5)所示。

F(x)=[min(Tcog),min(Trip),max(Tavg)]
TcogTavg0

(5)

式中:F(x)为多目标函数,Tcog0、Trip0和Tavg0为齿槽转矩、转矩脉动和平均转矩设置的数值优化下限。

图9为遗传算法多目标优化结果,通常以Pareto 3D最优解集方式呈现,最优解集数据如表3所示。图9中不同坐标轴代表了电机的不同性能。数据点分别表示不同输入变量的粒子,黑色粒子为不符合约束条件的粒子,红色粒子为符合约束条件的粒子,三角形面为Pareto前沿面,Pareto最优解集中优化结果较好的粒子会出现在Pareto前沿面上。

表3 Pareto最优解集

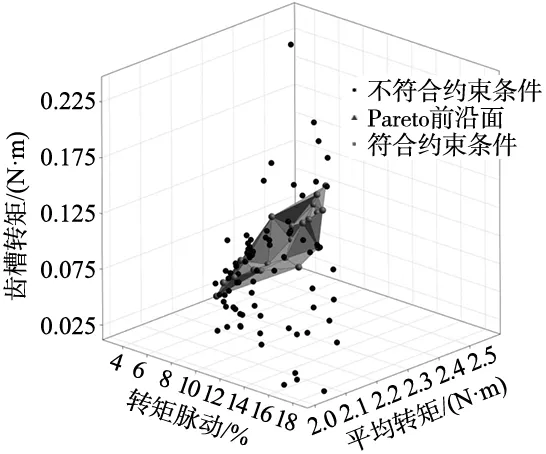
图9 Pareto 3D最优解集

为了从Pareto最优解集中选取全局最优解,使用优劣解距离法(TOPSIS)对Pareto解集进行相对优劣评价,具体算法流程如式(6)～式(10)所示[14-15]。

(1)若有n个数据对象,m个评价指标,如式(6)所示,评价指标以矩阵的形式呈现,初始矩阵为X=[X1,X2,…,Xj]。

Xj=[x1j,x2j,…,xnj]T,(j=1,2,…)

(6)

(3)使用平方和归一化处理数据,每个指标消除量纲之后如式(7)所示。

(7)

(4)求出正负理想向量z+、z-如式(8)所示。

(8)

(5)如式(9)所示,算出正负理想解距离。

(9)

(6)由正负理想解距离算相对接近度Ci如式(10)所示,Ci数值越大表明评价结果越好。

(10)

由以上流程,对表3中最优解集进行TOPSIS优化,不同的电机结构参数为数据对象,评价指标为不同的电机性能,可以得到电机齿槽转矩、转矩脉动和平均转矩的正负理想解如表4所示。

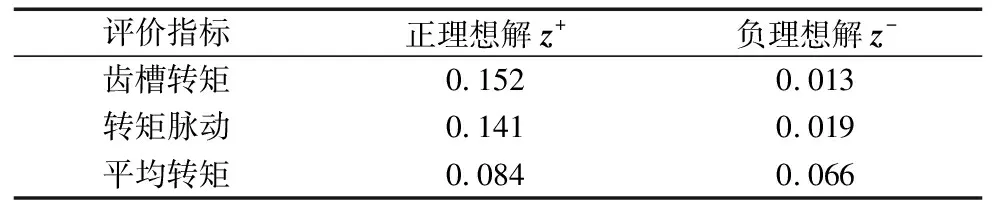
表4 正负理想解

根据正负理想解计算可得正负理想解距离和相对接近度如表5所示,根据排序结果选定第3个解为最优解,确定最合理的电机定子外径R1、定子槽口宽度Bs0、定子槽口深度Hs0、定子槽肩长度Hs1、定子槽内深度Hs2、电机气隙大小δ、磁极偏心距Ae和转子极弧系数Ap这8个电机结构参数。

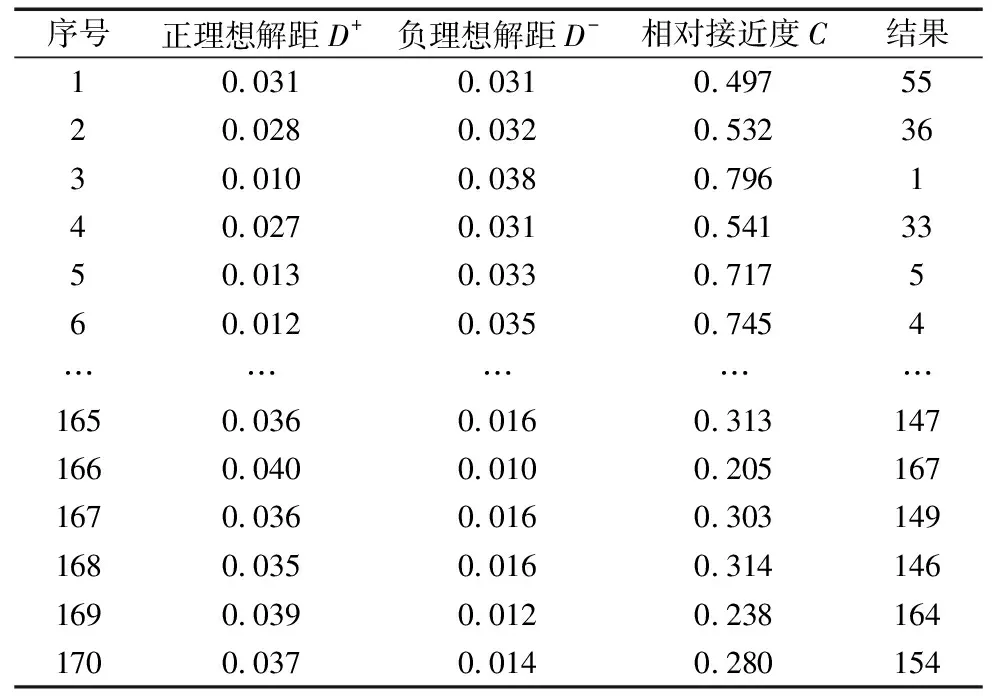
表5 TOPSIS评价计算结果

采用遗传算法和TOPSIS法优化前后电机参数和各个电机性能对比如表6所示,可以看出虽然电机平均转矩略微下降,但电机齿槽转矩和转矩脉动均得到了有效抑制,这对减少电机的振动噪声有所改善。

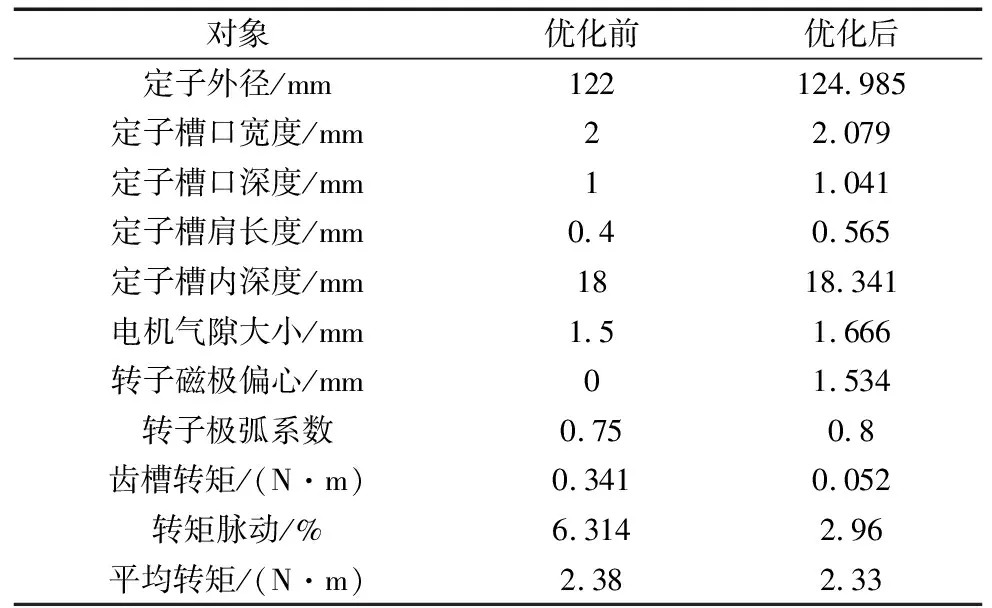
表6 算法优化前后数据对比

4 HSPMSM优化前后性能对比

采用遗传算法和TOPSIS法对HSPMSM的8个电机参数进行多目标联合仿真优化,优化前后电机磁密分布云图如图10和图11所示,可以看出优化后电机的磁密饱和程度较好,磁密最大饱和度由优化前的1.94 T降低至1.79 T,该优化方法有效改善了电机磁场饱和程度。

图10 优化前电机磁密云图 图11 优化后电机磁密云图

由图12～图14可以看出,由于优化后电机采用了磁极偏心,电机优化后气隙磁密基波幅值和反电势幅值仅略微下降,满足电机基本要求,对电机出力影响不大。优化后电机气隙磁密5、7、11次谐波明显降低,有效改善了电机气隙磁密正弦度,对减小电机齿槽转矩和转矩脉动提供有利效果。

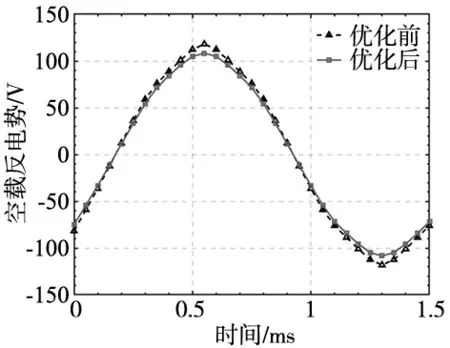
图14 优化前后电机空载反电势对比

由图15和图16可知,采用遗传算法和TOPSIS法对电机进行多目标联合仿真优化前后电机齿槽转矩从0.341 N·m降低至0.052 N·m,降低了85%,电机转矩脉动从6.21%降低至2.96%。电机齿槽转矩和转矩脉动的降低有效改善了HSPMSM振动噪声情况。

图15 优化前后电机齿槽转矩对比 图16 优化前后电机输出转矩对比

因此,本文通过使用遗传算法和TOPSIS法对HSPMSM进行联合仿真优化,不仅减少了电机磁场谐波含量,有效改善了电机气隙磁密正弦度,还削弱了电机齿槽转矩和转矩脉动,提高了电机控制精度。

5 结束语

本文提出一种基于遗传算法和TOPSIS法的HSPMSM联合仿真优化方法,建立4极30槽HSPMSM 的Maxwell &Workbench &Optislong联合仿真模型,运用遗传算法进行多目标优化得到Pareto解集,使用优劣解距离法(TOPSIS)从解集中选取最优方案,总结全文可以得到以下结论:

(1)基于遗传算法的TOPSIS法的HSPMSM联合仿真设计方法,解决了电机多个结构参数输入和多个性能参数输出的多目标优化问题,有效提升电机的优化效率和准确性。

(2)采用遗传算法和TOPSIS法对电机进行多目标联合仿真优化可有效改善电机齿槽转矩和转矩脉动。齿槽转矩从0.341 N·m降低至0.052 N·m,降低了85%,电机转矩脉动从6.21%降低至2.96%。