考虑周向间隙的摆线针轮承载接触分析*

周士冬,韩振华,石万凯,单文桃,刘 昶

(1.江苏理工学院机械工程学院,常州 213001;2.重庆大学机械传动国家重点实验室,重庆 400044;3.成都大学机械工程学院,成都 610106)

0 引言

RV(rotating vector)减速器具有传动比范围大、结构紧凑、传动精度高、运行平稳、噪声低、传动效率高、工作可靠等优点,在工业机器人、高精度机床、自动化设备等领域的发挥着重要作用[1]。摆线针轮齿轮副作为RV减速器中的关键传动部件,其承载传动性能是精密RV减速器设计中的重要环节,因此建立精确的摆线针轮承载接触分析方法显得尤为重要。

摆线针轮承载接触分析主要采用解析法和有限元法,有限元法方面:孙晓超等[2]通过ANSYS建立RV-40E减速器的有限元分析模型,分析了针齿沿摆线轮齿根到齿顶连续动态啮合的接触应力变化规律。张跃明等[3]利用有限元分析软件ANSYS WorkBench,建立摆线轮弹性转角模型,对修形后的摆线针轮进行齿间加载接触分析。SU等[4]利用有限元法建立了摆线针轮的刚柔耦合分析模型。有限元法求解精度高,但计算精确度依赖于模型的网格质量和局部网格的细化程度,庞大的网格数量,将降低模型计算效率,增加求解时间,同时也存在难收敛的问题。

解析法主要是前苏联柯特略者夫提出的轮齿作用力解析力学方法(后简称传统算法)[5],以及在此基础上发展的LTCA(load tooth contact analysis)[6]。何卫东等[7]考虑摆线轮修形引起初始间隙的影响,基于赫兹接触原理,建立了各齿对的啮合力与接触变形的函数关系式,并利用扭矩平衡原理进行迭代求解,计算出啮合齿数、啮合力和接触变形。张东生等[8]在传统受力分析的基础上,通过变形协调原理,提出了一种摆线针轮动态受力分析方法。蒙运红等[9]将实际齿廓公法线上的距离作为啮合间隙,提出了一种修形摆线针轮初始间隙计算方法。LI等[10]考虑修形误差和偏心距误差的影响,基于承载接触分析模型,提出了一种计算啮合刚度的新方法。LIN等[11]提出了一种基于摆线齿廓离散化的摆线针轮轮齿接触分析方法。杨婧钊等[12]考虑摆线针轮传动过程中节点位置的变化对啮合间隙的影响,基于轮齿接触分析,提出一种新的啮合间隙计算方法。HUANG等[13]考虑接触齿面的摩擦以及摆线轮的支撑轴承刚度,提出了一种基于影响系数法的摆线针轮承载接触分析方法。传统算法常采用初始法向间隙作为啮合间隙,只能计算初始位置的啮合间隙,而LTCA的共轭方程的求解对初值非常敏感,且忽视了摆线轮随输入轴公转消隙的过程,同时,其承载力学模型依旧基于法向间隙作为啮合间隙,未考虑摆线针轮的承载变形下的自转形式,使得啮合间隙计算结果与实际有所误差。

鉴于此,本文从啮合间隙入手,考虑摆线轮先公转啮合,后承载变形的初始运动形式,提出摆线轮自转方向上的最短弧长作为周向间隙,基于转化机构法和坐标变换原理,建立周向间隙几何模型,运用变形协调条件、赫兹接触理论及扭矩平衡方程建立摆线针轮承载接触分析模型。

1 传统初始法向间隙计算方法

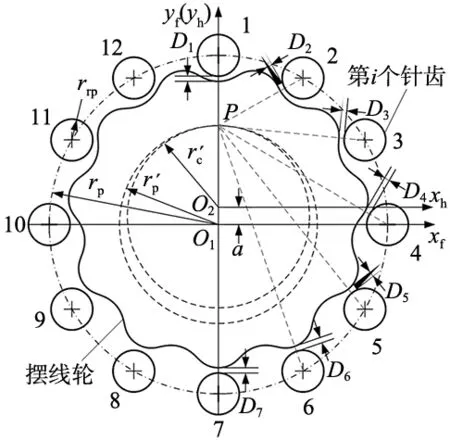
图1 初始法向间隙分布图

(1)

式中:φi是第i个针齿相对于转臂O1O2的转角,K1为短幅系数,Δrp为移距修形量,Δrrp为等距修形量。

然而,该方法存在以下不足之处:

(1)初始法向间隙式是基于一定假设条件推导出来的,与实际有一定的误差。根据初始法向间隙式(1)可知,Di=0时可求出φ0=arccosK1,即在此φ0处有一个针齿和摆线轮接触,其它各齿对的初始法向间隙是在此条件下计算出的。实际中,针齿是等相位分布在针轮分布圆上,在φ0处未必存在针齿与摆线轮接触,这将导致各齿对之间的初始法向间隙与实际差别。

(2)初始法向间隙式是针对摆线轮和针轮初始位置处,随着摆线针轮行星传动,无法求得任意输入转角下各齿对的初始法向间隙,只能求初始位置下的初始法向间隙,无法准确计算空载和承载传动误差,通用性不强。

2 周向间隙计算方法

2.1 周向间隙的计算原理

针对初始法向间隙计算方法存在的问题,从啮合间隙入手,考虑摆线轮先公转啮合,后承载变形的初始运动形式,提出了一种以周向间隙作为啮合间隙的摆线针轮承载接触分析计算方法,具体原理为:

图2 摆线轮与针轮由初始位置到接触示意图

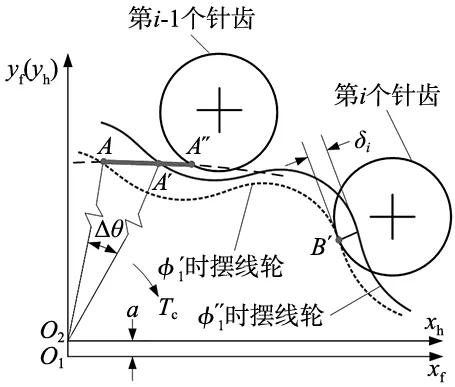
图3 摆线轮与针轮由接触到变形示意图

2.2 周向间隙几何建模

图4 摆线针轮行星传动坐标系统

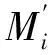
(2)

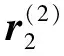
(3)

式中:Km为修形后的短幅系数,Km=aZp/(rp+Δrp)。

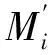
(4)

(5)

(6)

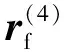
(7)

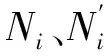
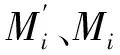
(8)

(9)

2.3 周向间隙模型求解

具体周向间隙模型求解如下:

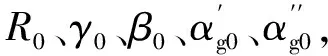
(10)

步骤3:为计算φ1时最先接触齿对转过的角度,使i=1,…,Zp/2,重复上述步骤1和步骤2求得各齿对周向公转角θi,通过比较各齿对周向公转角θi大小得到最小周向公转角θmin,可表示为:

θmin=min(θi)

(11)

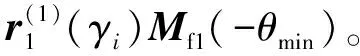
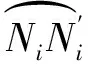
(12)

(13)

2.4 摆线针轮实际力臂的计算

图5 各齿对力臂示意图

(14)

3 摆线针轮承载接触分析

根据上述方法提出摆线针轮周向间隙与实际力臂计算方法,建立变形协调与扭矩平衡条件,即可建立修形摆线针轮承载接触分析模型。

3.1 摆线针轮啮合齿数判定与变形协调条件

如图6所示,在空载状态下,当摆线轮转过最小周向公转角θmin,一针齿与摆线轮刚好接触,其它各齿对之间存在大小不等的间隙角θci。由于阻力矩Tc的作用,各齿对产生接触变形δi,使得摆线轮产生扭转变形角Δθ,当扭转变形角Δθ大于各齿对的间隙角θci时,该齿对参与啮合,否则不参与啮合。第i个齿对的接触变形δi与力臂li呈定比例关系(变形协调条件),其关系式为:

图6 间隙与扭转变形角示意图

(15)

3.2 啮合力与接触应力计算方法

根据赫兹接触理论[15],摆线轮和针齿的接触可以假设为两个平行圆柱体的接触,其接触变形wi可表示为:

(16)

式中:Fi为第i个齿对之间的啮合力,ρ为摆线轮曲率半径,L为摆线轮齿宽,E1、E2分别为摆线轮和针轮的弹性模量,μ1、μ2分别为摆线轮和针轮的泊松比,b为接触半宽,具体可表示为:

(17)

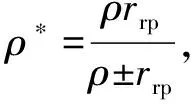
由式(16)可知,啮合力Fi和接触变形wi呈现非线性关系,在材料属性相同的情况下,其接触刚度(kni=Fi/wi)大小随着载荷和接触点曲率的变化而变化。虽然由方程可以得到接触力Fi和接触变形wi的关系式wi=f(Fi),但是无法通过简明数学表达式写出Fi=f-1(wi),利用曲线拟合的方法,在某一力区间离散,继而求解出离散力对应的接触变形,再用Fi=CiwiPi来逼近wi=f(Fi),利用MATLAB多项式拟合函数求解出Ci、Pi。

Fi=CiwiPi=Ci[(Δθ-θci)li]Pi

(18)

设摆线轮在负载扭矩Tc的作用下,最先接触齿为第m1齿对,最后进入啮合的为第m2齿对,则有(m2-m1+1)个齿对共同啮合传力,根据扭矩平衡方程,可得:

(19)

通过变形协调条件式和扭矩平衡方程式,建立摆线针轮副的力学分析模型,该模型的计算流程图如图7所示:

图7 摆线针轮受力分析流程图

步骤1:给定摆线针轮齿轮副的设计参数,由式(13)得到的间隙角θci和本节计算的拟合系数Ci、Pi;初始值Δθ1为摆线轮只与一个针齿啮合产生的扭转变形角,初始值Δθ2为摆线轮与半数针齿啮合产生的扭转变形角,则修形摆线轮产生的扭转变形角Δθ介于(Δθ1～Δθ2)之间,为提高迭代效率,采用黄金分割法初选扭转变形角Δθ;当扭转变形角Δθ大于间隙角θci为传力齿,否则为非传力齿;

通过该流程中的步骤1即可计算摆线针轮副啮合齿数,而通过整个计算流程可求得啮合力Fi,利用赫兹接触公式,即可得到对应接触应力σH大小,其接触应力表达式为:

(20)

3.3 传动误差计算方法

传动误差是指输入轴转动任意角度时,输出轴理论转角和实际转角的角度误差。在空载情况下,由于负载扭转很小,可忽略不计,其传动误差主要来源于摆线轮和针轮之间的间隙,最小周向公转角θmin反映空载传动误差的大小,当φ1从0变化到2π,利用2.2节式(11)求得到一个周期下的最小周向公转角θmin,此时空载传动误差(TE)为:

2018年4月6日晚发生低温冻害，陕西淳化果区-7.2℃极端低温持续长达4小时，冻害过后低温又持续了3天之久，致使果区坐果率降低，一般果园减产20%，有的超过40%，个别绝收。幼果期低温给果锈普遍发生创造了条件，使得2018果季苹果商品率大幅下降。

TE=0-θmin/iH

(21)

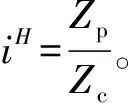
在承载情况下,由于负载扭矩Tc作用,摆线轮和针轮的接触使得摆线轮产生一个扭转变形转角Δθ,因最小周向公转角θmin和扭转变形角Δθ的存在,使得输出轴会产生滞后,输入与输出的瞬时传动比将不在是一个定值,从而引起承载传动误差。当输入轴φ1从0变化到2π,由式(11)和式(15)得到一个周期下的最小周向公转角θmin和扭转变形角Δθ,此时承载传动误差(LTE)为:

LTE=0-(Δθ+θmin)/iH

(22)

4 实例计算与结果分析

4.1 对比分析

基于上述方法,以摆线针轮副参数为例(如表1所示),利用本文提出的摆线针轮承载接触分析方法计算啮合力和接触应力,并与传统算法和LTCA进行对比评价。

表1 摆线针轮齿轮副设计参数

图8为本文算法、传统算法和LTCA啮合间隙对比图,从图8中可以看出,本文算法的周向间隙与传统算法和LTCA的法向间隙的整体变化趋势相近,都是先减小后增大,但在数值上有一定的差异,3种算法的啮合间隙都在第5齿达到最小值,其最小值分别为0 mm和3.02×10-9mm,2.28×10-5mm,同时,本文算法与传统算法和LTCA相比都在第5齿处的差值最小,在第5齿的两侧差值逐渐增大,同时,在第3齿本文算法与传统算法相对误差最小为13.2%,在第4齿本文算法与LTCA相对误差最小为0.8%,都在第19齿相对误差最大,其分别为739.3%、655.4%。

图9为本文算法的实际力臂与传统力臂对比图,从图9中可以看出,实际力臂与传统力臂的整体变化趋势相近,都是先增大后减小,但在数值上有一定的差异。在针齿1位置的传统力臂为0 mm,而本文算法的实际力臂为26.1 mm,这是由于未修形下的摆线轮与针齿1的啮合点在转臂O1O2的延长线上,进而力臂为0 mm,而传统力臂以此啮合点来计算修形摆线轮与针齿1的力臂,与实际不符,使得实际力臂与传统力臂在针齿1的相对误差最大为100%,在第8齿相对误差最小,其值为0.02%,随后逐渐增大。但实际力臂与传统力臂最大值对应的齿号不同,二者力臂最大值分别为第5齿和第6齿,其相对误差为0.16%。

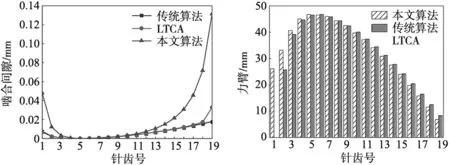
图8 啮合间隙对比图 图9 实际力臂与传统力臂对比图

图10和图11分别为本文算法、传统算法和LTCA的啮合力和接触应力对比图,从图10和图11可以看出,本文算法相较于传统算法和LTCA的啮合力和接触应力的整体变化趋势相近,都是先增大后减小,但数值不同,3种算法都是从第3齿承载受力进入啮合,在第11齿受力变为0,退出啮合,啮合齿数都为8齿,但本文算法和LTCA都在第5齿啮合力最大,而传统算法在第6齿啮合力最大,3种算法的啮合力最大值分别为910.7 N、899.9 N、935.6 N,本文算法最大啮合力分别相对于传统算法和LTCA增大2.7%、3.7%,同时3种算法的接触应力都在第7齿达到最大值,且最大接触应力分别为1 443.4 MPa、1 454.5 MPa、1 490.1 MPa,本文算法最大接触应力分别相对于传统算法和LTCA增大3.2%、2.4%。

图10 啮合力对比图 图11 接触应力对比图

综上所述,通过对比可以看出,本文算法的啮合力与接触应力相较于传统算法和LTCA整体变化趋势相近,但数值上有一定的差距,其原因为:①本文算法考虑摆线轮的先公转啮合,后承载变形的初始运动形式,采用更合理的周向间隙;②本文算法求得实际啮合点位置,进而得到实际力臂大小;③实际中摆线轮齿廓曲率不是一个定值,导致接触刚度呈现非线性,而本文算法采用更合理的非线接触刚度建立模型。

4.2 承载接触分析

以表1中的参数为例,利用本文提出的摆线针轮传动承载接触分析模型,求得在不同输入转角下的啮合力、接触应力、啮合齿数以及传动误差的变化,图12和图13分别为不同输入转角下针齿1的啮合力、接触应力变化曲线和曲率半径变化曲线,从图12和图13可以看出,针齿1在输入转角为0.30 rad时开始参与啮合,在输入转角为1.56 rad时结束啮合,啮合力和接触应力都先增大后减小,然后再增大,之后再减小。在此变化趋势下啮合力和接触应力都产生两个极大值和一个极小值,啮合力的在输入转角为0.55 rad时取得第一个极大值亦是最大值为965.2 N,在输入转角为0.87 rad时啮合力取得第二个极大值为935.2 N,而接触应力在输入转角为0.69 rad时取得第一个极大值为1 012.5 MPa,第二个极大值在输入转角为1.04 rad时取得亦是最大值为1 523.6 MPa,同时在输入转角为0.71 rad时啮合力和接触应力同时取得极小值,分别为608.9 N、908.9 MPa。通过与图12对比可以看出,啮合力和接触应力的极小值点,恰好为摆线轮齿廓由凸到凹过渡的位置,使得曲率半径产生突变,对啮合力影响较大,而对接触应力影响较小。对比图10、图11,可以看出全周期下的最大啮合力与最大接触应力比初始位置分别增大29.6 N和33.5 MPa。

图12 针齿1的啮合力和接触应力随输入转角的变化 图13 针齿1的曲率半径随输入转角的变化

如图14、图15分别为输入转角从0到2π变化时的空载传动误差和承载传动误差,从图中可以看出,随着输入转角的增大空载传动误差从-2.823′′到-2.818′′再到-2.823′′呈现周期性的变化,其平均值为-2.821′′,而承载传动误差从起始点-3.186′′到-3.201′′,其中产生两个峰值,第一个峰值为-3.186′′,第二个峰值为-3.189′′到呈现周期性的变化,其平均值为-3.191′′。图16为在不同输入转角下啮合齿数的变化曲线图,随着输入转角的增大啮合齿数由8齿变为7之后再变为8齿,呈现周期性变化,其周期都为相邻针齿夹角2π/Zp。

图14 不同输入转角下的空载传动误差变化趋势 图15 不同输入转角下的承载传动误差变化趋势

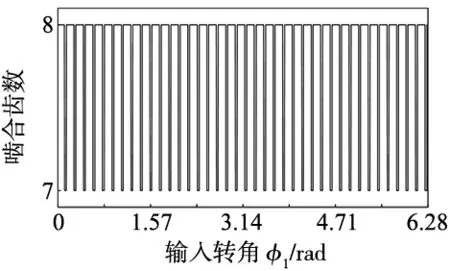
图16 摆线针轮啮合齿数随输入转角的变化

综上所述,随着输入转角的变化啮合力与接触应力在变化趋势相近,都在同一位置产生突变,啮合力突变幅度较为明显,而接触应力突变幅度相对平缓;同时,啮合齿数、空载传动误差、承载传动误差都呈现周期性变化,其周期都为相邻针齿夹角2π/Zp,但空载传动误差、承载传动误差变化趋势不同,空载传动误差在一个变化周期内只有一个峰值,承载传动误有两峰值,其最大值和最小值所在的位置也不同;在一个2π/Zp周期内,啮合齿数大多数为8齿传力,7齿传力占少数。

5 结论

本文考虑摆线轮实际运动形式,建立周向间隙下的摆线针轮承载接触分析模型,分析摆线针轮行星承载传动下的啮合齿数、啮合力、接触应力和传动误差等承载传动性能,主要结论如下:

(1)与传统算法和LTCA对比,啮合力与接触应力整体变化趋势相近,啮合齿数相同,但数值上有着一定的差异,其计算出的最大啮合力分别增大2.7%、3.7%,最大接触应力分别增大3.2%、2.4%。

(2)随着输入转角的增大,啮合齿数、空载传动误差、承载传动误差,不是恒定值而是呈现周期性变化,其周期为相邻针齿夹角2π/Zp。

(3)全周期下的啮合力和接触应力存在突变,突变位置恰好为摆线轮齿廓曲线凹凸过渡点。同时,全周期下的最大啮合力和最大接触应力大于初始位置,因此,采用全周期下的最大啮合力和最大接触应力更加合理。