C、Mn对γ-Fe层错能影响的第一性原理研究

2023-11-28蒋人豪卢冠杰

上海金属 2023年6期

蒋人豪卢冠杰董瀚史文王洋

（1.上海大学材料科学与工程学院，上海 200444；2.上海大学计算机工程与科学学院，上海 200444）

先进高强钢因具有良好的力学性能而被广泛应用于众多领域［1-3］。其优异的力学性能主要来源于变形过程中奥氏体发生的相变诱导塑性（transformation induced plasticity，TRIP）和／或孪晶诱导塑性（twinning induced plasticity，TWIP）效应［4］。这两种变形机制都是提高材料强韧性的重要手段，不同之处在于TRIP效应是钢在变形过程中亚稳奥氏体经历γ →ε →α′相变或γ →ε 相变［4］，使材料的强度和塑性得到提高，而TWIP效应则是在变形过程中出现孪晶组织，使材料的强韧性得到改善［5］。层错能（stacking fault energy，SFE）是决定材料变形机制的重要因素之一［6］。层错能小于18 mJ／m2，相变是主要的变形机制；层错能介于12 ～35 mJ／m2之间，孪晶是主要的变形机制；层错能大于35 mJ／m2，滑移占主导［7-10］。层错能是一种原子尺度的性能［8］，试验中任何一个细微的变化都将影响层错能的准确度，而采用理论计算可准确获得各元素对层错能的影响。C、Mn是先进高强钢中的重要元素［11-12］，对层错能具有重要影响，故本文通过第一性原理计算研究了C、Mn 对γ-Fe 层错能的影响，并以形成层错后的自由能ESF为依据确定C、Mn 在γ-Fe 中的最稳定位点，计算和预测了相应的层错能和变形机制。

1 理论方法

层错是金属中常见的晶体缺陷，由正常堆垛的原子层出现错排而引起。在面心立方（face center cubic，FCC）金属的密排面上，原子的正常堆垛顺序从... ABCABCABC... 转变为...ABCABC ｜BCABC...时，就形成了一个内廪层错，层错区域变为HCP（hexagonal close packed）结构。“｜”代表层错所在位置。γSF表示层错能，表达式为，其含义为自由能之差与层错面积之比。Gdef、Gfcc、A分别代表形成缺陷时的自由能、完美排列晶体的自由能以及层错面积。本文采用Bleskov等［13］提出的层错模型，由FCC 晶胞经过切面得到，如图1 所示。层错模型有12层，每层2 个原子。图1 中红色虚线为层错面，层错面上半部分方向进行剪切。位移量为时，会形成一个势垒USF（unstable stacking fault），对应的层错能为γUSF，γUSF越大，变形需要克服的势垒越大。位移量为时，在层错面附近形成ε 相（intrinsic stacking fault，ISF结构），如图1（e）绿框所示。ISF 结构对应的层错能为内廪层错能（intrinsic stacking fault energy，ISFE），即γISF。γISF＞0，代表形成缺陷时体系自由能高于FCC 晶体，FCC 相更稳定，不会发生γ→ε转变；γISF＜0，容易发生γ→ε转变。在形成ISF 结构后，将图1（e）蓝框内的原子进行“二次剪切”，可获得孪晶（twin stacking fault，TSF结构），剪切时存在两个特殊值，分别为γUTF孪晶势垒与γTSF孪晶缺陷能［14］。

图1 构建层错模型示意图（（a）FCC晶胞；（b）切面后晶胞的侧视图；（c）切面后晶胞的俯视图；（d）扩胞后的层错模型，黄色原子磁序为正，紫色原子磁序为负；（e）ISF结构，蓝框内为ε相；（f）TSF结构，黄框内为孪晶）Fig.1 Schematic diagrams of building a stacking fault model（（a）FCC unit cell；（b）side view of the unit cell after sectioning；（c）top view of the unit cell after sectioning；（d）stacking fault model obtained by cell expansion，where yellow atoms represent positive magnetic order，and purple atoms represent negative magnetic order；（e）ISF structure，ε phase in the blue box；（f）TSF structure，twinning in the yellow box）

本文通过Jo 等［15］的塑性理论，由γd值判断层错、孪晶、滑移倾向，表达式为

式中：－0.5 ＜γd＜0 时，层错与滑移共存，但层错占主导；0 ＜γd＜2 时，孪晶与滑移共存，且γd越小，孪晶的比例越高；γd＞2 时，仅存在滑移。

此外，理想状态下FCC 金属的孪晶形成能力可通过固有孪晶判据P来判断［16］，P越大说明孪晶能力越强，表达式为：

孪晶形成的另一个重要因素是临界孪晶应力。临界孪晶应力τcrit的值越小，说明孪晶越易形成。Kibey等［17］提出了FCC 金属临界孪生应力的表达式，如下：

所有计算通过Vienna Ab-initio Simulation Package（VASP）软件包实现［18-19］。离子-电子间的相互作用采用缀加投影波赝势方法来描述（projected augmented wave，PAW），交换关联效应通过广义梯度近似框架（generalized gradient approximation，GGA）下的PW91 进行处理［20］。经过收敛性测试后确定平面波截断能为450 eV。布里渊区的积分采用Monkhorst-Pack特殊k点网格方法，经过收敛性测试后确定k 点为7 ×15 ×1。计算时的收敛标准为10－4eV。

2 结果与讨论

2.1 γ-Fe的层错能

主要对无磁（non-magnetic，NM）和反铁磁（antiferromagnetic，AFM）态γ-Fe 的层错能进行计算。γ-Fe面心立方模型经弛豫后得到NM态的晶格常数为3.45 Å，而AFM态的为a ＝b ＝3.41 Å，c／a ＝1.07，与文献中的弛豫结果一致［21］。弛豫后的晶胞经切面得到层错模型，其广义层错能（generalized stacking fault energy，GSFE）如图2 所示。由图2 可知，随着剪切运动的位移量增大，NM与AFM态γ-Fe的GSFE均呈现出先上升后下降的趋势，前半段的上升表明势垒的形成，随后的下降表明开始形成内廪层错。层错能的计算结果如表1 所示。NM 态γ-Fe 的γUSF与γISF分别为478、－400 mJ／m2，与Medvedeva 等［22］的结果比较接近，而AFM态γ-Fe的γUSF与γISF分别为239、122 mJ／m2，与Cui 等［23］的计算结果较为接近。这说明本文设置的计算参数具有相当的可靠性。从自由能的角度考虑，NM态γ-Fe 发生剪切运动后倾向于形成具有HCP 结构的ε 相。但引入磁性后，层错能由负转为正，ε 相不容易产生。实际奥氏体为顺磁性，净磁矩为0，而反铁磁性的净磁矩也为0，故采用反铁磁的计算结果更接近实际。同样后续计算的磁性也设置为反铁磁。

图2 NM（a）与AFM态（b）γ-Fe的广义层错能曲线Fig.2 Generalized stacking fault energy curves of γ-Fe in NM and AFM states

2.2 C、Mn对γ-Fe层错能的影响

C是间隙原子，位于层错模型的八面体间隙位置；Mn 是置换性原子，通过替换层错模型中的Fe进入模型。将合金原子与层错面的距离定义为n（n ＝0，1，2，3），其中n ＝0 表示合金原子位于层错面上，n ＝1，2，3 则表示该合金原子位于层错面下方且距离层错面1，2，3 个原子层处。具体原子位置示意图如图3 所示。

表2 为Fe24C1 模型中C 与层错面之间的距离不同时计算得到的γUSF和γISF，图4 为4 个不同C位点的GSFE曲线。由图4 可知，n ＝0 位点的GSFE曲线变化趋势与其他3 个位点的趋势不同。n ＝0 位点的C正好位于层错面上，当位移量达到时，层错面上方的Fe正好处在C的正上方，在层错区域形成了一种不稳定结构，在图中则表现为该位移量下的层错能达到了最大值。当位移量为时，层错能达到了局部极小值。此外，C 在n ＝1，2，3 处的GSFE 曲线变化趋势与γ-Fe 的一致，分别在位移量为和时达到局部最大值与局部最小值，即γUSF和γISF。当C 远离层错面时，γUSF与γISF均逐步下降，都在n ＝3时降至最低。同时，n ＝3 位点处自由能最低，C 此时应处于最稳定状态，故Fe24C1 模型的C取n ＝3 位点。文献［24］提到，层错运动会将C挤出层错区域，而在本文计算模型中，n ＝3 处的C 处于层错区域外，因此C位于n ＝3处时的γISF应为C对γ-Fe的γISF真实影响。与γ-Fe 相比，C 使γISF提高约20 mJ／m2，γUSF提高约38 mJ／m2。

表2 Fe24C1 模型中C、Mn在不同位点对应的γUSF与γISFTable 2 γUSF and γISF corresponding C and Mn at different sites in Fe24C1 model

图4 C处于不同位点时的广义层错能曲线Fig.4 Generalized stacking fault energy curves of C at different sites

表2 还列出了Mn与层错面之间的距离不同时的γUSF和γISF。Mn位于n ＝0 位点时γISF最低，为52 mJ／m2，相比于γ-Fe，γISF约降低70 mJ／m2。当Mn远离层错面时，对γISF的影响逐渐减弱直至趋近于γ-Fe。此外，当Mn 远离层错面时，γUSF呈下降趋势，说明随着Mn的远离，发生变形的势垒降低。从自由能的角度考虑，Mn在n ＝0 位点处，ESF最低，故Mn在此位点时最稳定。

确定C、Mn 在层错模型中最稳定的位点后，按图1 所示进行“二次剪切”，计算γUTF与γTSF，结果如表3 所示。由表3 知，γ-Fe的γUTF为420 mJ／m2，加入C 后γUTF提高，为443 mJ／m2，说明形成孪晶的势垒上升；加入Mn 后γUTF大幅度下降，为174 mJ／m2，说明形成孪晶的势垒下降。

表3 C、Mn在γ-Fe中最稳定位点对应的γUSF、γISF、γUTF、γTSFTable 3 γUSF，γISF，γUTF，γTSF of C，Mn at the most stable sites in γ-FemJ／m2

2.3 变形机制预测

依据表3 的层错能计算孪晶判据，结果如表4 所示。γ-Fe的γISF远高于0，层错难以形成。按照γd理论，γ-Fe 的γd值介于0 ～2 之间，表明变形时兼具孪晶与滑移，而PTwinning的值为8.92，表明γ-Fe变形时具有较弱的孪晶形成能力。综上，γ-Fe变形机制应以滑移为主，兼具少量孪晶。

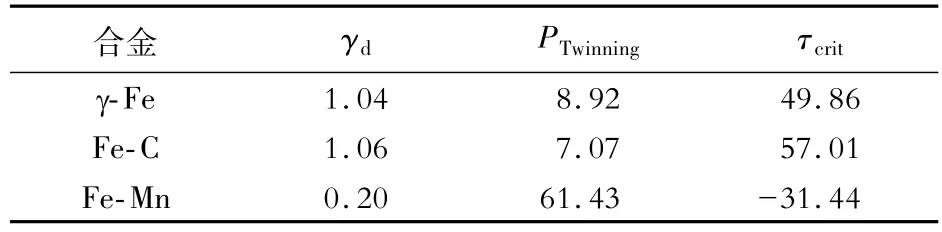
表4 孪晶判据计算结果Table 4 Calculated twinning criteria

加入C后，γISF上升，滑移更容易形成。另一方面，C导致γd上升，相比于γ-Fe，滑移的比例增加。同时，γUTF比γ-Fe 的高，使PTwinning下降、临界孪晶应力τcrit上升，因而加入C 后孪晶形成能力比γ-Fe更弱，Fe-C的变形机制以滑移为主。

Fe23Mn1 模型中，Mn 的加入使γISF显著下降，但仍远大于0，故层错难以形成。相较于γ-Fe，Fe23Mn1 的γd大幅度下降，PTwinning大幅度上升，因此Mn在一定程度上有利于形成孪晶。同时，加Mn后临界孪晶应力τcrit大幅度降低，说明Mn的存在可能比γ-Fe 更容易形成孪晶。综上，Fe-Mn变形时以滑移为主，孪晶为辅。