螺旋运动系数对弧齿锥齿轮齿形的影响规律*
2023-11-28段志宏王志永
段志宏,王志永,张 竹,张 宇
(中南林业科技大学机电工程学院,长沙 410004)
0 引言
弧齿锥齿轮是现代机械传动领域中的关键零件,在弧齿锥齿轮制造过程中因机床误差、热变形等不可控因素,会使得实际齿面与理论齿面之间产生偏差,即齿面误差,传统上采用比例修正的方法来调整齿面的形状,以消除齿面误差的影响。随着精密测量技术的发展,利用齿轮测量中心或者三坐标测量机对齿面进行测量,获取齿面的齿面误差,通过修正机床调整参数和刀具参数等实现对弧齿锥齿轮齿面几何精度的控制成为了当前齿面误差修正技术的主流。
针对齿面形状控制的研究,李丽霞[1]研究了机床调整误差对弧齿锥齿轮齿面几何精度的影响;曹康[2]对螺旋锥齿轮精确几何建模与齿面误差反调修正进行了研究;王志永等[3]针对机床误差对螺旋锥齿轮齿形的影响规律进行了研究,并通过实验验证了分析结果的正确性;唐进元等[4]就机床调整参数误差对小轮齿面误差影响的规律进行了理论研究;聂少武等[5]借助二阶曲面对齿面偏差拓扑的近似表达,将齿面拓扑修形分解成5个方向,并建立了对应的修正数学模型,反求出了修形齿面的小轮加工参数;张宇等[6]研究了螺旋运动及刀具参数对双重螺旋法加工齿面特征的影响规律;吴聪等[7]研究了机床调整参数误差对双重螺旋法加工的螺旋锥齿轮小轮齿面误差的影响规律;耿龙龙等[8]基于弧齿锥齿轮双重螺旋法加工数学模型,分析了各项加工参数误差对齿面拓扑结构的影响程度。
目前,国内主流数控弧齿锥齿轮加工机床普遍具备高阶运动的功能,包括滚比修正、螺旋运动修正、垂直运动修正等。但在实际切齿加工计算时只计算出基本调整参数和一阶螺旋运动系数,并未用到其他高阶运动系数,未能发挥数控机床的万能运动特性。且在实际加工弧齿锥齿轮过程中,操作人员在调整齿轮副的接触区时,并不清楚机床调整参数中的高阶运动系数对齿面拓扑形状的影响规律,因此无法充分运用高阶运动系数来实现对齿面形状的调整。现有文献中均未对一至六阶螺旋运动系数对弧齿锥齿轮齿面形状的影响进行研究。
论文针对国内加工现状,探究一至六阶螺旋运动系数对弧齿锥齿轮齿面形状的影响规律,进一步为弧齿锥齿轮实际加工过程中的齿面调整提供理论依据,合理利用机床的万能运动特性。
1 齿面数学建模
弧齿锥齿轮的齿面几何形状是由刀具和齿坯在实际加工中的复杂相对运动和相对位置决定的。以左旋齿轮为例,左旋齿轮在机床调整位置时的情况如图1所示。在坐标系σ={O;i;j;k}中,O是机床的中心,i、j、k分别为坐标轴正方向的单位矢量,i-j平面是机床平面,k的正方向指向摇台体内,Oc为刀尖平面与刀盘轴线的交点,O1为设计时的交叉点,b为刀盘轴线在机床平面内的投影,c为刀盘轴线的单位矢量,Em为垂直轮位,S为径向刀位,q为角向刀位,矢量p为工件的轴线,XB为床位,Xp为水平轮位修正量,δm为轮坯安装角。
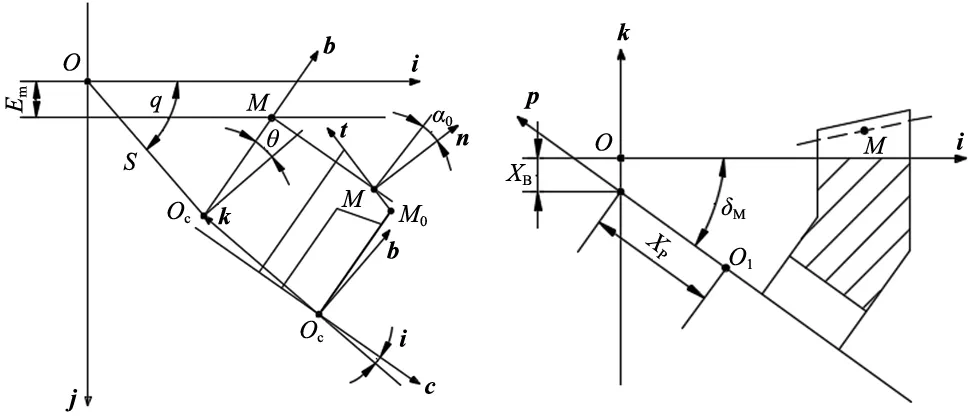
图1 左旋齿轮加工坐标系
在文献[9]中,采用矢量运算的方式,建立了刀盘圆锥切削面上任意一点M的法矢n、M点沿圆锥母线方向的单位矢量t、M点以机床中心O为原点的矢量方程r和M点以齿轮的设计交叉点O1为原点的矢量方程rc。由矢量方程r所确定的刀具切削面是以摇台角q和刀盘的相位角θ为参变量的复杂运动曲面,被加工齿面与刀盘的切削面是共轭曲面,根据产形轮与齿轮之间的相对运动关系,引入一至六阶螺旋运动系数,此时工件的床位为:
(1)
工件沿产形轮轴线方向的速度为:
(2)
式中:XB0为齿轮处于调整位置时的床位,H1、H2、…、H6为一到六阶螺旋运动系数。
由啮合方程可以求得齿面上的点与M点共轭接触时的q、θ以及工件的转角φ。从而求得工件在调整位置时齿面上的点以O1为原点的径矢rw及其法矢nw:
rw=(prc)p+cosφ(p×rc)×p+sinφ(p×rc)
(3)
nw=(pn)p+cosφ(p×n)×p+sinφ(p×n)
(4)
2 齿面离散点参数的计算
计算理论齿面离散点空间坐标及其法矢[10]是进行齿面误差测量和齿面形状分析的前提条件,同时也是实现弧齿锥齿轮数字化制造的关键环节之一。弧齿锥齿轮的齿面属于复杂的空间曲面,其齿面精度和齿面误差的测量更为困难,通常采用对齿面进行离散化处理的方法,即在弧齿锥齿轮理论齿面的旋转投影面上规划一定的测量网格,对齿面进行逐点测量。为了完整全面的反映齿面的形状特征,所有的网格点都应与实际齿面上的点一一对应,通常在齿高方向取5行,在齿长方向取9列,共计45个离散点。
根据AGMA标准[11],划分网格点时要对整个齿面进行一定的收缩,以避开齿根和齿顶以及轮齿大小端的圆角和倒角。通常在轮齿两侧大小端各收缩齿宽的10%,在齿根和齿顶位置,两端各收缩全齿高的5%且不能少于0.6 mm。设定收缩量之后再根据网格点数将收缩之后的齿面沿各边界等距划分,如图2所示。
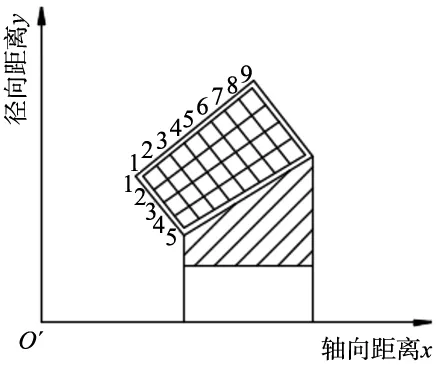
图2 轴截面上的齿面离散点
此后再根据齿坯参数以及收缩后的齿面网格,就可以计算出各离散点在以交叉点O1为原点的坐标系中的坐标值(x(i,j),y(i,j)),其中i=1~9,j=1~5。
如图2所示,设齿面上的M点沿齿轮轴线到O1的距离为x,到齿轮轴线p的距离为y,则有:
y=|rw×p|
(5)
x=-rw·p
(6)
式中:x、y是q和θ的函数,给定了q和θ的值,再根据式(5)和式(6)就能求得x、y的值。如果给定了齿面上离散点的坐标值,就可以利用二元迭代的方法求解其对应的q和θ,随后再利用式(3)、式(4)进而求得理论齿面上对应每一个离散点的径矢rw和法矢nw,此后再经过一次坐标变化,即可将其转换到测量坐标系中,利用三坐标测量机或者齿轮测量中心就可以根据齿面离散点的空间坐标和法矢进行实际齿面的齿面误差的测量。
3 齿形改变量的计算
齿轮测量中心在测量弧齿锥齿轮时,测量路径的规划通常以齿面的中心为参考点,然后沿理论齿面的法矢方向接近测量点,以“S”形的路径分别对大端和小端进行测量。再通过软件的处理,就可以得到齿面上各个离散点对应的齿面误差,绘制出实际齿面相对于理论齿面的齿面误差改变拓扑图。
以工厂实际生产的某弧齿锥齿轮小轮为例(采用双重螺旋法加工),分析各阶螺旋运动系数对齿面形状的影响规律。齿轮副的基本参数如表1所示,加工齿轮的机床调整参数和刀具参数如表2所示。

表1 齿轮副的基本参数
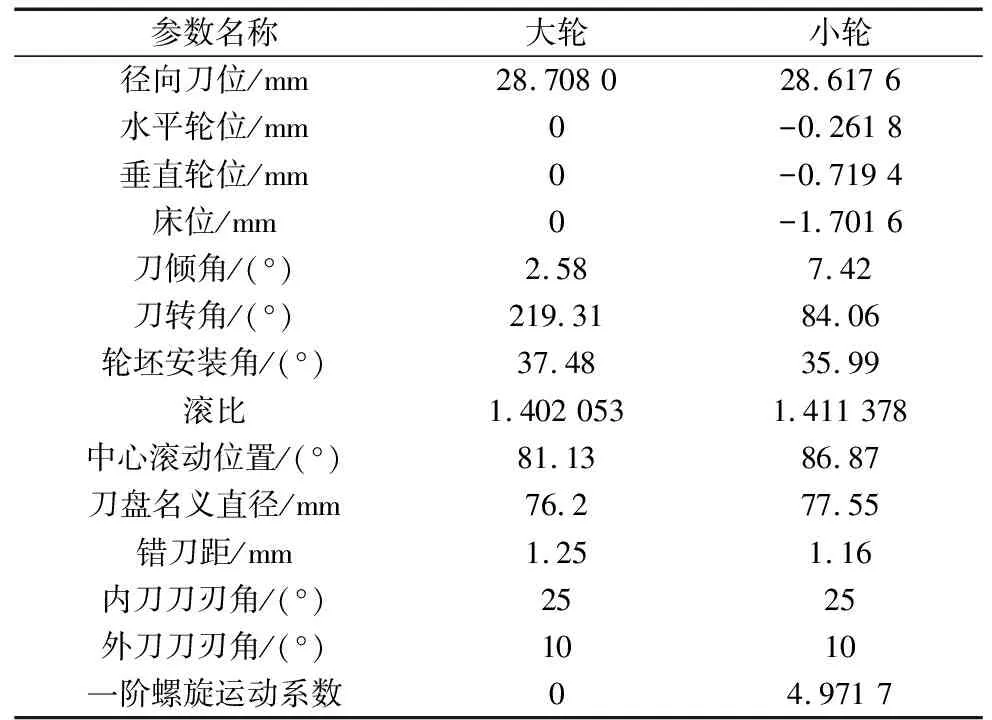
表2 机床调整参数
为了分析一至六阶螺旋运动系数对齿面形状的影响规律,假定一至六阶螺旋运动系数的改变量依次为:+0.2、+2、+20、+200、+2000、+20000。利用VB编制齿形分析软件,对每个改变量进行齿面误差计算并绘制齿面误差改变拓扑图。
计算分析结果如图3所示,图中粗实线表示理论齿面,细实线表示理论齿面低于实际齿面,细虚线表示理论齿面高于实际齿面,在齿轮凹凸两面的4个角点标有实际齿面在该点处相对于理论齿面的齿面误差值,误差值单位为μm。
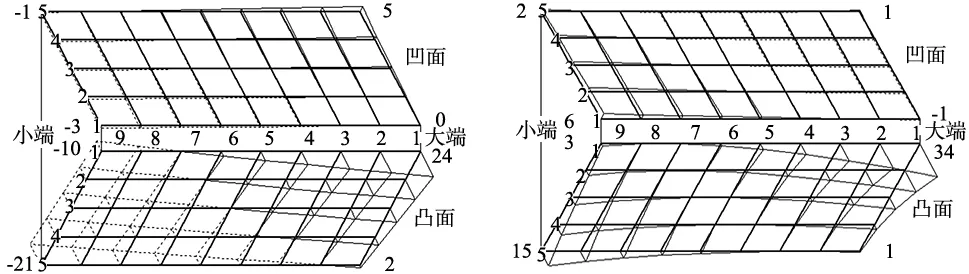
(a) 一阶螺旋运动系数改变+0.2 (b) 二阶螺旋运动系数改变+2
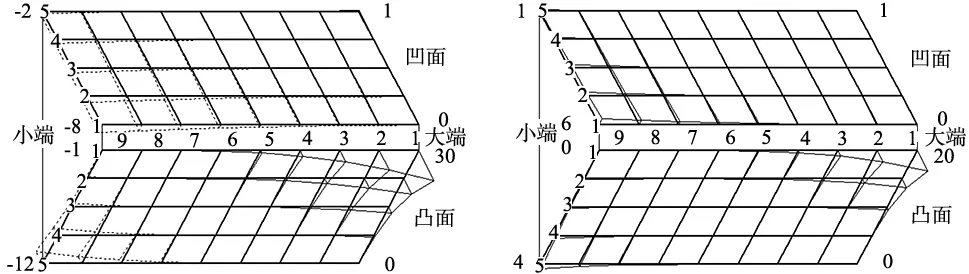
(c) 三阶螺旋运动系数改变+20 (d) 四阶螺旋运动系数改变+200
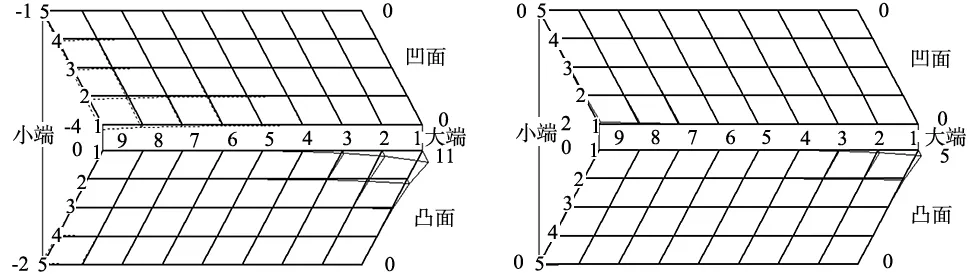
(e) 五阶螺旋运动系数改变+2000(f) 六阶螺旋运动系数改变+20000
4 螺旋运动系数对齿形的影响规律
在实际加工弧齿锥齿轮的过程中,为了指导操作人员根据滚动检查机的对滚结果,通过改变机床调整参数的方式,对齿轮副啮合区的大小、位置和方向进行精确的调整。不同的机床调整参数对齿面形状的敏感性和影响规律各不相同,将齿面误差对各阶螺旋运动系数的变化趋势分解为5个误差敏感系数。为了分析各加工参数改变量对齿面误差的影响程度,将齿面误差表示为二阶曲面的形式,如图4所示。
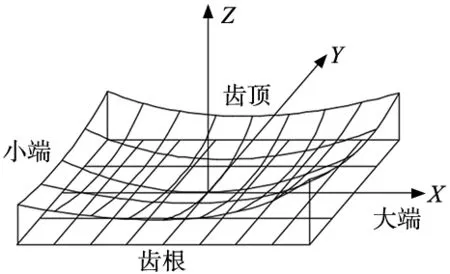
图4 齿面误差二阶曲面
图4中坐标系原点与齿面网格中点重合,齿长方向为X,齿高方向为Y,Z为齿面误差,用二阶曲面近似的表达齿面误差拓扑图,其表达式为:
Z=a1X+a2Y+a3XY+a4X2+a5Y2
(7)
式中:一阶系数a1、a2是对齿面倾斜角度的表达,a1为螺旋角误差敏感系数,影响齿长方向接触区的位置;a2为压力角误差敏感系数,影响齿高方向接触区的位置;二阶系数a3、a4、a5是对实际齿面弯曲程度的表达,a3为齿面挠率误差敏感系数,影响齿面接触区的对角程度;a4为齿长曲率误差敏感系数,影响齿长方向接触区的长短;a5为齿高曲率误差敏感系数,影响齿高方向接触区的宽窄。
将齿面网格上任意一点的齿面误差用矩阵表示为:
(8)
可化简为:
{Z}=[S]·{a}
(9)
式中:下标m为离散点个数,Z为齿面每个离散点对应的齿面误差,矩阵S为误差矩阵,其中数值由离散点的坐标确定,详细推导过程见文献[7]。每改变一项机床调整参数,与之对应的齿面误差Z也会随之发生改变,根据离散点坐标,可求得每个机床调整参数对应的误差敏感系数。式(9)为静定方程组,利用最小二乘法可求得其最小二乘解,即:
{a}=([S]T[S])-1[S]T
(10)
以上述齿轮副为例,分别计算小轮在各阶螺旋运动系数改变下凹凸两面齿面误差对应的误差敏感系数。计算结果如表3和表4所示。
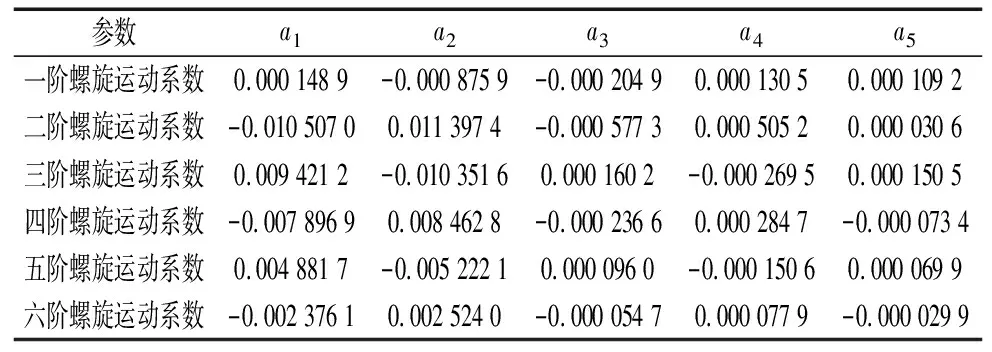
表3 小轮凹面各阶螺旋运动系数的误差敏感系数
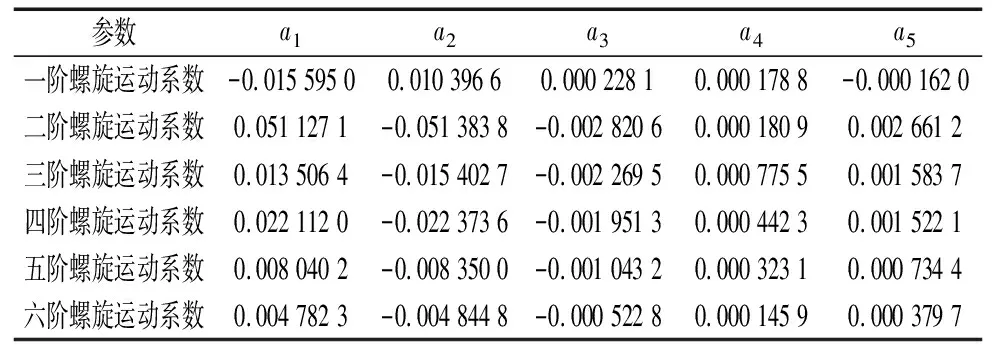
表4 小轮凸面各阶螺旋运动系数的误差敏感系数
误差敏感系数越大,则与之对应的各阶螺旋运动系数改变量对齿面形状的影响越大,结合图3对表3、表4的计算结果进行分析可知:
(1)螺旋运动系数对齿面的作用在于进行对角修形,且对凹面和凸面的影响程度不同,对凸面的影响明显大于对凹面的影响,对齿面的大小端比对齿面中部的影响更大。
(2)轮齿凹面的变化较为规律,改变一阶、三阶、五阶螺旋运动系数时的变化趋势相同,小端齿顶的实际齿面低于理论齿面,大端齿根的实际齿面高于理论齿面;改变二阶、四阶、六阶螺旋运动系数时的变化趋势相同,小端齿顶的实际齿面高于理论齿面,大端齿根的实际齿面低于理论齿面。
(3)轮齿凸面的大端齿顶在各阶螺旋运动系数改变时均高于理论齿面;改变一阶、三阶、五阶螺旋运动系数时的变化趋势相同,小端齿根的实际齿面低于理论齿面;改变二阶、四阶、六阶螺旋运动系数时,小端齿根的实际齿面高于理论齿面。
(4)轮齿凹面,各阶螺旋运动系数均对压力角影响最大,对齿高方向曲率影响最小;轮齿凸面,一阶螺旋运动对螺旋角影响最大,对齿高方向曲率影响最小,二阶到六阶螺旋运动对压力角影响最大,对齿长方向曲率影响最小。
为了验证论文分析结果的正确性,在H350GH数控螺旋锥齿轮磨齿机上,根据各阶螺旋运动的改变量进行了磨削试验,如图5所示。利用齿轮测量中心进行了齿面误差检测,如图6所示。检测结果与论文分析得到的结果基本一致,微小差别是由于加工误差与测量误差引起。因篇幅受限,论文仅列出二阶螺旋运动系数改变+2时的检测结果,如图7所示。

图5 H350GH数控螺旋锥齿轮磨齿机磨削实验齿轮 图6 齿轮测量中心检测实验齿轮

图7 实验测量结果(二阶螺旋运动系数改变+2)
5 结束语
本文在已有研究成果的基础上,建立了包含一至六阶螺旋运动系数的齿面数学模型,并基于数学模型探究了各阶螺旋运动系数对弧齿锥齿轮齿形的影响规律,得出以下结论:
(1)螺旋运动系数主要用于对角修形,其对轮齿凸面的影响明显大于对凹面的影响,对齿面的大小端比对齿面中部的影响更大。
(2)实验结果验证了齿面数学模型和软件分析的齿面误差拓扑图的正确性,为弧齿锥齿轮实际加工过程中接触区的调整和齿面误差的补偿提供了理论依据。
