基于改进SVM的新能源电站故障诊断方法

曹瑞峰，刘子华，袁 婷，罗扬帆，茹传红，秦 建，邢海军

（1. 国网浙江省电力有限公司，杭州 310007；2. 国网浙江省电力有限公司台州供电公司，浙江 台州 318000；3. 上海电力大学 电气工程学院，上海 200090）

0 引言

自从经济社会步入新时代，能源需求呈现增长迅速、需求刚性的特征，我国面临着经济发展需求与环境质量提升的双重压力。截至2021年底，我国可再生能源发电累计装机容量为10.6 亿kW，占全部电力装机容量的44.8%，其中水电装机3.91 亿kW，风电装机3.28 亿kW，太阳能发电装机3.06亿kW［1］。向高渗透率可再生能源转变已成为我国电力系统发展的必然趋势，而大量可再生能源接入对电力系统的运行和管理带来了巨大的挑战，新能源消纳问题将会成为未来电力系统主要任务之一。

新能源电站是以绿色电力［2］为主体的发电站，其二氧化碳排放量为零或趋近于零，主要包括：风力发电站、光伏电站、生物质能发电站、地热能发电站等。十三五期间新能源电站的规模迅速增长，但其发电小时数并没有同步增长。因为环境、气候、电网消纳等复杂因素的影响，许多新能源电站的发电时间明显低于理论值，这就需要研究新能源电站发电效益的提升技术，充分发挥存量绿色能源项目的效能［3-4］。但是，可再生能源发电机组具有模型多参数非线性、运行数据量庞大、运行工况多变的特性，这为研究带来了很大的挑战。文献［5］考虑到光伏阵列的非线性输出特性，提出了一种基于决策树的故障检测和分类方法，简化了发电模型多参数非线性导致的复杂诊断过程；文献［6］提出了一种基于k均值聚类和Apriori 算法的卷积神经网络故障诊断模型，并应用于风电机组的故障诊断，降低了对专家经验的依赖性；文献［7］提出了一种基于结合主成分分析法和支持向量机的风电机组齿轮箱故障诊断方法，解决了因数据量庞大引起的故障特征维度过高的问题；文献［8］提出了一种结合传统电压、电流定位法、时间跟踪描述和光伏电池参数估计模型的光伏组件故障诊断方法，用以判断热斑故障的发生位置和严重程度，综合考虑了多种故障特征，以适应实际运行中的复杂工况。

但以上文献仅侧重于某一问题的研究，未全面考虑新能源发电模型复杂度、数据量大小和多变工况的问题。本文从以上3个方面出发，提出了一种基于改进SVM（支持向量机）算法的新能源电站故障诊断模型。

SVM理论通过结构风险最小化原理和统计学习来提高分类能力［9］，目前已广泛应用于故障诊断领域［10-11］。本文首先分析了SVM 的概念和原理，并提出了一种基于决策级融合的改进SVM算法；然后，对光伏电站和风电站两类新能源电站的故障信号提取以及故障特征进行了研究，并在此基础上提出了新能源电站故障诊断模型；最后，利用MATLAB 仿真模拟，构建基于决策级融合的改进SVM故障诊断模型，并将新能源电站故障特征向量输入模型进行训练并验证。

1 新能源电站故障诊断方法

1.1 SVM

1995 年，Corinna Cortes 和Vapnik 提出了SVM的基本理论，用以处理二元分类问题，SVM主要是通过监督学习的方法实现对两类数据样本的分类，在数据样本较少的情况下，该方法也可以获得较好的效果［12］。SVM具有理论完备、分类识别能力强且结构简单的优点，因而在多个领域得到了广泛应用。

SVM的基本原理是利用事先选择的非线性映射将数据变换到一个高维特征空间中，这将线性不可分的数据样本在另一个高维空间中实现线性可分。这一过程的关键环节是要找到一个最优超平面，该超平面的主要作用是用来划分将要处理的数据样本［13］。针对一个二元分类的问题，其基本原理如图1所示，圆形和正方形分别代表两种不同类型的数据样本，L为两类样本的分界线，即超平面，超平面与最近的数据点之间的间隔为分离边缘，即图1 中的L1、L2。SVM 的最终目标就是要寻找一个特殊的超平面，使该超平面L 的分离边缘L1、L2最大，这个特殊超平面就是最优超平面。

图1 SVM最优超平面Fig.1 SVM optimal hyperplane

1.2 改进SVM

SVM是一种常用于解决具有少量数据样本的分类问题的技术。它最初是为了解决二元分类问题而提出的。然而，新能源电站故障类型识别是一个多类分类问题，故障类型不止两种。假设总共有k（k>2）种可能的故障类型，并定义所有可能的故障类型的集合。那么，光伏电站故障诊断就是一个k类分类问题。为解决这一问题，可以使用k（k-1）/2二元SVM分类器和一对一方法设计一个多类SVM。每个二元SVM 分类器都经过训练，通过使用分别表征两种故障类型的两类数据对两种故障类型进行分类。然后，k（k-1）/2二元SVM分类器的输出被一对一的方法用于生成k种故障类型的最终故障分类结果。

每个二进制SVM的输出是代表两种故障类型之一的类标签。这种方法有一定的局限性，即只能将输入故障特征确定性地映射到相应的故障类型，但不能提供概率信息融合所需的贝叶斯概率。为了实现所提出的故障诊断方法的概率信息融合，本文提出每个二进制SVM 使用如下Sigmoid 函数输出其分类的两种故障类型之一的贝叶斯概率，而不是故障类型的确定性类标签：

式中：μij表示当SVM对故障类型Fi和Fj进行分类时故障类型的概率；x是SVM 的输入特征向量，f(x)=ωTϕ(x)+b；ω和b是核函数的参数；φ（·）是SVM的核函数；参数G和H是通过最小化训练数据的负对数似然来获取的。输入特征属于k个故障类型中的每一个的概率pi（i=1，…，k）可以通过基于pairwise求解优化问题来确定耦合原则，多分类SVM的概率输出为式（2）的解。

式中：p=[p1，p2，...，pk]T。

基础多类分类器根据是否需要训练，有两种类型的组合器：不可训练组合器和可训练组合器。在单独训练基本分类器后，不可训练的组合器不需要训练。使用固定的组合规则，融合来自不同分类器的信息，并且假设所有分类器在确定最终结果时的权重都是相同的，所以不可训练组合器的主要限制是缺乏灵活性。但是，它比可训练组合器需要更少的训练数据。本文使用Dempster-Shafer理论［14］来设计不可训练的组合器。

可训练组合器，分类器的输出可以作为另一种学习算法的输入特征，该算法训练学习分类器输出的聚合函数数据而不是使用固定的组合规则。与使用不可训练组合器的信息融合相比，该方法能够从训练数据中提取更多信息。本文采用基于softmax回归方法［15］的简单可训练组合器。与不可训练组合器相比，可训练组合器的参数是从训练过程中学习的，通过该过程，可训练组合器可以学习最终诊断结果与分类器诊断结果之间的复杂关系。然而，可训练组合器的训练通常需要大量的训练数据集。

在实际的工作中，可根据不同的新能源电站所能获取到的历史数据的多少来选择具体的组合器，如果数据较少可以选择不可训练的组合器，若历史数据丰富则优先考虑可训练组合器。

2 新能源电站故障特征分析

2.1 光伏组件故障特征分析

影响光伏发电机组正常运行的因素很多，例如光照强度、入射角度等光照特征，安装角度、表面温度、电池已使用时间等光伏阵列特征，经纬度、海拔高度等位置特征以及气压、温度、相对湿度等天气特征［16］。在对光伏机组故障特征进行分析时，通常是把其中某些有较大影响的因素作为系统的修正特征来进行研究。其中，基于IV输出特性曲线的光伏组件故障诊断方法具有获取故障特征参数方便，判定容易的优点。因此，本文选择典型的I-V特征曲线作为光伏发电机组的故障特征。图2为处于正常状态下和某种故障状态下的光伏组件I-V输出特性曲线。

图2 光伏组件的I-V输出特性Fig.2 I-V output characteristics of PV modules

对光伏系统I-V输出特性曲线进行分析，可得到以下几种情况：

1）短路电流小于预期值。可能是因为封装材料变色发黄而导致透明度下降、恶劣天气使光伏板损坏而导致组件吸光能力不足等。以上现象使I-V曲线发生的变化与太阳辐照度减小类似。

2）开路电压小于预期值。引起开路电压减小的故障通常源于元件之间的互连关系，可能是由元件短路或旁路二极管发生故障造成，也可能是由于晶体硅组件的光致性能退化或电势诱发衰减效应［17］。

3）I-V曲线在开路电压侧切线斜率的绝对值变大。这一现象通常是因为光伏组件中的串联电阻增加而导致的。串联电阻增加的原因通常有元件之间的互连电阻增加、接线盒或连接器损坏、连接不良。

4）I-V曲线在接近短路电流侧切线斜率的绝对值变大。这一现象通常是因为光伏组件中的并联电阻下降导致，造成这一问题的原因通常是光伏组件或元件之间构成了并联回路、轻微的元件不匹配或者元件轻度变色［18］。

5）I-V曲线呈现出阶梯状。通常是由于旁路二极管的故障、元件损坏或者严重的元件失配而造成的。

通过以上分析可以发现，当光伏组件发生故障时，主要发生变化的输出参数有最大工作点电压Um和电流Im、开路电压Uoc以及短路电流Isc，因此，可以引入斜率k1、k2对组件故障状态进行识别。

式中：k1为最大功率点与开路点的斜率；k2为短路点到最大功率点的斜率。如图3所示。

图3 斜率k1、k2示意图Fig.3 Diagram of slopes k1 and k2

通过分析k1和k2的变化可以对光伏组件的故障状态进行判别。当k1和k2的值偏离正常范围时，即可认为光伏组件发生了相应的故障。即可依次通过比较最大功率点、开路点和短路点与其理论值的大小来判定故障类型。其中，第5种故障类型可由I-V特性曲线的形状直接诊断。根据以上原则判定组件所处的运行工况后，可进一步诊断故障的严重程度并进行定量分析。

2.2 风电机组故障特征分析

对于风力发电机来说，通常选用振动信号和电流信号来诊断齿轮箱和电机中发生的故障［19］。

2.2.1 振动信号中的故障特征

当齿轮出现故障时，会改变齿的刚度或改变其几何参数，从而导致振动信号的变化。这些变化调制了振动信号，可以表示为：

式中：m为啮合谐波数；fm为第m齿啮合谐波频率；Vm和θm分别为第m次啮合谐波的幅值和初始相位；am（t）和bm（t）分别为第m次啮合谐波的幅度和相位调制函数。

式中：fi（i=1，…，I）为第i个轴的旋转频率，I为齿轮箱的轴数；Amn和Bmn为幅度；αmn和βmn分别为第m啮合谐波的幅度和相位调制函数的第n谐波的初始相位。

振动信号中的故障特征可以在时域和频域中提取。本研究使用常用的时域特征为峰度和波峰因数。

峰度K为一个无量纲参数，定义如下：

式中：M4为第4个中心矩；σ4为信号的标准偏差。峰度表征信号的概率分布。如果信号服从正态分布，其峰度等于3，故障可能导致峰度增加。

波峰因数C定义为信号的最大绝对值与均方根值之比：

波峰因数说明信号有多“尖峰”。波峰因数越高，信号越尖。除了峰度和波峰因子之外，还有许多其他时域特征，例如形状因子和间隙因子。变速箱的不健康状态通常可以通过振动信号的时域特征与健康状态进行区分。然而，只使用时域特征通常难以诊断齿轮箱的故障类型。为了实现准确的故障诊断，需要对振动信号进行频域分析。齿轮箱振动信号频谱中的主要成分是齿轮啮合频率及其由轴旋转频率调制引起的边带。通常，边带数量和幅度的增加可能表明故障情况。因此，振动信号频谱中每个齿轮啮合频率fm及其边带fm±fi（i=1，…，I）处的能量可以作为故障特征。

2.2.2 电流信号中的故障特征

由于风力涡轮机传动系统中齿轮箱和发电机之间的机电耦合，发电机电流信号受到齿轮箱振动的调制。齿轮箱振动和发电机电流之间的关系可以从电机的转矩和电流关系推导出来［20］。如果齿轮箱以频率振动，发电机定子电流信号将包含基频分量f及其频率为f±fi的边带，当故障发生时，其幅度会发生变化。因此，可以选择f±fi处的能量作为电流信号中的故障特征。此外，由于齿轮箱的故障会在电流信号中激发更多的噪声，因此式（10）中定义的NSR（噪声信号比）也可以作为电流信号的故障特征。

3 基于改进SVM的故障诊断模型

3.1 光伏电站故障诊断模型

对于光伏电站的诊断模型，因其故障特征并不复杂，只需作出I-V曲线就可以明显的判断出故障类型。所以为了提高故障诊断的效率，增强故障诊断的实时性，用所提出的多类SVM分类器来构建其故障诊断模型。首先从光伏电站获取历史数据，然后从中提取出光伏电站历史运行过程中的I-V特征，将故障诊断作为SVM 分类器的输入，可以直接实现光伏电站多故障分类的目标，并且具有较高的准确率。但是这种诊断方法具有一定的局限性，所以在实际工作中需要根据各个电站的具体情况，考虑将其他的环境因素加入到诊断模型当中，经过适当改进后的诊断模型可以为电站运维人员提供较为准确的故障信息，以便工作人员及时修复电站中的各种故障及潜在故障，从而提高电站的发电效率。所提出的多类SVM模型用于设计光伏电站的故障诊断模型中，如图4所示。

图4 光伏电站的故障诊断模型Fig.4 Fault diagnosis model of PV power plant

3.2 风电机组故障诊断模型

传统故障诊断方法的准确性、可靠性和鲁棒性可以通过增加传感器的数量来提高。然而，这将增加系统的硬件成本和布线复杂性。本节提出的方法利用发电机电流信号和振动信号来进行故障诊断，这些信号可以在发电机控制系统中可获取，因此不需要安装任何额外的硬件。

将本文所提出的多类SVM模型用于基于电流SVM和振动SVM的风力发电机的诊断模型的中，如图5所示。诊断模型由4个功能模块组成。第一个功能模块是特征提取，它将齿轮箱振动信号和发电机电流信号中的故障特征分别提取到所提出的模型中。在第二个功能模块中，设计和训练一个电流SVM和一个振动SVM，分别根据从振动信号和电流信号中提取故障特征并输出每种可能的故障类型的概率。第三个功能模块是信息融合，它使用一个组合器来融合电流支持向量机和振动支持向量机的输出信息，即可能的故障类型的概率。最后一个功能模块将故障诊断为组合器输出中概率最大的故障。与传统方法相比，该方法可通过结合来自发电机电流信号和振动信号的信息以实现更高的故障诊断精度。此外，即使振动传感器或相关数据采集设备发生故障，所提出的方法也是有效的，因此可以提高诊断的可靠性和鲁棒性。

图5 风电机组的故障诊断模型Fig.5 Fault diagnosis model of the wind turbines

4 算例验证

4.1 光伏电站故障特征提取与诊断

1）故障样本分类

影响光伏发电系统正常运行的因素很多，关系十分复杂。因此，本文选择光照强度、环境温度、输出电流、输出电压及光伏组件温度作为光伏组件的特征选择参数，如表1所示。

表1 特征选择参数Table 1 Feature selection parameters

2）实例结果分析

光伏发电机组在光照强度不足的情况下无法正常运行，因此本文只提取每天07：00—18：00 的数据，并从中提取500组数据标记故障类型，部分基础数据和故障标记后的数据如表2所示。

表2 数据样本（部分）Table 2 Data samples （selected）

本节提出的SVM光伏组件故障诊断模型经过200组故障训练数据训练后，再对剩余测试数据进行准确率预测。训练过程如图6所示，平均准确率为99.43%。

图6 光伏电站诊断模型训练过程Fig.6 Training process of the diagnosis model of PV power plant

测试组数据共300组，正确分类291组，准确率为98.5%。诊断模型对故障状态类别对应的遮阴、短路、开路故障以及正常状态均能准确识别，但在识别老化故障时出现误判，有4组数据被误分到遮阴故障。这是因为发生老化故障时，光伏组件的开路电压与短路电流均不会改变，但最大功率点的电流、电压会有所减小，这一变化与遮阴故障特征类似，容易发生误判。

为了进一步验证本节提出的改进SVM算法在光伏组件故障诊断中的准确性，对同样的数据集又分别使用SVM 算法、PSO-SVM（粒子群优化支持向量机）和改进SVM 算法进行正确率对比验证，对比结果如表3所示。

表3 光伏诊断准确率比较Table 3 Comparison of PV diagnostic accuracy %

4.2 风力发电机故障特征提取与诊断

1）基础数据及特征信号提取

从齿轮箱和电机中提取的基本特征频率如表4所示。需要特征提取的一些参数如下：

表4 齿轮箱和电机的特征频率Table 4 Characteristic frequencies of the gearbox and motor

a）振动信号：波峰因数；峰度；f3，2f3，3f3，fm1±f1以及fm1±f2处的能量。

b）电流信号：NSR；f±f3，f±f2处的能量。

本文研究了4种不同的齿轮箱健康状况：齿轮箱健康、缺一齿故障、齿面剥落故障、裂纹故障。

2）实例结果分析

从具有4种不同齿轮健康状况的变速箱中提取信号数据。在每一个健康条件下，分别获取40 个齿轮箱振动信号和电流信号数据集。在40 个数据集中，28个用于训练两个多类SVM和可训练组合器，其余12 个用于测试所提出的方法。电流改进SVM 和振动改进SVM 输入分别是从齿轮箱振动和双馈定子电流信号中提取的故障特征，如图7、图8所示。

图7 齿轮箱的振动信号及其功率谱密度Fig.7 Vibration signals of the gearbox and its power spectral density （PSD）

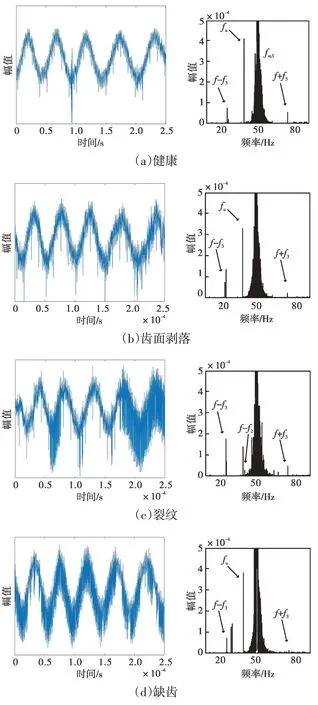
图8 双馈电机的电流信号及其功率谱密度Fig.8 Current signals of the doubly-fed motor and its power spectral density （PSD）

图7（a）显示了齿轮健康时振动信号的PSD（功率谱密度）。在这种情况下，由于传动平稳，因此只有啮合频率fm1和输出轴旋转频率f3占主导地位。图7（b）显示了被测齿轮齿面剥落时振动信号的PSD，fm1和f3处的能量增加。此外，边带fm1+f1以及f3的二次和三次谐波变得更加明显。图7（c）显示了裂纹情况下的结果，与健康情况相比，fm1处的能量高且边带fm1+f1以及谐波2f3更明显。对于图7（d）所示的缺齿情况，与健康状态相比，除了f3和2f3处的能量增加外，fm1-f2和一些未知频率分量也被激发。总之，齿轮故障会引起额外的振动或改变现有振动的幅度，然而并没有清楚地显示出不同故障类型之间的差异。

图8（a）显示了齿轮健康时电流信号的PSD。在齿面剥落和齿面裂纹的案例中，f±f3分量很明显，并且振幅在f-f3处增加，分别如图8（b）和（c）所示，f-f2分量也在齿面裂纹的情况下被激发。在图中有一个非常明显的频率分量，被标注为fu，但其与任何齿轮箱故障无关。再次，不同齿轮故障类型之间没有明确的差异。因此，故障类型不能直接通过振动或电流信号的PSD频谱来判断。

为了应对这一挑战，将所提出的方法应用于齿轮故障的诊断。该方法使用两个具有概率输出的多类SVM，分别根据从齿轮箱振动信号和双馈定子电流信号中提取的特征，自动计算每种故障类型的可能性，然后融合两个SVM 的概率输出，得到最终的故障诊断结果。基于此诊断模型的训练过程如图9所示，基于可训练组合器与不可训练组合器模型的样本集的平均准确率分别为99.76%和97.53%。

图9 风电站诊断模型训练过程Fig.9 Training process of the diagnosis model of wind farm

训练结束后，输入测试数据集进行诊断。在特征级融合方法中，振动信号和电流信号中提取的特征直接由SVM分类器用于输出每种故障类型的概率。每种健康状况都有12个数据集用于测试。因此，总共有48 个测试数据集。将所提出的基于改进SVM的信息融合方法的故障诊断准确性与仅考虑振动信号的改进SVM、仅考虑电流信号的改进SVM的故障诊断准确性进行了比较。振动改进SVM 和电流改进SVM 的故障诊断准确率分别为93.75%和91.67%；当使用特征级融合和提出的决策级融合下的可训练和不可训练融合方法时，准确率分别提高到97.92%、96.63%和99.54%。这些结果表明，与使用单一类型信号的方法相比，特征级融合和所提出的基于决策级融合的故障诊断方法都可以提高诊断准确性并降低错误故障诊断率。

为了进一步验证改进SVM算法在风电机组故障诊断中的准确性，对同样的数据集又使用PSOSVM算法和改进SVM算法进行正确率对比验证，对比结果如表5所示。结果表明，本文提出的改进SVM算法具有较优的故障诊断效果。

表5 风机故障诊断准确性比较Table 5 Comparison of fault diagnosis accuracy of wind turbines %

5 结语

本文针对新能源电站在实际运行中可能出现的几种故障，采用多元SVM 分类算法对SVM 进行优化，提出了基于改进SVM算法的新能源电站故障诊断模型并输入故障特征向量，获得对新能源电站正常工作状态以及各种典型故障状态的分类识别。实验结果表明，改进后算法的分类效果得到明显提高，光伏电站的故障诊断准确率由96.5%提高到98.5%；对于风电站的故障诊断，仅使用单一振动信号或电流信号时准确率仅有93.75%和91.67%，采用所提出的决策级融合下的可训练和不可训练融合方法时，准确率提高到96.63%和99.54%。本文所提诊断方法和模型对新能源电站故障能够得到较优的诊断效果，诊断准确率有所提高。