制造业集聚、异质性投资与黄河流域能源环境效率

岳 立 高先巧

（兰州大学经济学院，兰州 730000）

引 言

二十大报告指出“实现碳达峰碳中和是一场广泛而深刻的经济社会系统性变革。立足我国能源资源禀赋，坚持先立后破，有计划分步骤实施碳达峰行动。完善能源消耗总量和强度调控，重点控制化石能源消费，逐步转向碳排放总量和强度‘双控’ 制度。深入推进能源革命，加快规划建设新型能源体系，坚持把发展经济的着力点放在实体经济上，推进新型工业化。加快建设制造强国”。在绿色发展的要求下，通过提高能源环境效率来追求低碳经济转型，实现生态环境改善与能源消耗之间的平衡，已成为地区高质量发展进程中一个紧迫的问题。黄河流域能源资源十分丰富，中下游的石油、煤炭和天然气，在全国占有非常重要的地位，但存在资源开发与生态环境保护矛盾以及产业同构现象明显，缺乏较强竞争力新兴产业集群。虽然黄河流域能源资源密集，但是作为我国重要的工业基地，其资源环境承载能力弱，生态环境风险隐患突出。沿黄各地区产业存在低质低效问题，并且支撑高质量发展的资金外流严重，要素资源缺乏。基于此，厘清黄河流域制造业集聚与能源环境效率的关系以及各类投资的作用对促进沿黄河各城市高质量发展、防范化解生态环境风险具有重要意义。

现有文献对产业集聚与能源效率的关系进行了较丰富的实证研究，但结果存在不同。一些研究认为产业集聚有利于能源效率的提高，典型的有Qu 等（2020）［1］通过动态空间计量模型实证分析表明金融集聚对能源效率具有积极影响。但也有一些研究认为产业集聚抑制了能源效率的改进，如张平淡和屠西伟（2022）［2］发现制造业集聚对能源效率存在负向影响。除此之外，相关文献还认为产业集聚同能源效率存在非线型关系。其中，Wu 和Lin （2021）［3］通过面板门槛模型识别出钢铁行业聚集与能源服务效率之间的非线性关系。由于能源消耗过程中产生的污染排放并非局部环境问题，会通过大气、河流、交通、集聚等自然因素或经济机制对邻近区域造成影响［4］。在研究方法上，若忽略区域间存在的空间相关性和溢出效应，选择普通面板模型进行估计，会导致估计结果出现偏差。因此，有必要引入考虑空间效应的计量模型进行实证分析。大多文献集中于中国对外投资或外商直接投资对能源的影响。如屈小娥等（2018）［5］运用面板门槛模型，验证了中国对外直接投资对能源环境效率的影响具有单门槛特征；景守武和陈红蕾（2018）［6］运用系统GMM证明了外商直接投资对能源环境效率存在正向影响；Li 等（2019）［7］研究得到外商直接投资可以增强能源强度收敛；Wang 等（2021）［8］构建动态空间计量模型，探索了外国直接投资通过提高能源强度间接影响碳排放的机制。在当前文献中关于内资、外商投资与港澳台投资对能源环境效率的综合研究鲜见。研究不同类型投资通过制造业集聚对能源环境效率影响的异同，有助于认识不同投资与环境保护的统一，验证各类投资是否通过制造业集聚存在跨区域污染效应。

1 模型设定、变量与数据来源

1.1 模型设定

1.1.1 空间Tobit 杜宾模型

由于能源环境效率会受到本地区和邻近地区制造业集聚的共同影响，目前学者研究产业集聚与能源效率的实证关系多使用空间杜宾模型，但由于能源环境效率是取值范围在［0，1］之间的截断数据，使用普通的空间杜宾模型会导致估计量不一致。因此，本文构建空间Tobit 杜宾模型，设定如下：

其中，因变量EEEit表示区域i在t年的能源环境效率，自变量Aggit表示区域i在t年的制造业集聚水平，CV是控制变量集，μ是随机扰动项的空间误差，W代表空间权重矩阵。ρ是空间滞后项系数，反映因变量的空间相关性。λ是扰动项空间误差系数，反映误差结构中存在的空间依赖性即区域间的空间关联。

1.2 变量选择

（1） 被解释变量：能源环境效率。能源环境效率可以理解为每单位的经济要素投入创造更多的经济产出和更少的污染排放的水平，能够较好刻画经济增长与环境、气候治理平衡发展程度［9］。本文选取年末第二产业从业人数表征劳动力投入。通过固定资产投资价格指数，以2006 年为基期，对当年固定资产总投资规模进行调整，使用永续盘存法估算城市每年资本存量作为资本投入。能源涵盖城市消耗的3 种能源，即天然气、液化石油气和电力，各城市一次能源的消费量按照能源折标准煤系数换算成统一能源单位作为能源投入［5，10］。期望产出是以2006 年不变价格下通过工业生产者价格指数进行平减的实际工业生产总值，非期望产出包括工业废水排放、工业二氧化硫排放、工业烟粉尘排放以及二氧化碳排放。其中二氧化碳排放量通过碳排放系数进行估算［11］。非径向方向距离函数［12，13］表示为：

本文投入产出效率的指标包括3 种投入，1 项期望产出，4 项非期望产出，具体见表1。假设投入、期望产出和非期望产出对效率的影响同等重要，选取权重向量为w＝（1／9，1／9，1／9，1／3，1／12，1／12，1／12，1／12）T。

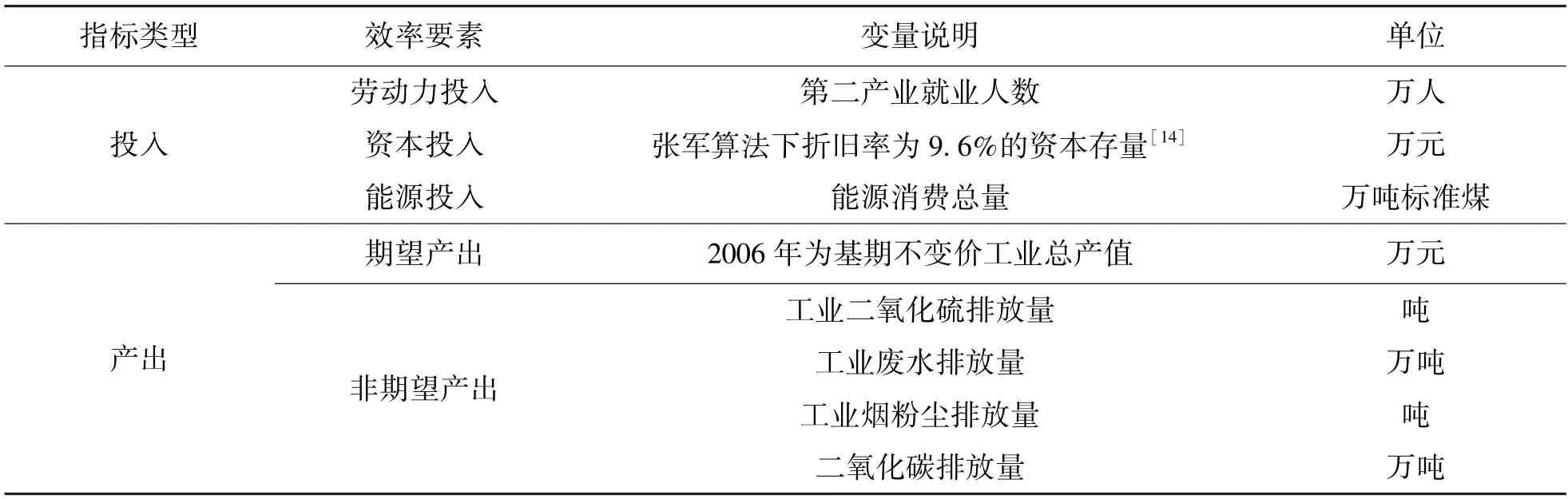
表1 效率投入产出指标

（2） 解释变量：制造业集聚（Agg）。在产业集聚研究中，区位熵可以消除区域规模的差异，反映产业部门的专业化程度，衡量一个产业部门在区域生产结构中相对于国家水平的相对优势［15］。本文采用区位熵测度各城市的制造业集聚水平，其测算方法具体如下：

本文使用就业人数作为衡量制造业集聚的区位熵指标。其中，eij为j城市制造业就业人数；ej为j城市年末单位从业人员数；ei为全国制造业就业人数；e为全国总就业人数。

（3） 机制变量：本文选取规模以上内资企业工业总产值与内资投资企业数量的比值来衡量内资投资水平（DI）；用规模以上外商投资企业工业总产值与外商投资企业数量的比值来衡量外商投资水平（FI）；用规模以上港澳台商投资企业工业总产值与港、澳、台商投资企业数的比值来衡量港、澳、台商投资水平（HI）。

（4） 控制变量：环境规制（Regu）：使用工业固体废物综合利用率来衡量环境规制［16］。产业结构（Str）：用第三产业占GDP 比重衡量产业结构［17］。政府支持（Gov）：用政府科技支出占财政一般预算内支出的比重代表政府支持创新的力度［18］，比重越大，表明该地区越重视科技发展。基础设施水平（Inf）：用人均城市道路面积衡量城市基础设施建设程度［19］。

鉴于部分地区数据获取困难，本文剔除了数据缺失严重的州、盟，最终以黄河流域56 个地级市2006～2021 年的数据为样本。具体描述性统计结果见表2。本文初始数据主要来源于《中国城市统计年鉴》，部分数据整理自各地级市的统计年鉴，为保证数据的完整性，少量残缺数据使用线性插值法填补；国家就业人数、工业生产者价格指数、GDP 平减指数来源于国家统计局；能源折标准煤参考系数来源于《中国能源统计年鉴》。

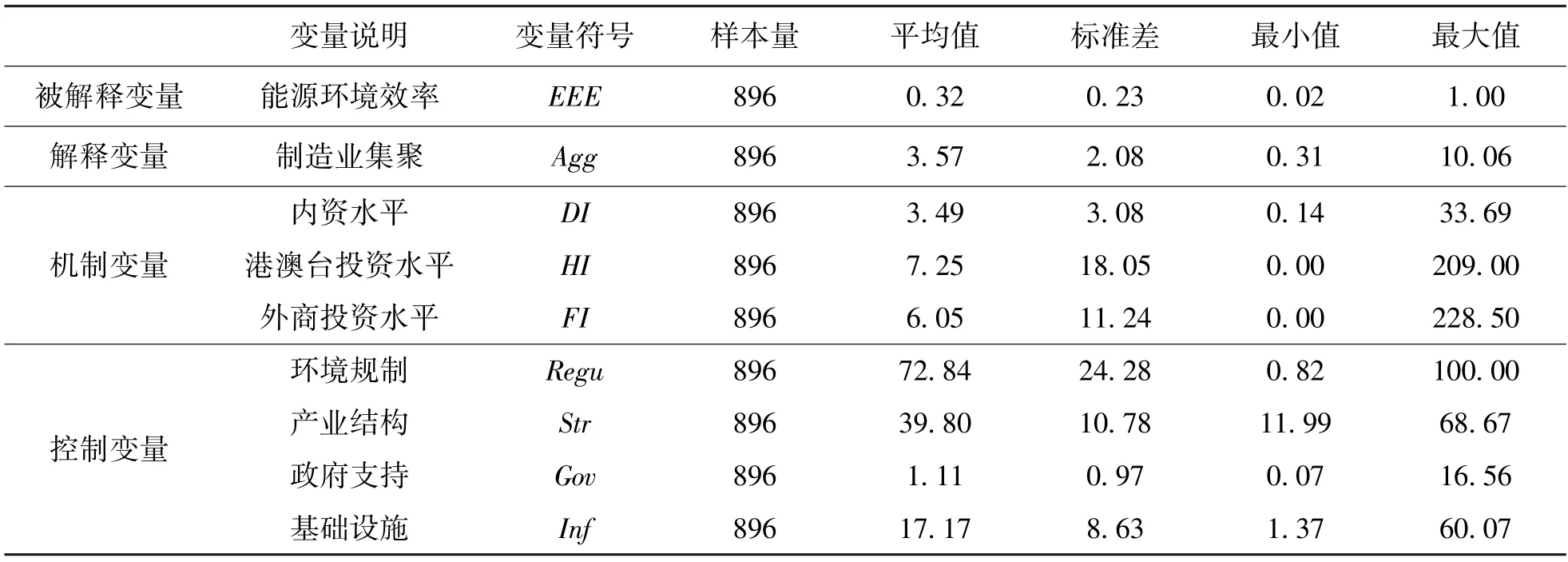
表2 描述性统计

2 实证估计与结果分析

2.1 基准结果

2.1.1 空间相关性检验

通过莫兰散点图可以看出（见图1），多数城市分布在第一象限与第四象限，自变量与因变量均存在空间正相关性，呈现“高高” 集聚、“低低” 集聚的现象。能源环境效率2006 年空间正相关性强于2021 年，说明能源环境效率的空间辐射作用呈现波动下降趋势。制造业集聚2006 年空间正相关性弱于2021 年，说明制造业集聚的空间辐射作用呈现波动上升趋势。基于地理距离权重矩阵的全局莫兰检验结果显示（见表3），除2012 年能源环境效率的莫兰指数在10%水平上显著外，2006～2011 年、2013～2021 年能源环境效率的莫兰指数均在5%水平上显著为正；2006～2021 年制造业集聚莫兰指数均在在5%水平上显著为正。以上表明模型的核心变量具有很强的正空间依赖性。因此，本文有必要构建空间计量模型进行实证分析。

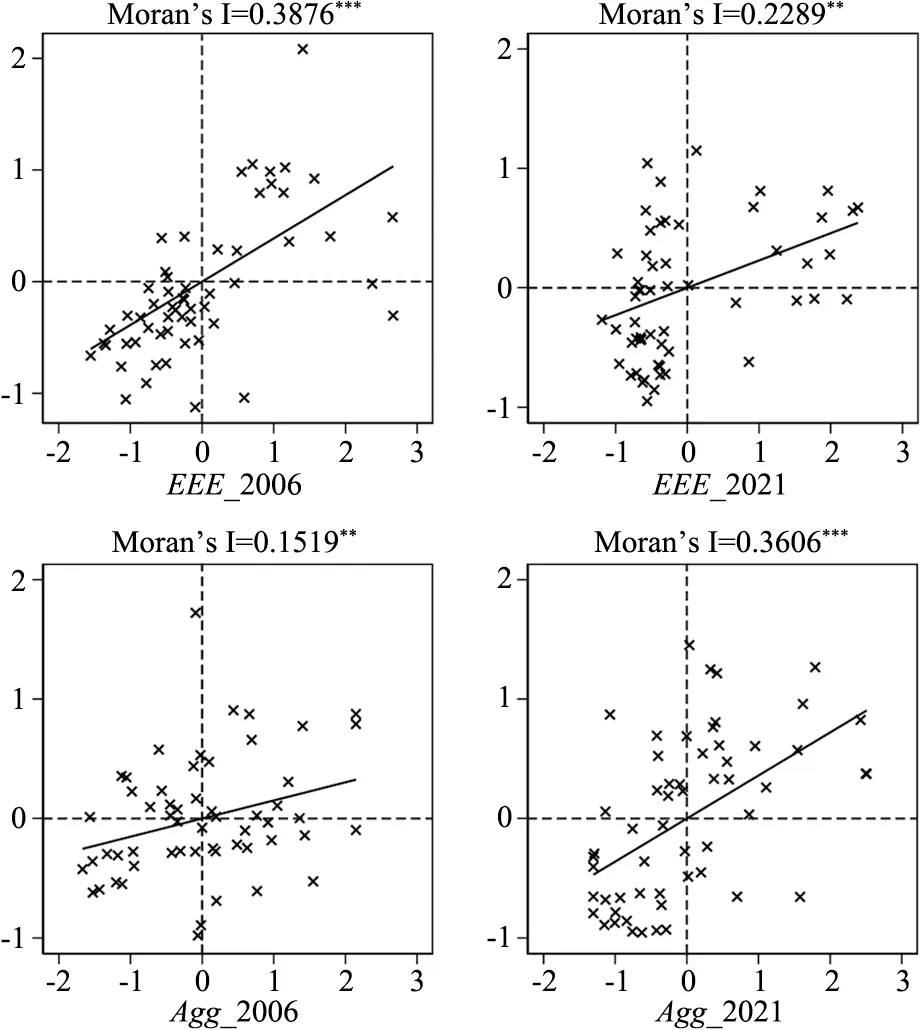
图1 能源环境效率、制造业集聚莫兰散点图

2.1.2 回归结果分析

模型1 为混合回归模型，模型2 为空间Tobit杜宾模型。与普通面板回归结果相比，制造业集聚对能源环境效率的影响存在显著的空间外溢效应。地理距离权重矩阵下空间相关系数ρ在统计上高度显著，进一步验证了能源环境效率空间依赖性的存在。从模型2 的结果可知（见表4），制造业集聚对能源环境效率的影响一次项系数在5%的显著性水平上为正，二次项系数在1%的显著性水平上为负，两者在统计上存在倒U 型曲线关系，拐点为4.29。这说明本地区制造业集聚水平小于4.29 时，集聚区内基础设施日渐完善，企业间的联系逐渐密切，降低了交易成本，缩短了知识传播渠道，有利于本地区能源环境效率的提高；本地区制造业集聚水平超过4.29 后，城市制造业逐渐向过度集聚演变，集聚水平超越最优规模，同行业过度竞争、环境污染等拥挤效应会引致制造业向外转移，并且为避免技术泄漏，制造业企业可能会减少外部合作，阻断知识和技术溢出渠道，不利于本地区能源环境效率的提高。因为地区之间地理空间相邻，制造业集聚产生的知识溢出会对邻地产生影响。从空间溢出效应来看，w×Agg的估计系数为负且通过了1%的显著性水平检验，w×Agg2的估计系数为正且通过了5%的显著性水平检验，周边地区制造业集聚与本地区的能源环境效率在统计上存在正U 型关系，拐点为5.1。这说明邻地的制造业集聚水平小于5.1 时可能会存在抢占本地区制造业集聚发展的资源，遂不利于本地区能源环境效率的提高；邻地制造业集聚水平发展超过5.1 时可能会分担一部分本地区制造业过度集聚引致的资源拥挤，从而有利于本地区能源环境效率的提高。

2.2 内生性处理

为试图减轻本文模型可能存在的内生性所造成的潜在估计偏差，参考袁华锡等（2022）［20］、Jin和Lee （2013）［21］的研究，使用将各解释变量及其空间滞后项作为工具变量进行模型估计的广义空间两阶段最小二乘法（GS2SLS）来处理模型内生性（见表4 模型3）。对于核心变量，参数估计结果并未发生明显改变，与基准分析基本保持一致。

2.3 稳健性检验

（1） 重新测度被解释变量。将NDDF 中权重向量设置为w＝（0，0，1／3，1／3，1／12，1／12，1／12，1／12）T，分解出劳动与资本投入的无效率项来度量能源环境效率［22］；（2） 更换核心解释变量。利用赫芬达尔指数（HHI）对制造业集聚进行重新测算［23］；（3） 更换空间权重矩阵。通过构造邻接矩阵、经济矩阵、经济地理矩阵进行稳健性分析［24］。从稳健性结果来看，无论是重新设置权重向量、改变集聚测度方法还是替换空间矩阵并没有改变本文主要发现，证实了上文基准结果是稳健的。限于篇幅，结果表略。

2.4 机制分析

本文进一步从内资、港澳台投资、外资3 个角度来检验异质性投资对能源环境效率的影响（见表5）。模型4 报告了各类型投资与能源环境效率的经济关系，模型5 报告了各类型投资和制造业集聚对能源环境效率是否存在共同影响的检验结果。模型4 结果显示，总体上内资、港澳台投资、外资均在1%的水平上显著对能源环境效率存在积极的直接影响。其中内资影响最大，外资次之，港澳台投资影响最小。模型5 结果显示内资与制造业集聚共同对能源环境效率在1%的显著性水平上存在倒U 型经济影响，表明内资与制造业集聚的共同影响先是有利于能源环境效率的提高，然后可能会因为投资过度集聚导致产业过度竞争而造成能源环境效率的降低。可见，要持续保持内地投资目前积极的优势，调整内地投资的产业结构，将资金更多投向新兴制造业，推动清洁生产，以此来强化制造业集聚对能源环境效率的积极作用；港澳台投资与制造业集聚共同对能源环境效率存在显著的正U 型经济影响，表明港澳台投资与制造业集聚的共同影响先是不利于能源环境效率的提高，跨过门槛值之后，变为积极影响。可能的原因在于港澳台投资通过制造业集聚存在一定的跨区域污染效应；外商投资与制造业集聚共同对能源环境效率存在显著的线性影响，表明外商投资的增加和制造业集聚程度的提高对能源环境效率会产生正向影响。这意味着制造业集聚对能源环境效率的积极作用会随着外商投资的增大得到加强。相比于港澳台投资，内资、外商投资与制造业集聚能发挥正向作用可能由于更加注重制造业环境规制的要求与地区的环境监管、有相对成熟的环保理念和先进的环保技术，可以在促进制造业发展的同时减少能源使用和污染物排放。

表5 机制分析结果

2.5 区域异质性分析

本文将涉及的黄河流域56 个城市根据位置划分为3 个子样本①：上游、中游和下游。同样使用空间Tobit 杜宾模型进行区域异质性分析，结果见表6。上游空间相关系数ρ在1%的水平上负显著，说明上游地区能源环境效率空间差异大，呈现“高低”、“低高” 集聚，但制造业集聚与能源环境效率依然存在正U 型关系，拐点为7.27。从非空间计量来看，平方项系数不显著，制造业集聚与能源环境效率不存在非线性关系。中游空间相关系数ρ在1%的水平上显著为正，制造业集聚对能源环境效率存在显著的倒U 型影响，拐点为4.5。从空间溢出效应来看，邻地制造业集聚对本地能源环境效率存在显著的正U 型影响，与基准结果一致。下游的空间相关系数ρ在1%的水平上显著为正，但制造业集聚与能源环境效率之间不存在显著的经济关系。对比不同河段制造业集聚对能源环境效率的影响拐点来看，中游拐点值比上游拐点值小。其拐点存在差异可能的原因是地理条件、资源禀赋、制造业基础、区域分工与协同发展等方面存在不同。上游城市生态环境脆弱，主要功能是涵养水源，以原材料加工、农牧业等传统产业为主。中游城市产业基础较好，主要布局着能源、化工、建材等加工制造业，制造业集聚水平高，同等水平的制造业在中游集中能较早的越过拐点，促进能源环境效率的提高，在上游反而会阻碍能源环境效率的发展。综上，制造业集聚对黄河流域能源环境效率的影响存在区域异质性。其原因可能是上游制造业集聚水平较低，城市之间相隔较远，中间由山地相连，城市聚集产生的大气污染很难向其他城市扩散，所以制造业集聚对能源环境效率在空间上呈现负显著。中游地势相对平缓，集聚水平较高，城市分布较为紧密，制造业集聚生产活动排放的大气污染物容易向邻近区域扩散，导致制造业集聚对能源环境效率在空间上的影响显著。下游是地上悬河，平原地区受悬河、洪水威胁，分布低山丘陵，不适合大规模制造业集聚。

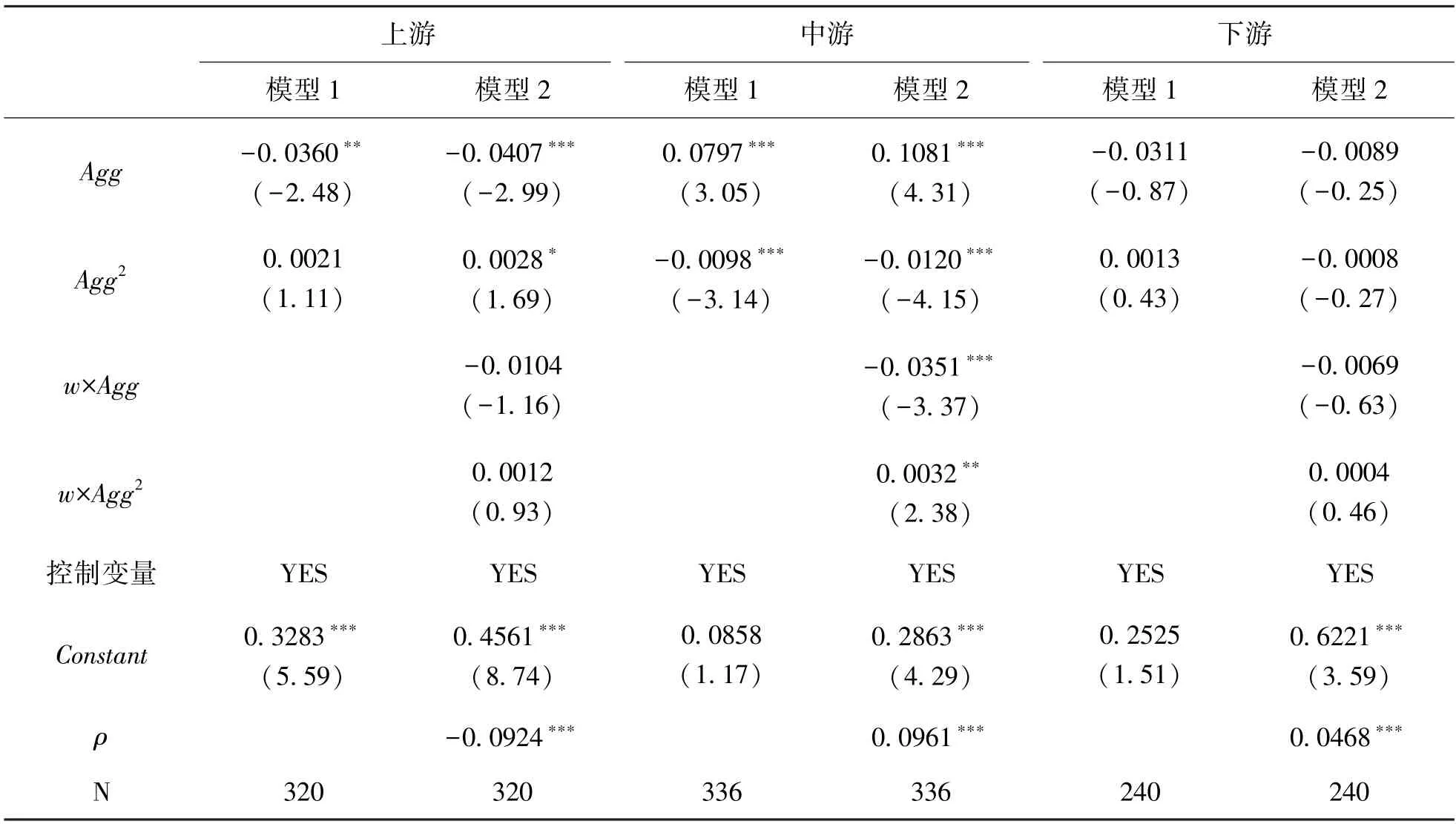
表6 区域异质性结果

3 结论与建议

3.1 研究结论

提高能源环境效率是推动黄河流域绿色低碳发展和能源转型的重要内容，分析制造业集聚与能源环境效率的非线性关系，以及3 种类型投资发挥的作用，对于有序推进制造业降碳、减污、扩绿、增长协同具有重要的现实意义。本文以2006～2021 年黄河流域56 个城市数据为例，运用非径向方向距离函数对能源环境效率进行测算，构建空间Tobit 杜宾模型识别了制造业集聚、3 种类型投资与能源环境效率的经济关系，并采用3 种不同方式对模型进行稳健性检验。结论如下：

本地区制造业集聚和能源环境效率存在倒U型关系，邻近地区的制造业集聚对本地的能源环境效率具有正U 型空间溢出效应。机制分析发现，不同投资在制造业集聚与能源环境效率的经济关系中发挥着不一样的作用。内资发挥着正向作用，同制造业集聚与能源环境效率存在倒U 型经济关系。港澳台投资同制造业集聚对能源环境效率发挥着正U 型影响；外资同制造业集聚与能源环境效率存在正的线性关系。分河段的异质性分析发现，上游、中游和下游均显示能源环境效率存在显著的空间相关性，相比于中、下游，上游能源环境效率存在负空间关联。上游制造业集聚与能源环境效率存在正U 型关系。中游制造业集聚对能源环境效率存在倒U 型影响。下游城市制造业集聚对能源环境效率的影响不显著。

3.2 政策启示

（1） 基于制造业集聚对能源环境效率的影响存在拐点。制造业企业应加强科技研发，重视清洁生产技术的投资，切实推动能源低碳技术在制造业中的运用，加快制造业绿色转型；另外，政府应合理规划制造业布局，将集聚规模控制在合理范围，避免盲目无效的制造业扎堆，造成资源拥挤，把制造业生产活动限定在资源环境可承受范围内；加大对科学技术的投资，发展新兴制造业，推动清洁生产，走绿色、可持续发展之路。

（2） 不同类型资本在制造业集聚与能源环境效率之间发挥了作用，政府在招商引资的过程中应合理利用各类型投资的优势。加强国际、地区间的合作，并鼓励外商投资企业顺应本地经济发展趋势，更多投向高端制造、智能制造和绿色制造，助推能源转型升级，支持内资、港澳台投资企业探索制造业清洁生产的新模式。

（3） 由于各河段制造业集聚与能源环境效率的经济关系存在差异，黄河流域应关注制造业集聚的区域差异化发展。增强流域内可持续高质量发展动力，紧密结合各河段比较优势，鼓励更多制造业生产活动聚集在中游，促进上、中、下游各区域合理分工，以生态保护为前提优化调整制造业空间布局，巩固壮大流域内实体经济根基，在关注制造业对经济增长的带动的同时还要重视其对能源环境效率的改进。

注释：

①本文涉及的黄河流域56 个城市包括上游20 个城市：巴彦淖尔、白银、包头、定西、鄂尔多斯、固原、呼和浩特、兰州、陇南、平凉、庆阳、石嘴山、天水、乌海、乌兰察布、吴忠、武威、西宁、银川、中卫；中游21 个城市：宝鸡、焦作、晋城、晋中、临汾、洛阳、吕梁、三门峡、朔州、太原、铜川、渭南、西安、咸阳、忻州、延安、阳泉、榆林、运城、长治、郑州；下游15 个城市：安阳、滨州、德州、东营、菏泽、鹤壁、济南、济宁、开封、聊城、临沂、濮阳、泰安、新乡、淄博。其余州、盟因数据获取困难，未纳入本文研究中。