与双曲线渐近线有关的一组优美性质

广东省中山市中山纪念中学(528400) 谢林涛

双曲线是圆锥曲线中的重要组成部分,双曲线与椭圆、抛物线不同之处是双曲线拥有两条渐近线,所以围绕双曲线的渐近线去设置问题是高考的一个重要考查方向,与双曲线的渐近线有关的性质和题目也是层出不穷. 笔者在研究过程发现与双曲线渐近线有关的一组优美性质,分享如下.

一、准备知识

二、双曲线中与渐近线有关的一组性质

结论2.1已知双曲线O为坐标原点,M(x0,y0)为C上任意一点,C在点M(x0,y0)处的切线与双曲线得两条渐近线分别交于点P,Q, 则(1)∆OPQ的面积为定值ab;(2)M为PQ的中点.

证明(1) 设切点M(x0,y0), 则由上文1.1 得知, 切线与渐近线联立,解得

所以且∆OPQ的面积

(2)xP+xQ=a2b·= 2x0,所以点M为PQ的中点.

结论2.2已知双曲线= 1(a> 0,b> 0),O为坐标原点,M(x0,y0)为C上任意一点,过点M作C的两条渐近线平行的直线,分别交两条渐近线于A,B两点,则(1)∆OAB,∆OMA,∆OMB,∆MAB,的面积为定值(2)平行四边形OAMB的面积为定值

证明由结论2.1 可知,MA,MB为∆OPQ的中位线,所以容易得到∆OAB,∆OMA,∆OMB,∆MAB的面积为∆OPQ的面积的,即于是平行四边形OAMB的面积为定值

结论2.3已知双曲线= 1(a> 0,b> 0),O为坐标原点,M(x0,y0)为C上任意一点,过点M作C的两条渐近线的垂线,垂足分别为R,S,则(1)|MR|·|MS| =(2) ∆MRS的面积为定值; (3) ∆ORS的面积为,当a=b,即双曲线C为等轴双曲线时,∆ORS的面积为定值

证明(1)点M(x0,y0)到渐近线的距离d1=到渐近线的距离于是|MR|·|MS|=d1d2=

(2)

又因为

(3)因为

当a=b,代入上式得∆ORS的面积为定值

结论2.4已知双曲线= 1(a> 0,b> 0),O为坐标原点,M(x0,y0) 为任意一点, 直线l过点M,且与C交于P,Q两点, 与C的两条渐近线交于G,H两点, 若M为PQ的中点, 则(1)M为GH的中点; (2)∆OGH的面积, 当点M(x0,y0)在双曲线=λ上(λ为不等于1 的常数) 时,S∆OGH=|λ|ab.

证明(1) 由准备知识可知, 直线OM与直线l的斜率之积, 所以, 于是直线l方程为:, 与渐近线联立, 解得,同理可得,所以

所以M为GH的中点.

评注实际上,由又点M(x0,y0)在双曲线上, 我们可知直线l为双曲线E在点M(x0,y0)处的切线. 于是我们有下面结论.

结论2.5已知双曲线=1(a>0,b>0),O为坐标原点,M(x0,y0)为双曲线E:=λ(λ≠1)上任一点,双曲线E在点M处的切线l与双曲线C的两条渐近线交于G,H两点,则S∆OGH=|λ|ab.

证明因为双曲线C,E共渐近线,双曲线λ(λ≠1)方程可化为

由结论2.1 可知S∆OGH=|λ|ab.

结论2.6已知双曲线= 1(a> 0,b> 0),O为坐标原点,M(x0,y0) 为双曲线C上任意一点, 过点M(x0,y0)作双曲线=λ(λ<0 或λ>1)的两条切线,切点分别为A,B,直线AB与双曲线C两条渐近线交于G,H两点,则S∆OGH=λ2ab.

证明由准备知识直线与渐近线联立, 解得同理可得于是

三、结论应用

例1(2023 届T8 联考)已知双曲线1 (a> 0,b> 0) 的左右焦点分别为F1,F2,O为坐标原点, 过F2作渐近线的垂线, 垂足为P,若则双曲线的离心率为____;又过点P作双曲线的切线交另一条渐近线于点Q,且∆OPQ的面积则该双曲线的方程为____.

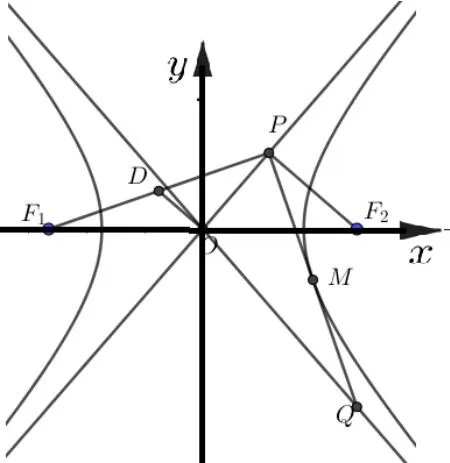
解取PF1的中点D,连接OD,则,所以OD⊥OP. 计算易得|PF2| =b,所以|OP| =a,|OD| =于是,计算可得由结论2.1 可知又解得b= 2,,所以该双曲线的方程为

例2已知双曲线x2-y2=4,O为坐标原点,点P为双曲线上任意一点,过点P作双曲线两条渐近线l1,l2的垂线,垂足分别为A,B,则∆OAB的面积为____.

解由结论2.3 可知, 则∆OAB的面积为, 其中a=2,即∆OAB的面积为1.

例3已知双曲线O为坐标原点,点P为双曲线C1上任意一点,过点P作双曲线C2的两条切线,切点分别为A,B,直线AB与C1的两条渐近线交于D,E两点,则∆ODE的面积为____.

解由结论2.6 可知∆ODE的面积为λ2ab, 其中λ=4,a=1,,代入计算得∆ODE的面积为