一个求解二维非线性时间分数阶波动方程的向后欧拉差分格式*

张光辉

(宿州学院数学与统计学院,安徽 宿州 234000)

0 引言

由于能有效地描述物理、化学和控制工程等领域的许多现象,近几十年来分数阶常微分和偏微分方程在以上领域引起了广泛的关注[1]。分数阶偏微分方程是古典偏微分方程的推广,研究者发现含有分数阶的微分方程可以更加准确地来描述诸多领域中的自然现象[2-4],如时间和空间分数阶扩散方程能够解释反常扩散和复杂系统的传送动力学。对于分数阶模型中的分数阶扩散-波动方程解析解的求解非常困难,主要研究集中于数值解法的讨论[5-8],但由于数值算法的研究起步相对较晚,求解多维非线性时间分数阶微分方程的算法设计和理论都是一个难点.本文主要研究求解时间分数阶非线性二维波动方程的数值方法.

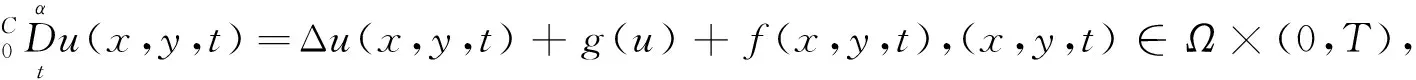
u(x,y,t) = 0,(x,y,t)∈∂Ω×(0,T),

(1)

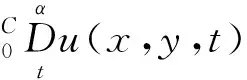
Δ为二维Laplace算子,Ω=(0,L1)×(0,L2),∂Ω为其边界.g(u)为满足Lipschtiz条件的非线性光滑函数,且g(0)=0.在式(1)中,如果u(x,y,0)=φ(x,y)≠0,ut(x,y,0)=ψ(x,y)≠0,则可由变换u(x,y,t)-φ(x,y)-tψ(x,y)将非齐次条件齐次化．

1 预备知识

引理1[9]式(1)和下面的式(2)等价．

u(x,y,t) = 0,(x,y,t)∈∂Ω×(0,T),

(2)

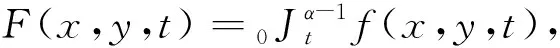
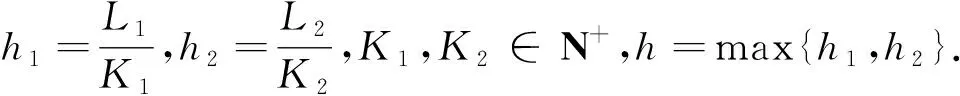
在时间方向上,设:

Tτ={tn|tn=nτ,n=0,1,2,…,M}.

定义网格函数空间:

引入以下差分算子:

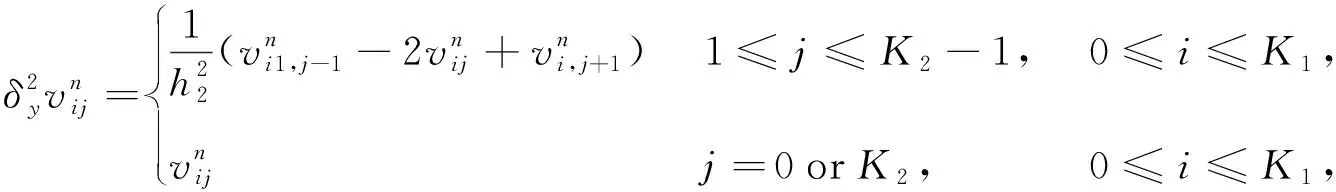
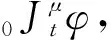
(3)

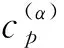
(4)

引理2[10]如果φ(t)是关于t的实值连续可微函数,φt(t)∈C1([0,T]),则式(3)的积分误差有如下估计式:

(5)

其中tn∈[0,T],常数C不依赖于τ.

(6)

(7)

为叙述方便,记:

(8)

(9)

(10)

对任意的1≤i≤K1,1≤j≤K2,1≤n≤M成立,其中常数C不依赖于h1,h2,τ.

2 向后欧拉差分格式的建立

在(xi,yj,tn)(1≤i≤K1-1,1≤j≤K2-1,0≤n≤M-1)处考虑式(2),有:

(11)

由引理4可知

(12)

(13)

另外,记

(14)

(15)

将式(12)～(15)代入式(11),得对任意的1≤i≤K1-1,1≤j≤K2-1,0≤n≤M-1,

(16)

其中:

由引理2和引理4得,对任意的1≤i≤K1-1,1≤j≤K2-1,0≤n≤M-1,

(17)

(18)

(19)

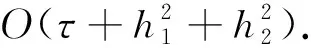
3 数值算例

例1 考虑如下的时间分数阶非线性波动方程

(20)

设式(20)具有式(1)所要求的齐次初边值条件,其中右端源像

其中g(u)=u3.易知式(20)具有解析解u(x,y,t)=t2+αsin(πx)sin(πy).

先将式(20)转化为等价的分数阶积分-微分方程式

(21)

对于式(21),取T=1,h=h1=h2=0.001,分别取不同α,τ,用式(18)～(19)计算当t=tM=1时所得数值解的误差和时间方向的收敛阶．计算结果见表1．

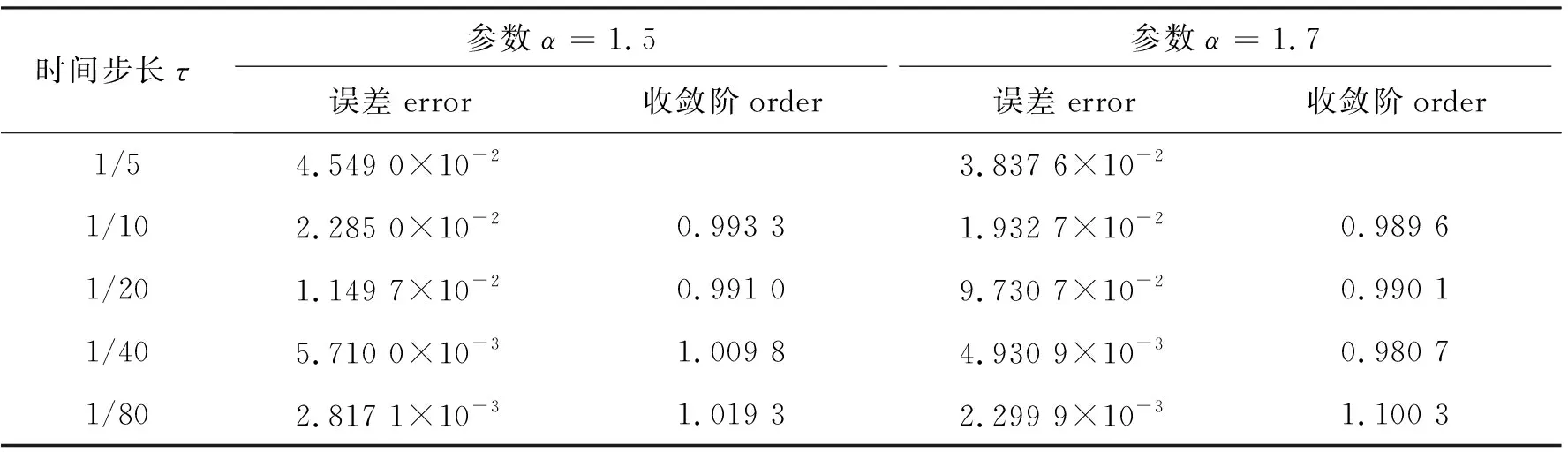
表1 固定h=0.001时,式(18)～(19)在时间方向的误差和收敛阶

取T=1,τ=0.001,分别取不同α,h,用式(18)～(19)计算当t=TM=1时所得数值解的误差和空间方向的收敛阶．计算结果见表2．

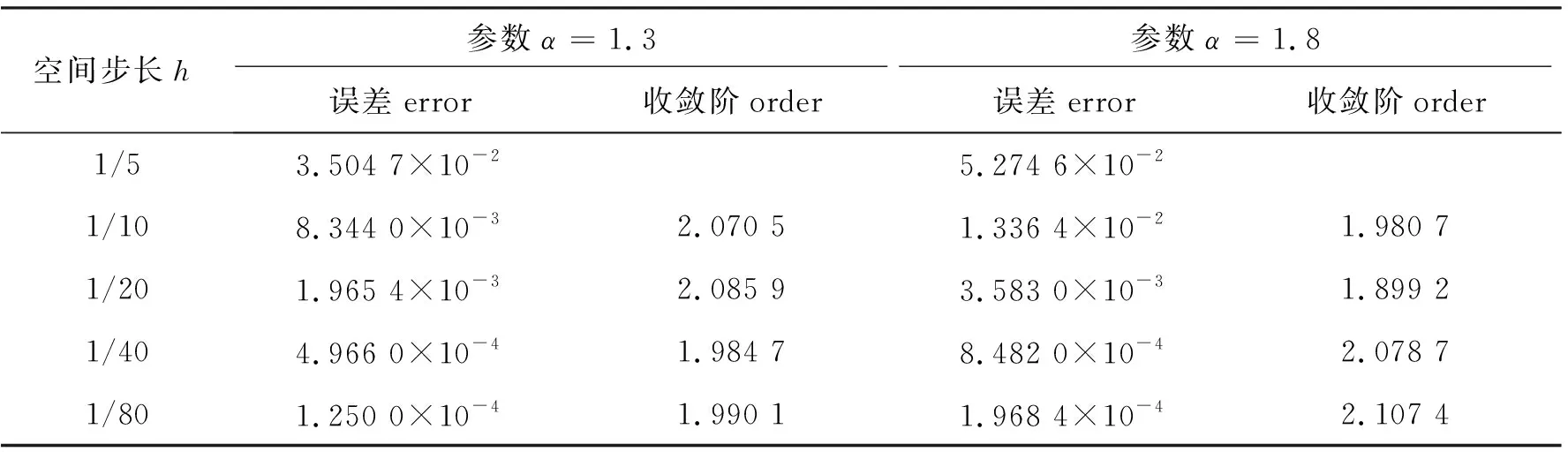
表2 固定τ=0.001时,式(18)～(19)在空间方向的误差和收敛阶

4 结束语