车用双相高强钢的动态力学性能及本构模型的对比
2023-11-27郑崇嵩侯聚英孟宪明程从前
徐 莉,郑崇嵩,侯聚英,吴 昊,张 赛,孟宪明,高 猛,程从前
(1.江铃汽车股份有限公司,南昌 330100;2.中汽研(天津)汽车工程研究院有限公司,天津 300300;3.大连理工大学材料科学与工程学院,大连 116024)
0 引 言
为适应低碳化、信息化、智能化的汽车技术发展趋势,先进高强钢与热成形钢在汽车车身中的应用量一直稳步增长[1]。双相高强钢作为先进高强钢的一种,具有强度高、强屈比大和塑性良好等优点,是汽车结构件主要用材之一[2-4]。汽车碰撞仿真是汽车设计研发的重要环节,相关材料性能参数的准确性决定碰撞仿真精度,是直接影响汽车设计验证和后续实车碰撞试验的关键因素之一。汽车碰撞过程是一个瞬时动态过程,车身材料在碰撞时的应变速率可达500 s-1,甚至更高[5]。因此,如何建立精度较高的双相高强钢动态力学性能本构模型,使其既能满足仿真需求,又能准确反映材料的动态力学性能,成为车用双相高强钢研发应用中的关键。
目前,国内外学者对汽车材料动态力学性能的本构模型进行了大量研究。张伟等[6]采用引入应变速率强化项的Swift-Hockett/Sherby模型对HC440/780DPD+Z钢的本构模型参数进行了拟合,拟合相关度系数达到0.98,高于应变速率敏感性指数非线性的Johnson-Cook修正模型。张赛等[7]使用应变速率的函数表达式对Johnson-Cook模型(简称JC模型)中的应变速率敏感系数进行修正,采用修正的JC模型对B250P1钢的本构模型参数进行拟合,修正后的拟合曲线与试验曲线的相对误差在8%以内。邓云飞等[8]采用修正的JC模型描述了6061-T651铝合金在大应变、高应变速率和高温下的流动应力行为。LI等[9]采用修正的JC模型和Zerilli-Armstrong (ZA)模型描述了DP780双相钢的动态力学性能,发现修正的ZA模型的精度更高。可知,采用传统JC本构模型描述材料动态力学性能时存在拟合精度偏低的不足,针对具体材料建立合适的本构模型是汽车材料动态力学性能研究的主要趋势。除提升模型拟合精度外,如何减少模型参数数量,兼顾仿真精度和计算速率,是本构模型在碰撞仿真应用的重要研究方向。因此,有必要对多种模型进行对比研究。然而目前的研究主要局限于1种模型或2种模型在单一材料中的对比,而对采用多种本构模型所得不同材料拟合结果的分析鲜有报道。为此,作者以2种双相高强钢HC340/590DP、HC700/980DP为研究对象,通过不同应变速率(0.001~500 s-1)下的室温拉伸试验,研究了2种钢的动态拉伸性能;采用JC模型、Swift-Hockett/Sherby模型以及将Swift-Hockett/Sherby模型引入到Ludwik模型中的修正模型对流动应力-应变曲线进行拟合,并与试验结果进行对比,分析了3种模型的拟合精度,以期为汽车结构设计中的工程应用提供试验参考。
1 试样制备与试验方法
试验材料选用牌号分别为HC340/590DP、HC700/980DP且厚度均为1.2 mm的双相高强冷轧钢板(市售)。根据GB/T 30069.2-2016,采用电火花切割方法加工出如图1所示的准静态拉伸试样和动态拉伸试样,试样长度方向与钢板轧制方向一致。
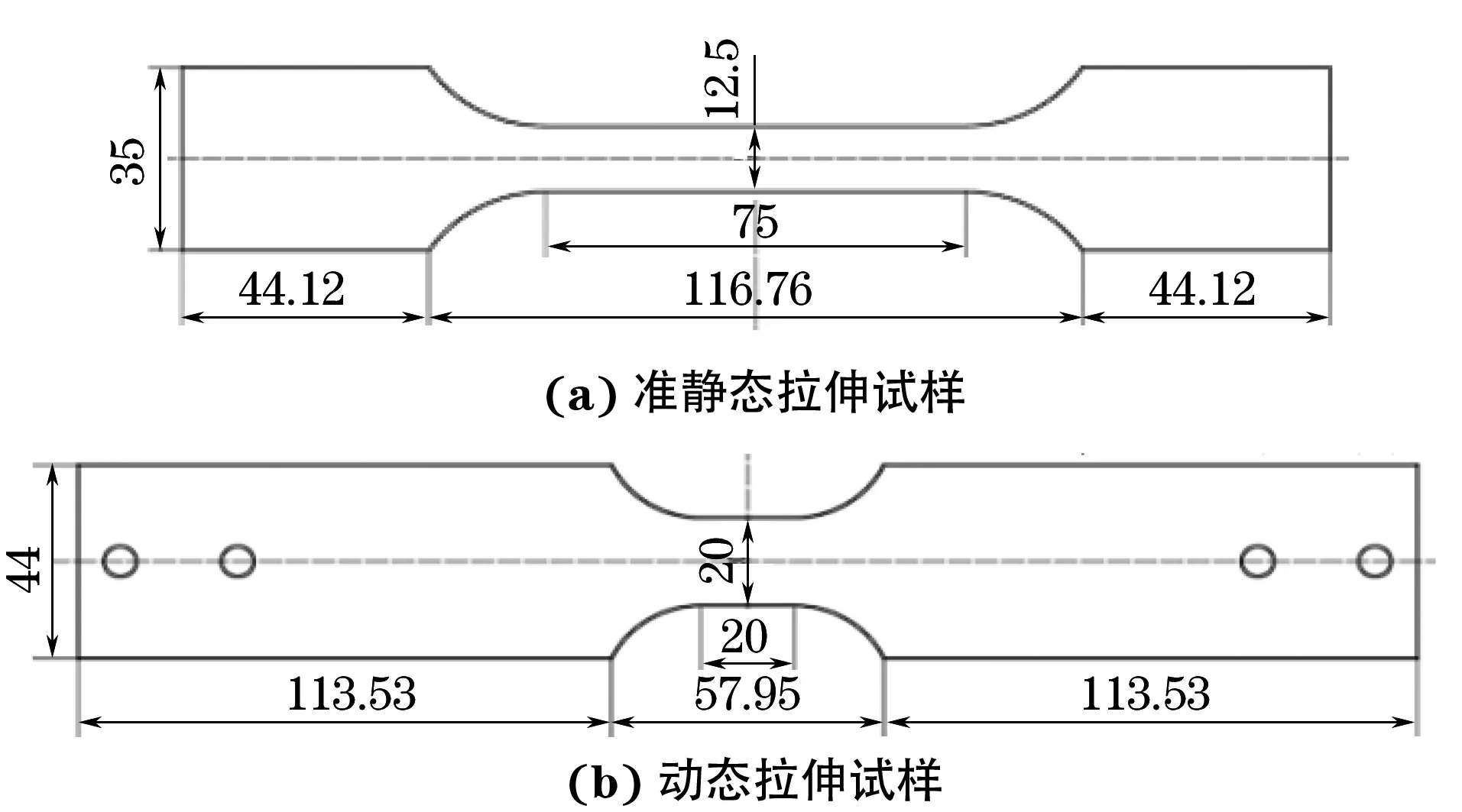
图1 准静态拉伸试样和动态拉伸试样的尺寸Fig.1 Dimension of quasi-static tensile sample (a) and dynamic tensile sample (b)
按照GB/T 228.1-2010参考方法A,采用CMT5205型电子万能试验机进行准静态拉伸试验,应变速率为0.001 s-1,试样标距为50 mm。按照GB/T 30069.2-2016,在Zwick Roell HTM16020型液压伺服式动态拉伸试验机上进行动态拉伸试验,应变速率为0.1,1,10,100,500 s-1,同一应变速率下进行3次以上试验,试验结束后采用GOM Correlate Professional 2020软件对数据进行处理,得到应力-应变曲线。
2 试验结果与讨论
由图2可见,2种试验钢的应力-应变曲线均经历了弹性、屈服、强化、颈缩4个阶段。随着应变速率的增大,2种试验钢在塑性变形阶段同一应变下的流动应力增大。由图3可以看出:与0.001 s-1应变速率下相比,试验钢在高应变速率下的屈服强度和抗拉强度明显升高,这表明2种试验钢都具有应变速率强化效应。在高应变速率下,2种试验钢的断后伸长率明显增加,但最大力总延伸率变化不明显。不同应变速率下HC700/980DP钢的强度均高于HC340/590DP钢,但这2种试验钢的强度均随应变速率的增加呈幂增长趋势。2种试验钢在高应变速率下均呈现出增强增塑的现象,这与加工硬化和动态回复相关[10-11]。应变速率的增大促进了位错增殖,位错密度增大后位错间缠结导致位错运动阻力增大,产生应变硬化效应,导致屈服强度和抗拉强度增大。此外,在高应变速率下,位错运动阻力大,变形速率快,材料中出现绝热升温现象,产生热软化作用[12];热软化作用及其动态回复有利于降低位错运动阻力,从而提高材料的塑性。随着应变速率的增加,2种试验钢的强度提高系数增大,但强屈比降低,表明应变硬化效应随应变速率的增加而增大,同时热软化和动态回复效应随应变速率的增加变得更加明显。
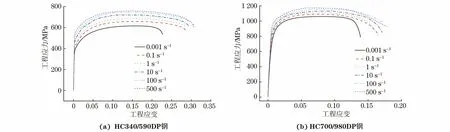
图2 不同应变速率下HC340/590DP钢和HC700/980DP钢的工程应力-工程应变曲线Fig.2 Engineering stress-engineering strain curves at various strain rates of HC340/590DP steel (a) and HC700/980DP steel (b)

图3 试验钢的拉伸性能参数随应变速率的变化曲线Fig.3 Tensile property parameter vs strain rate curves of test steel: (a) elongation; (b) strength; (c) strength increment coefficient and (d) strength yield ratio
3 动态力学性能本构模型的对比
3.1 Johnson-Cook模型拟合结果
流动应力模型是指流动应力σ与真应变ε的关系模型,通常采用的流动应力模型有Ludwik模型、JC模型、Swift-Hockett/Sherby模型等[13-15]。JC模型由Johnson和Cook于1983年提出,能够充分描述应变速率和温度对材料流变行为的影响。该模型形式简单、使用方便,模型中的变量计算方便,在一般的冲击动力学研究中得到广泛的应用[16-17]。JC模型中流动应力对应变速率与温度的依赖关系[18]可表示为
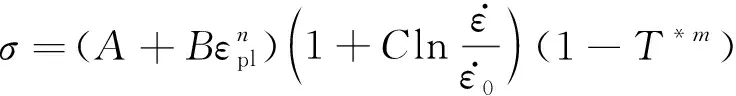
(1)
T*=(T-Tr)/(Tm-Tr)
(2)

由于试验中不考虑温度对材料动态力学性能的影响,因此可将JC本构模型简化为
(3)
用简化的JC模型对HC340/590DP钢和HC700/980DP钢的应力-应变曲线进行拟合,不同应变速率下仅需拟合4个参数,拟合过程简单,拟合曲线如图4所示,拟合参数如表1所示。由图4可知,JC模型拟合得到的应力-应变曲线与试验结果之间存在一定偏差,特别在应变较大的区域,JC模型拟合应力偏高,且偏高的程度随应变速率的增加而明显增大。拟合应力偏高会导致在动态力学性能模拟过程中的安全裕度过大。在JC模型待定系数确定以后,采用应变速率内插法可以得到不同应变速率下的拟合曲线,通过这种方式可以在已知试验范围内对未进行测试的应变速率下的流动应力-应变曲线进行预测。

表1 HC340/590DP钢和HC700/980DP钢的JC模型拟合参数值
3.2 Swift-Hockett/Sherby模型拟合结果
Swift-Hockett/Sherby模型简称SHS模型,由Swift硬化模型与Hockett/Sherby硬化模型加权组合而成,适用于描述金属材料在不同应变速率下的流动应力-应变曲线[18]。Swift模型属于非饱和模型,Hockett/Sherby模型属于饱和模型,将2个模型引入加权系数进行组合[20-21],得到
σ=(1-α)[c(εpl+ε0)t]+
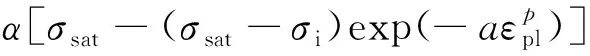
(4)
式中:α为加权系数;ε0为屈服点处的应变;σi为初始屈服应力;σsat为饱和应力;a,t,c,p均为材料常数。
用SHS模型对2种试验钢的流动应力-应变曲线进行拟合,拟合曲线如图5所示,拟合参数见表2。由图5可知,SHS模型拟合的流动应力-应变曲线与试验结果基本一致,可见该模型能准确地描述2种试验钢在不同应变速率下的屈服应力以及应变速率强化效应。与JC模型拟合结果相比,该模型的拟合精度更高,但是需要单独对不同应变速率下SHS模型中的8个参数进行拟合。这一方面导致拟合过程复杂,计算量增大,另一方面因各拟合参数与应变速率间应力没有耦合性,不能通过应变速率内插法对未知应变速率下的流动应力-应变曲线进行预测。
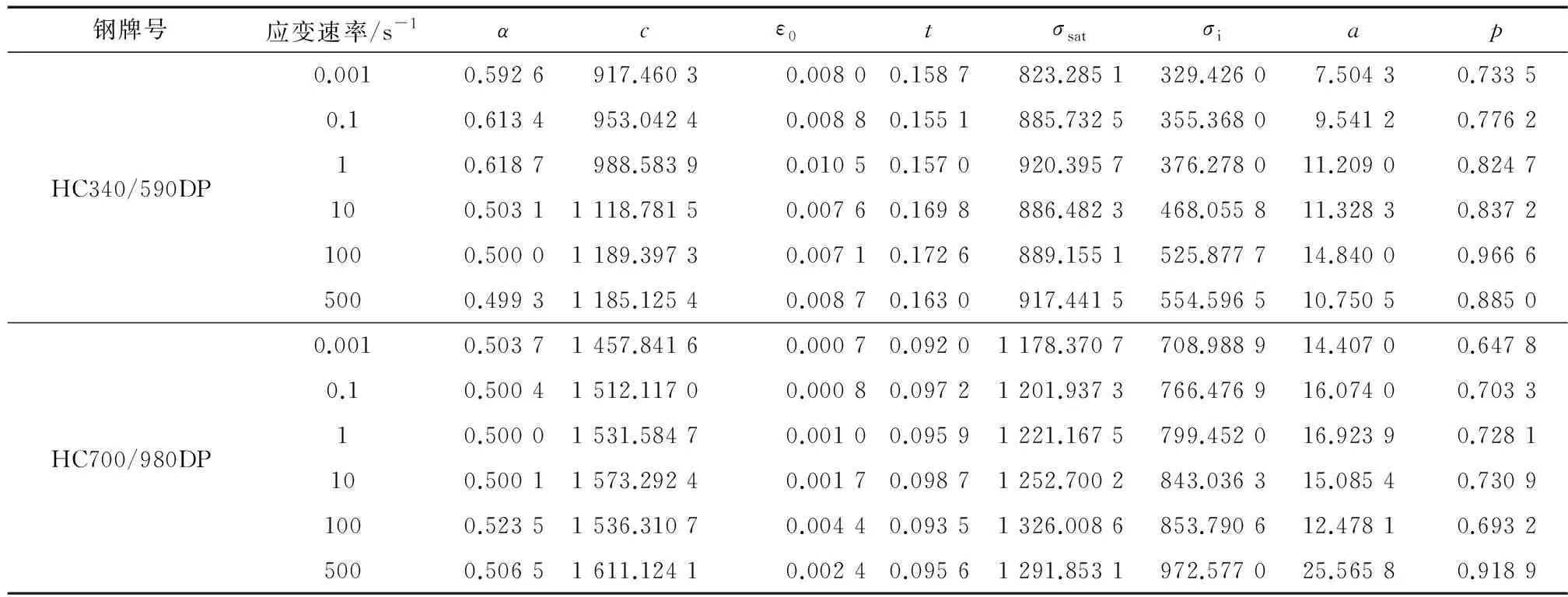
表2 HC340/590DP钢和HC700/980DP钢的SHS模型拟合参数值
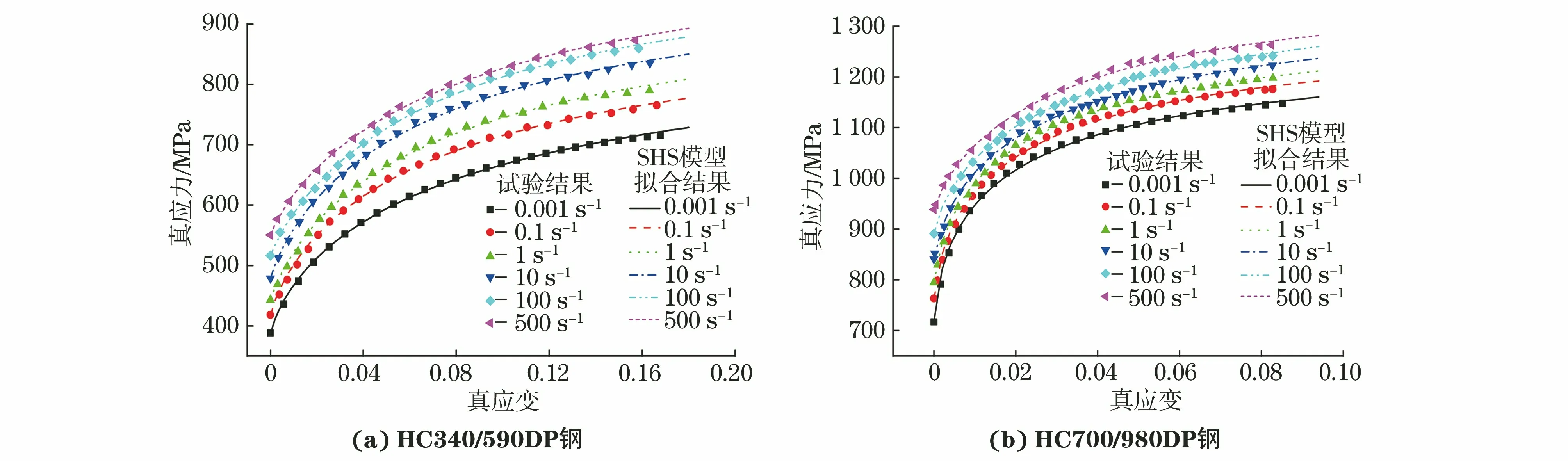
图5 SHS模型拟合得到HC340/590DP钢和HC700/980DP钢的真应力-真应变曲线与试验结果的对比Fig.5 Comparison between true stress-trure strain curves fitted by SHS model and test results of HC340/590DP steel (a) and HC700/980DP steel (b)
3.3 修正的Ludwik模型拟合结果
Ludwik模型是Ludwik在1909年提出的经验模型。为了解决SHS模型中各应变速率间的应力与拟合参数的非耦合性以及无法采用应变速率内插法进行预测的问题,并结合应力随着应变的增长呈幂增长趋势的试验结果,作者将Swift-Hockett/Sherby模型引入到Ludwik模型中对Ludwik模型进行修正,具体表达式为

(5)
σ=σs+K[(σ0-σs0)÷100]n
(6)
σ0=(1-α)[c(εpl+ε0)t]+
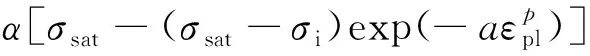
(7)
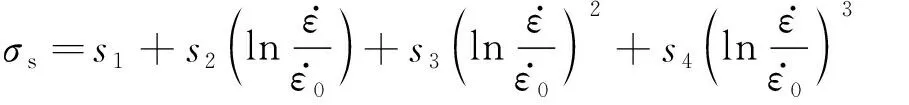
(8)
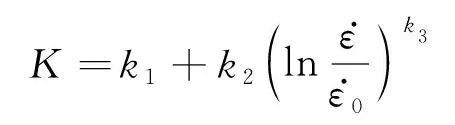
(9)
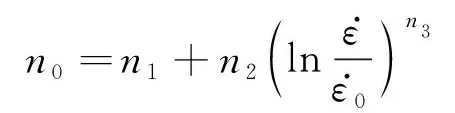
(10)
式中:σs为屈服强度;σ0为初始应变速率下的流动应力;σs0为参考应变速率下的屈服强度;K,n0,k1,k2,k3,n1,n2,n3,s1,s2,s3,s4均为材料常数。
用修正的Ludwik模型对2种试验钢的流动应力-应变曲线进行拟合,拟合曲线如图6所示,拟合参数见表3。由图6可知,修正的Ludwik模型拟合得到的不同应变速率下的流动应力-应变曲线与试验结果相吻合,且在低应变速率和高应变速率时均保持稳定。在拟合结果中各应变速率间的应力具有相关性,需拟合参数较少。该模型可以较好地描述2种试验钢在不同应变速率下的流动应力-应变曲线。

表3 HC340/590DP钢和HC700/980DP钢的修正Ludwik模型拟合参数值
3.4 不同模型的拟合度对比
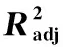
表4 各模型模拟不同试验钢在不同应变速率下真应力-真应变曲线的
4 结 论
(1) 随着应变速率的增大,HC340/590DP钢和HC700/980DP钢的屈服强度、抗拉强度和断后伸长率均有一定程度的提升,强度提高系数增大,强屈比降低,表现出增强增塑的现象。
(2) JC模型的拟合度较低,平均值为0.950,需拟合的模型参数最少;SHS模型的拟合度最高,平均值为0.999,需拟合的模型参数最多,不能通过应变速率内插法对未知应变速率下的流动应力-应变曲线进行预测;修正的Ludwik模型的拟合度平均值为0.997,略低于SHS模型,需拟合的模型参数较少。
(3) 修正的Ludwik模型既保留了各应变速率间应力具有耦合性的特点,又保持了高拟合精度,可以准确地描述2种钢在高应变速率下的动态流变行为。
