不同参数对交叉簧片型柔性铰链刚度特性的影响*

2023-11-27左皓琛

机电工程 2023年11期

关键词：簧片铰链交叉

左皓琛,梁松*,闫明

(1.沈阳工业大学机械工程学院,辽宁沈阳 110870;2.辽宁省冲击防护与损伤评估技术工程研究中心,辽宁沈阳 110870)

0 引言

柔性铰链是柔性构件的一个分支,其利用材料的柔性变形来传递力、位移和能量,可以消除侧隙、摩擦和磨损,具有结构简单、质量小等优点,在精密传动和控制领域有着广泛的应用。

将柔性铰链的优点应用在隔振系统中,亦有更优的隔振效果。而柔性铰链的刚度对隔振系统性能有重要影响,刚度与柔性铰链的本身参数和所受载荷紧密联系。由此可见,柔性铰链的刚度特性对柔性铰链的结构设计至关重要。

而要研究柔性铰链一般都会从柔性梁入手。

YIN X等人[1]运用欧拉伯努利梁理论对柔性梁的大变形进行了分析,并采用数值法和封闭法对其进行了求解与验证。交叉簧片型柔性铰链的变形最早由WITTRICK W H等人[2-3]进行了理论分析,假设其为线性小变形(旋转角度小于±5°),进而求得了载荷与旋转角度的关系。HARINGX J等人[4]同样对该类柔性铰链进行了研究,并假设其为对称变形,在此基础上得到了弯矩与变形的关系。GONÇALVES JUNIOR L A等人[5-7]采用迭代法和非线性有限元法,得到了柔性铰链的刚度特性;但在该研究中,研究者对大变形的情况考虑较少。LIU L等人[8]采用了仿真与实验的方法,对多簧片交叉型铰链进行了研究,对其轴向和径向刚度分别进行了分析与计算。BI S等人[9-11]采用近似和仿真的方法,对交叉簧片型柔性铰链的刚度特性进行了研究,得到了载荷与变形的关系;但其采用的方法只在较小变形范围内有效。李永振等人[12]采用理论近似方法对柔性铰链进行了分析,结果表明,只有在垂直载荷和旋转刚度较小时,交叉簧片型柔性铰链的刚度才能近似保持为常值,而再增大垂直载荷,转动刚度也会随之逐渐增大。杜绍扬[13]在针对柔性铰链的研究中,同样得出结论,即随着载荷的增加,该类柔性铰链旋转刚度不再是单一的常量;但他们对柔性铰链刚度特性分析得还不够全面。在实验测量柔性铰链刚度的方法上,文献[14-17]均基于几何光学理论,并搭载了柔性铰链的角位移变形测量平台;但在上述研究中,测量平台测量的工况范围有限。

目前的分析方法大多是针对线性小变形的柔性铰链刚度特性,且没有全面地考虑不同参数对柔性铰链刚度的影响。关于大变形柔性铰链的刚度分析方法的研究也尚不多见。

笔者以交叉簧片型柔性铰链为研究对象,从欧拉伯努利梁理论出发,建立大变形柔性铰链的力学模型,探讨不同载荷和几何参数对刚度的影响规律;给出模型求解方法,采用三维有限元分析模型,建立柔性铰链刚度测量实验装置,以探究不同参数对柔性铰链刚度特性的影响规律。

1 理论变形分析

1.1 铰链受载分析

交叉簧片型柔性铰链示意图如图1所示。

图1 交叉簧片型柔性铰链示意图

图1中,交叉簧片型柔性铰链主要包括固定端、簧片和移动端。

其中,图1(a)表示了簧片的参数,包括长度L、宽度B和厚度T。

图1(b)为几何参数和变形图,包括2根簧片的交叉位置λL(λ∈(0,1))和交叉角度2α(α∈[30°,60°])。当柔性铰链移动端底部中间受垂直力P、水平力F和弯矩M时,将会产生一个旋转角度θ。

交叉簧片型柔性铰链的受载分析模型如图2所示。

图2 交叉簧片型柔性铰链受载分析模型

当移动端底部受到载荷时,两根梁均会产生变形。为了方便分析,笔者将移动端B1B2的中点所受到的P、F和M这3种载荷分别转换到两根梁A1B1和A2B2上,这样就使柔性铰链整体受到的载荷转换到了每根梁上,每根梁所受的力为轴向力Pi、垂直力Fi和弯矩Mi(i=1,2代表梁1和梁2),力的方向以变形前局部坐标系xAiy为基准。

由于考虑了x和y方向的位移,因此,该研究为柔性铰链的大变形分析。

1.2 铰链变形分析

柔性梁的变形计算以欧拉伯努利梁为主,即梁在变形后,总有一个截面的长度保持不变,如图3所示。

图3 柔性梁变形分析

设梁的总长度为L,任意一点位移(x,y)弧长为s,该点处的切向角度为ψ;设梁的端点C处所受轴向力为Pi、垂直力为Fi、弯矩为Mi,则根据曲率的变形关系,任意一点处的弯矩M为:

-Pi(ΔY-Y(X))+Fi(L-X)+Mi

(1)

式中:E为材料的弹性模量;I为截面惯性矩。

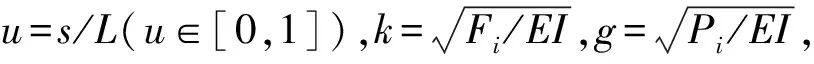
(2)

即可得到ψ与u的微分方程,其边值条件为u=0,ψ=0;u=1,dψ/du=LMC/EI,可用打靶法[18]求解该边值问题。

当解出ψ与u的对应关系后,可由下式获得直角坐标系下变形后的形态:

(3)

其中:u0由0到1变化,即可表示梁上任意一点(x,y)处的位移变化。

接着,笔者对柔性铰链的变形进行整体分析。

先对所有变量进行无量纲化处理:

(4)

式中:L为簧片的长度;EI为材料的抗弯刚度。

则根据力的平衡关系可列出以下方程:

f=(p2-p1)sinα+(f1+f2)cosα

(5)

p=(p1+p2)cosα+(f1-f2)sinα

(6)

m=[(p1-p2)cosα+(f1+f2)sinα]λsinαcosθ-

[(p1+p2)sinα-(f1-f2)cosα]λsinαsinθ+m1+m2

(7)

由于B1,B2两点的距离保持不变,可列出x和y两个方向的几何位移平衡式如下:

(δy1-δy2)cosα+(δx1+δx2)sinα=2λsinα(1-cosθ)

(8)

(δy1+δy2)sinα-(δx1-δx2)cosα=2λsinαsinθ

(9)

在式(5)～式(9)中,有11个变量,而只有5个方程,因此,需采用柔性梁变形模型。

笔者首先对式(1)进行无量纲转化,即:

初始条件为:

因此,可求得关于参数δyi和θ的方程如下:

δyi=yi(1),i=1,2

(10)

(11)

而δxi(i=1,2)的表达方式为:

(12)

笔者联立式(5)～式(9)和式(10)～式(12),可列出关于11个参数的非线性方程组,但该方程组没有封闭解,只能采用迭代法进行求解。

L-M法对该类方程有较好的解[19]。设F(x)是关于x的11维非线性方程组,其中,x为δxi,δyi,pi,fi,mi,θ(i=1,2)这11个变量,设定步长使该迭代具有二次收敛性,即可完成求解。

2 刚度特性分析

2.1 弯矩对旋转刚度的影响

接下来,笔者将从交叉簧片型柔性铰链的力学模型出发,开展柔性铰链的刚度特性分析,并讨论几何参数与载荷形式对刚度特性的影响。

一般定义刚度为载荷与旋转角度θ的比值,则旋转刚度KM、水平刚度KF和垂直刚度KP定义为:

(13)

其中:

(14)

式中:pi,fi,mi均为前述非线性方程组解的变量。

由式(13)和式(14)可知:交叉簧片型柔性铰链的刚度与材料的长度L、宽度B、厚度T、弹性模量E以及所受载荷M、F、P均有关。

其中,弯矩M与柔性铰链旋转刚度KM的关系如图4所示。

图4 弯矩M与柔性铰链旋转刚度KM的关系

图4中,考虑旋转刚度,笔者给出了只有弯矩载荷时弯矩M与旋转角度KM的关系,并将其与文献[9]中的分析结果相比较。

由图4可以看出:在弯矩较小时,柔性铰链的旋转刚度与文献[9]的结果相近,且近似为常数;但当弯矩足够大时,旋转刚度出现了非线性变化。

2.2 交叉系数和交叉角度对刚度的影响

几何参数交叉系数λ和交叉角度α对柔性铰链旋转刚度KM的影响,如图5所示。

由图5可知:交叉系数对柔性铰链旋转刚度影响很大,在交叉系数λ=0.5时,旋转刚度最小;当λ接近0或1时,旋转刚度达到最大。当λ由0.5减小到0或增加到1时,旋转刚度以非线性形式增大;且对于不同的交叉角度α,旋转刚度的曲线基本保持一致,即交叉角度对旋转刚度几乎没有影响。

因此,在考虑旋转刚度时,需注重几何参数交叉系数λ的影响。

2.3 垂直载荷和水平载荷对刚度的影响

考虑水平载荷和垂直载荷对旋转刚度的影响,在一定弯矩M下,不同水平载荷F和垂直载荷P对不同交叉系数λ下旋转刚度KM的影响,如图6所示。

图6 垂直载荷P和水平载荷F对柔性铰链旋转刚度的影响

由图6可以看出:水平载荷相对垂直载荷对柔性铰链的刚度影响更大,且交叉系数为0.5,比0.2时的影响更大,这同样证明了图5的分析结果。当水平载荷与弯矩使柔性铰链的变形方向相同时,随着水平载荷的增大,旋转刚度变化较小;当两者方向相反时,旋转刚度变化很大。

因此,笔者需优先考虑交叉系数λ与水平载荷F对旋转刚度KM的影响。

柔性铰链在垂直方向上的刚度远大于水平刚度和旋转刚度,因而垂直载荷对结构的变形位移影响较小,故以下笔者只讨论水平刚度及其受几何参数的影响。

柔性铰链的水平载荷F与水平刚度KF的关系如图7所示。

图7 水平载荷F与水平刚度KF的关系

在图7中,显示出了水平载荷F与水平刚度KF的关系与文献[9]中数据的对比。

由图7可以看出:相比于旋转刚度而言,水平刚度在载荷增大过程中,其近似保持为常值。文献[9]也证明了这一点。

图4和图7都表明,应更侧重于对旋转刚度的分析。

2.4 几何参数对水平刚度的影响

几何参数对水平刚度的影响如图8所示。

图8 几何参数λ,α对柔性铰链水平刚度KF的影响

由图8可以看出:水平刚度相对于交叉系数λ并不是对称分布的,当λ越靠近0,则水平刚度越大;当λ在0.4～0.9范围内,其刚度处于稳定状态;交叉角度α相对于λ对柔性铰链的水平刚度影响较小。

因此,在分析几何参数对其影响时,应首先考虑交叉系数λ。

3 有限元分析与刚度测量实验

笔者采用有限元法和实验测量法,分别对交叉簧片型柔性铰链的刚度特性进行分析,并将二者分析结果与理论分析结果进行比较。

由于这两种方法都对模型的具体参数和施加的载荷有要求,因此,笔者具体分析7种不同参数对柔性铰链的刚度特性的影响。

3.1 有限元分析

7种不同参数均受到相同的弯矩载荷,其中簧片的材料为65 Mn弹簧钢,弹性模量为200 GPa,泊松比μ=0.3,长度L=60 mm,宽度B=10 mm,厚度T=0.5 mm。

具体参数如表1所示。

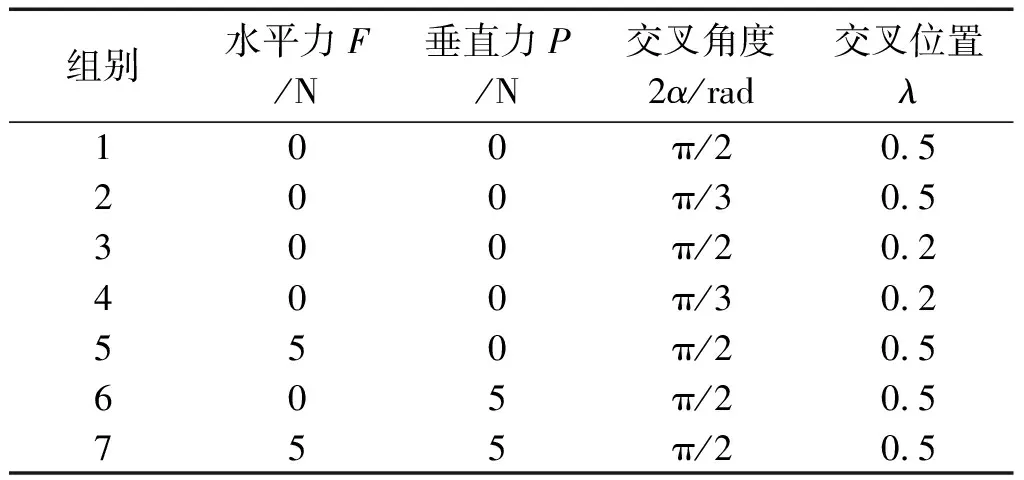
表1 不同参数下的交叉簧片型柔性铰链

表1中,1～4组的交叉系数和交叉角度不同,5～7组施加的载荷不同。

表1中,第1组几何参数下柔性铰链的有限元模型,如图9所示。

为了与实验模型相对应,柔性铰链的边界条件为在固定端施加完全约束,在移动端底部中心偏下一定距离施加载荷。为防止产生扭转,笔者将簧片设为对称型[20-21]。

由于簧片的厚度远小于长度和宽度,且只产生弯曲变形,因此,笔者对簧片采用一阶线性非协调单元划分网格,厚度方向为两个网格;其他地方采用一阶缩减单元网格划分。

为减少计算时间,且不影响分析结果,其上下两端约束为刚体,模型均采用六面体网格。

3.2 刚度测量实验

此外,笔者开展了刚度特性的实验测量方法研究,设计并搭载了柔性铰链刚度测量实验平台。

测量平台的功能模块如图10所示。

图10 柔性铰链刚度测量实验平台功能模块图

该平台主要包括了4种模块,即支撑、夹持、加载和测量模块。它们的功能分别为:1)保证系统有足够的平衡稳定性;2)保持柔性铰链的交叉系数和交叉角度与工况相对应;3)能任意加载水平、垂直和弯矩3种载荷;4)可以测量柔性铰链受载后产生的旋转角度。

柔性铰链刚度测量平台的整体装置如图11所示。

图11 柔性铰链刚度测量平台

图11中,柔性铰链上端固定在铝型材上,下端使用轴承座固定了一个承载轴;弯矩M、水平载荷F和垂直载荷P可以由承载轴传给柔性铰链,利用悬挂在周围的砝码施加载荷,增加或减小砝码的重量可以调整载荷的大小。

其中,水平和垂直载荷与砝码重量相同,弯矩大小为砝码的重力与相应力臂的乘积。

笔者根据几何光学理论的旋转角度测试方法[14],对柔性铰链的变形角度θ进行测量。在初始状态时,激光会通过反射镜在标定靶上确定一个位置。当柔性铰链受载后会产生偏转,位于铰链底端的平面镜会发生转动,进而改变激光的原有路线,使其偏离原有的标记靶位置;当旋转调整镜的角度使激光标记点恢复到原有位置时,调整的角度即为柔性铰链的旋转角度θ,计算载荷与旋转角度的比值即为柔性铰链的刚度。

柔性铰链装置的三维设计图与实物图如图12所示。

柔性铰链主要由簧片、夹片、滑动块和固定装置组成。其中,更改滑动块的位置可以改变柔性铰链交叉系数λ的大小,更改与簧片紧贴的滑动块斜面角度即可调整交叉角度α的大小,即保证与表1中不同的几何参数相对应。

根据表1的前4组数据,笔者分别采用理论方法、有限元方法和实验测量方法,对柔性铰链的刚度进行计算。

对其给定相同的弯矩M,笔者分别计算了理论方法与有限元和实验测法的误差:

(15)

不同参数交叉簧片型柔性铰链旋转刚度如表2所示。