基于卡尔曼滤波与子带选取的轴承声信号增强方法*

杨小权,刘曰木,刘 江

(国能榆林能源有限责任公司,陕西 榆林 719000)

0 引 言

随着“中国制造2025”以及“智慧矿山”等战略的提出,我国煤炭行业面临着稳定高速发展机遇,同时其也对煤炭行业各关键设备的安全、稳定运行提出了新要求[1]。

皮带输送机是洗煤厂中的主要输送设备。其中,轴承是皮带输送机齿轮箱的重要组成部分,也是齿轮箱中较易损坏的零件之一[2]。现阶段,我国对于皮带机齿轮箱的监测主要采用人工巡查,听取有无异常噪声的方式,这对测量人员要求较高,且评判标准因人而异,检维修效率较低[3]。

基于声信号测量分析进行设备故障诊断的分析方法,被称为声学诊断技术(acoustical-based diagnosis,ABD)。相比于振动、温度等接触式测量方式,其具有传感器安装方便、采集信息量大等优势,可以大幅提高设备监测和故障诊断效率[4]。

然而皮带机齿轮箱声信号来源广泛,轴承信号受混响噪声及环境噪声的干扰大,极大地限制了声学诊断技术在皮带输送机故障诊断领域的应用。

目前,国内外学者均已开展了针对轴承声信号增强技术方面研究。AMARNATH M[5]提出了一种将经验模态分解(empirical mode decomposition,EMD)应用于轴承故障诊断的声信号处理方法,该方法可以分离轴承和齿轮的信号;但该方法并未针对轴承声信号各组成成分特点对EMD算法进行改进,导致其故障特征提取效果一般。鲁文波等人[6]采用近场声全息技术,对滚动轴承故障诊断声场分布特征进行了提取,该方法在近场中有较好的效果,但在工程应用多为远场测量的条件下,诊断精度较低。ZHANG D[7]提出了一种结合ISVD与RSSD算法的轴承噪声消除方法,该方法降低了谐波成分对轴承声信号的影响;但该方法未能消除混响效应对信号的影响,导致其在室内测量环境下低频干扰严重。YU G等人[8]采用递归最小二乘法(recursive least square,RLS)对轴承声信号进行了处理,其在声场稳定的环境中效果较好;但该方法需依赖仿真信号以减少混响噪声对目标信号的干扰,导致其自适应性一般。WU P等人[9]提出了一种将加权预测误差算法(weighted prediction error,WPE)与线性约束最小方差(linearly constrained minimum variance,LCMV)相结合的轴承声信号去混响方法,显著提高了信号的包络谐噪比;但该方法仅适用于多通道信号处理,在单通道场景下无法获得有效应用。

综上所述,现有轴承声信号增强方法受混响噪声及背景噪声干扰严重,导致室内测量条件下信号增强效果一般。

卡尔曼滤波是一种利用线性系统方程,基于系统输入输出观测数据,对系统状态进行最优估计的自适应滤波器,语音信号处理领域常使用卡尔曼滤波去除晚期混响噪声的干扰[10-11]。

齐园蕾[12]采用简化卡尔曼滤波消除了远场条件下的混响噪声,在降低算法复杂性的同时,保证了语音信号的质量。梅铁民[13]提出了一种卡尔曼滤波和反幂法相结合的自适应语音去混响方法,提高了语音信号的感知质量,在语音领域使用卡尔曼滤波消除混响具有较好的效果;但该方法的超参数需要人为设定。

工业生产中声场环境复杂,人为设定参数方式会降低信号增强效果和特征提取的准确率。

小波包分解常用于旋转机械振动信号的降噪分析,且已取得了较好的应用效果。

栾孝驰等人[14]将小波包与完全自适应噪声集合经验模态分解相结合,减少了环境噪声对轴承信号的影响。黄华等人[15]提出了一种基于小波包与图论诊断的数控机床进给系统故障诊断方法,该方法有效提高了故障的定位精度。

综合以上分析,笔者从声信号产生机理及信号传递角度出发,研究声信号混响产生原因、信号传递路径及各干扰成分特点。

为减少混响及背景噪声对轴承信号的影响,笔者提出一种基于卡尔曼滤波与小波包子带选取的声信号处理方法,在狭小空间测量环境下,对皮带输送机齿轮箱的轴承声信号进行增强;最后,通过轴承故障模拟试验,对基于卡尔曼滤波与小波包子带选取的方法进行验证。

1 理论基础

1.1 混响与声信号衰减

直达声是从声源直接传播到麦克风的信号,该部分信号无反射。混响是指除直达声信号外各路反射波的叠加总和,其中与直达声到达间隔在50 ms内的反射声称为早期反射声,对信号可起到一定的增强效果;50 ms后到达的反射声为晚期反射声,是混响信号的主要成分。

当单次反射声信号的能量降低至原信号的百万分之一时,认为该反射声不存在影响,衰减的总时长为混响时间。

声波在空气中的衰减主要由于声波能量被空气吸收导致,其衰减模型如下[16]:

A=A0γ=Ae-αs

(1)

式中:A0为信号初始幅值;A为经过传输距离s后的信号幅值;γ为信号在空气中传输s距离下的信号衰减系数;α为空气吸声系数。

空气吸声系数的计算公式如下[17]:

(2)

式中:f为信号中心频率;T为环境温度;P0为标准压强;T0为参考温度,即293.15 K。

1.2 卡尔曼滤波

卡尔曼滤波采用对前一时刻预测值和当前时刻的观测值与预测误差,计算得到当前时刻的最优估计值,从而实现对下一状态的预测目的。

卡尔曼滤波可针对离散线性系统进行滤波处理,系统状态方程与观测方程可表示如下[18]:

(3)

式中:Xk与Xk-1为状态向量;Ωk-1为动态噪声;Δk为观测噪声;Lk为观测值向量;φk,k-1为状态转移矩阵;Γk,k-1为动态噪声系统;Bk为观测方程系数。

依据广义二乘原理,设定Ωk、Δk均为白噪声且互不相关,卡尔曼滤波的递推方程如下[19]:

(4)

对式(4)进行进一步修正,结果如下[20]:

(5)

1.3 小波包分析

小波包分析是小波理论在信号处理应用领域的又一重大发展,它在小波理论的基础上引入最优基准准则,是一种比小波分析更为精细的时频分析方法[21]。小波包分析可基于分析信号特点自适应选择频带,与信号频谱相匹配,提高时频分辨率[22]。

针对小波包系数进行阈值操作并重构,所得信号相比小波变换处理具有更佳去噪效果。根据多分辨率分析,在时间t下,小波包ω0(t)及ω1(t)与尺度函数Φ(t)、小波函数ψ(t)关系如下[23]:

(6)

小波包分解层数的合理选取是信号特征准确提取的关键,过多的分解层数将导致信号失真及计算量激增,分解层数过少则会影响信号去噪效果。

具体分解层数计算公式如下[24]:

(7)

式中:L为最大分解层数,在工程使用中一般选择为3～6层;Fs为采样频率;Fd为缺陷频率。

2 声信号组成与信号增强方法

2.1 声信号产生机理

轴承加工过程中必然存在一定量的加工误差,造成轴承表面存在轻微不平整等问题。轴承装配过程中,同样会不可避免地存在细微偏差。同时,受到润滑条件及材料特性等因素的影响,轴承在无故障时也会存在一定的振动,该部分振动产生的声信号主要以谐波形式存在。

在运行过程中,轴承自身刚度将随转速及载荷的变化而实时变化,且受到滚动体挤压的作用,内外圈均存在一定的弹性变形。这种由于轴承间隙、滚动体及滚道的非线性赫兹接触力及由轴承支撑刚度变化导致的变柔性振动称为vc振动,其振动幅值相对较小。

其频率值求取表示如下:

ωvc=[(ω×r)/(R+r)]×n

(8)

式中:ωvc为vc振动频率;ω为轴承转频;R为外圈半径;r为内圈半径;n为滚动体个数。

当轴承存在缺陷时,故障部位在旋转过程中会受到周期性冲击,进而激发部件的稳态振动,产生的噪声以声能形式向四周辐射出去。该声信号具有明显的冲击特征,且冲击频率与轴承故障位置直接相关,为最能体现轴承运行状态的“有效目标信号”。

笔者将皮带输送机齿轮箱轴承视为一个单自由度的弹簧-阻尼系统,冲击信号经轴承辐射后将引起一系列的高频衰减,故障轴承因缺陷产生的声信号H(t)可表示如下:

H(t)=y0×e(-2πg×fn×t)

(9)

式中:y0为故障脉冲信号位移常数;g为轴承阻尼系数;fn为轴承固有频率。

齿轮箱轴承运行过程中,因皮带机自身各部件周期性振动将产生一定的周期性噪声,此类噪声将通过复杂的传递路径,经皮带机齿轮箱调制后,最终被麦克风传感器采集。

皮带机各类振动均与输入轴转速相关。该类振动产生的噪声由多种频率信号相互叠加而成,均为周期性随机噪声。电磁噪声、空气动力性噪声、皮带运行噪声及人员噪声等环境声信号未经齿轮箱调制,可直接通过空气传播至声音传感器。此类噪声存在较大的随机性与偶然性,并不包含有效的周期性信息,其成分与白噪声相近。

2.2 信号组成及传递

基于上述分析,笔者以包含正常轴承及故障轴承各一个的齿轮箱产生的声信号为例,进行信号组成分析及传递。其中,声音传感器采集所得声信号y(t)由上述各类信号(在空气中传播,并受墙面多次反射)叠加而成。

其组成如图1所示。

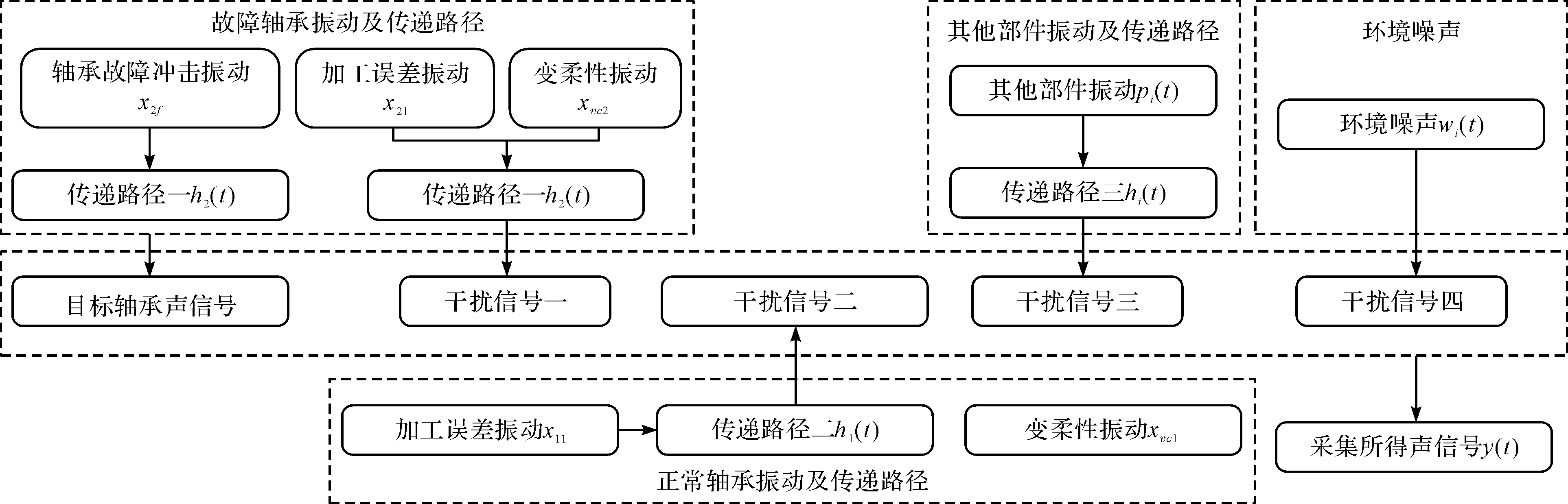
图1 轴箱轴承声信号传递路径及组成示意图

基于图1所示内容,其信号组成如下式:

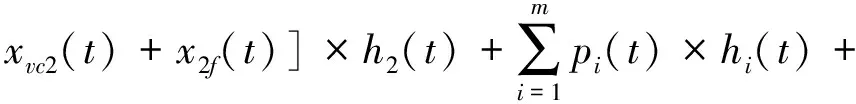
(10)

式中:ξ为反射面吸声系数;s为反射面间距;h(t)为各部件对应的声信号载波频率。

其中，为所选路径中的充电站个数。于是在电动汽车规划路径上的充电费用便能通过分时电价制定方式以及预测负荷表示。

由于皮带输送机齿轮箱轴承座固有频率较高,因此,轴承信号经高频调制后向外传播。

2.3 信号增强方法流程

综合上述声信号组成及传递路径分析可知,皮带机齿轮箱轴承声信号主要由具有冲击特性的故障声信号、皮带机其他部件振动产生的干扰信号以及各类信号反复叠加形成的混响信号组成。

受混响噪声与非故障部件振动干扰噪声的影响,传感器采集的声信号中轴承故障信号较为微弱,导致皮带机齿轮箱轴承声学诊断较为困难。因此,减少分析信号中的混响噪声及非故障噪声随机噪声的干扰,是准确挖掘隐藏在采集信号中轴承故障信息的关键。当待测轴承存在故障时,传感器采集所得信号必然与正常状态信号存在一定差异,通过比较待测信号与正常状态信号的差异提取故障信息,可以进一步降低背景噪声对故障信号的干扰。

针对待测信号的特点,卡尔曼滤波算法能够进行自适应逆滤波处理,减少因重复叠加导致的晚期混响信号对轴承故障信号的影响。

小波包降噪算法可以通过时频域分析,将信号分解为包含不同成分的子带信号,依据目标信号特点选取冲击成分占比最大的子带信号,从而实现轴承信号增强的目的。

综合以上分析,笔者提出采用卡尔曼滤波与小波包降噪相结合的方法,进行皮带机齿轮箱轴承诊断,其方法流程如图2所示。

图2 皮带机齿轮箱轴承声信号增强方法流程

2.3.1 去混响

笔者利用单个麦克风传感器分别采集皮带机齿轮箱轴承正常状态与待测状态下的声信号,并采用卡尔曼滤波,对正常状态及待测状态信号进行处理,完成信号去混响分析任务。

去混响过程伪代码如下:

输入:原始信号

输出:去混响后信号

1)ForJ← 0 to 0.75,step=0.25

2)ForD← 0 to 1,step=0.25

3)yJ,D=KalmanJ,D(x) #各参数组合卡尔曼滤波后信号

4)kJ,D=kurt(yJ,D) #计算峭度

5)End for

6)End for

7)Return最大峭度对应参数组合处理后的信号

2.3.2 子带选取

笔者选用db4小波作为基函数,并采用软阈值降噪方法对去混响后信号进行处理,对比待测状态与正常状态信号子带能量差异,确定最优子带。

由于轴承信号受传递路径高频调制的影响,其载波频率较高,一般设定采样频率为Fs=25 600 Hz,采样点数Fd=16 384。分解层数与采样频率和故障特征频率有关。当采样频率和故障特征频率确定后,结合式(7)可得到最大分解层数。考虑到轴承故障特征频率主要集中于1 kHz以下,故确定小波包分解层数为3层,将原始信号分为23=8个子带信号。

笔者分别计算正常与待测状态去混响后信号8个子带的能量值[E1,E2,…,E8]。

待测状态相比正常状态各子带信号能量的相对变化R计算公式如下:

(11)

式中:yt,yN为待测信号与正常状态信号波形幅值。

笔者对比了8个子带信号的能量相对变化值[R1,R2,…,R8]大小,选取变化最大的子带作为最优子带信号。

2.3.3 缺陷提取

笔者对最优子带信号进行包络谱分析以提取特征频率,对比实测特征频率与各故障的理论故障频率,完成对皮带机齿轮箱轴承的故障诊断。

3 试验验证

3.1 故障模拟试验

笔者设计并搭建了可模拟各类轴承故障的模拟试验台。其中,此处的轴承型号为NU205EM,其输入转速设定为1 200 r/min。

模拟试验台结构实物图如图3所示。

图3 轴承故障模拟试验台结构实物图

试验过程中,试验台靠近一侧墙面放置,声音传感器与试验台间的距离远小于室内两侧墙面间的距离。

试验具体设置如表1所示。

表1 试验参数设置表

笔者采用线切割加工的方式分别在不同轴承的外圈及内圈位置加工若干划痕模拟外圈与内圈故障,其缺陷形式如图4所示。

图4 轴承缺陷示意图

各组试验轴承故障信息如表2所示。

表2 轴承故障模拟试验基本信息表

3.2 方法验证

基于上述声信号衰减规律与声场条件,试验环境下混响时间为3.41 s,远大于50 ms,故属于混响声场。

笔者采用基于卡尔曼滤波与子带选取的方法对试验数据进行分析,并以故障程度较轻的外圈故障数据为例。

试验采集到的外圈故障原始声信号如图5所示。

图5 外圈故障原信号

笔者采用卡尔曼滤波对原信号进行处理。

不同卡尔曼增益J以及协方差D组合下的信号峭度分布,如图6所示。

图6 不同参数下卡尔曼滤波后信号峭度图

依据图6所示结果,笔者分别设定卡尔曼增益J=0、协方差D=1,依据上述参数组合对原信号进行卡尔曼滤波分析,所得信号波形及时频谱如图7所示。

图7 去混响后外圈故障信号

对比图5与图7发现:相比于原信号,去混响后信号幅值明显下降,且信号中的高频降低尤为显著,混响噪声消除效果显著。

笔者依据上述流程对去混响后信号进行三层小波包分解,并求取各子带能量值。

待测状态信号与正常状态信号各子带能量值相对比例,如图8所示。

图8 外圈故障与正常状态各子带信号能量占比

由图8能量对比可看出:相比正常状态,外圈故障信号第5子带的能量变化远大于其他子带,其能量相对变化R=4 000.26%。

因此,笔者选定该子带为最优子带,其信号波形及包络谱如图9所示。

图9 外圈故障最优子带信号

对比图7(a)与图9(a)发现:最优子带信号的波形幅值相比去混响后信号幅值更低,信号中的冲击成分更为明显;图9(b)中存在与外圈理论故障频率104.75 Hz相近的110.94 Hz成分f及其二到四阶的谐波分量,同时还存在与故障特征频率f、转频f0相关的频率成分,据此可以判断该轴承存在外圈故障。

笔者将上述方法与文献[7]所述ISVD-RSSD方法进行分析比较,验证基于卡尔曼滤波与子带选取的方法对于轴承故障提取的有效性。

通过对外圈原始信号进行分析,其降噪后信号波形及包络谱如图10所示。

图10 ISVD-RSSD方法降噪后信号

对比图9与图10发现:相比基于卡尔曼滤波与子带选取的方法,采用ISVD-RSSD方法降噪后所得信号波形幅值较高,即背景噪声的去除效果相对较差。包络谱中虽然同样存在明显的110.94 Hz的频率成分,但缺失二阶谐波分量以及其他与故障频率、转频相关的频率成分。

由此可见,该方法对于故障信息的提取能力一般。

为进一步验证基于卡尔曼滤波与子带选取方法的准确性,笔者分别采用该方法与ISVD-RSSD方法对内圈故障信号进行分析,其包络谱对比如图11所示。

图11 内圈故障信号包络谱

图11中,与外圈处理结果类似,相比ISVD-RSSD方法,基于卡尔曼滤波与子带选取的方法能更为有效地提取信号中的故障成分及其谐波分量,可对轴承内圈故障进行准确诊断。

综合上述轴承内外圈故障信号对比结果发现:采用基于卡尔曼滤波与子带选取的方法降噪后的信号时域波形幅值大幅下降,混响噪声被有效消除,且冲击成分增加,包络谱中可读取出明显的故障频率及其相关成分,去噪效果显著;

由于未考虑混响噪声对轴承故障信号的干扰,ISVD-RSSD方法中的RSSD算法的关键参数无法随测量环境变化自适应地得到调整,容易受到混响信号与随机背景噪声的干扰,导致其去噪效果一般。

基于卡尔曼滤波与小波包子带选取的方法采用卡尔曼滤波,有效消除了混响噪声的干扰;同时以不同参数设置下处理所得信号的峭度为指标,达到了关键参数自适应设定的目的,有效提高了直达声信号在分析信号中的占比,减少了因信号不同频段衰减差异及反复叠加引起的信号失真现象,减少了其对诊断结果的影响。

同时,笔者依据待测状态与正常状态信号小波包子带能量值的相对变化,筛选出故障信息最为显著的子带信号,减少了背景噪声(因皮带机其他部件振动产生)对轴承故障信号的干扰。

以上诊断实例及分析结果表明:基于卡尔曼滤波与子带选取的方法可以有效地提取轴承故障成分,实现基于声信号的皮带机齿轮箱轴承故障诊断。

4 结束语

笔者深入分析了皮带输送机齿轮箱轴承运行过程中,声音传感器采集所得信号的组成、声信号产生机理及信号传递路径,提出了一种基于卡尔曼滤波与最优子带选取的声信号增强方法。

轴承故障模拟试验结果表明:

1)声信号增强方法降低了混响信号与背景噪声对轴承信号的干扰,在室内复杂声场环境下,达到了针对皮带机齿轮箱轴承的声信号增强之目的;

2)具有自适应设定参数作用的单通道去混响方法,可以有效地消除狭小空间下的混响信号,可为其他类型机电设备混响噪声的抑制提供一定的借鉴;

3)基于最大能量变化的冲击信号增强方法提高了分析信号中的故障信息占比,对基于振动分析的旋转机械故障诊断研究具有一定的借鉴意义。

在后续的研究中,笔者将进一步分析电机、皮带机托辊等关键部件的声信号特点,以验证基于卡尔曼滤波与子带选取的方法对于其他复杂机电设备的声学特征增强效果。