改进正弦算法引导的蜣螂优化算法
2023-11-27潘劲成李少波杨贵林吕东超
潘劲成,李少波,2,周 鹏,杨贵林,吕东超
1.贵州大学 机械工程学院,贵阳550025
2.贵州大学 省部共建公共大数据国家重点实验室,贵阳550025
长期以来,优化问题一直是研究的重点。所谓优化问题,是指在一定条件下,在多个解或参数值中找到最优解或参数,以优化一个或多个函数[1]。优化问题就是在所有可能的情况中找出最佳的解决方案。优化问题存在于各种现实领域中,包括故障诊断[2]、路径规划[3]、航天[4]以及各种军事工业领域[5-6]等。随着科学技术的不断深入发展,各领域工程优化问题的难度和复杂程度日愈增加,例如在实际工程中,许多设计应用需要在短时间内和高度复杂的约束下获得最优解,这是一项非常具有挑战性的任务[7],因此亟需更加高效的求解算法。学者们通过对自然物理规律和生物习性的观察,已经开发出来各种元启发式算法并用于各种优化问题[8]。元启发式算法可以为各种具有挑战性和复杂的优化问题找到最优解,而且这些元启发式算法具有在较短时间内解决复杂和多维问题的能力[9]。
到目前为止,已经研究了多种元启发式算法来解决现实世界中的优化问题,如遗传算法(genetic algorithm,GA)[10]、粒子群优化(particle swarm optimization,PSO)[11]、差分进化(differential evolution,DE)[12]、灰狼优化算法(grey wolf optimizer,GWO)[13]、鲸鱼优化算法(whale optimization algorithm,WOA)[14]、蝴蝶优化算法(butterfly optimization algorithm,BOA)[15]、麻雀搜索算法(sparrow search algorithm,SSA)[16]、黑猩猩优化算法(chimp optimization algorithm,ChOA)[17]、算数优化算法(arithmetic optimization algorithm,AOA)[18]、人工水母搜索算法(artificial jellyfish search optimizer,JS)[19]。与传统的优化技术相比,这些算法在实际应用方面表现出更好的性能,这些元启发式优化算法具有稳定性强且易于实现等优点,同时在求解复杂优化问题上也具有较好的表现[20]。但是迄今为止,研究人员只使用了非常有限的受自然启发的特征,还有很多算法开发的空间[21]。
蜣螂优化器(dung beetle optimizer,DBO)算法是由Xue 等[22]于2023 年提出的一种新型群体智能优化算法,该算法灵感来源于蜣螂种群的社会行为,即蜣螂的滚球、跳舞、觅食、繁殖和偷窃行为。相较于粒子群优化算法、遗传算法等经典算法,蜣螂优化算法根据蜣螂种群分工划分不同的生存任务,种群中分为滚球蜣螂、繁育蜣螂(繁育球)、小蜣螂、偷窃蜣螂4 种。为了进一步说明DBO 算法的实际应用潜力,Xue 等将DBO 算法成功地应用于多个工程设计问题。实验结果表明,所提出的DBO算法可以有效地处理实际应用问题。总体来说DBO 算法兼顾了全局探索和局部开发,具有收敛速度快、求解精度高的特点。
然而,没有免费的午餐(no free lunch,NFL)定理[23]在逻辑上证明了没有一种元启发式算法适合解决所有的优化问题。这激励人们不断开发新的元启发式算法来解决不同的问题。蜣螂优化算法虽然具有寻优能力强,收敛速度快的特点,但同时也存在全局探索和局部开发能力不平衡,容易产生局部最优,且全局探索能力较弱的缺点。
受改进正弦算法(improved sine algorithm,MSA)[24]的启发,本文把MSA 中的全局探索和局部开发能力赋予蜣螂,同时加入了混沌映射初始化种群和变异算子进行扰动,称这种改进算法为MSADBO。通过比较其他8种元启发式算法在23 个基函数上的应用结果,表明本文提出的算法能加快收敛速度,提高收敛精度,并能找到全局最优而不是局部最优。3个工程问题的应用也证明了本文提出的算法在解决实际问题时具有很大的优势。
本文的主要完成情况总结如下:
(1)在MSA的基础上,对DBO进行了改进,使滚球蜣螂能够自由活动且拥有更强的全局探索能力;
(2)使用混沌映射初始化种群,使用自适应高斯-柯西混合变异算子扰动最优位置;
(3)评估了该算法在23个基准测试函数上的性能,并与其他8种算法进行了比较;
(4)通过3个工程应用设计问题来评估本文提出的算法解决实际问题的有效性。
1 蜣螂优化器
本章简要介绍了DBO 的来源、数学模型和相应的算法。蜣螂优化算法的思想来自于蜣螂的滚球、跳舞、觅食、繁殖和偷窃行为的启发,设计了5 种不同的更新规则,以帮助找到高质量的解决方案。
1.1 滚球蜣螂
蜣螂有一个有趣的习惯,把粪便做成球,然后把它滚到理想位置,在滚动过程中,蜣螂需要通过天体线索(太阳位置或风向等)来保持粪球在直线上滚动。为了模拟滚球行为,蜣螂需要在整个搜索空间中沿给定方向移动。在滚动过程中,滚动球的蜣螂的位置会更新,滚动数学模型可以表示为:
其中,t表示当前迭代次数,xi(t)表示第i只蜣螂在第t次迭代时的位置信息,k∈(0,0.2]表示偏转系数的常量,b表示属于(0,1) 的常量,α是一个自然系数,赋值为-1或1(参见算法1),Xw表示全局最差位置,Δx用于模拟光强的变化。
算法1α的选择策略
当蜣螂遇到障碍物而无法前进时,它需要通过跳舞来调整自己的方向,以获得新的路线。使用切线函数来模拟蜣螂的舞蹈行为,获得新的滚动方向。一旦蜣螂成功地确定了一个新的方向,它就会继续向前滚动球。因此,蜣螂跳舞行为的位置被定义如下:
其中,θ∈[0,π],如果θ等于0、π/2 或π 时,将不会更新蜣螂的位置。
1.2 繁育蜣螂(繁育球)
在自然界中,粪球被滚到安全的地方,并被蜣螂藏起来。为了给它们的后代提供一个安全的环境,选择合适的产卵地点对蜣螂来说至关重要。受上述讨论的启发,提出了一种边界选择策略来模拟雌性蜣螂产卵的区域,该策略为:
其中,X*表示当前局部最佳位置,Lb*和Ub*分别表示产卵区的下界和上界,R=1-t/Tmax,Tmax表示最大迭代次数,Lb和Ub分别表示优化问题的下界和上限。
一旦确定了产卵区,雌性蜣螂就会选择这个区域的繁育球产卵。应该提到的是,对于DBO算法,每只雌性蜣螂在每次迭代中只产一个卵。此外,从式中可以清楚地看出,产卵区的边界范围是动态变化的,这主要由R值决定。因此,繁育球的位置在迭代过程中也是动态的,迭代过程表示为:
其中,Bi(t)是第t次迭代时第i个繁育球的位置信息,b1和b2表示两个大小为1×D的独立随机向量,D表示优化问题的维数。繁育球的位置被严格限制在一定范围内,即产卵区(参见算法2)。
算法2繁育球位置更新策略
如图1 所示,蓝色的点代表滚球蜣螂的位置,当前局部最佳位置X*使用一个棕色的大圆圈来表示,而X*周围的黑色小圆圈表示繁育球。每个繁育球中都有一个蜣螂的卵。此外,红色的小圆圈表示边界的上限和下限。
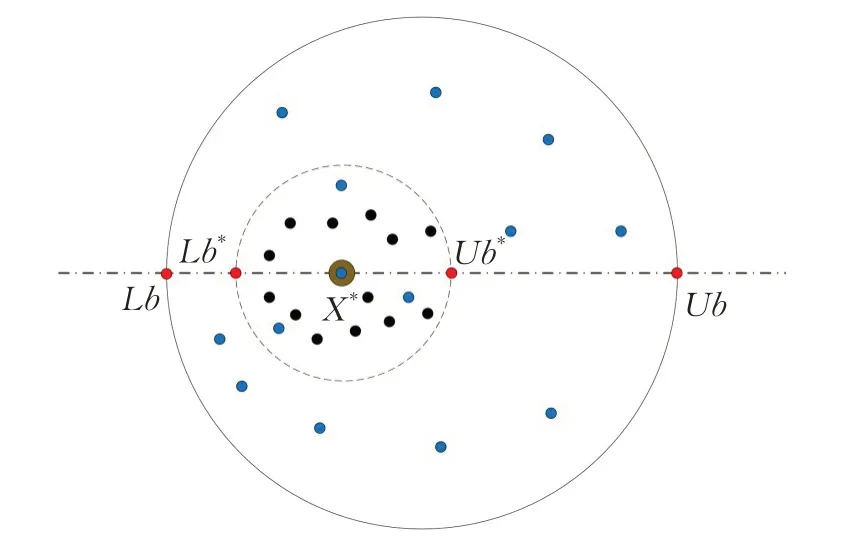
图1 边界选择策略的概念模型Fig.1 Conceptual model of boundary selection strategy
1.3 小蜣螂
一些已经长成成虫的蜣螂从地里爬出来寻找食物,称它们为小蜣螂。此外,还需要建立最佳觅食区来引导蜣螂觅食,这模拟了这些蜣螂在自然界中的觅食过程。具体而言,最佳觅食区域的边界定义如下:
其中,Xb表示全局最佳位置,Lbb和Ubb分别表示最佳觅食区域的下限和上限,其他参数在公式中定义。因此,小蜣螂的位置更新如下:
其中,xi(t)表示第i只小蜣螂在第t次迭代的位置信息,C1表示服从正态分布的随机数,C2表示属于(0,1)的随机向量。
1.4 偷窃蜣螂
一些被称为小偷的蜣螂从其他蜣螂那里偷粪球。从式中可以看出,Xb是最佳的食物来源。因此,可以假设Xb附近是争夺食物的最佳地点。在迭代过程中,偷窃蜣螂的位置信息被更新,可以描述如下:
其中,xi(t)表示第i只偷窃蜣螂在第t次迭代时的位置信息,g是服从正态分布的大小为1×D的随机向量,S表示一个常量。
在前面讨论的基础上,所提出的DBO 算法的伪码如算法3所示。首先,设Tmax为最大迭代次数,N为粒子总体的大小。然后,随机初始化DBO 算法的所有代理,其分配设置如图2所示。图中扇形比例图代表蜣螂中每个代理部分的占比(各个代理比例可以根据具体情况进行调节),滚球蜣螂占比为20%,繁育球占比为20%,小蜣螂占比为25%,偷窃蜣螂占比为35%。在实验中假设物种规模为30。具体而言,蓝色、黄色、绿色和红色的矩形分别代表滚球蜣螂、繁育球、小蜣螂和偷窃蜣螂。

图2 DBO算法中各个搜索代理的比例分布Fig.2 Proportional distribution of search agents in DBO algorithm
算法3DBO算法
之后,根据算法3的第2~27步,在优化过程中,滚球蜣螂、繁育球、小蜣螂和偷窃蜣螂的位置会不断更新。最后,输出最佳位置Xb及其适应度值。总之,对于任何优化问题,DBO算法作为一种新的元启发式优化算法,主要有6个步骤,大致可以概括如下:
(1)初始化蜣螂群和DBO算法参数;
(2)根据目标函数计算所有蜣螂的适应度值;
(3)更新所有蜣螂的位置;
(4)判断各个蜣螂是否在边界外;
(5)更新当前最优解及其适应度值;
(6)重复上述步骤,直到t满足终止准则,输出全局最优解及其适应度值。
2 蜣螂优化器算法改进
2.1 改进动机
在优化问题上,DBO算法优于其他算法。然而,对于DBO 来说,获得理想的最优解仍然极具挑战性。此外,它解决复杂问题的能力也不尽如人意。蜣螂优化算法虽然具有寻优能力强、收敛速度快的特点,但同时也存在全局探索和局部开发能力不平衡,容易陷入局部最优,且全局探索能力较弱的缺点。因此,为了提高DBO的搜索性能,本章提出了3 种加强DBO 的策略。原有的DBO 算法无法很好地平衡探索和开发两个阶段。MSADBO 算法通过Bernoulli 映射策略、嵌入改进正弦算法策略和自适应的高斯-柯西变异扰动来改善这种不平衡。本章将具体介绍这些策略。
2.2 混沌映射初始化种群
混沌映射是一种确定性和随机性相结合的方法,混沌具有随机性、非周期性等特点[25]。由于混沌变量在初始化位置更新过程中取代了智能算法运行过程中的随机变量,混沌映射策略对解空间的搜索范围比随机搜索策略更广。因此,对于随机初始化过程,混沌初始化可以提高优化算法的搜索广度。
蜣螂优化算法是在搜索空间中随机初始化种群的位置,但是该方法有3个主要缺点:
(1)蜣螂个体的位置分布不均匀;
(2)全局探索能力较弱;
(3)种群多样性低而容易陷入局部最优。
为了提高种群初始解的多样性,在DBO 的种群初始化阶段使用混沌映射来生成高度多样化的初始种群。目前存在多种不同的混沌映射[26],主要有Singer映射、Chebyshev映射、Bernoulli映射、Gaussian映射、PWLCM映射等。其中Bernoulli映射属于混沌映射的一种,常被用来产生混沌序列,其具有非线性、遍历性、随机性等特征,在优化领域替代随机数初始化种群,会影响算法的整个过程,同时能获得比随机数更好的寻优效果[27]。此外Saito等[28]研究表明,Bernoulli映射的遍历均匀性和收敛速度适合作为混沌种群初始化,并通过合理的实验设置,证明了Bernoulli映射可以用于产生优化算法的初始种群,Bernoulli 映射混沌序列分布如图3 所示。因此本文采用Bernoulli 映射初始化蜣螂个体位置,先利用Bernoulli映射关系将所得的值投影到混沌变量空间内,然后将产生的混沌值通过线性变换映射到算法初始空间中。Bernoulli映射具体表达式为:

图3 Bernoulli映射混沌序列分布Fig.3 Distribution of chaos values for Bernoulli map
其中,β是映射参数,β∈(0,1) 。文中设置β=0.518,z0=0.326,以达到最好的取值效果。
2.3 利用改进正弦算法
改进正弦算法(MSA)[24]策略是受到正余弦算法(sine cosine algorithm,SCA)[29]、正弦算法(sine algorithm,SA)[30]和指数正余弦算法(exponential sine cosine algorithm,ESCA)函数[31]以及改进的正弦余弦算法(improved sine cosine algorithm,ISCA)[32]等各类与SCA相关算法的启发,利用数学中的正弦函数进行迭代寻优,具有较强的全局探索能力。同时在位置更新过程中引入自适应的可变惯性权重系数ωt,使算法能够对局部区域进行充分搜索,使全局探索和局部开发能力达到良好的平衡。改进正弦算法位置更新公式如下所示:
其中,t为当前迭代次数,ωt是惯性权重,xi(t)为个体X在第t次迭代中的第i个位置分量,pi(t)为第t次迭代中最佳个体位置变量的第i个分量,r1为非线性递减函数,r2是区间[0,2π]上的随机数,r3是区间[-2,2]上的随机数。
使用非线性递减模式来设置r1的值,并使用0到π之间的余弦函数来确定r1值的变化:
其中,ωmax和ωmin表示ωt的最大值和最小值,t表示当前迭代次数,Tmax表示最大迭代次数。
采用了自适应的可变惯性权重策略,其中惯性权重随着迭代次数的增加线性减小:
为进一步改进DBO算法协调全局探索与局部开发的能力,本文引入了正弦引导机制,MSA作为替代蜣螂正切跳舞的策略嵌入DBO 算法,即在滚球阶段对整个蜣螂个体进行正弦的操作引导蜣螂位置更新。改进后的公式如下:
其中,δ=rand(1),ST∈(0.5,1]。改进后的位置更新公式中,当δ <ST时,表明蜣螂有目标地进行滚动,处于正常全局探索阶段,而当δ≥ST时,代表蜣螂没有明确的滚动目标,但是会通过一种正弦函数的方式进行搜索移动。
这种改进正弦指引机制的引入,一方面可以极大地改善DBO算法位置更新策略过于随机的缺陷。这是由于加入MSA 策略后,蜣螂个体会与当前最优个体pi(t)进行信息交流,促进信息在种群中快速传播,改善了原算法中缺乏个体间信息交流的缺陷。
另一方面,针对原算法容易陷入局部最优的问题,MSA的指引机制使得蜣螂个体可以自由在算法给定的区域范围内进行全局探索和局部寻优,在一定程度上扩大了搜索空间,并逐渐收敛于同一个最优解即目标函数值,从而提升算法的全局寻优能力。同时由公式可以看出,r1控制蜣螂的搜索距离和方向,优化了DBO算法的寻优方式,并且自适应系数ωt逐步缩小了搜索空间,随着迭代次数的增加,惯性权值减小。在算法迭代前期相对较大的惯性权值能使算法拥有较强的全局探索能力,而迭代后期相对较小的惯性权值则有助于提高其局部开发能力。
2.4 自适应高斯-柯西混合变异扰动
在基本蜣螂算法迭代的后期,蜣螂个体快速同化,蜣螂群体迅速聚集到当前的最优位置附近,其值近似于最优解。因此,如果当前最优位置不是全局最优的点,那么蜣螂种群会集中在当前最优位置附近搜索,导致无法发现真正的最优位置,出现搜索停滞的情况。为解决这一问题,一般采用变异扰动操作对个体进行干扰以增加种群多样性,跳出局部最优[33]。执行变异扰动操作能够提高蜣螂种群多样性,使算法能够跳出局部最优解,进入解空间的其他区域继续进行勘探,直至最终找到全局最优解。
在智能优化算法中引入变异算子,既可以增强种群的多样性,又可以使算法避免陷入局部极小[34]。柯西变异和高斯变异是智能优化算法中两种较常用的变异算子,这两种变异算子都有各自的优缺点。柯西变异的搜索范围要比高斯变异的搜索范围大,但其过大的步长容易跳离最优值而产生较差的后代[35];而高斯变异在小范围内具有良好的搜索能力[36],这是因为其能以较大的概率产生较小的变异值。所以提出了一种融合柯西变异和高斯变异各自优点的自适应高斯-柯西混合扰动变异扰动策略。
由于变异扰动操作的结果具有随机性,若对所有蜣螂均进行变异扰动操作必然会增加算法的复杂度,因此本文仅对最优个体进行变异扰动,然后比较其变异前后的位置,选择较好的位置进入下一次迭代,充分增加蜣螂的多样性,扩大种群搜索范围。具体公式如下:
其中,Xb(t)为个体X在第t次迭代中的最优位置,Hb(t)为第t次迭代中的最优位置Xb(t)在高斯-柯西混合扰动后的位置,Gauss(σ)为高斯变异算子,Cauchy(σ)为柯西变异算子,μ1=t/Tmax,μ2=1-t/Tmax,变异算子的权重系数μ1、μ2以一种一维线性的方式逐步变动,目的是保证每一次的迭代扰动均衡平滑。
在算法迭代过程中对蜣螂个体进行变异扰动,算法迭代初期,由于种群分布比较分散,算法主要通过柯西分布函数对个体进行较大幅度变异扰动,从而产生多样性个体,既充分利用了当前位置信息,又增加了随机干扰信息,使算法能够进行全局探索,快速收敛;随着算法迭代的不断进行,蜣螂大多数个体位置不会发生太大变化,此时算法主要通过高斯分布函数系数对种群进行扰动,从而帮助算法能够跳出局部自由度,同时克服了高维问题下的维间干扰问题。总而言之,自适应高斯-柯西混合变异扰动策略,使用了柯西和高斯分布函数的特性来产生新的个体,增强了蜣螂的多样性,增强了算法协调其局部开发和全局探索的能力。
自适应高斯-柯西混合扰动变异扰动策略虽然能增强算法全局搜索和跳出局部最优的能力,但是没法确定变异扰动之后得到的新位置一定比原位置的适应度值要好,因此在进行变异扰动更新后,加入贪婪规则[34],通过比较新旧两个位置的适应度值,确定是否要更新位置。贪婪规则如下所示,f(x)表示x位置的适应度值。
2.5 MSADBO流程图
MSADBO流程如图4所示。
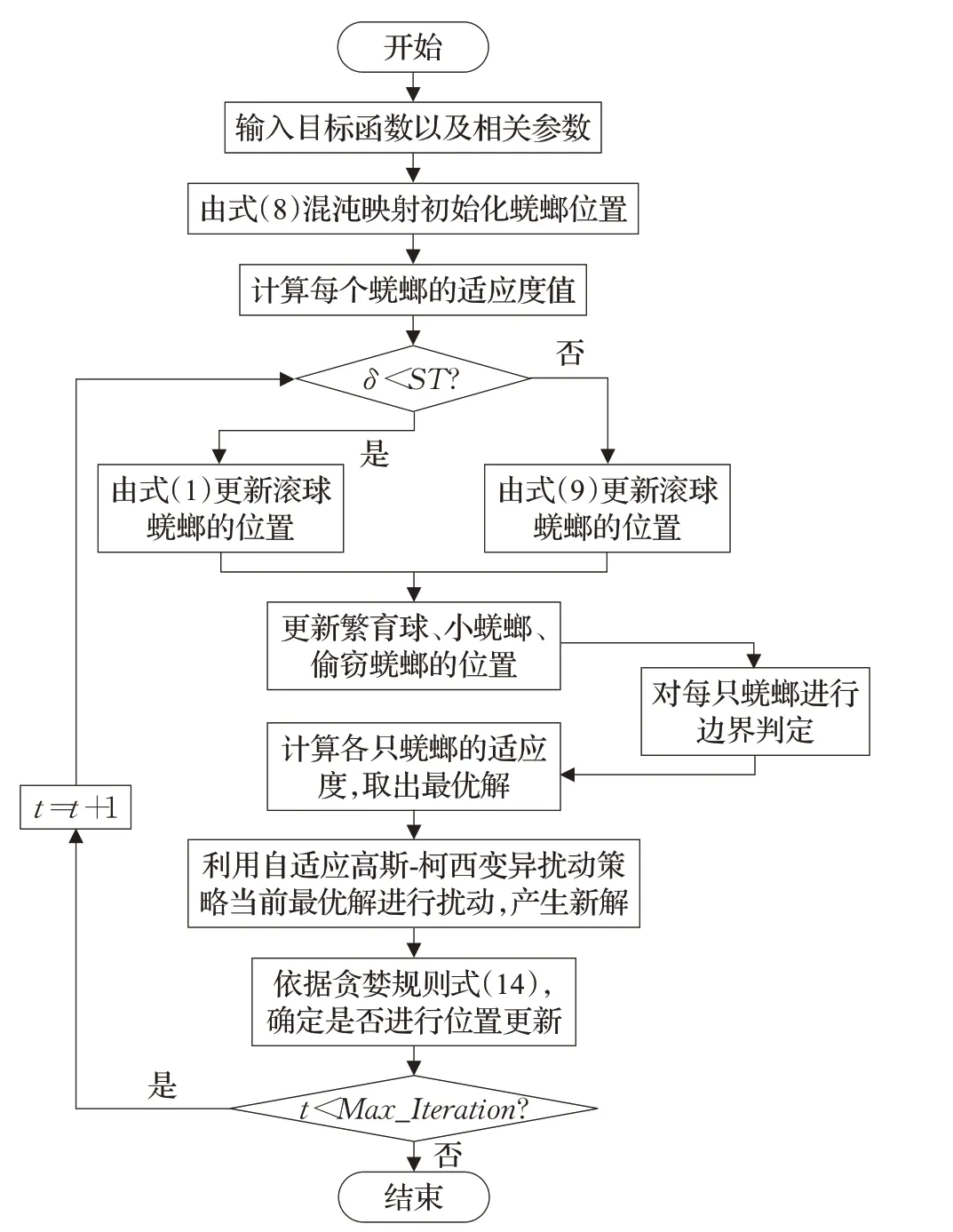
图4 MSADBO流程图Fig.4 Flowchart of MSADBO
2.6 MSADBO复杂度分析
算法分析的目的是选择合适的算法和改进算法,时间复杂度是算法收敛速度的重要指标之一[37]。本文选择大O表示法计算时间复杂度[38]。
大O表示法的推导方法如下:
(1)将运行时的所有附加常数替换为常数1;
(2)在修改后的运行时间函数中,只保留最高阶的项目;
(3)如果最高阶项存在且不为1,则去掉乘以该项的常数。结果是一个大O顺序。
根据上述计算方法,本节选取蜣螂优化(DBO)和改进正弦算法引导的蜣螂优化算法(MSADBO)为对比算法。DBO的计算结果为O(N×D×T)。同样,MSADBO在计算过程中没有引入新的循环,也没有改变其顺序。因此,结果仍然是O(N×D×T)。
通过10 次时间对比实验,每次算法迭代1 000 次,得到算法运行时间,实验结果如表1所示。DBO算法每迭代1 000 次CPU 平均运行时间为0.138 7,MSADBO算法每迭代1 000次CPU平均运行时间为0.146 2,两个算法CPU运行时间基本相同。
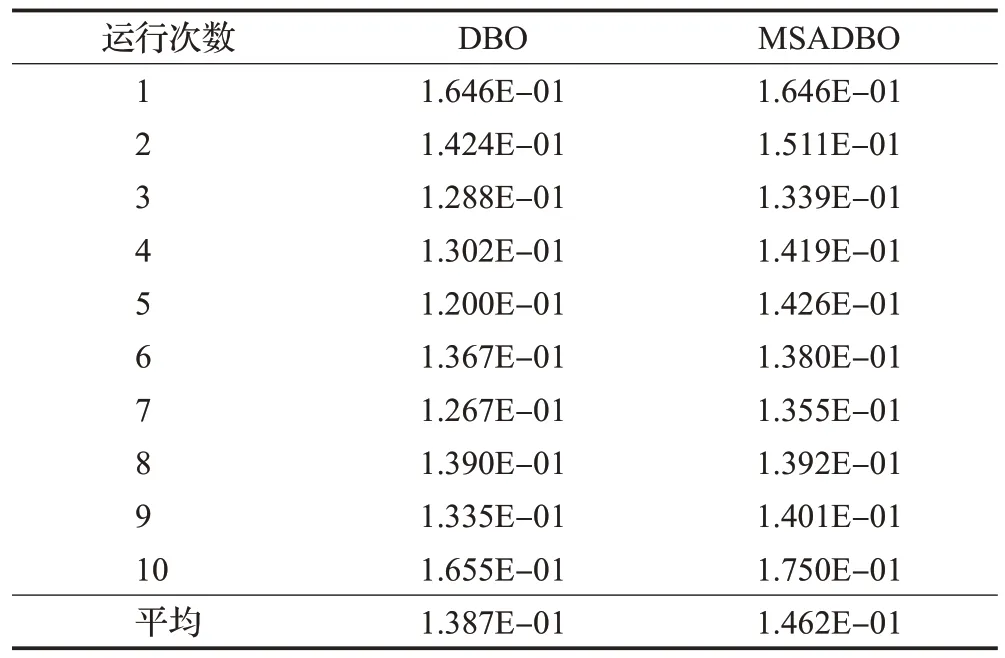
表1 DBO和MSADBO算法CPU运行时间对比Table 1 Comparison of CPU running time between DBO and MSADBO algorithms
3 实验结果和讨论
3.1 实验准备
本节中MSADBO基于23个基准函数,并与其他10个基准函数进行比较。这些函数已经在许多文献中得到了验证[39]。本文仿真实验的操作系统均为Windows11操作系统,CPU 为12th Gen Intel®CoreTMi7-12700H,主频为2.30 GHz,内存为16 GB(4 800 MHz),显卡为NVIDIA GeForce RTX 3060 Laptop GPU,编程软件为MATLAB R2020b。本文中搜索代理的数量统一设置为30个,最大迭代次数为500,每个算法独立运行30次。
寻找这些函数的最小值类似于搜索代理寻找猎物最小值的位置。本文的目标是找到可能的最小值的适应度函数。首先,算法在搜索空间中生成初始种群,以设定的方式进行搜索。本节除了选取MSADBO算法进行实验外,还选取了许多完善的优化算法,包括SSA[16]、DBO[22]、GWO[13]、PSO[11]、SCA[26]、ChOA[17]、MSA[24]、BOA[15]作为对比算法。通过在23 个基准函数中比较最佳值(Best)、平均值(Average)和标准差(STD)来验证本文提出的MSADBO 算法的优越性。之所以选择这些方法,是因为它们在探索和开发方面具有广泛的性能特点。
其中MSADBO 算法包含三方面的改进:Bernoulli映射策略、嵌入改进正弦算法策略和自适应的高斯-柯西变异扰动。为了验证本文提出的不同改进策略的独立有效性,将DBO与这3个策略分别结合得到3种不同算法:
(1)DBO 中加入Bernoulli 映射策略初始化种群后得到MDBO1;
(2)DBO嵌入改进正弦算法策略后得到MDBO2;
(3)DBO 最后加入自适应的高斯-柯西变异扰动后得到MDBO3。
将DBO 与MDBO1、MDBO2、MDBO3、MSADBO四种改进算法进行实验对比,通过在单峰基准函数中比较最佳值(Best)、平均值(Average)和标准差(STD)来验证每个改进策略的有效性。其中基准函数维度统一设置为30。
表2总结了对应算法的参数设置。需要注意的是,这些参数的值是根据参考论文的建议设置的。本文提出的MSADBO算法的参数中ωmax和ωmin表示ωt的最大值、最小值,k∈(0,0.2]表示偏转系数的常量,b表示属于(0,1) 的常量。这些算法参数可以根据不同的应用环境在合理的区间内进行调整。本文经过大量的实验对比,选取ωmax=0.9,ωmin=0.782,k=0.1,b=0.3 可以达到最均衡的效果。

表2 参数变量设置Table 2 Parameter values setting
3.2 单峰函数分析
3.2.1 MSADBO与其他各类算法对比
表3 给出了7 个单峰基准测试函数(F1~F7)。表中fmin为函数最佳适应度值。由于单峰函数有且只有一个最小值,可以用来检验算法的开发性能。表4~表6中的F1~F7给出了各个算法在不同维度下的性能。对于函数F1~F4和F7,MSADBO 算法都寻找到了最优解。在整体优化结果的均值上以及最优值中排在第一位,体现了MSADBO 算法优秀的局部开发性能。对于函数F5、F6,MSADBO 算法的适应度值虽然不是最好的,但也是排在几种算法前列。结果表明,在局部开发能力中,提出的算法在大多数函数上比一些知名算法执行得更好(最好的结果用粗体显示)。

表3 单峰基准函数Table 3 Unimodal benchmark functions

表4 F1~F13 的实验结果(维度=30)Table 4 Experimental results of F1~F13(dim=30)
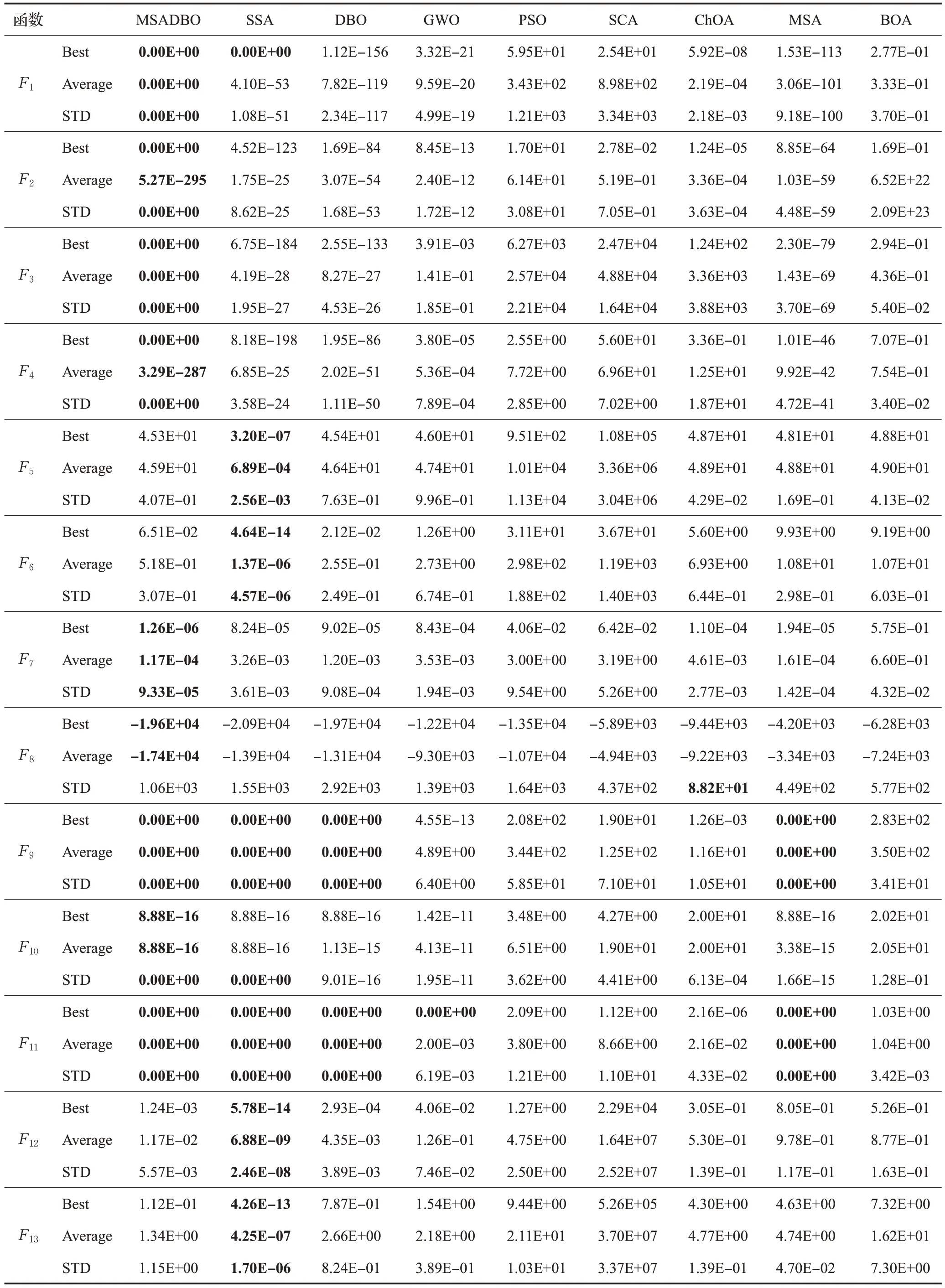
表5 F1~F13 的实验结果(维度=50)Table 5 Experimental results of F1~F13(dim=50)
3.2.2 MSADBO中各种策略有效性验证
表7给出了DBO与4种改进算法MDBO1、MDBO2、MDBO3、MSADBO 的实验结果对比。图5 给出了各个算法策略对比的收敛过程图像。结合表7中数据和图5可以看出:
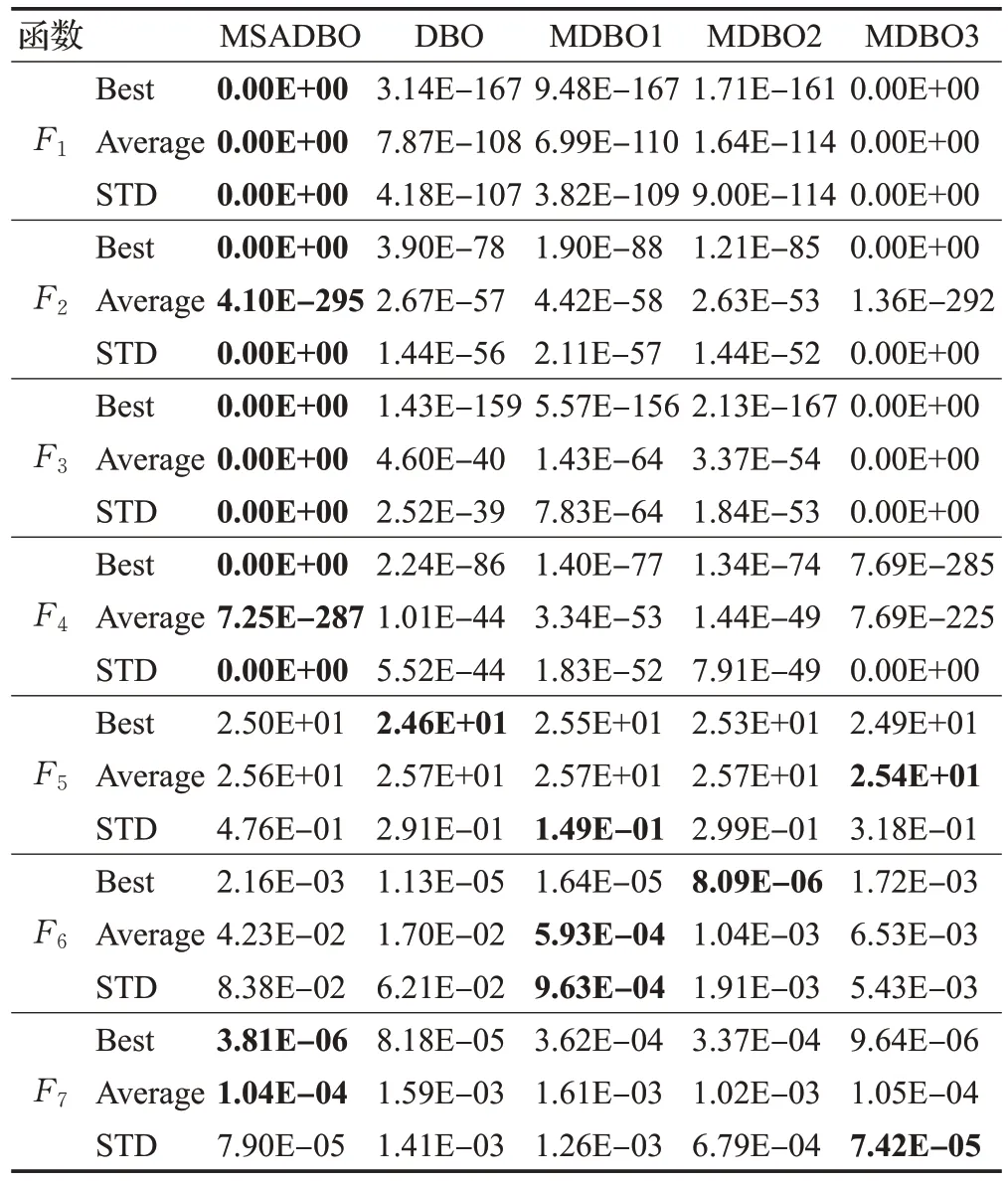
表7 单峰基准函数的实验结果(各个策略对比)Table 7 Experimental results of unimodal benchmark function(Comparison of various strategies)

图5 不同算法的收敛过程(各个策略对比)Fig.5 Convergence process of different algorithms(Comparison of various strategies)
(1)MDBO1 算法相比较原始DBO,虽然收敛曲线相似,那是由于它们除了种群初始化策略不同外,其他近乎相同,但是MDBO1在求解精度上有了一定程度的提升,平均寻优性能更加稳定。说明引入Bernoulli映射策略提升了算法全局探索能力,能生成高度多样化的蜣螂初始种群。
(2)MDBO2 算法相比较DBO,平均寻优精度和标准差有了更进一步的提升,同时收敛曲线在收敛速度变慢时逐渐深入开发。说明DBO嵌入改进正弦算法策略后,能够很好地平衡全局探索和局部开发能力。
(3)MDBO3 算法相比较DBO,使得算法的收敛速度和收敛深度有了很大幅度的提高。说明加入自适应的高斯-柯西变异算子能够大幅提高算法的开发能力。同时其收敛曲线快速收敛,表明自适应高斯-柯西变异策略能够有效避免算法陷入局部最优解,提高算法的寻优能力。
(4)MSADBO算法相比其余策略算法,融合了MDBO1的寻优稳定性,增添初始种群多样性;融合了MDBO2的平衡全局探索和局部开发能力;融合了MDBO3的快速迭代寻优能力,同时避免了局部最优解。总体来说MSADBO 算法不仅能够快速收敛,而且拥有平衡探索与开发的能力,拥有跳出局部最优解的能力。
3.3 多峰函数分析
表8给出了6个多峰函数(F8~F13)。与单峰函数不同,多峰函数具有多个极值,且随维数的增加而增加。因此,多峰函数可以用来评估算法的探索能力。表4~表6 中的F8~F13给出了各个算法在不同维度下的性能。对于函数F8~F11,MSADBO算法都快速地找到了最优值并且进行了深入开发,所提出的NIPSO在上述多模态高维函数上可以实现更高的寻优精度。可以看出,MSADBO算法在寻找多峰函数最优解的过程中具有更好的探索能力。结果表明,在探索能力方面,提出的算法在大多数函数上比一些知名算法执行得更好(最好的结果用粗体显示)。

表8 多峰基准函数Table 8 Multimodal benchmark functions
F14~F23也是多峰函数,它们的函数表达式如表9所示。但因为它们的维数是固定的,所以它们的结果分别如表10 所示。在各种维度的多峰函数中,MSADBO算法都能够精确地寻找到最优值,能在全局探索和局部开发中自适应转换。通过对比发现,本文提出的算法在开发能力和探索能力方面取得了很好的平衡(最好的结果用粗体显示)。
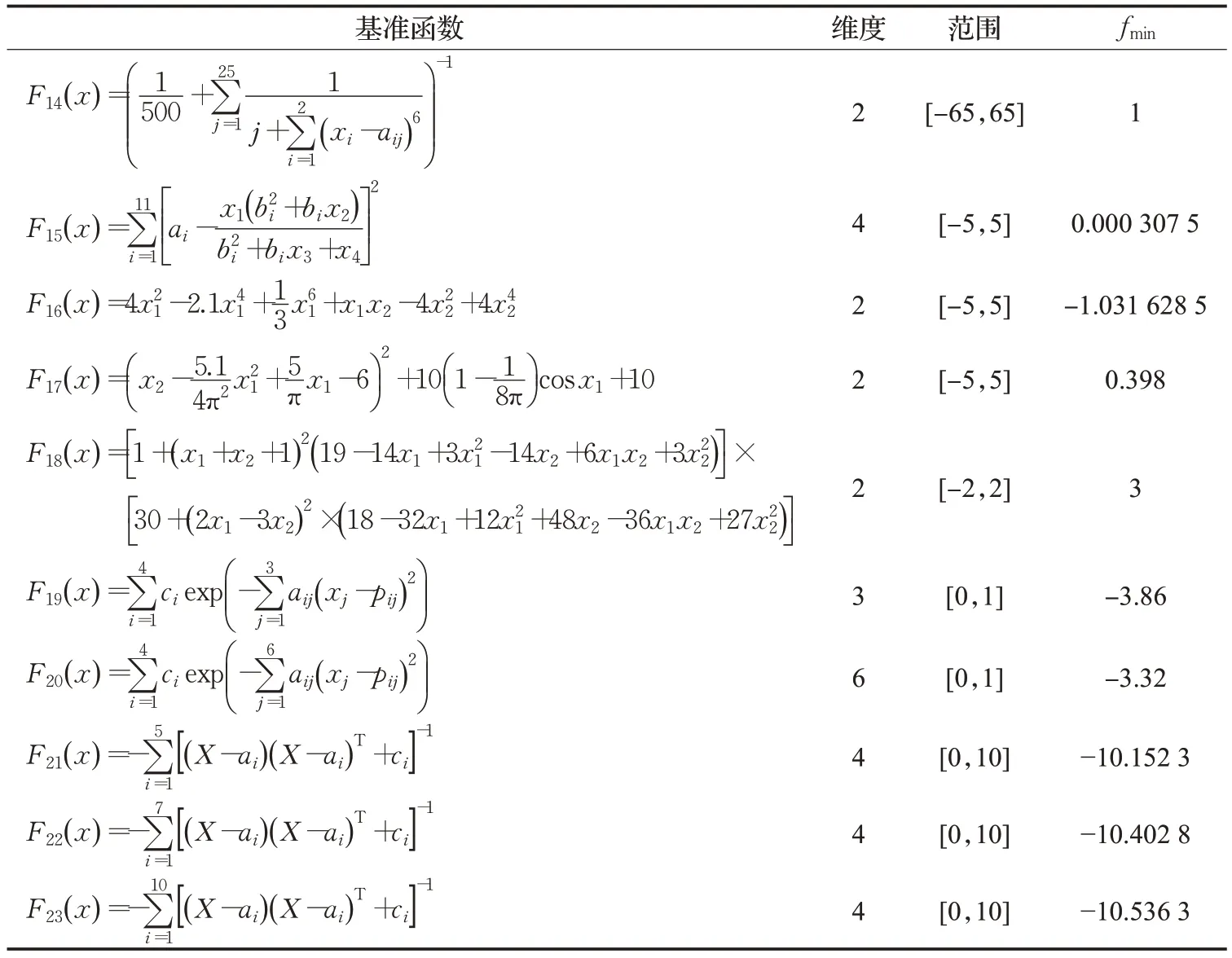
表9 固定维多峰基准函数Table 9 Fixed-dimension multimodal benchmark functions
同时,图6显示了不同算法在迭代过程中的收敛过程。在大多数测试函数图中,可以看到MSADBO 算法的收敛速度是拥有绝对优势的,并且拥有很高的收敛精度。无论是在单峰函数还是多峰函数中,MSADBO 算法都拥有非常优秀的表现,能够快速搜索收敛,并且能够进一步深入开发,表现了MSADBO算法全局探索能力和局部开发能力的合理平衡。通过对比发现,MSADBO算法不仅最终收敛精度优于其他算法,而且收敛速度也快于其他算法。
3.4 统计分析秩和检验
在上述统计过程中,计算了每种算法的30 个实验结果的平均值和标准差,以比较算法的优越性。为了进一步比较所提算法与其他算法的差异,进行了统计检验,所采用的方法称为Wilcoxon秩和非参数统计检验[40]。通过计算p值来确定统计结果的显著性。如果p值小于0.05,就能确定两种算法之间存在显著差异。计算结果见表11。其中大于0.05 的值用下划线表示。NaN 表明这两种算法的结果太相似而不显著。差异显著的数据总数在最后一列统计。
表11 中只列出了几个NaN 标记和下划线值,表明基于基准函数的MSADBO算法与竞争对手的搜索结果相似度较低。因此,MSADBO 算法在23 个基准函数上的优化性能与其他元启发式算法、基本DBO 的优化性能有显著差异。结合本章的分析可以看到,在众多元启发式算法中,MSADBO算法的综合性能是最突出的。
4 工程应用设计问题
本文使用了3个工程设计问题来测试MSADBO算法,包括压力容器设计问题(pressure vessel design problem,PVD)[41]、焊接梁设计问题(welded beam design problem,WBD)[42]、拉伸/压缩弹簧设计问题(tension/compression spring design problem,TCSD)[43]。
这3 个问题都是典型的工程优化问题。主要思想是将实际的优化问题转化为数学模型,然后利用各个算法找到最优解。f(x)是原始算法中的适应度函数,x表示搜索空间,x1,x2,…,xn表示不同维度。最终目标是在满足各种机械性能的基础上,尽量减少材料的使用。它们有一些相同或不相同的约束,应该有一个处理约束的方法,以便适用于这些工程问题。因此,最简单的约束处理方法(惩罚函数)可以有效地用于处理算法中的约束。也就是说,如果搜索代理违反了任何约束,它将被分配一个大的目标函数值。这样,在下一个迭代之后,它将自动被一个新的搜索代理替换。接下来是详细的问题描述和实验结果。
4.1 压力容器设计问题
如图7 所示,本设计在满足使用要求的同时,最大限度地降低容器的制造成本。需要优化的变量有4个,分别是壳体厚度Ts、封头厚度Th、内半径R、不考虑封头的圆柱截面长度L。

图7 压力容器设计问题Fig.7 Pressure vessel design problem
数学模型如下所示:
目标函数:
约束条件:
取值范围:
x1和x2是0.062 5的整数倍,10 ≤x3,x4≤200
MSADBO与SSA[16]、DBO[22]、GWO[13]、PSO[11]、SCA[26]、ChOA[17]、MSA[24]、BOA[15]进行了比较。从表12的结果可以看出,MSADBO 算法在解决压力容器设计问题方面排名第一,总成本最小。
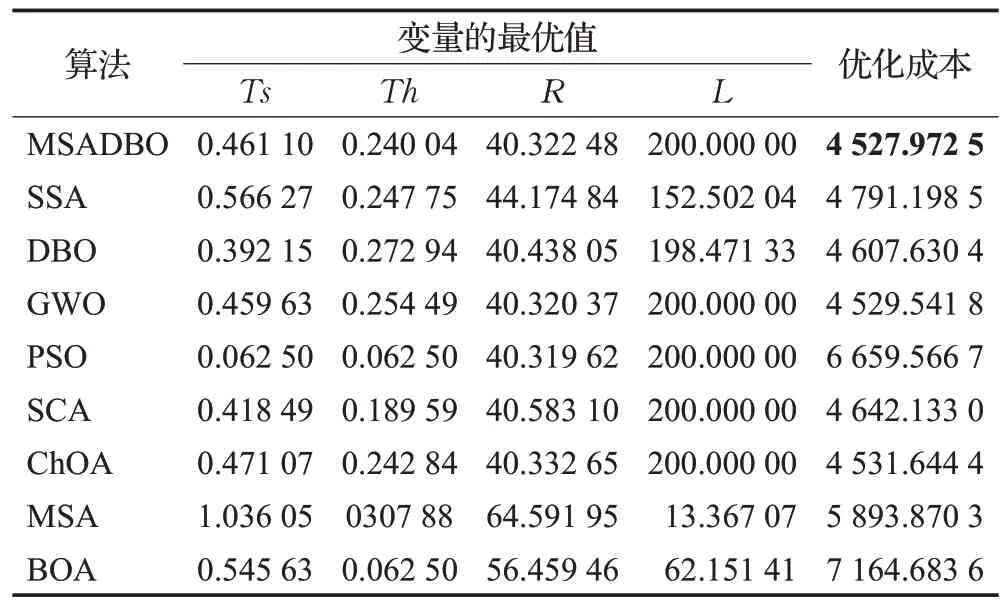
表12 PVD问题MSADBO的比较结果Table 12 Comparison results of MSADBO for PVD problem
4.2 焊接梁设计问题
焊接梁设计的目标是最大限度地降低焊接梁的成本。如图8所示,主要优化变量为焊缝厚度h、钢筋厚度b、钢筋连接部分长度l和钢筋高度t。

图8 焊接梁设计问题Fig.8 Welded beam design problem
最小化过程受到剪切应力τ、梁内弯曲应力θ、杆上屈曲荷载Pc、梁端挠度δ和侧方约束等条件的约束。
数学模型如下所示:
目标函数:
约束条件:
取值范围:
MSADBO与SSA[16]、DBO[22]、GWO[13]、PSO[11]、SCA[26]、ChOA[17]、MSA[24]、BOA[15]进行了比较。从表13的结果中可以看出,MSADBO 在解决焊接梁设计问题中排名第一,总成本最小。
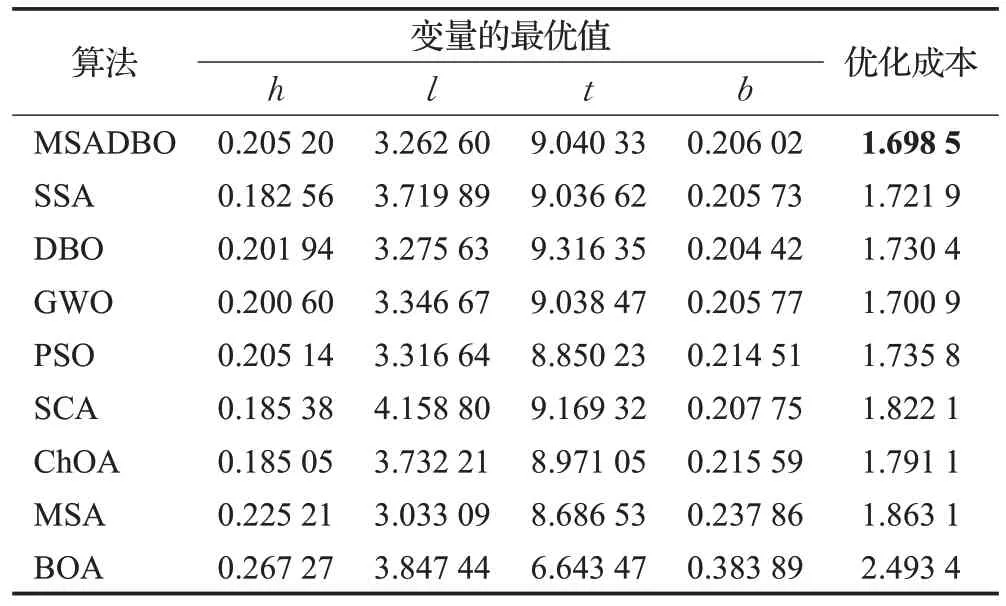
表13 MSADBO对WBD问题的比较结果Table 13 Comparison results of MSADBO for WBD problem
4.3 张力/压缩弹簧的设计问题
张力/压缩弹簧的设计问题是通过选择导线直径d、平均线圈直径D和活动线圈数N,使张力/压缩弹簧的重量最小,如图9所示。

图9 张力/压缩弹簧设计问题Fig.9 Tension/compression spring design problem
最小化过程问题受到最小挠度、剪切应力、浪涌频率、外径和设计变量的限制。设计变量为导线直径d、平均线圈直径D和活动线圈数N。
数学模型如下所示:
目标函数:
约束条件:
取值范围:
MSADBO与SSA[16]、DBO[22]、GWO[13]、PSO[11]、SCA[26]、ChOA[17]、MSA[24]、BOA[15]进行了比较。从表14的结果中可以看出,MSADBO 在解决张力/压缩弹簧的设计问题方面排名第一,总成本最小。

表14 MSADBO对TCSD问题的比较结果Table 14 Comparison results of MSADBO for TCSD problem
5 结论和未来工作
本文提出了一种改进的蜣螂优化器MSADBO。主要目的是让滚球蜣螂嵌入改进正弦算法,从而扩大搜索范围。同时加入了混沌映射初始化种群和变异算子进行扰动,发扬了蜣螂的局部开发能力和改进正弦算法的全局探索能力,平衡了探索与开发能力,使得MSADBO算法能够跳出局部最优解。
采用23 个标准基函数对MSADBO 性能进行了测试。实验结果表明,MSADBO 算法比多种元启发式优化算法具有更快的收敛速度和更高的收敛精度,以及更强的鲁棒性。此外,该算法还应用于压力容器设计、悬臂梁设计和拉/压弹簧设计等实际工程问题。各种实验结果表明,本文提出的MSADBO算法拥有显著的效果。
基于MSADBO 算法的良好性能,计划将其应用于未来的工作中,以解决其他实际和工程问题,例如:
(1)文本和数据挖掘应用;
(2)神经网络的特征选择;
(3)图像处理应用;
(4)云服务组合的协调设计;
(5)灵活车间的多智能体任务分配。
此外,该算法具有收敛速度快、搜索精准、鲁棒性强等特点,适用于未知空间搜索的挑战性问题,因此被认为未来可以应用于移动设备,例如无人机的路径规划。
