行人GNSS/PDR组合导航优化估计方法
2023-11-27朱建良王立雅薄煜明
朱建良, 王立雅, 薄煜明
(南京理工大学 自动化学院, 江苏 南京 210094)
0 引言
随着半导体设计和制造技术的飞速发展,采用微机电系统技术的传感器的体积和功耗获得了显著下降。目前,智能手机嵌入了各种传感器,如加速度计、陀螺仪、视觉摄像头、磁传感器、Wi-Fi、蓝牙、全球卫星导航系统(GNSS)接收机等[1-2]。为了满足行人和单兵等室内外定位、导航需求,基于智能手机的多传感器信息构建无缝导航和定位系统已经成为研究热点[3-4]。在这些传感器中,GNSS接收机能够在户外信号良好的场景下为用户提供精确的定位和导航信息[5-6]。在开阔的天空环境下,视野内拥有足够多的GNSS卫星可以计算出高精度位置信息。然而,在信号具有挑战性的环境中,GNSS信号可能会因环境而恶化,例如隧道中的GNSS信号阻塞、城市地区的多路径信号和非视距(NLOS)信号等[7-8]。信号阻塞导致GNSS接收机无法定位,多路径信号和NLOS信号会导致GNSS定位精度下降。因此,在构建基于智能手机的行人/单兵无缝定位系统时,基于GNSS/惯性导航系统(INS)的组合导航系统是提供更可靠导航解决方案的基石[9-10]。
智能手机中嵌入了带有三轴加速度计和陀螺仪的惯性测量单元(IMU)来测量智能手机的姿态[10-12]。考虑到体积、成本和功耗,嵌入智能手机的IMU通常采用MEMS技术制造。智能手机的MEMS IMU测量信息质量低,经典的捷联惯性导航系统(SINS)算法不适用于基于智能手机的行人导航[10-12]。基于行人步行步态的行人航位推算(PDR)算法是一种更可靠的行人定位和导航方法[12]。PDR通过处理传感器量测信息来更新行人位置,而无需接收来自外部的信号,在室内外环境下都可以提供定位信息;换言之,PDR是一个独立的定位系统。然而,由于IMU量测信息复杂的噪声和航向角误差,其位置精度随着行人行走距离的增加而降低。因此,将互补的GNSS和PDR组合在一起是生成更加可靠的行人导航和定位信息的可行方法[12-14]。为提高GNSS/PDR组合导航系统性能,Ye等[15]提出一种GNSS/PDR/Beacon组合导航方法,当GNSS信号较差时,利用Beacon信号和PDR构建组合导航系统,抑制PDR误差。该方法可以有效地提升无GNSS下导航定位精度。Hsu等[16]提出一种3D地图辅助GNSS/PDR组合导航方法,利用3D地图辅助GNSS和PDR组合提高系统在城市复杂环境下的导航和定位精度。该方法可以有效地减轻NLOS信号等对GNSS/PDR组合导航系统精度的影响,通过3D地图辅助可以识别NLOS信号等,提高整个系统在复杂城市环境的定位精度。另外,Rehman等[17]提出一种GNSS/PDR航向联合估计方法,从提高系统航向角精度方面提高整个系统的导航和定位精度。航向角估计是PDR算法的核心,但是该方法并不能解决智能手机和人之间的固定航向偏差带来的定位误差问题。总之,目前GNSS/PDR研究主要是集中在提高步长估计精度、提高步态检测正确率、提高航向角估计精度和改进数据融合方面[17]。目前GNSS/PDR组合主要建立在以卡尔曼滤波为数据融合算法的基础上。在GNSS/PDR组合导航系统中行人轨迹是连续的,充分利用历史信息可以有效地提高行人位置估计精度。
为进一步提高GNSS/PDR组合导航系统性能,本文从数据融合的角度出发,提出一种基于因子图优化(FGO)GNSS/PDR组合导航方法。本文主要研究内容如下:
1) 针对行人导航GNSS或者PDR信息缺失时导航误差快速发散的问题,提出用图论法表示行人位置、GNSS量测信息等之间的相互约束关系的解决方法,基于图的框架还能够支持“即插即用”,为GNSS/PDR融合提供了一个通用并且可灵活配置的框架。
2) 用图优化算法代替常规的卡尔曼滤波算法完成GNSS和PDR的信息融合并估计定位信息。在FGO-GNSS/PDR中,所有过去的状态都作为未知量,所有来自GNSS的位置信息都作为状态的约束,通过最小化整体代价函数获取状态的最优解。相对卡尔曼滤波,FGO-GNSS/PDR方法可以充分利用历史轨迹信息和状态之间的相互联系,提高位置估计精度。
最后本文利用智能手机采集实际场景数据,验证和分析了本文提出算法的有效性。
1 PDR算法
基于智能手机的PDR一种相对定位算法,通过处理手机传感器数据估计行人步长和行走方向更新行人位置[18]。图1为智能手机PDR原理图。图1中,N表示北向,E表示东向,pk和pk+1表示k和k+1时刻的位置向量。假设k时刻行人位置为pk=(xk,yk),航向为θk,从k到k+1时刻步长为SLk,k+1,则k+1时刻位置pk+1=(xk+1,yk+1),更新公式如下:
xk+1=xk+SLk,k+1·cosθk
(1)
yk+1=yk+SLk,k+1·sinθk
(2)

图1 航位推算位置更新原理Fig.1 Principle diagram of position updating
智能手机传感器如加速度计、陀螺仪、磁力计等数据经过处理之后,用来识别行人是否行走,然后估计行人行走的步长。同时利用磁力计和陀螺仪等传感器数据联合估计行人的行走方向,通过上述公式更新位置。图2为基于智能手机的PDR数据处理和原理框图。
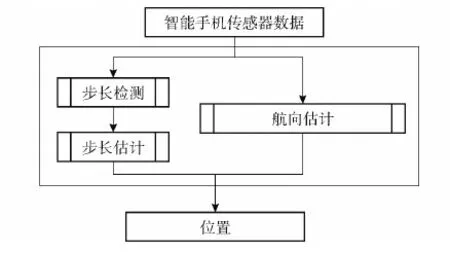
图2 智能手机航位推算原理图Fig.2 Principle diagram of pedestrian positioning based on smartphone function
在智能手机PDR中,通过三轴加速度计的输出检测步长。加速度计输出为时序数据,可以通过检测加速度计峰值和谷值来检测步长。这里采用三轴加速度计的矢量和ak作为输入,计算公式如式(3)所示:
(3)

利用加速度输出估计行人步长计算公式如下:
(4)
式中:α为常值参数,通常取值在0~1之间。
2 GNSS/PDR组合导航
由于传感器噪声和行人航向误差等,PDR结果通常随着时间发散。智能手机GNSS在信号良好的情况下可以提供高精度定位信息,可以构建GNSS和PDR组合导航系统。当GNSS信号良好的情况下通过与PDR组合可以输出稳定的定位信息;当GNSS无法工作时,PDR可以提供定位信息。
2.1 基于卡尔曼滤波PDR/GNSS组合导航方法
PDR/GNSS组合导航方法状态方程以及量测方程如下:
pk+1=Φk,k+1·pk+wk+1
(5)
(6)
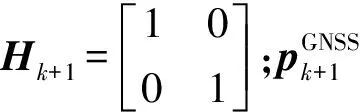
卡尔曼滤波更新过程如下:
(7)
(8)
(9)
(10)
(11)
2.2 基于因子图PDR/GNSS组合导航方法
因子图属于概率图的一种,本质上用图来表示各种变量或者状态之间相互依存关系。因子图最开始用在通信技术中的信道编码估计,经过不断发展,为解决一些复杂的估计问题提供了新的方法和思路。通常,在因子图中会将全局函数经过分解成多个局部函数的乘积,这样可以明显地减少全局函数求解的复杂度。在导航系统的应用中,因子图本质上表示并可视化了导航系统中的状态和量测信息之间的联系。
因子图由变量节点和状态节点组成,并通过无向边连接。假设函数g(X1,X2,…,Xn)可以分解为如下形式:
(12)
式中:f(Sj)表示为局部函数,Sj为状态变量X的集合。为方便表示,假设g(X1,X2,…,Xn)有4个变量,式(12)可以表示为如下乘积关系:
g(X1,X2,X3,X4)=f(X1)f(X2,X4)f(X1,X3)f(X1,X3,X4)
(13)
以上乘积关系可以用图3所示因子图表示,其中黑色方框表示因子节点,圆形代表变量节点。上述过程表示了经过因子图模型将复杂函数分解为 4个局部函数乘积。
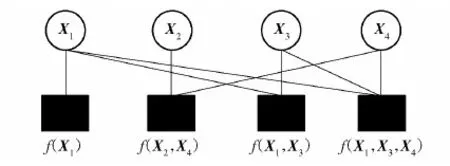
图3 局部函数分解因子图Fig.3 Factor graph of local function decomposition
假设一组变量(x1,…,xn)的联合概率密度函数为f(x1,…,xn),变量之间概率关系可以写成如下形式:
(14)
为方便描述,假设n=4,则式(14)可以写成如下形式:
f(x1,…,x4)=f(x1)f(x2|x1)f(x3|x1,x2)f(x4|x1,x2,x3)
(15)
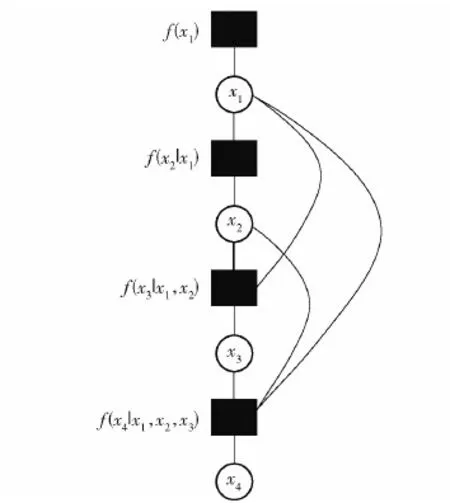
图4 变量依存关系因子图Fig.4 Factor graph of variable dependency relation
进一步地,以上关系可以用图4所示因子图表示。 通过2.1节中卡尔曼滤波状态估计和更新公式可以看出,卡尔曼滤波采用递推的方式估计和更新状态估计。通过状态转移模型和量测模型可以知道,状态之间通过状态转移方程相互联系,状态和量测信息之间通过量测观测方程相互联系。结合上面的因子图描述和GNSS/PDR组合导航状态和量测模型,可以利用因子图表示GNSS/PDR组合导航的状态转移和量测信息之间的概率关系。根据贝叶斯概率准则,式(5)和式(6)中的状态和量测信息的之间概率依存关系如下公式:
(16)
式中:变量p0∶k全局条件概率密度函数与等式右边的似然概率密度和状态转移先验概率的乘积呈正比。具体如下:
(17)
因此,状态的最优估计可以转换为求取状态变量的最大后验概率(MAP),可以表示为
(18)
假设噪声服从高斯分布,概率密度函数P(pi|zi)可以写为
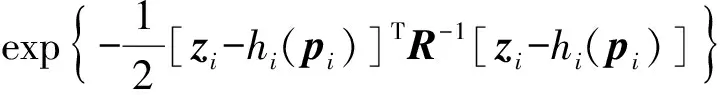
(19)
要获得最大后验概率估计,需要将下面公式最小化:
[zi-hi(pi)]TR-1[zi-hi(pi)]
(20)
根据式(16)描述的概率依存关系,采用因子图描述和表示GNSS/PDR组合导航中的状态和量测信息之间的关系。GNSS/PDR组合导航因子图如图5所示,GNSS因子和PDR因子共同作为状态的约束信息。结合式(21)和GNSS/PDR组合导航模型,状态的最优估计可以转化成为求取下面代价函数的最小值。
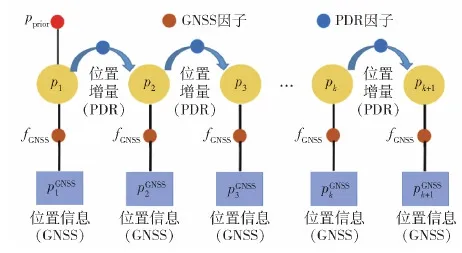
图5 FGO-GNSS/PDR组合导航方法Fig.5 FGO-GNSS/PDR integrated navigation method
状态代价函数如下:
(21)
量测代价函数如下:
(22)
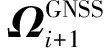
总的代价函数如下:
(23)
在卡尔曼滤波中,估计pk+1时默认pk是已知的,事实上pk是存在误差的并且会对状态估计产生影响。根据以上分析,状态之间是相互联系的。将过去所有的状态都作为未知量,并结合根据式(16)和式(17),可以得到新的代价函数如下:
(24)
可以通过列克夸尔文算法或者高斯牛顿法等求取式(24)代价函数最小值,并获得状态的最优估计。
2.3 因子图求解
构建代价函数之后,状态的最优估计可以从求取代价函数的最小值获取。结合式(18)~式(20),式(21)和式(22)[19-21]可以写为
(25)
(26)
整体代价函数可以写为
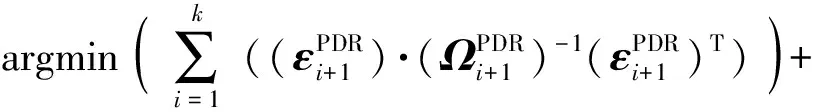
(27)
为方便描述式(27)中代价函数最小值的求取过程,代价函数[19-21]可以写成如下通用形式:
(28)
式中:ei(X)为误差代价函数;Ω为对应误差方差矩阵的逆矩阵。
(29)
式(27)可以展开为
(30)
综上,可得以下公式:

(31)
将上述公式对ΔX进行求导,并令求导后的公式值为0,则可得以下公式:
aΔX=-b
(32)
为稳定的求得ΔX,通常引入参数λ,新的公式如下:
(a+λI)ΔX=-b
(33)
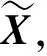
(34)
将上述过程进行不停循环,直至达到设定的循环次数,或者误差小于设置的值。图6为求解过程流程图。
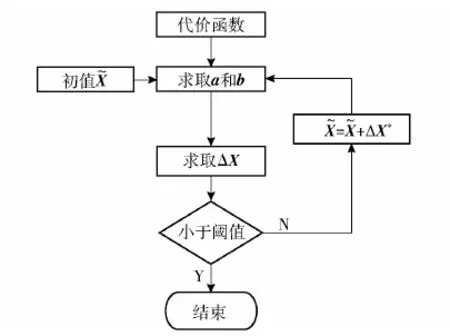
图6 求解过程流程图Fig.6 Flow chart of the solving process
3 实验结果与分析
为验证本文提出算法的性能,采集智能手机实际场景数据进行实验。通过处理实际场景数据,更有效地测试和评价本文提出的算法。实验采用华为Mate 40 Pro手机和安卓APP采集手机传感器数据进行处理。采集的数据包括带时标的GNSS位置、三轴加速度计、三轴陀螺仪、三轴磁传感器数据等。
为进一步进行数据对比,实验中采用GNSS RTK数据作为轨迹基准计算位置误差,实验场景如图7所示。GNSS RTK高精度定位系统是一种基于卫星导航定位地基增强系统的高性能GNSS RTK接收机,包含GNSS接收机、GNSS双天线、锂电池电源等,通过4G通道利用千寻服务作为差分修正数据的输入源。GNSS RTK系统定位精度可达厘米级,可作为行人导航的位置基准。

图7 数据采集装置Fig.7 Dataset collecting equipment
实验中PDR使用的航向角为手机加速度计、陀螺仪和磁传感器融合后的结果。采用两种不同的方式携带手机采集实验数据:第1种是模拟行人行走看手机的情形,因此将手机持于胸前;第2种模拟行人手机放置在背包中,将手机固定在测试背带上。
3.1 手持实验
首先进行手持智能手机导航实验,将手机持于胸前模仿行人边走路边看手机的场景。行人边走边采集数据,同时背包中的GNSS RTK输出的数据被笔记本电脑采集作为后续的手机定位误差计算基准。手机加速度计能够感受到行人行走带来的加速度计测量值的变化。实验数据处理时,首先处理加速度数据,检测行人步态并估计行人步长,然后根据对应的加速度时标和GNSS信息时间同步,获取对应的GNSS位置信息进行融合。

图8 手持实验1水平位置误差和分布Fig.8 Hand-held experimental 1 horizontal position errors and distribution
图8为实验中水平位置误差结果,图8(a)为水平定位误差与步数的关系,图8(b)为水平位置误差统计分布。从图8中可以看出,FGO-GNSS/PDR具有更好的定位精度。表1给出了两种方法的水平误差统计结果对比。由表1可知,与KF-GNSS/PDR相比,FGO-GNSS/PDR水平位置误差平均值下降了43.9%,误差均方根值下降了35.1%。另一组实验结果如图9所示,类似地,FGO-GNSS/PDR获得了更好的定位结果。表2为对应的统计结果分析,水平位置误差均值下降了43.8%,误差均方根下降了48.3%。
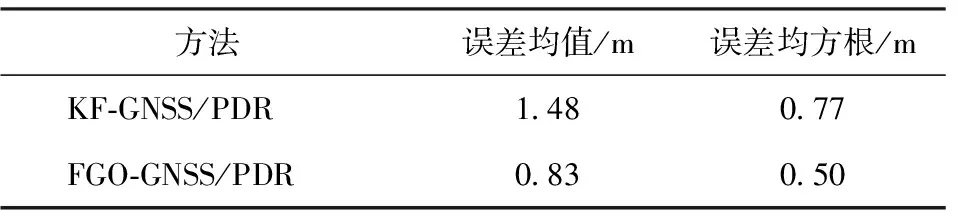
表1 手持实验1水平位置误差统计结果Table 1 Hand-held experiment 1 statistical results of horizontal position errors
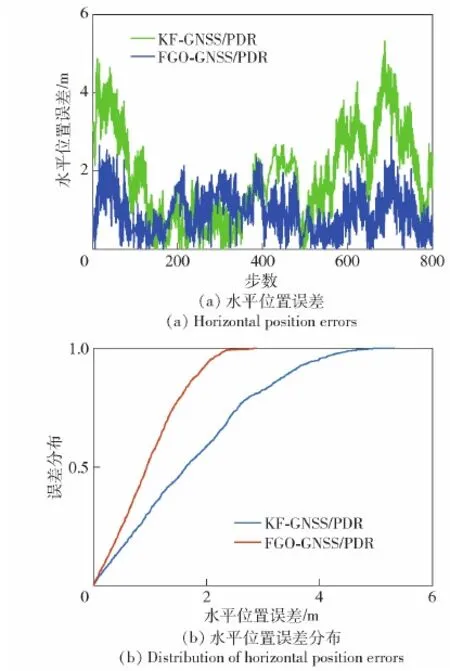
图9 手持实验2水平位置误差和分布Fig.9 Hand-held experiment 2 horizontal position errors and distribution

表2 手持实验2水平位置误差统计结果
3.2 背包实验
除手持实验之外,进行两组将手机放置在背包中的实验,手机水平放置,以保证手机的航向和行人航向尽可能一致。同样对水平定位结果进行分析,两组实验水平位置误差分别如图10和图11所示。图10(a)和图11(a)分别为水平定位误差和步数之间的关系;图10(b)和图11(b)分别为对应的水平定位误差的统计结果和分布图。与KF-GNSS/PDR方法相比,FGO-GNSS/PDR方法同样地获得了更好的定位精度。表3和表4给出了进一步对应的统计分析结果:第1组数据中,水平位置平均误差减少了40.5%,误差均方根降低了36.9%;第2组数据中,水平位置平均误差减少了56.0%,误差均方根降低了48.9%。
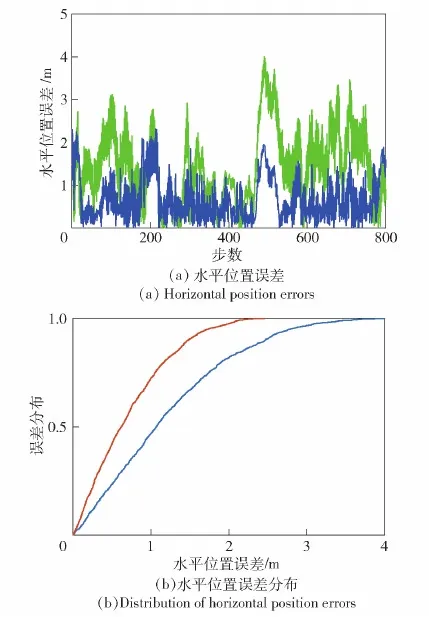
图10 背包实验1水平位置误差和分布Fig.10 Knapsack experiment 1 horizontal position errors and distribution

图11 背包实验2水平位置误差和分布Fig.11 Knapsack experiment 2 horizontal position errors and distribution
3.3 结果分析、讨论和展望
手持和背包实验中通过与卡尔曼滤波算法的对比,误差统计分析结果表明相对于卡尔曼滤波,本文提出的FGO-GNSS/PDR方法能够有效地提升GNSS/PDR定位精度,GNSS/PDR方法平均定位误差和定位误差均方根值都得到了不同的降低。实验中尽量保持了手机航向角和行人行走方向的一致性,以排除手机航向角和行人之间的误差对结果的影响。另外,实验中KF-GNSS/PDR和FGO-GNSS/PDR方法的噪声协方差矩阵设置值保持一致,以保证对比的公平性。实验结果可以很好地证明基于历史轨迹的整体优化方法能够有效地降低定位误差。

表3 背包实验1水平位置误差统计结果Table 3 Knapsack experiment 1 statistical results of horizontal position errors
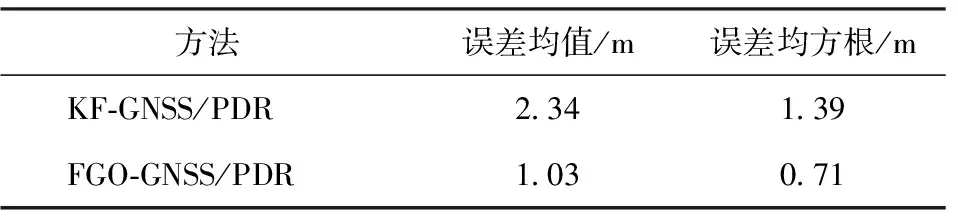
表4 背包实验2水平位置误差统计结果Table 4 Knapsack experiment 2 statistical results of horizontal position errors
虽然本文基于因子图GNSS/PDR融合算法能够在同样条件下比卡尔曼滤波获得更好的定位精度,以下4点仍然值得继续深入研究:
1) 本文中没有考虑GNSS提供的速度,实际速度可以用来修正航向角,可以进一步考虑基于位置和速度建立新的模型。
2) GNSS位置信息在城市峡谷等环境存在一些较大的误差,例如NLOS信号误差、多路径信号误差等,基于因子图研究完好性检测算法有助于提升系统的鲁棒性和整体性能。
3) 基于手机的PDR的难点在于手机的放置方式随意性和多变性,有时并不能获取稳定的航向角;例如手机竖直放置在口袋中,但是此时加速度数据仍然可以用来检测步数用来辅助GNSS位置估计。
4) 本文基于因子图的GNSS/PDR组合导航可以进一步拓展成多源信息融合导航系统,进一步开发室内外无缝导航系统。
4 结论
本文提出一种基于FGO-GNSS/PDR组合导航方法,采用因子图算法代替卡尔曼滤波进行融合,并通过实际场景实验中证明了本文方法能够提高系统的定位精度。得出主要结论如下:
1) 与卡尔曼滤波算法相比,因子图算法可以进一步降低系统平均定位误差超过40%。因为使用了较多的历史数据,计算量偏大,但更高的定位精度使之可应用于行人及单兵导航装置。
2) 与卡尔曼滤波相比,因子图算法能够充分利用历史信息,通过整体优化能够有效地提高GNSS/PDR组合导航系统的定位精度。
3) 图优化算法中,求解代价函数的迭代过程有助于提高非线性模型下的估计精度。
